人教版高中物理选择性必修第二册第一章安培力与洛伦兹力专题课二带电粒子在有界匀强磁场中的运动课件(26页ppt)
文档属性
| 名称 | 人教版高中物理选择性必修第二册第一章安培力与洛伦兹力专题课二带电粒子在有界匀强磁场中的运动课件(26页ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-19 07:37:46 | ||
图片预览






文档简介
(共26张PPT)
第一章 安培力与洛伦兹力
专题课二 带电粒子在有界匀强磁场中的运动
第*页
专题一 带电粒子在有界匀强磁场中的运动
要点 归纳
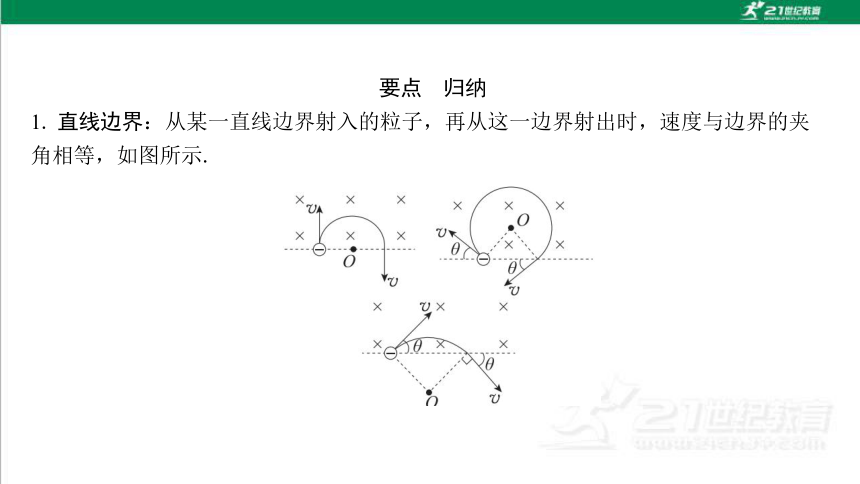
1. 直线边界:从某一直线边界射入的粒子,再从这一边界射出时,速度与边界的夹 角相等,如图所示.
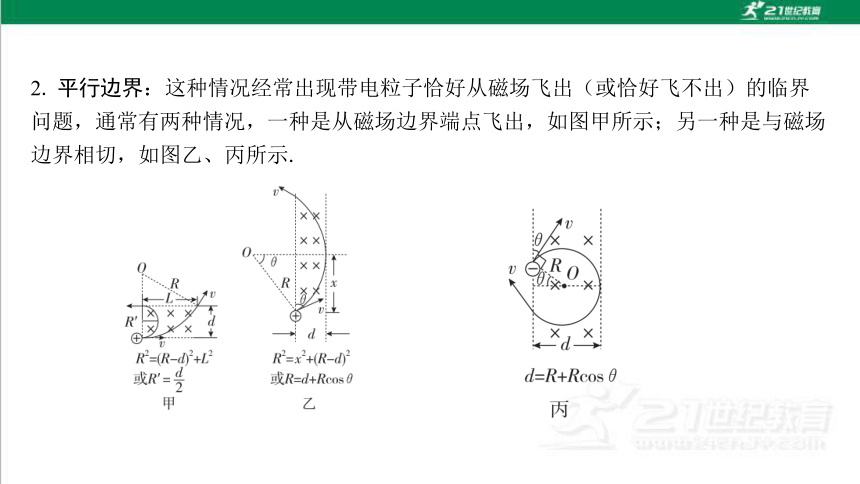
2. 平行边界:这种情况经常出现带电粒子恰好从磁场飞出(或恰好飞不出)的临界 问题,通常有两种情况,一种是从磁场边界端点飞出,如图甲所示;另一种是与磁场 边界相切,如图乙、丙所示.
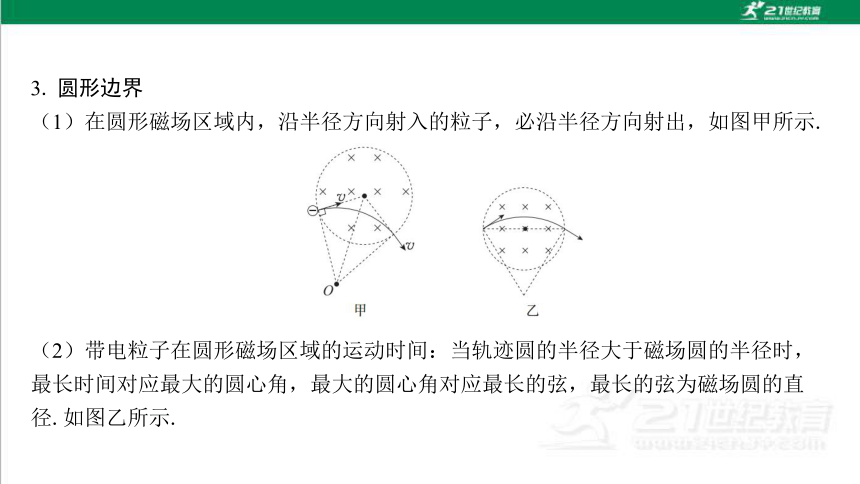
3. 圆形边界
(1)在圆形磁场区域内,沿半径方向射入的粒子,必沿半径方向射出,如图甲所示.
(2)带电粒子在圆形磁场区域的运动时间:当轨迹圆的半径大于磁场圆的半径时, 最长时间对应最大的圆心角,最大的圆心角对应最长的弦,最长的弦为磁场圆的直 径.如图乙所示.
研习 经典
B
解析:电子从a点射出,运动轨迹如图线①,
名师点评
解决此类问题首先要准确地画出粒子运动的轨迹,找到圆心,利用几何关系求出 半径,必要时用圆规辅助,准确作图能起到事半功倍的效果.
针对 训练
A. 粒子的运动轨迹可能通过圆心O
B. 最少经2次碰撞,粒子就可能从小孔射出
C. 射入小孔时粒子的速度越大,在圆内运动时间越短
D. 每次碰撞后瞬间,粒子速度方向一定平行于碰撞点与圆心O的连线
BD
解析:假设粒子带负电,第一次从A点和筒壁发生碰撞如图,O1为圆周运动的圆心,
由几何关系可知∠O1AO为直角,即粒子此时的速度方向为OA,说明粒子在和筒壁
碰撞时速度会反向,由圆的对称性,在其他点撞击同理,D正确;假设粒子运动过程
过O点,则过P点的速度的垂线和OP连线的中垂线是平行的,不能交于一点确定圆心,由圆形对称性,撞击筒壁以后的A点的速度垂线和AO连线的中垂线依旧平行,不能确定圆心,则粒子不可能过O点,A错误;由题意可知粒子射出磁场以后的圆心组成的多边形应为以筒壁为内接圆的多边形,最少应为三角形如图所示
即撞击两次,B正确;速度越大,粒子做圆周运动的半径越大,碰撞次数可能会增 多,粒子运动时间不一定减少,C错误.故选BD.
第*页
专题二 带电粒子在有界磁场中运动的临界问题
要点 归纳
解决带电粒子在有界匀强磁场中运动的临界问题的关键,通常以题目中的“恰 好”“最大”“至少”等为突破口,寻找临界点,确定临界状态,根据匀强磁场边界 和题设条件画好轨迹,建立几何关系求解.
(1)刚好穿出或刚好不能穿出匀强磁场的条件是带电粒子在匀强磁场中运动的轨迹 与边界相切.
(2)当以一定的速率垂直射入匀强磁场时,运动的弧长越长、圆心角越大,则带电 粒子在有界匀强磁场中的运动时间越长.
(3)比荷相同的带电粒子以不同的速率v进入磁场时,圆心角越大的,运动时 间越长.
研习 经典
BD
名师点评
由于电荷的电性不同、离开磁场的边界不同、速度方向不同,会造成多解,所以 解决此类问题时,一定要考虑全面,不要漏解.
针对 训练
AB
第*页
课后提素养 深刻剖析 提升能力
A. 0.5 m B. 1.2 m
C. 1.6 m D. 2.0 m
B
1
2
3
4
解析:由题意作出带电粒子的圆心及轨迹,如图所示
由洛伦兹力提供向心力,
由几何关系得L=rsin α=1.2 m,故选B.
1
2
3
4
A. 2BkL
BD
1
2
3
4
1
2
3
4
A. 通过的路程一定越小
B. 运动的角速度一定越小
C. 运动的轨道半径一定越大
D. 运动的周期一定越小
C
1
2
3
4
1
2
3
4
4. 如图所示,直角坐标系中y轴右侧存在一垂直纸面向里、宽为a的有界匀强磁场,磁感应强度为B,右边界PQ平行于y轴,一粒子(重力不计)从原点O以与x轴正方向成θ角的速率v垂直射入磁场,当斜向上射入时,粒子恰好垂直PQ射出磁场,当斜向下射入时,粒子恰好不从右边界射出,求:
(1)粒子的比荷;
1
2
3
4
(2)粒子恰好不从右边界射出时在磁场中运动的时间.
1
2
3
4
第一章 安培力与洛伦兹力
专题课二 带电粒子在有界匀强磁场中的运动
第*页
专题一 带电粒子在有界匀强磁场中的运动
要点 归纳
1. 直线边界:从某一直线边界射入的粒子,再从这一边界射出时,速度与边界的夹 角相等,如图所示.
2. 平行边界:这种情况经常出现带电粒子恰好从磁场飞出(或恰好飞不出)的临界 问题,通常有两种情况,一种是从磁场边界端点飞出,如图甲所示;另一种是与磁场 边界相切,如图乙、丙所示.
3. 圆形边界
(1)在圆形磁场区域内,沿半径方向射入的粒子,必沿半径方向射出,如图甲所示.
(2)带电粒子在圆形磁场区域的运动时间:当轨迹圆的半径大于磁场圆的半径时, 最长时间对应最大的圆心角,最大的圆心角对应最长的弦,最长的弦为磁场圆的直 径.如图乙所示.
研习 经典
B
解析:电子从a点射出,运动轨迹如图线①,
名师点评
解决此类问题首先要准确地画出粒子运动的轨迹,找到圆心,利用几何关系求出 半径,必要时用圆规辅助,准确作图能起到事半功倍的效果.
针对 训练
A. 粒子的运动轨迹可能通过圆心O
B. 最少经2次碰撞,粒子就可能从小孔射出
C. 射入小孔时粒子的速度越大,在圆内运动时间越短
D. 每次碰撞后瞬间,粒子速度方向一定平行于碰撞点与圆心O的连线
BD
解析:假设粒子带负电,第一次从A点和筒壁发生碰撞如图,O1为圆周运动的圆心,
由几何关系可知∠O1AO为直角,即粒子此时的速度方向为OA,说明粒子在和筒壁
碰撞时速度会反向,由圆的对称性,在其他点撞击同理,D正确;假设粒子运动过程
过O点,则过P点的速度的垂线和OP连线的中垂线是平行的,不能交于一点确定圆心,由圆形对称性,撞击筒壁以后的A点的速度垂线和AO连线的中垂线依旧平行,不能确定圆心,则粒子不可能过O点,A错误;由题意可知粒子射出磁场以后的圆心组成的多边形应为以筒壁为内接圆的多边形,最少应为三角形如图所示
即撞击两次,B正确;速度越大,粒子做圆周运动的半径越大,碰撞次数可能会增 多,粒子运动时间不一定减少,C错误.故选BD.
第*页
专题二 带电粒子在有界磁场中运动的临界问题
要点 归纳
解决带电粒子在有界匀强磁场中运动的临界问题的关键,通常以题目中的“恰 好”“最大”“至少”等为突破口,寻找临界点,确定临界状态,根据匀强磁场边界 和题设条件画好轨迹,建立几何关系求解.
(1)刚好穿出或刚好不能穿出匀强磁场的条件是带电粒子在匀强磁场中运动的轨迹 与边界相切.
(2)当以一定的速率垂直射入匀强磁场时,运动的弧长越长、圆心角越大,则带电 粒子在有界匀强磁场中的运动时间越长.
(3)比荷相同的带电粒子以不同的速率v进入磁场时,圆心角越大的,运动时 间越长.
研习 经典
BD
名师点评
由于电荷的电性不同、离开磁场的边界不同、速度方向不同,会造成多解,所以 解决此类问题时,一定要考虑全面,不要漏解.
针对 训练
AB
第*页
课后提素养 深刻剖析 提升能力
A. 0.5 m B. 1.2 m
C. 1.6 m D. 2.0 m
B
1
2
3
4
解析:由题意作出带电粒子的圆心及轨迹,如图所示
由洛伦兹力提供向心力,
由几何关系得L=rsin α=1.2 m,故选B.
1
2
3
4
A. 2BkL
BD
1
2
3
4
1
2
3
4
A. 通过的路程一定越小
B. 运动的角速度一定越小
C. 运动的轨道半径一定越大
D. 运动的周期一定越小
C
1
2
3
4
1
2
3
4
4. 如图所示,直角坐标系中y轴右侧存在一垂直纸面向里、宽为a的有界匀强磁场,磁感应强度为B,右边界PQ平行于y轴,一粒子(重力不计)从原点O以与x轴正方向成θ角的速率v垂直射入磁场,当斜向上射入时,粒子恰好垂直PQ射出磁场,当斜向下射入时,粒子恰好不从右边界射出,求:
(1)粒子的比荷;
1
2
3
4
(2)粒子恰好不从右边界射出时在磁场中运动的时间.
1
2
3
4
