人教版高中物理选择性必修第二册第一章安培力与洛伦兹力3带电粒子在匀强磁场中的运动课件(71页ppt)
文档属性
| 名称 | 人教版高中物理选择性必修第二册第一章安培力与洛伦兹力3带电粒子在匀强磁场中的运动课件(71页ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-19 08:04:01 | ||
图片预览











文档简介
(共71张PPT)
第一章 安培力与洛伦兹力
3.带电粒子在匀强磁场中的运动
核心素养:
1. 运用所学知识,能够解释带电粒子在匀强磁场中的运动.(物理观念)
2. 通过理论分析掌握带电粒子在匀强磁场中做匀速圆周运动的半径、周期、圆心角 等物理量.(科学思维)
3. 探究带电粒子在匀强磁场中的匀速圆周运动的半径、周期与哪些物理量有关.(科 学探究)
4. 通过先实验探究,再理论分析与推导的顺序,既有丰富的感性材料,又有清晰的 理论依据,在理论与实践结合的过程中体会成功的喜悦.(科学态度与责任)
第*页
研习任务一 带电粒子在匀强磁场中运动规律
合作 讨论
1. 你还记得物体做匀速圆周运动的条件吗?试着总结一下.
提示:①物体要受到一个始终与运动方向垂直的向心力作用;②向心力与物体的运动 方向在同一个平面内;③向心力与物体的运动方向垂直,不做功,不改变物体速度的 大小.
2. 如果沿着与磁场垂直的方向发射带电粒子,带电粒子受到的洛伦兹力的方向怎 样?洛伦兹力与带电粒子的运动方向是否处于同一平面内?带电粒子做什么运动?
提示:如图所示,洛伦兹力垂直速度方向,也垂直磁场方向,洛伦 兹力与粒子的运动方向在同一平面内,带电粒子在这个平面内做匀 速圆周运动.
教材 认知
1. 带电粒子在匀强磁场中的运动
(1)若v∥B,带电粒子以速度v做匀速直线运动,其所受洛伦兹力F=0.
(2)若v⊥B,此时初速度方向、洛伦兹力的方向均与磁场方向 ,粒子在垂 直于 方向的平面内运动.
①洛伦兹力与粒子的运动方向 ,只改变粒子速度的 ,不改变粒子速 度的 .
②带电粒子在垂直于磁场的平面内做 运动, 提供向心力.
垂直
磁场
垂直
方向
大小
匀速圆周
洛伦兹力
无关
要点 归纳
1. 带电粒子在磁场中做匀速圆周运动的半径公式
2. 带电粒子在磁场中做匀速圆周运动的周期公式
研习 经典
A. T增大 B. T减小
C. R增大 D. R减小
D
名师点评
做这类题目时一定要牢记半径公式和周期公式,看清楚带电粒子的质量和电荷 量,善用控制变量法,抓住不变量判断变化量,必要时把相关公式写在题目空白处.
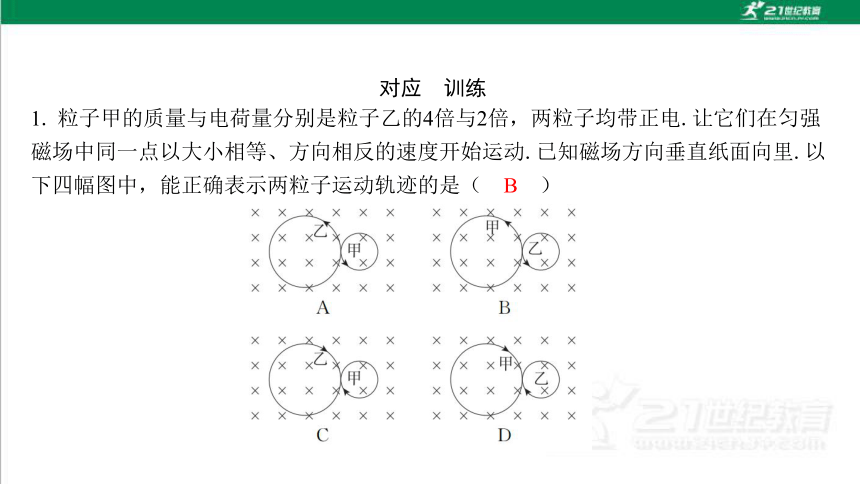
对应 训练
B
第*页
研习任务二 观察带电粒子的运动径迹
合作 讨论
如图所示,可用洛伦兹力演示仪观察运动电子
在匀强磁场中的偏转.
(1)不加磁场时,电子束的运动轨迹如何?加上磁场时,电子束的运动轨迹如何?
提示:(1)不加磁场时电子束的轨迹为一条直线,加磁场后电子束的径迹是一个圆.
(2)如果保持出射电子的速度不变,增大磁感应强度,轨迹圆半径如何变化?如果 保持磁感应强度不变,增大出射电子的速度,圆半径如何变化?
提示:(2)当电子束出射速度不变,磁感应强度变大时,这个圆的半径变小;当磁 感应强度不变,电子束出射速度变大时,这个圆的半径变大.
要点 归纳
1. 洛伦兹力演示仪的构造
(1)电子枪:可以发射电子束.
(2)玻璃泡:内部充有稀薄的气体,在电子束通过时能够显示电子的径迹.
(3)励磁线圈:能够在两个线圈之间产生匀强磁场,磁场的方向与两个线圈中心的 连线平行.
2. 实验现象
(1)不加磁场时,电子束的径迹是一条直线(图甲).加磁场后电子束的径迹是一个 圆(图乙).
(2)当电子束出射速度不变,磁感应强度变大时,这个圆的半径变小.
(3)当磁感应强度不变,电子束出射速度变大时,这个圆的半径变大.
3. 实验结论
带电粒子以垂直磁场的方向射入,在磁场中做匀速圆周运动,其运动规律与理论推导 相吻合.
研习 经典
A. 甲图中的电子束不受洛伦兹力
B. 乙图中的电子束不受洛伦兹力
C. 甲图中的电子束处在垂直纸面的磁场中
D. 乙图中的电子束处在平行纸面的磁场中
A
解析:甲图中的电子束的轨迹没有偏转,说明不受洛伦兹力,故A正确;乙图中的电 子束的轨迹发生偏转,说明受洛伦兹力,故B错误;甲图中的电子束的轨迹没有偏 转,说明不受洛伦兹力,电子束处在平行纸面的磁场中或处于磁感应强度为零的位 置,故C错误;乙图中的电子束的轨迹是圆周,说明受洛伦兹力,电子束处在垂直纸 面的磁场中,故D错误.
名师点评
解决此类问题时一定要清楚洛伦兹力演示仪的构造,洛伦兹力演示仪的两个励磁 线圈会产生垂直纸面的磁场,只要明确电子束的运动轨迹就可以确定电子束是否偏 转,是否受力.
对应 训练
B
A. 励磁线圈通以逆时针方向的电流,则能形成结构示意图中的电子运动径迹
B. 励磁线圈通以顺时针方向的电流,则能形成结构示意图中的电子运动径迹
C. 保持励磁电压不变,增加加速电压,电子束形成圆周的半径减小
D. 保持加速电压不变,增加励磁电压,电子束形成圆周的半径增大
第*页
研习任务三 带电粒子在匀强磁场中的圆周运动
合作 讨论
我们知道,在几何中,只要确定了一个圆的圆心和半径,这个圆就唯一确定了.带电 粒子在匀强磁场中做圆周运动,我们应该如何确定粒子运动的轨迹呢?
提示:要想确定粒子的运动轨迹,需要确定粒子做圆周运动的圆心和半径.圆心在入 射速度的垂线、出射速度的垂线和轨迹弦的垂直平分线上,以上三条线中任意两条线 的交点就是轨迹的圆心.粒子做圆周运动的半径可以根据几何关系或半径公式求解.
要点 归纳
在研究带电粒子在匀强磁场中做匀速圆周运动问题时,可以按照“找圆心,求半径, 求角度,解未知”的思路进行.
1. 找圆心——两线定一“心”
(1)圆心一定在垂直于速度的直线上.
如图甲所示,已知入射点P(或出射点M)的速度方向,可通过入射点和出射点作速 度的垂线,两条直线的交点就是圆心.
(2)圆心一定在弦的中垂线上.
如图乙所示,作P、M连线的中垂线,
与任一速度的垂线的交点为圆心.
(2)根据几何知识求解,如图所示.
3. 求角度
如图所示,
(1)带电粒子射出磁场的速度方向与射入磁场的速度方向之间的夹角φ叫作偏向角, 偏向角等于圆弧AB对应的圆心角α,即α=φ.
(2)圆弧AB所对应圆心角α等于弦AB与切线的夹角(弦切角)θ的2倍,即α=2θ.
(3)相对的弦切角相等;相邻的弦切角互补,即θ+θ'=180°.
(4)进出同一直边界时速度方向与该边界的夹角相等,如图所示.
研习 经典
B
名师点评
在解决此类问题时要熟悉“找圆心,求半径,解未知”三步曲,这三步要根据具 体情况来灵活使用,不一定每步都用到,也不一定有严格的先后顺序.
对应 训练
C. 2∶1
B
知识 构建
第*页
课后提素养 深刻剖析 提升能力
基础 题组
1. 判断正误.
√
×
×
×
×
×
A. 1∶1∶2 B. 1∶3∶4
C. 1∶1∶1
D
A. 若速率相等,则半径必相等
B. 若质量相等,则周期必相等
C. 若动量大小相等,则半径必相等
D. 若动能相等,则周期必相等
BC
中档 题组
A. 运动轨迹的半径是Ⅰ中的k倍
B. 加速度的大小是Ⅰ中的k倍
C. 做圆周运动的周期是Ⅰ中的k倍
D. 做圆周运动的角速度与Ⅰ中的相等
AC
A
3. 如图所示,一个质量为m、带负电荷、电荷量为q、不计重力的
带电粒子从x轴上的P点以速度v沿与x轴成60°的方向射入第一象限
内的匀强磁场中,并恰好垂直于y轴射出第一象限.已知OP=a,求:
(1)匀强磁场的磁感应强度B的大小;
(2)带电粒子穿过第一象限所用的时间.
第*页
课时作业(三)
[基础训练]
A. 它所受的洛伦兹力是恒定不变的
B. 它的速度是恒定不变的
C. 它的速度与磁感应强度B成正比
D. 它的运动周期与速度的大小无关
D
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
A. 1∶2,1∶2 B. 2∶1,2∶1
C. 2∶1,1∶2 D. 1∶2,2∶1
C
1
2
3
4
5
6
7
8
9
10
11
12
D
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
A. 1∶2 B. 2∶1
D. 1∶1
B
1
2
3
4
5
6
7
8
9
10
11
12
解析:画出正、负电子在磁场中运动的轨迹如图所示:
1
2
3
4
5
6
7
8
9
10
11
12
B
1
2
3
4
5
6
7
8
9
10
11
12
解析:根据题意作出正电荷运动的轨迹如图所示:
1
2
3
4
5
6
7
8
9
10
11
12
A. 粒子带正电,从B点射入
B. 粒子带负电,从B点射入
C. 粒子带正电,从A点射入
D. 粒子带负电,从A点射入
B
1
2
3
4
5
6
7
8
9
10
11
12
A. 粒子带正电
C. 粒子做圆周运动的半径为L
D
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
8. 一个带电荷量为+q,质量为m的粒子在磁感应强度为B的匀强磁场中以初速度v0垂 直于磁场自A点开始运动,如图所示,经时间t,粒子到达C点,求:
(1)画出粒子轨迹示意图;
答案:(1)见解析图
解析:(1)轨迹示意图如图所示
1
2
3
4
5
6
7
8
9
10
11
12
(2)粒子在磁场中运动的周期和加速度大小a;
1
2
3
4
5
6
7
8
9
10
11
12
(3)连接AC与v0所在直线间的夹角θ.
1
2
3
4
5
6
7
8
9
10
11
12
[能力提升]
A. 两个电子在磁场中运动的轨迹半径一定相同
B. 两个电子在磁场中运动的时间有可能相同
C. 进入圆形区域的电子一定先飞离磁场
D. 进入圆形区域的电子一定不会后飞离磁场
ABD
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
A. 电子将向右偏转
B. 电子打在MN上的点与O'点的距离为d
D
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
A. a、b两带电粒子的运动轨迹半径之比为1∶2
B. a、b两带电粒子的速度大小之比为2∶3
C. a、b两带电粒子的质量之比为2∶3
D. a、b两带电粒子的比荷之比为2∶3
AC
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
12. 在如图所示的平面直角坐标系Oxy中,有一个圆形区域的匀强磁场(图中未画 出),磁场方向垂直于Oxy平面,坐标原点为该圆形磁场区域的圆心.现有一质量为 m,带电荷量为+q的带电粒子(重力不计)从O点开始以初速度v沿x轴正方向进入磁 场,粒子经过y轴上P点时速度方向与y轴正方向夹角为θ=30°,已知OP=L,求:
(1)磁感应强度的大小;
1
2
3
4
5
6
7
8
9
10
11
12
解析:(1)依题意,粒子运动轨迹如图所示
1
2
3
4
5
6
7
8
9
10
11
12
(2)该圆形磁场区域的面积.
1
2
3
4
5
6
7
8
9
10
11
12
第一章 安培力与洛伦兹力
3.带电粒子在匀强磁场中的运动
核心素养:
1. 运用所学知识,能够解释带电粒子在匀强磁场中的运动.(物理观念)
2. 通过理论分析掌握带电粒子在匀强磁场中做匀速圆周运动的半径、周期、圆心角 等物理量.(科学思维)
3. 探究带电粒子在匀强磁场中的匀速圆周运动的半径、周期与哪些物理量有关.(科 学探究)
4. 通过先实验探究,再理论分析与推导的顺序,既有丰富的感性材料,又有清晰的 理论依据,在理论与实践结合的过程中体会成功的喜悦.(科学态度与责任)
第*页
研习任务一 带电粒子在匀强磁场中运动规律
合作 讨论
1. 你还记得物体做匀速圆周运动的条件吗?试着总结一下.
提示:①物体要受到一个始终与运动方向垂直的向心力作用;②向心力与物体的运动 方向在同一个平面内;③向心力与物体的运动方向垂直,不做功,不改变物体速度的 大小.
2. 如果沿着与磁场垂直的方向发射带电粒子,带电粒子受到的洛伦兹力的方向怎 样?洛伦兹力与带电粒子的运动方向是否处于同一平面内?带电粒子做什么运动?
提示:如图所示,洛伦兹力垂直速度方向,也垂直磁场方向,洛伦 兹力与粒子的运动方向在同一平面内,带电粒子在这个平面内做匀 速圆周运动.
教材 认知
1. 带电粒子在匀强磁场中的运动
(1)若v∥B,带电粒子以速度v做匀速直线运动,其所受洛伦兹力F=0.
(2)若v⊥B,此时初速度方向、洛伦兹力的方向均与磁场方向 ,粒子在垂 直于 方向的平面内运动.
①洛伦兹力与粒子的运动方向 ,只改变粒子速度的 ,不改变粒子速 度的 .
②带电粒子在垂直于磁场的平面内做 运动, 提供向心力.
垂直
磁场
垂直
方向
大小
匀速圆周
洛伦兹力
无关
要点 归纳
1. 带电粒子在磁场中做匀速圆周运动的半径公式
2. 带电粒子在磁场中做匀速圆周运动的周期公式
研习 经典
A. T增大 B. T减小
C. R增大 D. R减小
D
名师点评
做这类题目时一定要牢记半径公式和周期公式,看清楚带电粒子的质量和电荷 量,善用控制变量法,抓住不变量判断变化量,必要时把相关公式写在题目空白处.
对应 训练
B
第*页
研习任务二 观察带电粒子的运动径迹
合作 讨论
如图所示,可用洛伦兹力演示仪观察运动电子
在匀强磁场中的偏转.
(1)不加磁场时,电子束的运动轨迹如何?加上磁场时,电子束的运动轨迹如何?
提示:(1)不加磁场时电子束的轨迹为一条直线,加磁场后电子束的径迹是一个圆.
(2)如果保持出射电子的速度不变,增大磁感应强度,轨迹圆半径如何变化?如果 保持磁感应强度不变,增大出射电子的速度,圆半径如何变化?
提示:(2)当电子束出射速度不变,磁感应强度变大时,这个圆的半径变小;当磁 感应强度不变,电子束出射速度变大时,这个圆的半径变大.
要点 归纳
1. 洛伦兹力演示仪的构造
(1)电子枪:可以发射电子束.
(2)玻璃泡:内部充有稀薄的气体,在电子束通过时能够显示电子的径迹.
(3)励磁线圈:能够在两个线圈之间产生匀强磁场,磁场的方向与两个线圈中心的 连线平行.
2. 实验现象
(1)不加磁场时,电子束的径迹是一条直线(图甲).加磁场后电子束的径迹是一个 圆(图乙).
(2)当电子束出射速度不变,磁感应强度变大时,这个圆的半径变小.
(3)当磁感应强度不变,电子束出射速度变大时,这个圆的半径变大.
3. 实验结论
带电粒子以垂直磁场的方向射入,在磁场中做匀速圆周运动,其运动规律与理论推导 相吻合.
研习 经典
A. 甲图中的电子束不受洛伦兹力
B. 乙图中的电子束不受洛伦兹力
C. 甲图中的电子束处在垂直纸面的磁场中
D. 乙图中的电子束处在平行纸面的磁场中
A
解析:甲图中的电子束的轨迹没有偏转,说明不受洛伦兹力,故A正确;乙图中的电 子束的轨迹发生偏转,说明受洛伦兹力,故B错误;甲图中的电子束的轨迹没有偏 转,说明不受洛伦兹力,电子束处在平行纸面的磁场中或处于磁感应强度为零的位 置,故C错误;乙图中的电子束的轨迹是圆周,说明受洛伦兹力,电子束处在垂直纸 面的磁场中,故D错误.
名师点评
解决此类问题时一定要清楚洛伦兹力演示仪的构造,洛伦兹力演示仪的两个励磁 线圈会产生垂直纸面的磁场,只要明确电子束的运动轨迹就可以确定电子束是否偏 转,是否受力.
对应 训练
B
A. 励磁线圈通以逆时针方向的电流,则能形成结构示意图中的电子运动径迹
B. 励磁线圈通以顺时针方向的电流,则能形成结构示意图中的电子运动径迹
C. 保持励磁电压不变,增加加速电压,电子束形成圆周的半径减小
D. 保持加速电压不变,增加励磁电压,电子束形成圆周的半径增大
第*页
研习任务三 带电粒子在匀强磁场中的圆周运动
合作 讨论
我们知道,在几何中,只要确定了一个圆的圆心和半径,这个圆就唯一确定了.带电 粒子在匀强磁场中做圆周运动,我们应该如何确定粒子运动的轨迹呢?
提示:要想确定粒子的运动轨迹,需要确定粒子做圆周运动的圆心和半径.圆心在入 射速度的垂线、出射速度的垂线和轨迹弦的垂直平分线上,以上三条线中任意两条线 的交点就是轨迹的圆心.粒子做圆周运动的半径可以根据几何关系或半径公式求解.
要点 归纳
在研究带电粒子在匀强磁场中做匀速圆周运动问题时,可以按照“找圆心,求半径, 求角度,解未知”的思路进行.
1. 找圆心——两线定一“心”
(1)圆心一定在垂直于速度的直线上.
如图甲所示,已知入射点P(或出射点M)的速度方向,可通过入射点和出射点作速 度的垂线,两条直线的交点就是圆心.
(2)圆心一定在弦的中垂线上.
如图乙所示,作P、M连线的中垂线,
与任一速度的垂线的交点为圆心.
(2)根据几何知识求解,如图所示.
3. 求角度
如图所示,
(1)带电粒子射出磁场的速度方向与射入磁场的速度方向之间的夹角φ叫作偏向角, 偏向角等于圆弧AB对应的圆心角α,即α=φ.
(2)圆弧AB所对应圆心角α等于弦AB与切线的夹角(弦切角)θ的2倍,即α=2θ.
(3)相对的弦切角相等;相邻的弦切角互补,即θ+θ'=180°.
(4)进出同一直边界时速度方向与该边界的夹角相等,如图所示.
研习 经典
B
名师点评
在解决此类问题时要熟悉“找圆心,求半径,解未知”三步曲,这三步要根据具 体情况来灵活使用,不一定每步都用到,也不一定有严格的先后顺序.
对应 训练
C. 2∶1
B
知识 构建
第*页
课后提素养 深刻剖析 提升能力
基础 题组
1. 判断正误.
√
×
×
×
×
×
A. 1∶1∶2 B. 1∶3∶4
C. 1∶1∶1
D
A. 若速率相等,则半径必相等
B. 若质量相等,则周期必相等
C. 若动量大小相等,则半径必相等
D. 若动能相等,则周期必相等
BC
中档 题组
A. 运动轨迹的半径是Ⅰ中的k倍
B. 加速度的大小是Ⅰ中的k倍
C. 做圆周运动的周期是Ⅰ中的k倍
D. 做圆周运动的角速度与Ⅰ中的相等
AC
A
3. 如图所示,一个质量为m、带负电荷、电荷量为q、不计重力的
带电粒子从x轴上的P点以速度v沿与x轴成60°的方向射入第一象限
内的匀强磁场中,并恰好垂直于y轴射出第一象限.已知OP=a,求:
(1)匀强磁场的磁感应强度B的大小;
(2)带电粒子穿过第一象限所用的时间.
第*页
课时作业(三)
[基础训练]
A. 它所受的洛伦兹力是恒定不变的
B. 它的速度是恒定不变的
C. 它的速度与磁感应强度B成正比
D. 它的运动周期与速度的大小无关
D
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
A. 1∶2,1∶2 B. 2∶1,2∶1
C. 2∶1,1∶2 D. 1∶2,2∶1
C
1
2
3
4
5
6
7
8
9
10
11
12
D
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
A. 1∶2 B. 2∶1
D. 1∶1
B
1
2
3
4
5
6
7
8
9
10
11
12
解析:画出正、负电子在磁场中运动的轨迹如图所示:
1
2
3
4
5
6
7
8
9
10
11
12
B
1
2
3
4
5
6
7
8
9
10
11
12
解析:根据题意作出正电荷运动的轨迹如图所示:
1
2
3
4
5
6
7
8
9
10
11
12
A. 粒子带正电,从B点射入
B. 粒子带负电,从B点射入
C. 粒子带正电,从A点射入
D. 粒子带负电,从A点射入
B
1
2
3
4
5
6
7
8
9
10
11
12
A. 粒子带正电
C. 粒子做圆周运动的半径为L
D
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
8. 一个带电荷量为+q,质量为m的粒子在磁感应强度为B的匀强磁场中以初速度v0垂 直于磁场自A点开始运动,如图所示,经时间t,粒子到达C点,求:
(1)画出粒子轨迹示意图;
答案:(1)见解析图
解析:(1)轨迹示意图如图所示
1
2
3
4
5
6
7
8
9
10
11
12
(2)粒子在磁场中运动的周期和加速度大小a;
1
2
3
4
5
6
7
8
9
10
11
12
(3)连接AC与v0所在直线间的夹角θ.
1
2
3
4
5
6
7
8
9
10
11
12
[能力提升]
A. 两个电子在磁场中运动的轨迹半径一定相同
B. 两个电子在磁场中运动的时间有可能相同
C. 进入圆形区域的电子一定先飞离磁场
D. 进入圆形区域的电子一定不会后飞离磁场
ABD
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
A. 电子将向右偏转
B. 电子打在MN上的点与O'点的距离为d
D
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
A. a、b两带电粒子的运动轨迹半径之比为1∶2
B. a、b两带电粒子的速度大小之比为2∶3
C. a、b两带电粒子的质量之比为2∶3
D. a、b两带电粒子的比荷之比为2∶3
AC
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
12. 在如图所示的平面直角坐标系Oxy中,有一个圆形区域的匀强磁场(图中未画 出),磁场方向垂直于Oxy平面,坐标原点为该圆形磁场区域的圆心.现有一质量为 m,带电荷量为+q的带电粒子(重力不计)从O点开始以初速度v沿x轴正方向进入磁 场,粒子经过y轴上P点时速度方向与y轴正方向夹角为θ=30°,已知OP=L,求:
(1)磁感应强度的大小;
1
2
3
4
5
6
7
8
9
10
11
12
解析:(1)依题意,粒子运动轨迹如图所示
1
2
3
4
5
6
7
8
9
10
11
12
(2)该圆形磁场区域的面积.
1
2
3
4
5
6
7
8
9
10
11
12
