第二十六章 反比例函数 单元练习(含答案) 人教版数学九年级下册
文档属性
| 名称 | 第二十六章 反比例函数 单元练习(含答案) 人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 173.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 00:00:00 | ||
图片预览



文档简介
反比例函数
一、选择题
1.下列关系式中, 是 反比例函数的是
A. B. C. D.
2.若反比例函数的图象经过 ,,则
A. B. C. D.
3.已知反比例函数 ,下列结论正确的是
A. 的值随着 的增大而减小
B.图象位于一、三象限
C.图象是中心对称图形也是轴对称图形
D.图象可能与坐标轴相交
4.在同一直角坐标系中,函数 与 的图象大致是
A. B.
C. D.
5.如图,反比例函数 的图象与直线 的交点为 ,,过 作 轴的平行线与过点 作 轴的平行线相交于点 ,则 的面积为
A. B. C. D.
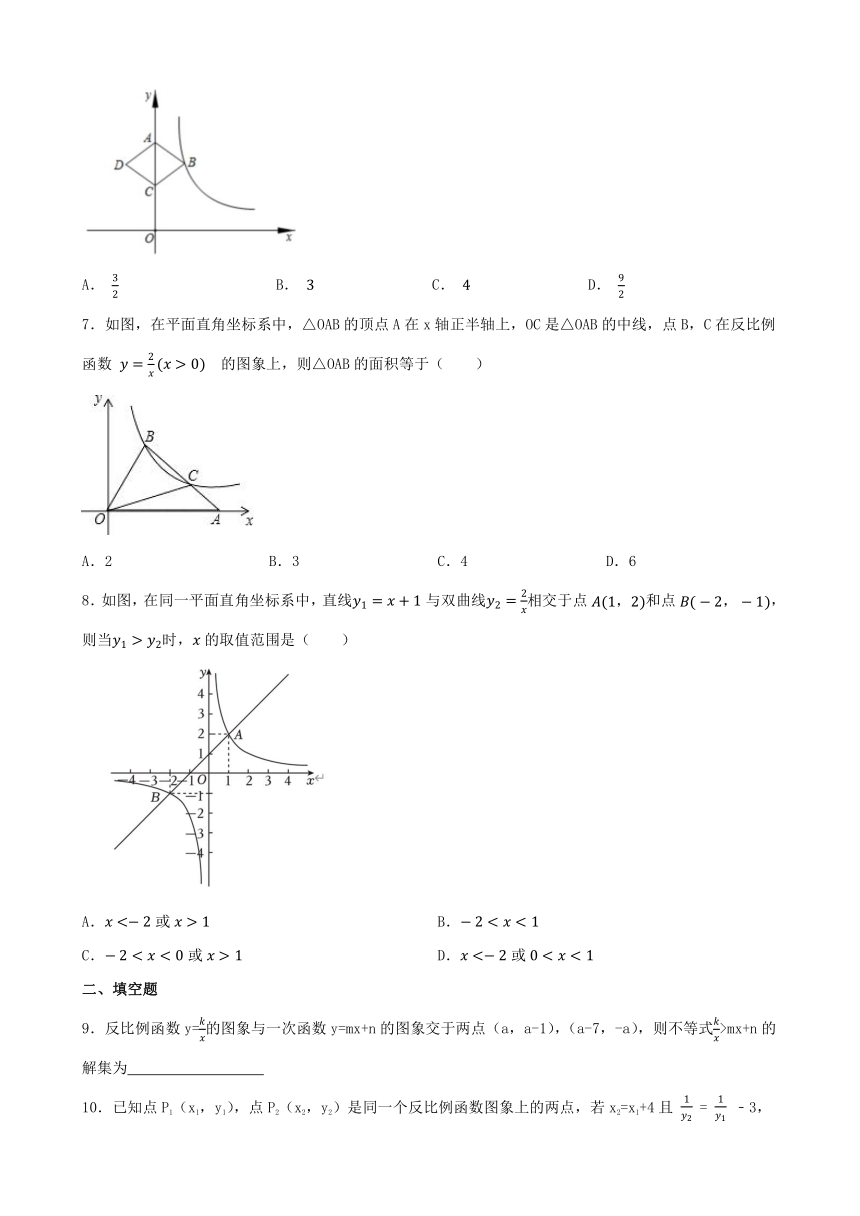
6.如图所示,菱形 的顶点 , 在 轴正半轴上,反比例函数 经过顶点 ,若点 为 中点,菱形 的面积 ,则 的值为
A. B. C. D.
7.如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数 的图象上,则△OAB的面积等于( )
A.2 B.3 C.4 D.6
8.如图,在同一平面直角坐标系中,直线与双曲线相交于点和点,则当时,的取值范围是( )
A.或 B.
C.或 D.或
二、填空题
9.反比例函数y=的图象与一次函数y=mx+n的图象交于两点(a,a-1),(a-7,-a),则不等式>mx+n的解集为
10.已知点P1(x1,y1),点P2(x2,y2)是同一个反比例函数图象上的两点,若x2=x1+4且 = ﹣3,则这个反比例函数的表达式为 .
11.如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=kx(x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为
12.如图, 和 都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数 在第一象限的图象经过点B,则 和 的面积之差为 .
13.如图,△OB1A1,△A1B2A2,△A2B3A3,…△An﹣1BnAn均为等边三角形,其中点A1,A2,A3,…An都在x轴上,点B1,B2,B3,…,Bn都在反比例函数的图象上,则An的坐标为 .
三、解答题
14.反比例函数y= (k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.
15.小明在某一次实验中,测得两个变量之间的关系如下表所示:
x 1 2 3 4 12
y 12.03 5.98 3.03 1.99 1.00
请你根据表格回答下列问题:
①这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由;
②请你写出这个函数的解析式;
③表格中空缺的数值可能是多少?请你给出合理的数值.
16.如图,已知反比例函数 的图象与一次函数 的图象在第一象限交于 两点
(1)求反比例函数和一次函数的表达式;
(2)已知点 ,过点 作平行于 轴的直线,在第一象限内交一次函数 的图象于点 ,交反比例函数 上的图象于点 .若 ,结合函数图象直接写出 的取值范围.
17.如图,在平面系中,一次函数 的图像经过定点A,反比例函数 的图像经过点A,且与一次函数 的图像相交于点B( ,m).
(1)求m、a的值;
(2)设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式 的值.
18.某企业员工感冒后,到药店买了一种新型感冒药,按使用说明书服用后,血液中的约物浓度(微克/亳升)与服药后时间(小时)之间的函数关系如下图所示,其中,当时,满足的关系式;当时,与成反比例.
(1)求的值,并求当时,与的函数关系式;
(2)若血液中药物浓度不低于2.5微克/敦升的持续时间超过5.5小时,则称药物治疗有效,请通过计算说明用这种新药治疗是否有效吗?
答案
1. B
2. D
3. C
4. D
5. A
6. D
7.B
8.C
9.或
10.y=﹣
11.(4,)
12.3
13.
14.(1)解:把A(1,2k﹣1)代入y= 得,
2k﹣1=k,
∴k=1,
∴反比例函数的解析式为:y=
(2)解:由(1)得k=1,
∴A(1,1),
设B(a,0),
∴S△AOB= |a|×1=3,
∴a=±6,
∴B(﹣6,0)或(6,0),
把A(1,1),B(﹣6,0)代入y=mx+b得: ,
∴ ,
∴一次函数的解析式为:y= x+ ,
把A(1,1),B(6,0)代入y=mx+b得: ,
∴ ,
∴一次函数的解析式为:y=﹣ .
所以符合条件的一次函数解析式为:y=﹣ 或y= x+
15.解:①由表中自变量x和因变量y的数值可知:
自变量x和因变量y的乘积都大约等于12,且随着自变量x值的逐渐增加,因变量y的值逐渐减少,
故两个变量x和y之间可能是反比例函数关系.
②∵两自变量的乘积等于12,
且两自变量为反比例函数关系,
∴ ;
③将x=3代入得:y=4;
将y=1.99代入得:x≈6.
故表格中x的空值填6,y的空值填4
16.(1)解:∵反比例函数 的图象与一次函数 的图象在第一象限交于 两点,
∴ ,
∴ ,
∴反比例函数和一次函数的表达式分别为 ;
(2)解:由图象可得:当 时, .
17.(1)解:由 的图像经过定点A,则A点的坐标为(1,6)
将A(1,6)代入 得,k=6
∴反比例函数的解析式为
又∵点B( ,m)在反比例函数图象上
∴ ,即B点坐标为(-3,-2)
∴-2=-3a-a+6,即a=2
故答案为a=2,m=-2;
(2)解:如图,连接AP,BP,过点P作PE⊥x轴交AB于点E,
由(1)知y=,一次函数y=2x+4,
设P(n,),则E(n,2n+4),∴PE=2n+4-,
∴S△ABP=·PE·(xA-xB)=×(2n+4-)×4=12,
∴n2-n=3.
18.(1)解:由图象可知,将(3,6)代入函数,
得6=3t,解得t=2,
当时,设与的函数关系式为
将(3,6)代入,得,
,
(2)解:将代入函数得,解得,
将代入函数得,
解得,
这种新药治疗有效
一、选择题
1.下列关系式中, 是 反比例函数的是
A. B. C. D.
2.若反比例函数的图象经过 ,,则
A. B. C. D.
3.已知反比例函数 ,下列结论正确的是
A. 的值随着 的增大而减小
B.图象位于一、三象限
C.图象是中心对称图形也是轴对称图形
D.图象可能与坐标轴相交
4.在同一直角坐标系中,函数 与 的图象大致是
A. B.
C. D.
5.如图,反比例函数 的图象与直线 的交点为 ,,过 作 轴的平行线与过点 作 轴的平行线相交于点 ,则 的面积为
A. B. C. D.
6.如图所示,菱形 的顶点 , 在 轴正半轴上,反比例函数 经过顶点 ,若点 为 中点,菱形 的面积 ,则 的值为
A. B. C. D.
7.如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数 的图象上,则△OAB的面积等于( )
A.2 B.3 C.4 D.6
8.如图,在同一平面直角坐标系中,直线与双曲线相交于点和点,则当时,的取值范围是( )
A.或 B.
C.或 D.或
二、填空题
9.反比例函数y=的图象与一次函数y=mx+n的图象交于两点(a,a-1),(a-7,-a),则不等式>mx+n的解集为
10.已知点P1(x1,y1),点P2(x2,y2)是同一个反比例函数图象上的两点,若x2=x1+4且 = ﹣3,则这个反比例函数的表达式为 .
11.如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=kx(x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为
12.如图, 和 都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数 在第一象限的图象经过点B,则 和 的面积之差为 .
13.如图,△OB1A1,△A1B2A2,△A2B3A3,…△An﹣1BnAn均为等边三角形,其中点A1,A2,A3,…An都在x轴上,点B1,B2,B3,…,Bn都在反比例函数的图象上,则An的坐标为 .
三、解答题
14.反比例函数y= (k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.
15.小明在某一次实验中,测得两个变量之间的关系如下表所示:
x 1 2 3 4 12
y 12.03 5.98 3.03 1.99 1.00
请你根据表格回答下列问题:
①这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由;
②请你写出这个函数的解析式;
③表格中空缺的数值可能是多少?请你给出合理的数值.
16.如图,已知反比例函数 的图象与一次函数 的图象在第一象限交于 两点
(1)求反比例函数和一次函数的表达式;
(2)已知点 ,过点 作平行于 轴的直线,在第一象限内交一次函数 的图象于点 ,交反比例函数 上的图象于点 .若 ,结合函数图象直接写出 的取值范围.
17.如图,在平面系中,一次函数 的图像经过定点A,反比例函数 的图像经过点A,且与一次函数 的图像相交于点B( ,m).
(1)求m、a的值;
(2)设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式 的值.
18.某企业员工感冒后,到药店买了一种新型感冒药,按使用说明书服用后,血液中的约物浓度(微克/亳升)与服药后时间(小时)之间的函数关系如下图所示,其中,当时,满足的关系式;当时,与成反比例.
(1)求的值,并求当时,与的函数关系式;
(2)若血液中药物浓度不低于2.5微克/敦升的持续时间超过5.5小时,则称药物治疗有效,请通过计算说明用这种新药治疗是否有效吗?
答案
1. B
2. D
3. C
4. D
5. A
6. D
7.B
8.C
9.或
10.y=﹣
11.(4,)
12.3
13.
14.(1)解:把A(1,2k﹣1)代入y= 得,
2k﹣1=k,
∴k=1,
∴反比例函数的解析式为:y=
(2)解:由(1)得k=1,
∴A(1,1),
设B(a,0),
∴S△AOB= |a|×1=3,
∴a=±6,
∴B(﹣6,0)或(6,0),
把A(1,1),B(﹣6,0)代入y=mx+b得: ,
∴ ,
∴一次函数的解析式为:y= x+ ,
把A(1,1),B(6,0)代入y=mx+b得: ,
∴ ,
∴一次函数的解析式为:y=﹣ .
所以符合条件的一次函数解析式为:y=﹣ 或y= x+
15.解:①由表中自变量x和因变量y的数值可知:
自变量x和因变量y的乘积都大约等于12,且随着自变量x值的逐渐增加,因变量y的值逐渐减少,
故两个变量x和y之间可能是反比例函数关系.
②∵两自变量的乘积等于12,
且两自变量为反比例函数关系,
∴ ;
③将x=3代入得:y=4;
将y=1.99代入得:x≈6.
故表格中x的空值填6,y的空值填4
16.(1)解:∵反比例函数 的图象与一次函数 的图象在第一象限交于 两点,
∴ ,
∴ ,
∴反比例函数和一次函数的表达式分别为 ;
(2)解:由图象可得:当 时, .
17.(1)解:由 的图像经过定点A,则A点的坐标为(1,6)
将A(1,6)代入 得,k=6
∴反比例函数的解析式为
又∵点B( ,m)在反比例函数图象上
∴ ,即B点坐标为(-3,-2)
∴-2=-3a-a+6,即a=2
故答案为a=2,m=-2;
(2)解:如图,连接AP,BP,过点P作PE⊥x轴交AB于点E,
由(1)知y=,一次函数y=2x+4,
设P(n,),则E(n,2n+4),∴PE=2n+4-,
∴S△ABP=·PE·(xA-xB)=×(2n+4-)×4=12,
∴n2-n=3.
18.(1)解:由图象可知,将(3,6)代入函数,
得6=3t,解得t=2,
当时,设与的函数关系式为
将(3,6)代入,得,
,
(2)解:将代入函数得,解得,
将代入函数得,
解得,
这种新药治疗有效
