【期末专项培优】轴对称(含解析)2024-2025学年华东师大版(2024)数学七年级下册
文档属性
| 名称 | 【期末专项培优】轴对称(含解析)2024-2025学年华东师大版(2024)数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1007.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 00:00:00 | ||
图片预览



文档简介
期末专项培优 轴对称
一.选择题(共5小题)
1.(2024秋 巢湖市期末)下列图形不是轴对称图形的是( )
A. B.
C. D.
2.(2024秋 伊川县期末)如图,在△ABC中,边AB的垂直平分线分别交AC于点D,交AB于点E,若AE=3,△BCD的周长为8,则△ABC的周长为( )
A.8 B.11 C.14 D.18
3.(2024秋 海曙区期末)如图,已知,AB=8,BC=4,分别以A,B两点为圆心,以大于的长为半径画圆弧,两弧相交于点D,E,直线DE分别交AB,AC于点F,G,则CG长的取值范围为( )
A.1<CG<3 B.2<CG<6
C.2.5<CG<4.5 D.3<CG<5
4.(2024秋 盐城期末)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A.山 B.河 C.无 D.恙
5.(2024秋 长沙期末)2024年10月30日4时27分,搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉卫星发射中心发射升空,约10分钟后,神舟十九号载人飞船与火箭分离成功,进入预定轨道,发射取得圆满成功!下列是同学们设计的神舟20号飞船简笔画,其中是轴对称图形的是( )
A.
B.
C.
D.
二.填空题(共5小题)
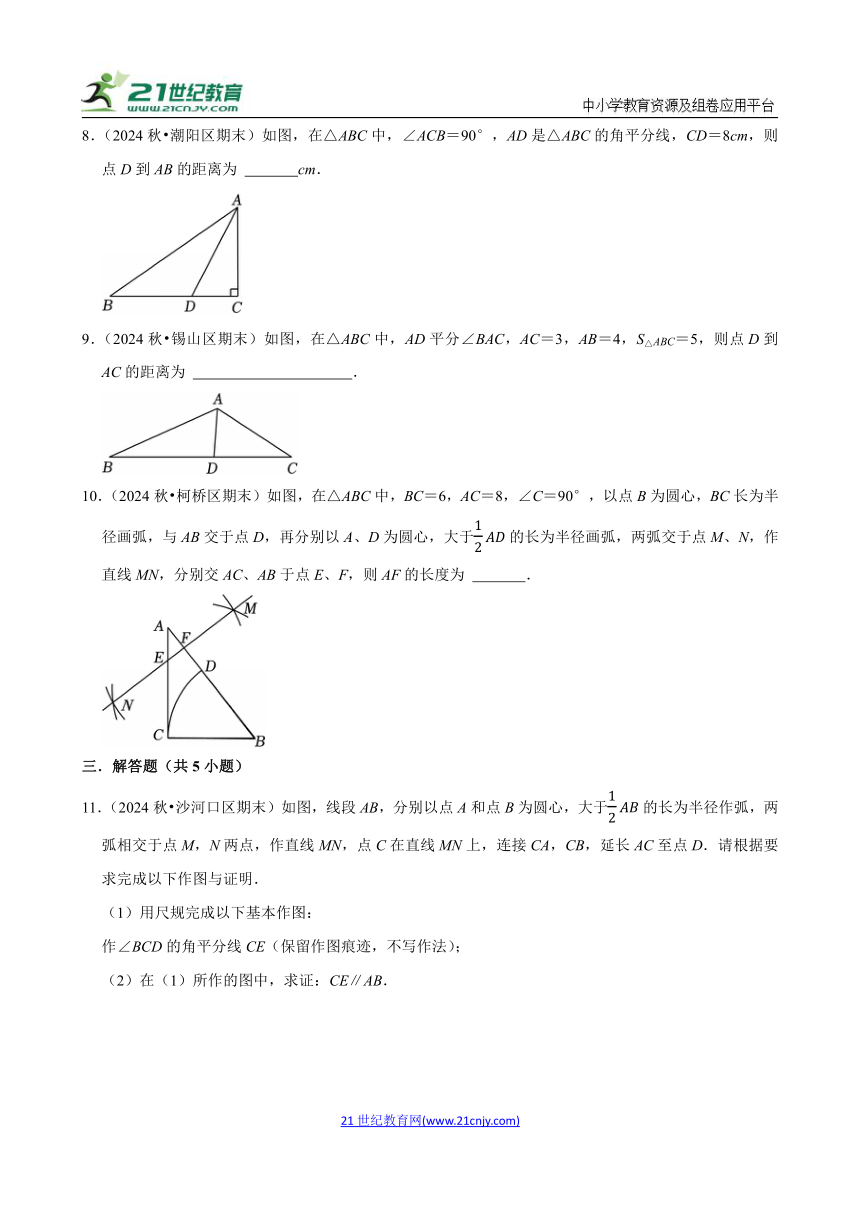
6.(2024秋 鼓楼区校级期末)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,DC=3,则点D到AB的距离是 .
7.(2024秋 高邮市期末)如图,在△ABC中,BC的垂直平分线分别交AC、BC于点D、E.若△ABC的周长为20,BE=6,则△ABD的周长为 .
8.(2024秋 潮阳区期末)如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,CD=8cm,则点D到AB的距离为 cm.
9.(2024秋 锡山区期末)如图,在△ABC中,AD平分∠BAC,AC=3,AB=4,S△ABC=5,则点D到AC的距离为 .
10.(2024秋 柯桥区期末)如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AF的长度为 .
三.解答题(共5小题)
11.(2024秋 沙河口区期末)如图,线段AB,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点M,N两点,作直线MN,点C在直线MN上,连接CA,CB,延长AC至点D.请根据要求完成以下作图与证明.
(1)用尺规完成以下基本作图:
作∠BCD的角平分线CE(保留作图痕迹,不写作法);
(2)在(1)所作的图中,求证:CE∥AB.
12.(2024秋 南岸区期末)已知:∠ABC=α,∠CBD=90°,用尺规完成下列作图,并回答问题.
(1)求作:以点B为顶点;射线BC为一边,在∠ABC外作∠CBE,使∠CBE=∠ABC;(不写作法,保留作图痕迹)
(2)延长AB至F,用等式表示图中所有相等的角,以及和为90°的角.
13.(2024秋 大足区期末)如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(﹣1,5),B(﹣2,0),C(﹣4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
14.(2024秋 平潭县期末)如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.
15.(2024秋 泰兴市期末)如图,∠ACD是△ABC的一个外角.
(1)利用无刻度的直尺和圆规作图:在∠ACD的内部画射线CE,使CE∥AB(不写作法,保留作图痕迹);
(2)在(1)的条件下,若射线CE是∠ACD的平分线,∠B=54°,求∠A的度数.
期末专项培优 轴对称
参考答案与试题解析
题号 1 2 3 4 5
答案 C C B A B
一.选择题(共5小题)
1.(2024秋 巢湖市期末)下列图形不是轴对称图形的是( )
A. B.
C. D.
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】C
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:A、B、D选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
C选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是不轴对称图形;
故选:C.
【点评】本题考查了轴对称图形的识别,理解轴对称定义是关键.
2.(2024秋 伊川县期末)如图,在△ABC中,边AB的垂直平分线分别交AC于点D,交AB于点E,若AE=3,△BCD的周长为8,则△ABC的周长为( )
A.8 B.11 C.14 D.18
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】C
【分析】根据线段的垂直平分线的性质得到DA=DB,AB=2AE=6,根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是线段AB的垂直平分线,
∴AB=2AE=6,DA=DB,
∵△BCD的周长为8,
∴BD+CD+BC=8,
∴AD+CD+BC=8,
∴AC+BC=8,
∵AB=6,
∴△ABC的周长=AB+BC+AC=6+8=14,
故选:C.
【点评】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
3.(2024秋 海曙区期末)如图,已知,AB=8,BC=4,分别以A,B两点为圆心,以大于的长为半径画圆弧,两弧相交于点D,E,直线DE分别交AB,AC于点F,G,则CG长的取值范围为( )
A.1<CG<3 B.2<CG<6
C.2.5<CG<4.5 D.3<CG<5
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题;推理能力.
【答案】B
【分析】由已知条件和三角形内角和定理证得∠B=∠C,得到AB=AC=8,设CG=x,则AG=8﹣x,连接BG,根据线段垂直平分线的性质得到BG=AG=8﹣x,在△BCG中,根据三角形的三边关系即可求得答案.
【解答】解:∵∠B∠A=90°,
∴2∠B+∠A=180°,
∵∠B+∠C+∠A=180°,
∴∠B=∠C,
∴AB=AC=8,
设CG=x,则AG=8﹣x,
连接BG,
由作图可知,AG是线段AB的垂直平分线,
∴BG=AG=8﹣x,
在△BCG中,,
解得2<x<6,即2<CG<6,
故选:B.
【点评】本题考查了作图﹣基本作图,三角形内角和定理,线段垂直平分线的性质,三角形三边关系定理,等腰三角形的判定,灵活掌握相关知识是解决此题的关键.
4.(2024秋 盐城期末)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A.山 B.河 C.无 D.恙
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:B、C、D选项中的汉字都不能找到这样的一条直线,使汉字沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称汉字;
A选项中的汉字能找到这样的一条直线,使汉字沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称汉字;
故选:A.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
5.(2024秋 长沙期末)2024年10月30日4时27分,搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉卫星发射中心发射升空,约10分钟后,神舟十九号载人飞船与火箭分离成功,进入预定轨道,发射取得圆满成功!下列是同学们设计的神舟20号飞船简笔画,其中是轴对称图形的是( )
A.
B.
C.
D.
【考点】轴对称图形.
【专题】几何直观.
【答案】B
【分析】根据轴对称图形的定义进行逐一判断即可.
【解答】解:选项A、C、D均不能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以不是轴对称图形,不符合题意;
选项B能找到这样一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以是轴对称图形,符合题意;
故选:B.
【点评】本题主要考查了轴对称图形的定义,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.
二.填空题(共5小题)
6.(2024秋 鼓楼区校级期末)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,DC=3,则点D到AB的距离是 3 .
【考点】角平分线的性质;点到直线的距离.
【专题】线段、角、相交线与平行线;运算能力.
【答案】3.
【分析】根据角平分线的性质即可得到答案.
【解答】解:过D作DE⊥AB交AB于点E,
∵∠ACB=90°,AD平分∠BAC,
∴DE=DC,
∵DC=3,
∴DE=DC=3,
∴D到AB的距离是3.
故答案为:3.
【点评】本题主要考查角平分线的性质,掌握角平分线的性质是解题的关键.
7.(2024秋 高邮市期末)如图,在△ABC中,BC的垂直平分线分别交AC、BC于点D、E.若△ABC的周长为20,BE=6,则△ABD的周长为 8 .
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】8.
【分析】根据线段的垂直平分线的性质得到DB=DC,BC=2BE=12,再根据三角形周长公式计算即可.
【解答】解:∵DE是BC的垂直平分线,BE=6,
∴DB=DC,BC=2BE=12,
∵△ABC的周长为20,
∴AB+AC+BC=20,
∴AB+AC=20﹣12=8,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=8,
故答案为:8.
【点评】本题考查的是线段的垂直平分线的性质,线段的垂直平分线上的点到线段的两个端点的距离相等.
8.(2024秋 潮阳区期末)如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,CD=8cm,则点D到AB的距离为 8 cm.
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】8.
【分析】过点D作DH⊥AB于H,由角平分线上的点到角两边的距离相等得到DH=CD=8cm,即可得到D到AB的距离为8cm.
【解答】解:如图所示,过点D作DH⊥AB于H,
,
∵AD是△ABC的角平分线,∠ACB=90°,DH⊥AB,CD=8cm,
∴DH=CD=8cm,
∴D到AB的距离为8cm,
故答案为:8.
【点评】本题主要考查了角平分线的性质,解答本题的关键要明确:角平分线上的点到角的两边的距离相等.
9.(2024秋 锡山区期末)如图,在△ABC中,AD平分∠BAC,AC=3,AB=4,S△ABC=5,则点D到AC的距离为 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】.
【分析】过D点作DE⊥AB,DF⊥AC,垂足分别为E,F,由角平分线的性质可得DE=DF,再利用三角形的面积公式计算可求解.
【解答】解:过D点作DE⊥AB,DF⊥AC,垂足分别为E,F,
∵AD平分∠BAC,
∴DE=DF,
∵AB=4,AC=3,
∴S△ABCAB DEAC DF=2DEDFDF=5,
∴DF,
∴点D到AC的距离为.
故答案为:.
【点评】本题主要考查角平分线的性质,根据角平分线的性质得DE=DF是解题的关键.
10.(2024秋 柯桥区期末)如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AF的长度为 2 .
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题;运算能力;推理能力.
【答案】2.
【分析】由题意得,BC=BD=6,直线MN为线段AD的垂直平分线,由勾股定理得AB=10,进而可得AF=2.
【解答】解:由题意得,BC=BD=6,直线MN为线段AD的垂直平分线,
∵BC=6,AC=8,∠C=90°,
∴AB10,
∴AD=AB﹣BD=4,
∴AF2,
故答案为:2.
【点评】本题考查作图﹣基本作图、勾股定理、线段垂直平分线、相似三角形的判定与性质,熟练掌握相关知识点是解答本题的关键.
三.解答题(共5小题)
11.(2024秋 沙河口区期末)如图,线段AB,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点M,N两点,作直线MN,点C在直线MN上,连接CA,CB,延长AC至点D.请根据要求完成以下作图与证明.
(1)用尺规完成以下基本作图:
作∠BCD的角平分线CE(保留作图痕迹,不写作法);
(2)在(1)所作的图中,求证:CE∥AB.
【考点】作图—复杂作图;平行线的判定;线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;尺规作图;几何直观.
【答案】(1)见解答.
(2)见解答.
【分析】(1)根据角平分线的作图方法作图即可.
(2)由作图过程可知,直线MN为线段AB的垂直平分线,可得CA=CB,则∠A=∠B,进而可得∠BCD=2∠B,即.由角平分线的定义可得,则∠B=∠BCE,即CE∥AB.
【解答】(1)解:如图,射线CE即为所求.
(2)证明:由作图过程可知,直线MN为线段AB的垂直平分线,
∴CA=CB,
∴∠A=∠B.
∵∠BCD=∠A+∠B,
∴∠BCD=2∠B,
即.
∵CE平分∠BCD,
∴,
∴∠B=∠BCE.
∴CE∥AB.
【点评】本题考查作图—复杂作图、平行线的判定、线段垂直平分线的性质,熟练掌握平行线的判定、线段垂直平分线的性质是解答本题的关键.
12.(2024秋 南岸区期末)已知:∠ABC=α,∠CBD=90°,用尺规完成下列作图,并回答问题.
(1)求作:以点B为顶点;射线BC为一边,在∠ABC外作∠CBE,使∠CBE=∠ABC;(不写作法,保留作图痕迹)
(2)延长AB至F,用等式表示图中所有相等的角,以及和为90°的角.
【考点】作图—基本作图;余角和补角.
【专题】几何直观.
【答案】(1)见解析;
(2)见解析.
【分析】(1)根据作一个角等于已知角的方法,作图即可;
(2)根据图形,结合∠ABC=∠CBE,同角或等角的余角相等,进行判断解答即可.
【解答】解:(1)如图所示,∠CBE即为所求作;
(2)相等的角有:∠ABC=∠CBE,∠EBD=∠FBD;
和为90°的角有:∠ABC+∠DBE=90°,∠ABC+∠FBD=90°,∠CBE+∠EBD=90°,∠CBE+∠FBD=90°.
【点评】本题主要考查作一个角等于已知角,余角的性质,解题的关键是熟练掌握作一个角等于已知角的方法.
13.(2024秋 大足区期末)如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(﹣1,5),B(﹣2,0),C(﹣4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
【考点】作图﹣轴对称变换.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)根据网格结构找出点A、B、C关于y轴对称的点A1、B1、C1的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标即可;
(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
【解答】解:(1)△A1B1C1如图所示;
(2)A1(1,5)B1(2,0)C1(4,3);
(3)△A1B1C1的面积=3×51×52×32×3,
=15﹣2.5﹣3﹣3,
=15﹣8.5,
=6.5.
【点评】本题考查了利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
14.(2024秋 平潭县期末)如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)作线段AB的垂直平分线即可;
(2)根据线段垂直平分线的性质可得BP=AP,根据等边对等角可得∠B=∠PAB,然后再根据角平分线定义可得∠CAP=∠PAB,进而可得∠B=∠PAB=∠CAP,然后可得答案.
【解答】解:(1)如图,点P为所作;
(2)∵点P在AB的垂直平分线MN上
∴PA=PB,
∴∠B=∠PAB,
∵AP平分∠CAB,
∴∠PAB∠CAB,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
即2∠B+∠B=90°,
∴∠B=30°.
【点评】此题主要考查了基本作图,以及线段垂直平分线的性质,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
15.(2024秋 泰兴市期末)如图,∠ACD是△ABC的一个外角.
(1)利用无刻度的直尺和圆规作图:在∠ACD的内部画射线CE,使CE∥AB(不写作法,保留作图痕迹);
(2)在(1)的条件下,若射线CE是∠ACD的平分线,∠B=54°,求∠A的度数.
【考点】作图—复杂作图;平行线的判定与性质.
【专题】尺规作图;几何直观.
【答案】(1)作图见解析;
(2)54°.
【分析】(1)作∠DCE=∠B即可得到CE∥AB;
(2)由CE∥AB可得∠B=∠DCE=54°,∠A=∠ACE,再结合角平分线的定义可得答案.
【解答】解:(1)如图,CE即为所求;
(2)∵CE∥AB,
∴∠B=∠DCE=54°,∠A=∠ACE,
∵CE是∠ACD的平分线,
∴∠ACE=∠DCE,
∴∠A=∠B=54°.
【点评】本题考查作图﹣复杂作图,平行线的判定与性质,解答本题的关键是熟练掌握画一个角等于已知角的方法.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 巢湖市期末)下列图形不是轴对称图形的是( )
A. B.
C. D.
2.(2024秋 伊川县期末)如图,在△ABC中,边AB的垂直平分线分别交AC于点D,交AB于点E,若AE=3,△BCD的周长为8,则△ABC的周长为( )
A.8 B.11 C.14 D.18
3.(2024秋 海曙区期末)如图,已知,AB=8,BC=4,分别以A,B两点为圆心,以大于的长为半径画圆弧,两弧相交于点D,E,直线DE分别交AB,AC于点F,G,则CG长的取值范围为( )
A.1<CG<3 B.2<CG<6
C.2.5<CG<4.5 D.3<CG<5
4.(2024秋 盐城期末)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A.山 B.河 C.无 D.恙
5.(2024秋 长沙期末)2024年10月30日4时27分,搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉卫星发射中心发射升空,约10分钟后,神舟十九号载人飞船与火箭分离成功,进入预定轨道,发射取得圆满成功!下列是同学们设计的神舟20号飞船简笔画,其中是轴对称图形的是( )
A.
B.
C.
D.
二.填空题(共5小题)
6.(2024秋 鼓楼区校级期末)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,DC=3,则点D到AB的距离是 .
7.(2024秋 高邮市期末)如图,在△ABC中,BC的垂直平分线分别交AC、BC于点D、E.若△ABC的周长为20,BE=6,则△ABD的周长为 .
8.(2024秋 潮阳区期末)如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,CD=8cm,则点D到AB的距离为 cm.
9.(2024秋 锡山区期末)如图,在△ABC中,AD平分∠BAC,AC=3,AB=4,S△ABC=5,则点D到AC的距离为 .
10.(2024秋 柯桥区期末)如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AF的长度为 .
三.解答题(共5小题)
11.(2024秋 沙河口区期末)如图,线段AB,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点M,N两点,作直线MN,点C在直线MN上,连接CA,CB,延长AC至点D.请根据要求完成以下作图与证明.
(1)用尺规完成以下基本作图:
作∠BCD的角平分线CE(保留作图痕迹,不写作法);
(2)在(1)所作的图中,求证:CE∥AB.
12.(2024秋 南岸区期末)已知:∠ABC=α,∠CBD=90°,用尺规完成下列作图,并回答问题.
(1)求作:以点B为顶点;射线BC为一边,在∠ABC外作∠CBE,使∠CBE=∠ABC;(不写作法,保留作图痕迹)
(2)延长AB至F,用等式表示图中所有相等的角,以及和为90°的角.
13.(2024秋 大足区期末)如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(﹣1,5),B(﹣2,0),C(﹣4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
14.(2024秋 平潭县期末)如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.
15.(2024秋 泰兴市期末)如图,∠ACD是△ABC的一个外角.
(1)利用无刻度的直尺和圆规作图:在∠ACD的内部画射线CE,使CE∥AB(不写作法,保留作图痕迹);
(2)在(1)的条件下,若射线CE是∠ACD的平分线,∠B=54°,求∠A的度数.
期末专项培优 轴对称
参考答案与试题解析
题号 1 2 3 4 5
答案 C C B A B
一.选择题(共5小题)
1.(2024秋 巢湖市期末)下列图形不是轴对称图形的是( )
A. B.
C. D.
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】C
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:A、B、D选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
C选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是不轴对称图形;
故选:C.
【点评】本题考查了轴对称图形的识别,理解轴对称定义是关键.
2.(2024秋 伊川县期末)如图,在△ABC中,边AB的垂直平分线分别交AC于点D,交AB于点E,若AE=3,△BCD的周长为8,则△ABC的周长为( )
A.8 B.11 C.14 D.18
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】C
【分析】根据线段的垂直平分线的性质得到DA=DB,AB=2AE=6,根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是线段AB的垂直平分线,
∴AB=2AE=6,DA=DB,
∵△BCD的周长为8,
∴BD+CD+BC=8,
∴AD+CD+BC=8,
∴AC+BC=8,
∵AB=6,
∴△ABC的周长=AB+BC+AC=6+8=14,
故选:C.
【点评】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
3.(2024秋 海曙区期末)如图,已知,AB=8,BC=4,分别以A,B两点为圆心,以大于的长为半径画圆弧,两弧相交于点D,E,直线DE分别交AB,AC于点F,G,则CG长的取值范围为( )
A.1<CG<3 B.2<CG<6
C.2.5<CG<4.5 D.3<CG<5
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题;推理能力.
【答案】B
【分析】由已知条件和三角形内角和定理证得∠B=∠C,得到AB=AC=8,设CG=x,则AG=8﹣x,连接BG,根据线段垂直平分线的性质得到BG=AG=8﹣x,在△BCG中,根据三角形的三边关系即可求得答案.
【解答】解:∵∠B∠A=90°,
∴2∠B+∠A=180°,
∵∠B+∠C+∠A=180°,
∴∠B=∠C,
∴AB=AC=8,
设CG=x,则AG=8﹣x,
连接BG,
由作图可知,AG是线段AB的垂直平分线,
∴BG=AG=8﹣x,
在△BCG中,,
解得2<x<6,即2<CG<6,
故选:B.
【点评】本题考查了作图﹣基本作图,三角形内角和定理,线段垂直平分线的性质,三角形三边关系定理,等腰三角形的判定,灵活掌握相关知识是解决此题的关键.
4.(2024秋 盐城期末)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A.山 B.河 C.无 D.恙
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:B、C、D选项中的汉字都不能找到这样的一条直线,使汉字沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称汉字;
A选项中的汉字能找到这样的一条直线,使汉字沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称汉字;
故选:A.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
5.(2024秋 长沙期末)2024年10月30日4时27分,搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉卫星发射中心发射升空,约10分钟后,神舟十九号载人飞船与火箭分离成功,进入预定轨道,发射取得圆满成功!下列是同学们设计的神舟20号飞船简笔画,其中是轴对称图形的是( )
A.
B.
C.
D.
【考点】轴对称图形.
【专题】几何直观.
【答案】B
【分析】根据轴对称图形的定义进行逐一判断即可.
【解答】解:选项A、C、D均不能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以不是轴对称图形,不符合题意;
选项B能找到这样一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以是轴对称图形,符合题意;
故选:B.
【点评】本题主要考查了轴对称图形的定义,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.
二.填空题(共5小题)
6.(2024秋 鼓楼区校级期末)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,DC=3,则点D到AB的距离是 3 .
【考点】角平分线的性质;点到直线的距离.
【专题】线段、角、相交线与平行线;运算能力.
【答案】3.
【分析】根据角平分线的性质即可得到答案.
【解答】解:过D作DE⊥AB交AB于点E,
∵∠ACB=90°,AD平分∠BAC,
∴DE=DC,
∵DC=3,
∴DE=DC=3,
∴D到AB的距离是3.
故答案为:3.
【点评】本题主要考查角平分线的性质,掌握角平分线的性质是解题的关键.
7.(2024秋 高邮市期末)如图,在△ABC中,BC的垂直平分线分别交AC、BC于点D、E.若△ABC的周长为20,BE=6,则△ABD的周长为 8 .
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】8.
【分析】根据线段的垂直平分线的性质得到DB=DC,BC=2BE=12,再根据三角形周长公式计算即可.
【解答】解:∵DE是BC的垂直平分线,BE=6,
∴DB=DC,BC=2BE=12,
∵△ABC的周长为20,
∴AB+AC+BC=20,
∴AB+AC=20﹣12=8,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=8,
故答案为:8.
【点评】本题考查的是线段的垂直平分线的性质,线段的垂直平分线上的点到线段的两个端点的距离相等.
8.(2024秋 潮阳区期末)如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,CD=8cm,则点D到AB的距离为 8 cm.
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】8.
【分析】过点D作DH⊥AB于H,由角平分线上的点到角两边的距离相等得到DH=CD=8cm,即可得到D到AB的距离为8cm.
【解答】解:如图所示,过点D作DH⊥AB于H,
,
∵AD是△ABC的角平分线,∠ACB=90°,DH⊥AB,CD=8cm,
∴DH=CD=8cm,
∴D到AB的距离为8cm,
故答案为:8.
【点评】本题主要考查了角平分线的性质,解答本题的关键要明确:角平分线上的点到角的两边的距离相等.
9.(2024秋 锡山区期末)如图,在△ABC中,AD平分∠BAC,AC=3,AB=4,S△ABC=5,则点D到AC的距离为 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】.
【分析】过D点作DE⊥AB,DF⊥AC,垂足分别为E,F,由角平分线的性质可得DE=DF,再利用三角形的面积公式计算可求解.
【解答】解:过D点作DE⊥AB,DF⊥AC,垂足分别为E,F,
∵AD平分∠BAC,
∴DE=DF,
∵AB=4,AC=3,
∴S△ABCAB DEAC DF=2DEDFDF=5,
∴DF,
∴点D到AC的距离为.
故答案为:.
【点评】本题主要考查角平分线的性质,根据角平分线的性质得DE=DF是解题的关键.
10.(2024秋 柯桥区期末)如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AF的长度为 2 .
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题;运算能力;推理能力.
【答案】2.
【分析】由题意得,BC=BD=6,直线MN为线段AD的垂直平分线,由勾股定理得AB=10,进而可得AF=2.
【解答】解:由题意得,BC=BD=6,直线MN为线段AD的垂直平分线,
∵BC=6,AC=8,∠C=90°,
∴AB10,
∴AD=AB﹣BD=4,
∴AF2,
故答案为:2.
【点评】本题考查作图﹣基本作图、勾股定理、线段垂直平分线、相似三角形的判定与性质,熟练掌握相关知识点是解答本题的关键.
三.解答题(共5小题)
11.(2024秋 沙河口区期末)如图,线段AB,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于点M,N两点,作直线MN,点C在直线MN上,连接CA,CB,延长AC至点D.请根据要求完成以下作图与证明.
(1)用尺规完成以下基本作图:
作∠BCD的角平分线CE(保留作图痕迹,不写作法);
(2)在(1)所作的图中,求证:CE∥AB.
【考点】作图—复杂作图;平行线的判定;线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;尺规作图;几何直观.
【答案】(1)见解答.
(2)见解答.
【分析】(1)根据角平分线的作图方法作图即可.
(2)由作图过程可知,直线MN为线段AB的垂直平分线,可得CA=CB,则∠A=∠B,进而可得∠BCD=2∠B,即.由角平分线的定义可得,则∠B=∠BCE,即CE∥AB.
【解答】(1)解:如图,射线CE即为所求.
(2)证明:由作图过程可知,直线MN为线段AB的垂直平分线,
∴CA=CB,
∴∠A=∠B.
∵∠BCD=∠A+∠B,
∴∠BCD=2∠B,
即.
∵CE平分∠BCD,
∴,
∴∠B=∠BCE.
∴CE∥AB.
【点评】本题考查作图—复杂作图、平行线的判定、线段垂直平分线的性质,熟练掌握平行线的判定、线段垂直平分线的性质是解答本题的关键.
12.(2024秋 南岸区期末)已知:∠ABC=α,∠CBD=90°,用尺规完成下列作图,并回答问题.
(1)求作:以点B为顶点;射线BC为一边,在∠ABC外作∠CBE,使∠CBE=∠ABC;(不写作法,保留作图痕迹)
(2)延长AB至F,用等式表示图中所有相等的角,以及和为90°的角.
【考点】作图—基本作图;余角和补角.
【专题】几何直观.
【答案】(1)见解析;
(2)见解析.
【分析】(1)根据作一个角等于已知角的方法,作图即可;
(2)根据图形,结合∠ABC=∠CBE,同角或等角的余角相等,进行判断解答即可.
【解答】解:(1)如图所示,∠CBE即为所求作;
(2)相等的角有:∠ABC=∠CBE,∠EBD=∠FBD;
和为90°的角有:∠ABC+∠DBE=90°,∠ABC+∠FBD=90°,∠CBE+∠EBD=90°,∠CBE+∠FBD=90°.
【点评】本题主要考查作一个角等于已知角,余角的性质,解题的关键是熟练掌握作一个角等于已知角的方法.
13.(2024秋 大足区期末)如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(﹣1,5),B(﹣2,0),C(﹣4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
【考点】作图﹣轴对称变换.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)根据网格结构找出点A、B、C关于y轴对称的点A1、B1、C1的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标即可;
(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
【解答】解:(1)△A1B1C1如图所示;
(2)A1(1,5)B1(2,0)C1(4,3);
(3)△A1B1C1的面积=3×51×52×32×3,
=15﹣2.5﹣3﹣3,
=15﹣8.5,
=6.5.
【点评】本题考查了利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
14.(2024秋 平潭县期末)如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)作线段AB的垂直平分线即可;
(2)根据线段垂直平分线的性质可得BP=AP,根据等边对等角可得∠B=∠PAB,然后再根据角平分线定义可得∠CAP=∠PAB,进而可得∠B=∠PAB=∠CAP,然后可得答案.
【解答】解:(1)如图,点P为所作;
(2)∵点P在AB的垂直平分线MN上
∴PA=PB,
∴∠B=∠PAB,
∵AP平分∠CAB,
∴∠PAB∠CAB,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
即2∠B+∠B=90°,
∴∠B=30°.
【点评】此题主要考查了基本作图,以及线段垂直平分线的性质,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
15.(2024秋 泰兴市期末)如图,∠ACD是△ABC的一个外角.
(1)利用无刻度的直尺和圆规作图:在∠ACD的内部画射线CE,使CE∥AB(不写作法,保留作图痕迹);
(2)在(1)的条件下,若射线CE是∠ACD的平分线,∠B=54°,求∠A的度数.
【考点】作图—复杂作图;平行线的判定与性质.
【专题】尺规作图;几何直观.
【答案】(1)作图见解析;
(2)54°.
【分析】(1)作∠DCE=∠B即可得到CE∥AB;
(2)由CE∥AB可得∠B=∠DCE=54°,∠A=∠ACE,再结合角平分线的定义可得答案.
【解答】解:(1)如图,CE即为所求;
(2)∵CE∥AB,
∴∠B=∠DCE=54°,∠A=∠ACE,
∵CE是∠ACD的平分线,
∴∠ACE=∠DCE,
∴∠A=∠B=54°.
【点评】本题考查作图﹣复杂作图,平行线的判定与性质,解答本题的关键是熟练掌握画一个角等于已知角的方法.
21世纪教育网(www.21cnjy.com)
