13.1.3 直观图的斜二测画法 练习(含详解)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.1.3 直观图的斜二测画法 练习(含详解)2024-2025学年高一数学苏教版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 218.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 15:25:50 | ||
图片预览


文档简介
13.1.3 直观图的斜二测画法
一、 单项选择题
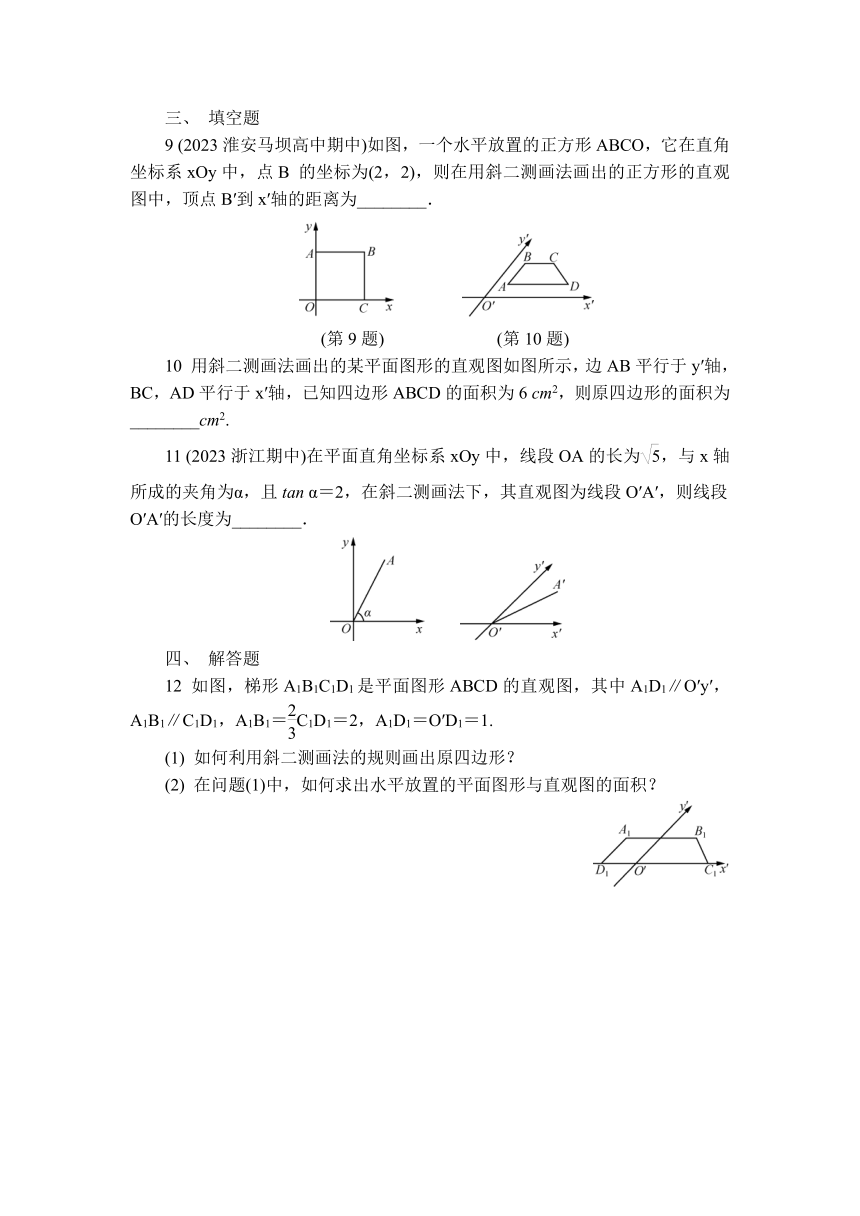
1 如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,A′B′∥y轴,且△ABO的面积为16,过点A′作A′C′⊥x′轴,则A′C′的长为 ( )
A. 2
B.
C. 16
D. 1
2 (2024芜湖期中)已知图2为甲同学用斜二测画法作出的在平面直角坐标系中正五边形ABCDE(如图1)的直观图,即五边形 A′B′C′D′E′,且保持坐标轴上的单位长度不变,其中各点的作法可能正确的为( )
图1 图2
A. A′,B′,P′ B. B′,P′,C′
C. P′,C′,D′ D. D′,E′,A′
3 (2024浙江期中)如图,直角梯形O′A′B′C′满足O′A′⊥O′C′,O′A′=A′B′=2,O′C′=3,它是水平放置的平面图形的直观图,则该平面图形的周长是( )
A. 7+ B. 5+2+
C. 11+ D. 10
4 (2024泰安期中)用斜二测画法画出的水平放置的平面图形△OAB的直观图为如图所示的△O′A′B′,已知△O′A′B′是边长为2的等边三角形,则顶点B到x轴的距离是( )
A. 2 B. 4 C. 2 D. 2
5 如图,水平放置的四边形ABCD的斜二测画法的直观图为矩形A′B′C′D′,已知A′O′=O′B′=1,B′C′=1,则四边形ABCD的周长为( )
A. 8 B. 10
C. 12 D. 4+2
(第5题) (第6题)
6 如图,△A′B′C′表示水平放置的△ABC根据斜二测画法得到的直观图,A′B′在x′轴上,B′C′与 x′轴垂直,且B′C′=2,则△ABC的边AB上的高为( )
A. B. 2 C. 4 D. 4
二、 多项选择题
7 如图是斜二测画法画出的水平放置的△ABC的直观图,D′为B′C′的中点,且 A′D′∥y′轴,B′C′∥x′轴,则在原平面图形△ABC中,下列结论中正确的是( )
A. AB=AC B. AD>AC
C. AB>AD D. BC>AD
(第7题) (第8题)
8 (2023济宁嘉祥县一中期中)如图,四边形ABCD的斜二测直观图为等腰梯形A′B′C′D′,已知A′B′=2C′D′=4,则下列结论中正确的是( )
A. A′D′=
B. BC=2
C. 四边形ABCD的周长为6+2+2
D. 四边形ABCD的面积为6
三、 填空题
9 (2023淮安马坝高中期中)如图,一个水平放置的正方形ABCO,它在直角坐标系xOy中,点B 的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为________.
(第9题) (第10题)
10 用斜二测画法画出的某平面图形的直观图如图所示,边AB平行于y′轴,BC,AD平行于x′轴,已知四边形ABCD的面积为6 cm2,则原四边形的面积为________cm2.
11 (2023浙江期中)在平面直角坐标系xOy中,线段OA的长为,与x轴所成的夹角为α,且tan α=2,在斜二测画法下,其直观图为线段O′A′,则线段O′A′的长度为________.
四、 解答题
12 如图,梯形A1B1C1D1是平面图形ABCD的直观图,其中A1D1∥O′y′,A1B1∥C1D1,A1B1=C1D1=2,A1D1=O′D1=1.
(1) 如何利用斜二测画法的规则画出原四边形?
(2) 在问题(1)中,如何求出水平放置的平面图形与直观图的面积?
13 已知一棱柱的底面是边长为3 cm的正方形,各侧面都是矩形,且侧棱长为 4 cm,试用斜二测画法画出此棱柱的直观图.
13.1.3 直观图的斜二测画法
1. A 因为A′B′∥y′轴,所以在△ABO中,AB⊥OB.又△ABO的面积为16,所以AB·OB=16,所以AB=8,所以A′B′=4.因为A′C′⊥x′轴,∠A′B′C′=45°,所以B′C′=A′C′,所以A′C′=4·sin 45°=2.
2. C 斜二侧画直观图时,平行或与x轴重合的线段长度不变,则CD,PQ长度不变, 平行或与 y轴重合的线段长度减半,则OA减掉一半,线段PB,PC,QE,QD对应线段也会缩小,如图,所以点P,C,D,Q的对应点P′,C′,D′,Q′可能画对了,点A,B,E的对应点A′,B′,E′画错了.
3. C 结合斜二测画法的规则,将直观图即直角梯形O′A′B′C′还原成平面图形,即四边形OABC,如图所示.由题意,得OC=O′C′=3,AB=A′B′=2,由A′B′∥O′C′,得AB∥OC,由O′A′⊥O′C′,∠B′O′C′=45°,A′B′∥O′C′,可得∠B′O′A′=∠A′B′O′=45°,所以∠O′A′B′=90°.又O′A′=A′B′=2,所以OB=2O′B′=2×=4,在△OBA中,由勾股定理,得AO==6.在△BOC中,由勾股定理,得BC==,所以满足题意的平面图形的周长是2+6+3+=11+.
4. A 如图,过点B′作B′B″∥y′轴交x′轴于点B″.在△B′B″O′中,O′B′=2,∠B′B″O′=45°,∠B′O′B″=120°,由正弦定理,得=,所以B′B″===.由斜二测画法可知,在原平面图形中,点B到x轴的距离是2B′B″=2.
5. B 由题意知,原四边形中AB=CD=A′B′=C′D′=2,且AB∥CD,所以原四边形ABCD为平行四边形.因为O′C′=,所以原四边形中OC=2,可得AD=BC==3.综上,四边形ABCD的周长为AB+CD+AD+BC=10.
6. D 如图,过点C′作x′轴的平行线,交y′轴于点D′,过点D′作D′E⊥x′轴,垂足为E,则D′E=B′C′=2,O′D′=D′E=2.由斜二测画法规则知点D′在原图中对应的点D在y轴上,且OD=2O′D′=4,即△ABC的边AB上的高为4.
7. AC 在直观图中,A′D′∥y′轴,根据斜二测画法规则,在△ABC中有AD⊥BC. 又AD为边BC上的中线,所以△ABC为等腰三角形,则AB=AC,且AB=AC>AD,但BC与AD的长度不确定.故选AC.
8. ACD 在等腰梯形A′B′C′D′中,∠D′A′B′=45°,A′B′=2C′D′=4,所以A′D′=.由斜二测画法可知,在原图直角梯形ABCD中,AB=2CD=4,AD=2,∠BAD=,易得BC=2,所以四边形ABCD的周长为6+2+2,面积为×(2+4)×2=6.故选ACD.
9. 如图,B′C′=BC=1,所以点B′到x′轴的距离为1×sin 45°=.
10. 12 由题意,得∠BAD=45°,原四边形为一个直角梯形,且上、下底的边长分别和BC,AD相等,高为AB的2倍,即为四边形ABCD的高的2倍,面积是四边形ABCD面积的2倍,故原平面图形的面积为6×2=12(cm2).
11. 如图1,过点A分别作x轴与y轴的垂线,交x轴与y轴于点B,C,在Rt△ABO中,OA=,tan ∠AOB=tan α==2,所以AB=2OB.又OB2+AB2=OA2,所以OB=1,AB=2,故OC=AB=2.如图2,过点A′分别作y′轴与x′轴的平行线,交x′轴与y′轴于B′,C′两点,则四边形O′B′A′C′为平行四边形,所以O′C′=A′B′,由平面直观图的性质知,O′B′=OB=1,O′C′=OC=1,所以A′B′=1.又因为∠x′O′y′=45°,所以∠O′B′A′=135°,在△O′B′A′中,由余弦定理,得O′A′2=O′B′2+A′B′2-2O′B′·A′B′cos ∠O′B′A′=1+1-2cos 135°=2+,所以O′A′=.
图1 图2
12. (1) 如图,建立平面直角坐标系xOy,在x轴上截取OD=O′D1=1,OC=O′C1=2.
在过点D的y轴的平行线上截取DA=2D1A1=2.在过点A的x轴的平行线上截取AB=A1B1=2.连接BC,即得到原四边形.
(2) 由(1)可知,原四边形ABCD是直角梯形,且AB=2,CD=3,AD=2,
所以面积为S=×2=5.
易得直观图中梯形的高为,
所以直观图的面积为S′=×(2+3)×=.
13. ①画轴.画出x轴,y轴,z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.
②画底面.以O为中点,在x轴上截取MN=3 cm,在y轴上截取PQ= cm,分别过点M,N作y轴的平行线,过点P,Q作x轴的平行线,设它们的交点分别为A,B,C,D,则四边形ABCD就是该棱柱的底面.
③画侧棱.过点A,B,C,D分别作z轴的平行线,并在这些平行线上分别截取4 cm长的线段AA′,BB′,CC′,DD′,如图1所示.
④成图. 连接A′B′,B′C′,C′D′,D′A′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到该棱柱的直观图,如图2所示.
图1 图2
一、 单项选择题
1 如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,A′B′∥y轴,且△ABO的面积为16,过点A′作A′C′⊥x′轴,则A′C′的长为 ( )
A. 2
B.
C. 16
D. 1
2 (2024芜湖期中)已知图2为甲同学用斜二测画法作出的在平面直角坐标系中正五边形ABCDE(如图1)的直观图,即五边形 A′B′C′D′E′,且保持坐标轴上的单位长度不变,其中各点的作法可能正确的为( )
图1 图2
A. A′,B′,P′ B. B′,P′,C′
C. P′,C′,D′ D. D′,E′,A′
3 (2024浙江期中)如图,直角梯形O′A′B′C′满足O′A′⊥O′C′,O′A′=A′B′=2,O′C′=3,它是水平放置的平面图形的直观图,则该平面图形的周长是( )
A. 7+ B. 5+2+
C. 11+ D. 10
4 (2024泰安期中)用斜二测画法画出的水平放置的平面图形△OAB的直观图为如图所示的△O′A′B′,已知△O′A′B′是边长为2的等边三角形,则顶点B到x轴的距离是( )
A. 2 B. 4 C. 2 D. 2
5 如图,水平放置的四边形ABCD的斜二测画法的直观图为矩形A′B′C′D′,已知A′O′=O′B′=1,B′C′=1,则四边形ABCD的周长为( )
A. 8 B. 10
C. 12 D. 4+2
(第5题) (第6题)
6 如图,△A′B′C′表示水平放置的△ABC根据斜二测画法得到的直观图,A′B′在x′轴上,B′C′与 x′轴垂直,且B′C′=2,则△ABC的边AB上的高为( )
A. B. 2 C. 4 D. 4
二、 多项选择题
7 如图是斜二测画法画出的水平放置的△ABC的直观图,D′为B′C′的中点,且 A′D′∥y′轴,B′C′∥x′轴,则在原平面图形△ABC中,下列结论中正确的是( )
A. AB=AC B. AD>AC
C. AB>AD D. BC>AD
(第7题) (第8题)
8 (2023济宁嘉祥县一中期中)如图,四边形ABCD的斜二测直观图为等腰梯形A′B′C′D′,已知A′B′=2C′D′=4,则下列结论中正确的是( )
A. A′D′=
B. BC=2
C. 四边形ABCD的周长为6+2+2
D. 四边形ABCD的面积为6
三、 填空题
9 (2023淮安马坝高中期中)如图,一个水平放置的正方形ABCO,它在直角坐标系xOy中,点B 的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为________.
(第9题) (第10题)
10 用斜二测画法画出的某平面图形的直观图如图所示,边AB平行于y′轴,BC,AD平行于x′轴,已知四边形ABCD的面积为6 cm2,则原四边形的面积为________cm2.
11 (2023浙江期中)在平面直角坐标系xOy中,线段OA的长为,与x轴所成的夹角为α,且tan α=2,在斜二测画法下,其直观图为线段O′A′,则线段O′A′的长度为________.
四、 解答题
12 如图,梯形A1B1C1D1是平面图形ABCD的直观图,其中A1D1∥O′y′,A1B1∥C1D1,A1B1=C1D1=2,A1D1=O′D1=1.
(1) 如何利用斜二测画法的规则画出原四边形?
(2) 在问题(1)中,如何求出水平放置的平面图形与直观图的面积?
13 已知一棱柱的底面是边长为3 cm的正方形,各侧面都是矩形,且侧棱长为 4 cm,试用斜二测画法画出此棱柱的直观图.
13.1.3 直观图的斜二测画法
1. A 因为A′B′∥y′轴,所以在△ABO中,AB⊥OB.又△ABO的面积为16,所以AB·OB=16,所以AB=8,所以A′B′=4.因为A′C′⊥x′轴,∠A′B′C′=45°,所以B′C′=A′C′,所以A′C′=4·sin 45°=2.
2. C 斜二侧画直观图时,平行或与x轴重合的线段长度不变,则CD,PQ长度不变, 平行或与 y轴重合的线段长度减半,则OA减掉一半,线段PB,PC,QE,QD对应线段也会缩小,如图,所以点P,C,D,Q的对应点P′,C′,D′,Q′可能画对了,点A,B,E的对应点A′,B′,E′画错了.
3. C 结合斜二测画法的规则,将直观图即直角梯形O′A′B′C′还原成平面图形,即四边形OABC,如图所示.由题意,得OC=O′C′=3,AB=A′B′=2,由A′B′∥O′C′,得AB∥OC,由O′A′⊥O′C′,∠B′O′C′=45°,A′B′∥O′C′,可得∠B′O′A′=∠A′B′O′=45°,所以∠O′A′B′=90°.又O′A′=A′B′=2,所以OB=2O′B′=2×=4,在△OBA中,由勾股定理,得AO==6.在△BOC中,由勾股定理,得BC==,所以满足题意的平面图形的周长是2+6+3+=11+.
4. A 如图,过点B′作B′B″∥y′轴交x′轴于点B″.在△B′B″O′中,O′B′=2,∠B′B″O′=45°,∠B′O′B″=120°,由正弦定理,得=,所以B′B″===.由斜二测画法可知,在原平面图形中,点B到x轴的距离是2B′B″=2.
5. B 由题意知,原四边形中AB=CD=A′B′=C′D′=2,且AB∥CD,所以原四边形ABCD为平行四边形.因为O′C′=,所以原四边形中OC=2,可得AD=BC==3.综上,四边形ABCD的周长为AB+CD+AD+BC=10.
6. D 如图,过点C′作x′轴的平行线,交y′轴于点D′,过点D′作D′E⊥x′轴,垂足为E,则D′E=B′C′=2,O′D′=D′E=2.由斜二测画法规则知点D′在原图中对应的点D在y轴上,且OD=2O′D′=4,即△ABC的边AB上的高为4.
7. AC 在直观图中,A′D′∥y′轴,根据斜二测画法规则,在△ABC中有AD⊥BC. 又AD为边BC上的中线,所以△ABC为等腰三角形,则AB=AC,且AB=AC>AD,但BC与AD的长度不确定.故选AC.
8. ACD 在等腰梯形A′B′C′D′中,∠D′A′B′=45°,A′B′=2C′D′=4,所以A′D′=.由斜二测画法可知,在原图直角梯形ABCD中,AB=2CD=4,AD=2,∠BAD=,易得BC=2,所以四边形ABCD的周长为6+2+2,面积为×(2+4)×2=6.故选ACD.
9. 如图,B′C′=BC=1,所以点B′到x′轴的距离为1×sin 45°=.
10. 12 由题意,得∠BAD=45°,原四边形为一个直角梯形,且上、下底的边长分别和BC,AD相等,高为AB的2倍,即为四边形ABCD的高的2倍,面积是四边形ABCD面积的2倍,故原平面图形的面积为6×2=12(cm2).
11. 如图1,过点A分别作x轴与y轴的垂线,交x轴与y轴于点B,C,在Rt△ABO中,OA=,tan ∠AOB=tan α==2,所以AB=2OB.又OB2+AB2=OA2,所以OB=1,AB=2,故OC=AB=2.如图2,过点A′分别作y′轴与x′轴的平行线,交x′轴与y′轴于B′,C′两点,则四边形O′B′A′C′为平行四边形,所以O′C′=A′B′,由平面直观图的性质知,O′B′=OB=1,O′C′=OC=1,所以A′B′=1.又因为∠x′O′y′=45°,所以∠O′B′A′=135°,在△O′B′A′中,由余弦定理,得O′A′2=O′B′2+A′B′2-2O′B′·A′B′cos ∠O′B′A′=1+1-2cos 135°=2+,所以O′A′=.
图1 图2
12. (1) 如图,建立平面直角坐标系xOy,在x轴上截取OD=O′D1=1,OC=O′C1=2.
在过点D的y轴的平行线上截取DA=2D1A1=2.在过点A的x轴的平行线上截取AB=A1B1=2.连接BC,即得到原四边形.
(2) 由(1)可知,原四边形ABCD是直角梯形,且AB=2,CD=3,AD=2,
所以面积为S=×2=5.
易得直观图中梯形的高为,
所以直观图的面积为S′=×(2+3)×=.
13. ①画轴.画出x轴,y轴,z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.
②画底面.以O为中点,在x轴上截取MN=3 cm,在y轴上截取PQ= cm,分别过点M,N作y轴的平行线,过点P,Q作x轴的平行线,设它们的交点分别为A,B,C,D,则四边形ABCD就是该棱柱的底面.
③画侧棱.过点A,B,C,D分别作z轴的平行线,并在这些平行线上分别截取4 cm长的线段AA′,BB′,CC′,DD′,如图1所示.
④成图. 连接A′B′,B′C′,C′D′,D′A′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到该棱柱的直观图,如图2所示.
图1 图2
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
