13.2.3 直线与平面的位置关系——直线与平面平行 练习(2课时,含详解)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.2.3 直线与平面的位置关系——直线与平面平行 练习(2课时,含详解)2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 530.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 15:32:44 | ||
图片预览




文档简介
13.2.3 直线与平面的位置关系——直线与平面平行(1)
一、 单项选择题
1 (2024周口月考)已知直线a与平面α没有公共点,直线b α,则a与b的位置关系是( )
A. 平行 B. 异面
C. 相交 D. 平行或异面
2 (2023滨州期中)设a,b是两条不同的直线,α是平面,b α,则“a∥b”是“a∥α”的( )
A. 充分且不必要条件
B. 必要且不充分条件
C. 充要条件
D. 既不充分又不必要条件
3 (2024沧州期中)下列命题中,正确的是( )
A. 若直线l上有无数个点不在平面α内,则l∥α
B. 若直线l与平面α平行,则平面α内有无数条直线与l平行
C. 若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行
D. 若直线l与平面α平行,则l与平面α内的任意一条直线都平行
4 (2024连云港期中)在空间四边形ABCD中,H,G分别为BC,CD的中点,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶2,则下列结论中正确的是( )
A. BD∥平面EFGH且四边形EFGH为矩形
B. HG∥平面ABD且四边形EFGH为菱形
C. HE∥平面ADC且四边形EFGH为平行四边形
D. EF∥平面BCD且四边形EFGH为梯形
5 (2023石家庄新乐一中期中)在长方体ABCD-A1B1C1D1中,若M为A1B1的中点,则下列说法中正确的是( )
A. BC1∥平面D1MC
B. C1D1∥平面ACM
C. CM∥平面A1BD
D. B1C∥平面D1MB
6 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器中灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有以下结论:①水的形状始终呈棱柱形;②水面EFGH的面积不变;③A1D1始终与水面EFGH平行.其中正确结论的序号为( )
A. ①② B. ①③ C. ②③ D. ①②③
二、 多项选择题
7 (2023邯郸大名县一中期中)已知a,b表示直线,α表示平面,则下列命题中是假命题的是( )
A. 若a∥b,b α,则a∥α
B. 若a∥α,b∥α,则a∥b
C. 若a∥b,b∥α,则a∥α
D. 若a∥α,b α,则a∥b或a与b异面
8 (2024佛山期中)在正方体ABCD-A1B1C1D1中,M,N,P分别是AA1,CC1,C1D1的中点,Q是线段D1A1上异于端点的动点,则下列说法中正确的是( )
A. 直线MP与直线BN是异面直线
B. 直线MN与直线BP是相交直线
C. 存在点Q,使B,N,P,Q四点共面
D. 存在点Q,使PQ∥平面MBN
三、 填空题
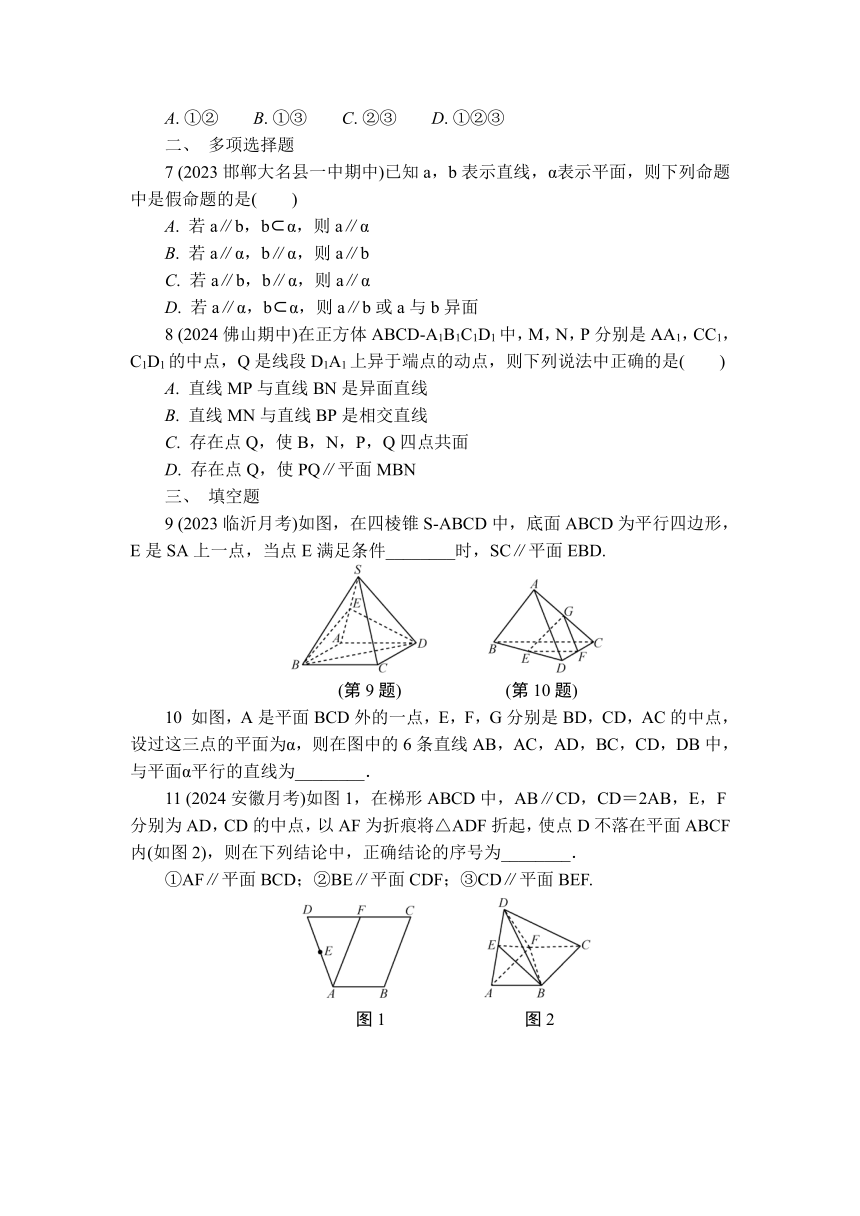
9 (2023临沂月考)如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA上一点,当点E满足条件________时,SC∥平面EBD.
(第9题) (第10题)
10 如图,A是平面BCD外的一点,E,F,G分别是BD,CD,AC的中点,设过这三点的平面为α,则在图中的6条直线AB,AC,AD,BC,CD,DB中,与平面α平行的直线为________.
11 (2024安徽月考)如图1,在梯形ABCD中,AB∥CD,CD=2AB,E,F分别为AD,CD的中点,以AF为折痕将△ADF折起,使点D不落在平面ABCF内(如图2),则在下列结论中,正确结论的序号为________.
①AF∥平面BCD;②BE∥平面CDF;③CD∥平面BEF.
图1 图2
四、 解答题
12 已知四棱锥P-ABCD的底面ABCD是梯形,AB∥DC,∠BAD=90°,AB=AD=2,DC=3,点E在棱PC上,且PE=2EC.求证:BE∥平面PAD.
13 (2023广东期中)如图,在棱长为2的正方体ABCD-A1B1C1D1中,P,Q分别是棱DD1,AB的中点.
(1) 设平面PQC与直线AA1交于点R,求的值;
(2) 在线段CC1上是否存在点M,使得BM∥平面PQC?若存在,求出点M的位置并证明;若不存在,请说明理由.
13.2.3 直线与平面的位置关系——直线与平面平行(2)
一、 单项选择题
1 (2024福建月考)下列说法中,正确的是( )
A. 若直线l平行于平面α内的无数条直线,则l∥α
B. 若直线a在平面α外,则a∥α
C. 若直线a∥b,b α,则a∥α
D. 若直线a∥b,b α,则直线a就平行于平面内的无数条直线
2 如图,四边形ABDC是梯形,AB∥CD,且AB∥平面α,M是AC的中点,BD与平面α交于点N,AB=4,CD=6,则MN等于( )
A. 4.5 B. 5
C. 5.4 D. 5.5
(第2题) (第3题)
3 (2024烟台月考)如图,在三棱台ABC-A1B1C1中,从A,B,C,A1,B1,C1中取3个点确定平面α,若平面α∩平面A1B1C1=m,且m∥AB,则所取的这3个点可以是( )
A. A1,B,C B. A1,B,C1
C. A,B,C1 D. A,B1,C1
4 (2023洛阳期中)如图,已知圆锥的顶点为S,AB为底面圆的直径,M,C为底面圆周上的点,且将弧AB三等分.过AC作平面α,使SB∥α,设α与SM交于点N,则 的值为( )
A. B.
C. D.
5 在棱长为2的正方体ABCD-A1B1C1D1中,过A1B且与AC1平行的平面交B1C1于点P,则PC1的长为( )
A. 2 B. C. D. 1
6 (2023渭南期末)一平面截空间四边形的四边得到四个交点,如果该空间四边形只有一条对角线与这个截面平行,那么这四个交点围成的四边形是( )
A. 梯形 B. 菱形
C. 平行四边形 D. 任意四边形
二、 多项选择题
7 (2024安徽月考)若直线a平行于平面α,则下列结论中正确的是( )
A. 平面α内有且只有一条直线与a平行
B. 平面α内有无数条直线与a平行
C. 平面α内存在无数条与a不平行的直线
D. 平面α内任意一条直线都与a平行
8 (2024南昌开学考试)在下列底面为平行四边形的四棱锥中,M,S,T,P,Q是四棱锥的顶点或棱的中点(如图),则PQ∥平面MST的有( )
A B C D
三、 填空题
9 如图,三棱柱ABC-A1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且A1B∥平面B1CD,则的值为________.
10 在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,P是棱AD上的一点,且AP=,过点P,M,N的平面与棱CD交于点Q,则PQ=________.
11 (2024巴中期末)如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上,若EF∥平面AB1C,则EF=________.
四、 解答题
12 (2024广州期中)如图,P为平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点.
(1) 求证:MN∥平面PAD;
(2) 若平面PAD∩平面PBC=l,判断BC与l的位置关系,并证明你的结论.
13 (2024浙江期中)如图,在多面体ABCDFE中,四边形ABCD为直角梯形,DC=2AB,GC=2FG,平面ABFE∩平面CDEF=EF.求证:
(1) AF∥平面BDG;
(2) AB∥EF.
13.2.3 直线与平面的位置关系
——直线与平面平行(1)
1. D 依题意可知a∥α.因为b α,所以a,b没有公共点,则a与b可能异面或平行.
2. D 由线面平行的判定定理,a∥b,b α,a α,方可推出a∥α,故“a∥b”不是“a∥α”的充分条件;若a∥α,则可在平面α内找到一条直线与a平行,不一定有a∥b,故“a∥b”不是“a∥α”的必要条件.综上,“a∥b”是“a∥α”的既不充分又不必要条件.
3. B 对于A,若直线l上有无数个点不在平面α内,则l∥α或l与α相交,故A错误;对于B,直线l与平面α平行,则存在过直线l的平面与平面α相交,令交线为c,则l∥c,显然在平面α内有无数条直线与c平行,这些直线都平行于l,故B正确;对于C,若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行或在这个平面内,故C错误;对于D,若直线l与平面α平行,则l与平面α内的直线平行或是异面直线,不会与平面α内的任意一条直线都平行,故D错误.
4. D 因为H,G分别为BC,CD的中点,所以HG∥BD且HG=BD.因为E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶2,所以EF∥BD且EF=BD,所以EF∥HG且EF≠HG,所以四边形EFGH为梯形.又EF 平面BCD,BD 平面BCD,所以EF∥平面BCD.
5. D 对于A,如图1,取BB1的中点N,连接MN,NC,A1B.又M为A1B1的中点,所以 MN∥A1B,根据长方体的对称性可知A1B∥D1C,所以MN∥D1C,所以M,N,C,D1四点共面,直线 BC1与NC相交,所以BC1与平面MNCD1相交,故A错误;对于B,如图2,取B1C1的中点E,连接ME,CE.由选项A同理可证,ME∥AC,所以M,E,C,A四点共面,在平面A1B1C1D1内,直线D1C1与ME相交,所以C1D1与平面MACE相交,故B错误;对于C,如图3,连接B1C.在平面A1DCB1内,直线A1D与CM相交,所以CM与平面A1BD相交,故C错误;对于D,如图4,取DC的中点F,连接D1F,BF,MF,A1D.由长方体的对称性,易得BF∥D1M,所以D1,F,B,M四点共面,在平面A1DCB1内,直线MF∥B1C,B1C 平面D1MB,MF 平面D1MB,所以B1C∥平面D1MB,故D正确.
图1 图2 图3 图4
6. B 当长方体容器绕BC边转动时,盛水部分的空间图形始终满足棱柱定义,故①正确;在转动过程中EH∥FG,但EH与FG的距离EF在变,所以水面EFGH的面积在变化,故②错误;在转动过程中,始终有A1D1∥平面EFGH,故③正确.
7. ABC 如图为正方体ABCD-A1B1C1D1.对于A,A1B1∥AB,AB 平面ABB1A1,A1B1 平面ABB1A1,故A为假命题;对于B,A1B1∥平面ABCD,B1C1∥平面ABCD,但A1B1与B1C1相交,故B为假命题;对于C,AB∥CD,CD∥平面ABB1A1,AB 平面ABB1A1,故C为假命题;对于D,因为a∥α,所以a与α无公共点.又b在α内,所以a与b无公共点,所以a∥b或a与b异面,故D为真命题.故选ABC.
8. AD 如图,连接MD1,D1N.由M,N分别是AA1,CC1的中点,可得BN∥MD1,所以B,N,D1,M四点共面.又平面BND1M∩平面CDD1C1=ND1,P∈平面CDD1C1,P 直线ND1,所以P 平面BND1M,故点P与B,N,M三点不共面,所以直线MP与直线BN是异面直线,直线MN与直线BP是异面直线,故A正确,B错误;因为P是C1D1的中点,所以PN∥D1C∥A1B,故B,N,P三点确定平面PNBA1,所以平面PNBA1与直线A1D1仅有一个公共点A1,但点Q不与点A1重合,故不存在点Q使得Q∈平面PNBA1,故C错误;由选项A知P 平面MBN,故PQ 平面MBN,只需Q为A1D1的中点,则有PQ∥A1C1∥MN,所以PQ∥平面MBN,故D正确.故选AD.
9. SE=AE 如图,连接AC交BD于点O,连接OE.因为SC∥平面EBD,SC 平面SAC,平面SAC∩平面 EBD=OE,所以SC∥OE.又因为底面ABCD为平行四边形,O为对角线AC与BD的交点,故O为AC的中点,所以E为SA的中点,故当点E满足条件SE=AE 时,SC∥平面EBD.
10. AD,BC 显然AB,AC,DB,CD四条直线均与平面α相交.在△BCD中,由已知得EF∥BC,又EF α,BC α,所以BC∥α.同理,AD∥α,所以在题图中的6条直线中,与平面α平行的直线为AD,BC.
11. ①③ 对于①,由题意,得AB∥CF,AB=CF,所以四边形ABCF是平行四边形,所以AF∥BC.因为AF 平面BCD,BC 平面BCD,所以AF∥平面BCD,故①正确;对于②,如图,取DF的中点G,连接EG,CG.因为E是AD的中点,AF∥BC,AF=BC,所以EG=BC,EG∥BC,所以四边形BCGE为梯形,所以直线BE与直线CG相交,所以BE与平面CDF相交,故②错误;对于③,如图,连接AC,交BF于点O,连接OE.因为四边形ABCF是平行四边形,所以O是AC的中点,所以OE∥CD.因为OE 平面BEF,CD 平面BEF,所以CD∥平面BEF,故③正确.故正确结论的序号为①③.
12. 作EF∥DC交PD于点F,连接AF.
因为点E在棱PC上,且PE=2EC,所以FE=DC=2.
因为AB∥DC,AB=2,所以AB∥FE,且AB=FE,
所以四边形ABEF为平行四边形,则AF∥BE.
因为BE 平面PAD,AF 平面PAD,
所以BE∥平面PAD.
13. (1) 如图1,延长CQ和DA交于点E,连接PE,交AA1于点R,
即平面PQC与直线AA1交于点R.
因为Q为AB的中点,AQ∥DC,所以A为ED的中点,
所以AR=PD=DD1=AA1,所以=.
(2) 存在,当M为线段CC1上靠近点C的四等分点时,BM∥平面PQC,证明如下:
如图2,取PC的中点N,DC的中点G,连接NG,NM,则MN∥GC,且MN=GC,所以MN∥BQ,且MN=BQ,
所以四边形MNQB为平行四边形,
所以BM∥NQ.
又因为BM 平面PQC,NQ 平面PQC,
所以BM∥平面PQC.
图1 图2
13.2.3 直线与平面的位置关系
——直线与平面平行(2)
1. D 对于A,若直线l平行于平面α内的无数条直线,当这无数条直线是平行线时,l可能在平面内,与α不一定平行,故A不正确;对于B,若直线a在平面α外,则a∥α或a与α相交,故B不正确;对于C,若直线a∥b,b α,则a∥α或a α,故C不正确;对于D,若直线a∥b,b α,则a∥α或a α,所以a平行于平面α内的无数条直线,故D正确.
2. B 因为AB∥平面α,AB 平面ABDC,平面ABDC∩平面α=MN,所以AB∥MN. 又M是AC的中点,所以MN是梯形ABDC的中位线,故MN=(AB+CD)=5.
3. C 因为多面体A1B1C1-ABC是三棱台,所以AB∥A1B1.又AB 平面A1B1C1,A1B1 平面A1B1C1,所以AB∥平面A1B1C1,当AB 平面α,平面α∩平面A1B1C1=m时,由直线与平面平行的性质定理可知m∥AB,故选项C符合要求.
4. C 如图,连接MB交AC于点D,连接DN,NA,NC,MC,则平面NAC即为平面α.因为SB∥α,SB 平面SMB,平面SMB∩α=DN,所以SB∥DN.因为AB为底面圆的直径,点M,C将弧AB三等分,所以∠ABM=∠BMC=∠MBC=∠BAC=30°,MC=BC=AB,所以MC∥AB且MC=AB,所以==.又SB∥DN,所以==,所以=.
5. D 如图,连接AB1交A1B于点O,过点O作OP∥AC1交B1C1于点P,连接A1P,BP. 因为OP 平面A1PB,AC1 平面A1PB,所以AC1∥平面A1PB,即此时点P满足题意. 在△AB1C1中,==.又B1C1=2,所以PC1=1.
6. A 根据题意,不妨设该平面截空间四边形ABCD的四边得到四个交点E,F,G,H,AC∥平面EFGH,BD不平行于平面EFGH.因为AC∥平面EFGH,AC 平面ABC,且平面ABC∩平面EFGH=EF,所以AC∥EF,同理可得AC∥GH,所以GH∥EF.下面证明EH与FG不平行,假设EH∥FG,由FG 平面BCD,EH 平面BCD,得EH∥平面BCD.又因为EH 平面ABD,且平面ABD∩平面BCD=BD,由线面平行的性质定理可得EH∥BD.又EH 平面EFGH,BD 平面EFGH,所以BD∥平面EFGH,与题设BD不平行于平面EFGH矛盾,所以EH与FG不平行,所以四边形EFGH是梯形.
7. BC 过直线a可作无数个平面与α相交,由线面平行的性质定理可知,这些交线都与a平行,所以在平面α内与直线a平行的直线有无数条,故A不正确,B正确;若直线a平行于平面α,则直线a与平面α内的直线有两种位置关系:平行或异面,所以平面α内存在与a不平行的直线,且有无数条,故C正确,D不正确.故选BC.
8. AB 对于A,如图1,设A为MS的中点,底面为平行四边形STFE,连接PA,TA,则PA∥SE,PA=SE.又TQ∥SE,TQ=SE,所以PA∥TQ,PA=TQ,即四边形PATQ为平行四边形,所以PQ∥AT.又AT 平面MTS,PQ 平面MTS,所以PQ∥平面MST,故A正确;对于B,如图2,设A为MS的中点,底面为平行四边形STFE,连接PA,AT,则AP∥ES,AP=ES.又QT∥ES,QT=ES,故AP∥QT,AP=QT,即四边形APQT为平行四边形,所以PQ∥AT.又AT 平面MST,PQ 平面MST,所以PQ∥平面MST,故B正确;对于C,如图3,设A为ME的中点,底面为平行四边形GFES,连接QA,AS,设AQ交MT于点H,连接SH,则AQ∥FE,AQ=FE.又PS∥EF,PS=EF,所以AQ∥PS,AQ=PS,所以四边形AQPS为平行四边形,所以AS∥PQ.又PQ 平面AQPS,PQ 平面MST,平面AQPS∩平面MST=SH,假设PQ∥平面MST,则PQ∥SH,即在平面AQPS内过点S有两条直线和PQ都平行,这是不可能的,故C错误;对于D,如图4,设底面为平行四边形MQEF,连接ME,FQ交于点H,连接FQ,MT交于点G,则H为FQ的中点,连接SH,SG.因为S为PF的中点,所以SH∥PQ.又PQ 平面PFQ,PQ 平面MST,平面PFQ∩平面MST=SG,假设PQ∥平面MST,则PQ∥SG,即在平面PFQ内过点S有两条直线和PQ都平行,这是不可能的,故D错误.故选AB.
图1 图2 图3 图4
9. 1 因为A1B∥平面B1CD,A1B 平面A1BC1,平面A1BC1∩平面B1CD=OD,所以A1B∥OD.因为四边形BCC1B1是菱形,所以O为BC1的中点,所以D为A1C1的中点,即=1.
10. 因为A1C1∥AC,MN∥A1C1,所以MN∥AC. 由线面平行的判定定理和性质定理可知MN∥PQ,所以PQ∥AC,所以=,即=,即PQ=.
11. 因为EF∥平面AB1C,EF 平面ABCD,且平面ABCD∩平面AB1C=AC,所以EF∥AC.又E是AD的中点,所以F是CD的中点.因为在Rt△DEF中,DE=DF=1,所以EF=.
12. (1) 如图,取PD的中点E,连接AE,NE.
因为N,E分别为PC,PD的中点,
所以NE∥DC,且NE=DC.
又M为AB的中点,AB∥DC,AB=DC,
所以AM∥NE,且AM=NE,
所以四边形AMNE为平行四边形,
所以AE∥MN.
又AE 平面PAD,MN 平面PAD,
所以MN∥平面PAD.
(2) 因为四边形ABCD为平行四边形,
所以AD∥BC.
又BC 平面PAD,AD 平面PAD,
所以BC∥平面PAD.
又平面PAD∩平面PBC=l,BC 平面PBC,
所以BC∥l.
13. (1) 如图,连接AC交BD于点O,连接OG.
因为四边形ABCD为直角梯形,DC=2AB,
所以AB∥CD,所以==.
又因为GC=2FG,==,所以AF∥OG.
因为OG 平面BDG,AF 平面BDG,
所以AF∥平面BDG.
(2) 因为四边形ABCD为直角梯形,DC=2AB,
所以AB∥CD.
因为CD 平面CDEF,AB 平面CDEF,
所以AB∥平面CDEF.
因为AB 平面ABFE,平面CDEF∩平面ABFE=EF,
所以AB∥EF.
一、 单项选择题
1 (2024周口月考)已知直线a与平面α没有公共点,直线b α,则a与b的位置关系是( )
A. 平行 B. 异面
C. 相交 D. 平行或异面
2 (2023滨州期中)设a,b是两条不同的直线,α是平面,b α,则“a∥b”是“a∥α”的( )
A. 充分且不必要条件
B. 必要且不充分条件
C. 充要条件
D. 既不充分又不必要条件
3 (2024沧州期中)下列命题中,正确的是( )
A. 若直线l上有无数个点不在平面α内,则l∥α
B. 若直线l与平面α平行,则平面α内有无数条直线与l平行
C. 若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行
D. 若直线l与平面α平行,则l与平面α内的任意一条直线都平行
4 (2024连云港期中)在空间四边形ABCD中,H,G分别为BC,CD的中点,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶2,则下列结论中正确的是( )
A. BD∥平面EFGH且四边形EFGH为矩形
B. HG∥平面ABD且四边形EFGH为菱形
C. HE∥平面ADC且四边形EFGH为平行四边形
D. EF∥平面BCD且四边形EFGH为梯形
5 (2023石家庄新乐一中期中)在长方体ABCD-A1B1C1D1中,若M为A1B1的中点,则下列说法中正确的是( )
A. BC1∥平面D1MC
B. C1D1∥平面ACM
C. CM∥平面A1BD
D. B1C∥平面D1MB
6 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器中灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有以下结论:①水的形状始终呈棱柱形;②水面EFGH的面积不变;③A1D1始终与水面EFGH平行.其中正确结论的序号为( )
A. ①② B. ①③ C. ②③ D. ①②③
二、 多项选择题
7 (2023邯郸大名县一中期中)已知a,b表示直线,α表示平面,则下列命题中是假命题的是( )
A. 若a∥b,b α,则a∥α
B. 若a∥α,b∥α,则a∥b
C. 若a∥b,b∥α,则a∥α
D. 若a∥α,b α,则a∥b或a与b异面
8 (2024佛山期中)在正方体ABCD-A1B1C1D1中,M,N,P分别是AA1,CC1,C1D1的中点,Q是线段D1A1上异于端点的动点,则下列说法中正确的是( )
A. 直线MP与直线BN是异面直线
B. 直线MN与直线BP是相交直线
C. 存在点Q,使B,N,P,Q四点共面
D. 存在点Q,使PQ∥平面MBN
三、 填空题
9 (2023临沂月考)如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA上一点,当点E满足条件________时,SC∥平面EBD.
(第9题) (第10题)
10 如图,A是平面BCD外的一点,E,F,G分别是BD,CD,AC的中点,设过这三点的平面为α,则在图中的6条直线AB,AC,AD,BC,CD,DB中,与平面α平行的直线为________.
11 (2024安徽月考)如图1,在梯形ABCD中,AB∥CD,CD=2AB,E,F分别为AD,CD的中点,以AF为折痕将△ADF折起,使点D不落在平面ABCF内(如图2),则在下列结论中,正确结论的序号为________.
①AF∥平面BCD;②BE∥平面CDF;③CD∥平面BEF.
图1 图2
四、 解答题
12 已知四棱锥P-ABCD的底面ABCD是梯形,AB∥DC,∠BAD=90°,AB=AD=2,DC=3,点E在棱PC上,且PE=2EC.求证:BE∥平面PAD.
13 (2023广东期中)如图,在棱长为2的正方体ABCD-A1B1C1D1中,P,Q分别是棱DD1,AB的中点.
(1) 设平面PQC与直线AA1交于点R,求的值;
(2) 在线段CC1上是否存在点M,使得BM∥平面PQC?若存在,求出点M的位置并证明;若不存在,请说明理由.
13.2.3 直线与平面的位置关系——直线与平面平行(2)
一、 单项选择题
1 (2024福建月考)下列说法中,正确的是( )
A. 若直线l平行于平面α内的无数条直线,则l∥α
B. 若直线a在平面α外,则a∥α
C. 若直线a∥b,b α,则a∥α
D. 若直线a∥b,b α,则直线a就平行于平面内的无数条直线
2 如图,四边形ABDC是梯形,AB∥CD,且AB∥平面α,M是AC的中点,BD与平面α交于点N,AB=4,CD=6,则MN等于( )
A. 4.5 B. 5
C. 5.4 D. 5.5
(第2题) (第3题)
3 (2024烟台月考)如图,在三棱台ABC-A1B1C1中,从A,B,C,A1,B1,C1中取3个点确定平面α,若平面α∩平面A1B1C1=m,且m∥AB,则所取的这3个点可以是( )
A. A1,B,C B. A1,B,C1
C. A,B,C1 D. A,B1,C1
4 (2023洛阳期中)如图,已知圆锥的顶点为S,AB为底面圆的直径,M,C为底面圆周上的点,且将弧AB三等分.过AC作平面α,使SB∥α,设α与SM交于点N,则 的值为( )
A. B.
C. D.
5 在棱长为2的正方体ABCD-A1B1C1D1中,过A1B且与AC1平行的平面交B1C1于点P,则PC1的长为( )
A. 2 B. C. D. 1
6 (2023渭南期末)一平面截空间四边形的四边得到四个交点,如果该空间四边形只有一条对角线与这个截面平行,那么这四个交点围成的四边形是( )
A. 梯形 B. 菱形
C. 平行四边形 D. 任意四边形
二、 多项选择题
7 (2024安徽月考)若直线a平行于平面α,则下列结论中正确的是( )
A. 平面α内有且只有一条直线与a平行
B. 平面α内有无数条直线与a平行
C. 平面α内存在无数条与a不平行的直线
D. 平面α内任意一条直线都与a平行
8 (2024南昌开学考试)在下列底面为平行四边形的四棱锥中,M,S,T,P,Q是四棱锥的顶点或棱的中点(如图),则PQ∥平面MST的有( )
A B C D
三、 填空题
9 如图,三棱柱ABC-A1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且A1B∥平面B1CD,则的值为________.
10 在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,P是棱AD上的一点,且AP=,过点P,M,N的平面与棱CD交于点Q,则PQ=________.
11 (2024巴中期末)如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上,若EF∥平面AB1C,则EF=________.
四、 解答题
12 (2024广州期中)如图,P为平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点.
(1) 求证:MN∥平面PAD;
(2) 若平面PAD∩平面PBC=l,判断BC与l的位置关系,并证明你的结论.
13 (2024浙江期中)如图,在多面体ABCDFE中,四边形ABCD为直角梯形,DC=2AB,GC=2FG,平面ABFE∩平面CDEF=EF.求证:
(1) AF∥平面BDG;
(2) AB∥EF.
13.2.3 直线与平面的位置关系
——直线与平面平行(1)
1. D 依题意可知a∥α.因为b α,所以a,b没有公共点,则a与b可能异面或平行.
2. D 由线面平行的判定定理,a∥b,b α,a α,方可推出a∥α,故“a∥b”不是“a∥α”的充分条件;若a∥α,则可在平面α内找到一条直线与a平行,不一定有a∥b,故“a∥b”不是“a∥α”的必要条件.综上,“a∥b”是“a∥α”的既不充分又不必要条件.
3. B 对于A,若直线l上有无数个点不在平面α内,则l∥α或l与α相交,故A错误;对于B,直线l与平面α平行,则存在过直线l的平面与平面α相交,令交线为c,则l∥c,显然在平面α内有无数条直线与c平行,这些直线都平行于l,故B正确;对于C,若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行或在这个平面内,故C错误;对于D,若直线l与平面α平行,则l与平面α内的直线平行或是异面直线,不会与平面α内的任意一条直线都平行,故D错误.
4. D 因为H,G分别为BC,CD的中点,所以HG∥BD且HG=BD.因为E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶2,所以EF∥BD且EF=BD,所以EF∥HG且EF≠HG,所以四边形EFGH为梯形.又EF 平面BCD,BD 平面BCD,所以EF∥平面BCD.
5. D 对于A,如图1,取BB1的中点N,连接MN,NC,A1B.又M为A1B1的中点,所以 MN∥A1B,根据长方体的对称性可知A1B∥D1C,所以MN∥D1C,所以M,N,C,D1四点共面,直线 BC1与NC相交,所以BC1与平面MNCD1相交,故A错误;对于B,如图2,取B1C1的中点E,连接ME,CE.由选项A同理可证,ME∥AC,所以M,E,C,A四点共面,在平面A1B1C1D1内,直线D1C1与ME相交,所以C1D1与平面MACE相交,故B错误;对于C,如图3,连接B1C.在平面A1DCB1内,直线A1D与CM相交,所以CM与平面A1BD相交,故C错误;对于D,如图4,取DC的中点F,连接D1F,BF,MF,A1D.由长方体的对称性,易得BF∥D1M,所以D1,F,B,M四点共面,在平面A1DCB1内,直线MF∥B1C,B1C 平面D1MB,MF 平面D1MB,所以B1C∥平面D1MB,故D正确.
图1 图2 图3 图4
6. B 当长方体容器绕BC边转动时,盛水部分的空间图形始终满足棱柱定义,故①正确;在转动过程中EH∥FG,但EH与FG的距离EF在变,所以水面EFGH的面积在变化,故②错误;在转动过程中,始终有A1D1∥平面EFGH,故③正确.
7. ABC 如图为正方体ABCD-A1B1C1D1.对于A,A1B1∥AB,AB 平面ABB1A1,A1B1 平面ABB1A1,故A为假命题;对于B,A1B1∥平面ABCD,B1C1∥平面ABCD,但A1B1与B1C1相交,故B为假命题;对于C,AB∥CD,CD∥平面ABB1A1,AB 平面ABB1A1,故C为假命题;对于D,因为a∥α,所以a与α无公共点.又b在α内,所以a与b无公共点,所以a∥b或a与b异面,故D为真命题.故选ABC.
8. AD 如图,连接MD1,D1N.由M,N分别是AA1,CC1的中点,可得BN∥MD1,所以B,N,D1,M四点共面.又平面BND1M∩平面CDD1C1=ND1,P∈平面CDD1C1,P 直线ND1,所以P 平面BND1M,故点P与B,N,M三点不共面,所以直线MP与直线BN是异面直线,直线MN与直线BP是异面直线,故A正确,B错误;因为P是C1D1的中点,所以PN∥D1C∥A1B,故B,N,P三点确定平面PNBA1,所以平面PNBA1与直线A1D1仅有一个公共点A1,但点Q不与点A1重合,故不存在点Q使得Q∈平面PNBA1,故C错误;由选项A知P 平面MBN,故PQ 平面MBN,只需Q为A1D1的中点,则有PQ∥A1C1∥MN,所以PQ∥平面MBN,故D正确.故选AD.
9. SE=AE 如图,连接AC交BD于点O,连接OE.因为SC∥平面EBD,SC 平面SAC,平面SAC∩平面 EBD=OE,所以SC∥OE.又因为底面ABCD为平行四边形,O为对角线AC与BD的交点,故O为AC的中点,所以E为SA的中点,故当点E满足条件SE=AE 时,SC∥平面EBD.
10. AD,BC 显然AB,AC,DB,CD四条直线均与平面α相交.在△BCD中,由已知得EF∥BC,又EF α,BC α,所以BC∥α.同理,AD∥α,所以在题图中的6条直线中,与平面α平行的直线为AD,BC.
11. ①③ 对于①,由题意,得AB∥CF,AB=CF,所以四边形ABCF是平行四边形,所以AF∥BC.因为AF 平面BCD,BC 平面BCD,所以AF∥平面BCD,故①正确;对于②,如图,取DF的中点G,连接EG,CG.因为E是AD的中点,AF∥BC,AF=BC,所以EG=BC,EG∥BC,所以四边形BCGE为梯形,所以直线BE与直线CG相交,所以BE与平面CDF相交,故②错误;对于③,如图,连接AC,交BF于点O,连接OE.因为四边形ABCF是平行四边形,所以O是AC的中点,所以OE∥CD.因为OE 平面BEF,CD 平面BEF,所以CD∥平面BEF,故③正确.故正确结论的序号为①③.
12. 作EF∥DC交PD于点F,连接AF.
因为点E在棱PC上,且PE=2EC,所以FE=DC=2.
因为AB∥DC,AB=2,所以AB∥FE,且AB=FE,
所以四边形ABEF为平行四边形,则AF∥BE.
因为BE 平面PAD,AF 平面PAD,
所以BE∥平面PAD.
13. (1) 如图1,延长CQ和DA交于点E,连接PE,交AA1于点R,
即平面PQC与直线AA1交于点R.
因为Q为AB的中点,AQ∥DC,所以A为ED的中点,
所以AR=PD=DD1=AA1,所以=.
(2) 存在,当M为线段CC1上靠近点C的四等分点时,BM∥平面PQC,证明如下:
如图2,取PC的中点N,DC的中点G,连接NG,NM,则MN∥GC,且MN=GC,所以MN∥BQ,且MN=BQ,
所以四边形MNQB为平行四边形,
所以BM∥NQ.
又因为BM 平面PQC,NQ 平面PQC,
所以BM∥平面PQC.
图1 图2
13.2.3 直线与平面的位置关系
——直线与平面平行(2)
1. D 对于A,若直线l平行于平面α内的无数条直线,当这无数条直线是平行线时,l可能在平面内,与α不一定平行,故A不正确;对于B,若直线a在平面α外,则a∥α或a与α相交,故B不正确;对于C,若直线a∥b,b α,则a∥α或a α,故C不正确;对于D,若直线a∥b,b α,则a∥α或a α,所以a平行于平面α内的无数条直线,故D正确.
2. B 因为AB∥平面α,AB 平面ABDC,平面ABDC∩平面α=MN,所以AB∥MN. 又M是AC的中点,所以MN是梯形ABDC的中位线,故MN=(AB+CD)=5.
3. C 因为多面体A1B1C1-ABC是三棱台,所以AB∥A1B1.又AB 平面A1B1C1,A1B1 平面A1B1C1,所以AB∥平面A1B1C1,当AB 平面α,平面α∩平面A1B1C1=m时,由直线与平面平行的性质定理可知m∥AB,故选项C符合要求.
4. C 如图,连接MB交AC于点D,连接DN,NA,NC,MC,则平面NAC即为平面α.因为SB∥α,SB 平面SMB,平面SMB∩α=DN,所以SB∥DN.因为AB为底面圆的直径,点M,C将弧AB三等分,所以∠ABM=∠BMC=∠MBC=∠BAC=30°,MC=BC=AB,所以MC∥AB且MC=AB,所以==.又SB∥DN,所以==,所以=.
5. D 如图,连接AB1交A1B于点O,过点O作OP∥AC1交B1C1于点P,连接A1P,BP. 因为OP 平面A1PB,AC1 平面A1PB,所以AC1∥平面A1PB,即此时点P满足题意. 在△AB1C1中,==.又B1C1=2,所以PC1=1.
6. A 根据题意,不妨设该平面截空间四边形ABCD的四边得到四个交点E,F,G,H,AC∥平面EFGH,BD不平行于平面EFGH.因为AC∥平面EFGH,AC 平面ABC,且平面ABC∩平面EFGH=EF,所以AC∥EF,同理可得AC∥GH,所以GH∥EF.下面证明EH与FG不平行,假设EH∥FG,由FG 平面BCD,EH 平面BCD,得EH∥平面BCD.又因为EH 平面ABD,且平面ABD∩平面BCD=BD,由线面平行的性质定理可得EH∥BD.又EH 平面EFGH,BD 平面EFGH,所以BD∥平面EFGH,与题设BD不平行于平面EFGH矛盾,所以EH与FG不平行,所以四边形EFGH是梯形.
7. BC 过直线a可作无数个平面与α相交,由线面平行的性质定理可知,这些交线都与a平行,所以在平面α内与直线a平行的直线有无数条,故A不正确,B正确;若直线a平行于平面α,则直线a与平面α内的直线有两种位置关系:平行或异面,所以平面α内存在与a不平行的直线,且有无数条,故C正确,D不正确.故选BC.
8. AB 对于A,如图1,设A为MS的中点,底面为平行四边形STFE,连接PA,TA,则PA∥SE,PA=SE.又TQ∥SE,TQ=SE,所以PA∥TQ,PA=TQ,即四边形PATQ为平行四边形,所以PQ∥AT.又AT 平面MTS,PQ 平面MTS,所以PQ∥平面MST,故A正确;对于B,如图2,设A为MS的中点,底面为平行四边形STFE,连接PA,AT,则AP∥ES,AP=ES.又QT∥ES,QT=ES,故AP∥QT,AP=QT,即四边形APQT为平行四边形,所以PQ∥AT.又AT 平面MST,PQ 平面MST,所以PQ∥平面MST,故B正确;对于C,如图3,设A为ME的中点,底面为平行四边形GFES,连接QA,AS,设AQ交MT于点H,连接SH,则AQ∥FE,AQ=FE.又PS∥EF,PS=EF,所以AQ∥PS,AQ=PS,所以四边形AQPS为平行四边形,所以AS∥PQ.又PQ 平面AQPS,PQ 平面MST,平面AQPS∩平面MST=SH,假设PQ∥平面MST,则PQ∥SH,即在平面AQPS内过点S有两条直线和PQ都平行,这是不可能的,故C错误;对于D,如图4,设底面为平行四边形MQEF,连接ME,FQ交于点H,连接FQ,MT交于点G,则H为FQ的中点,连接SH,SG.因为S为PF的中点,所以SH∥PQ.又PQ 平面PFQ,PQ 平面MST,平面PFQ∩平面MST=SG,假设PQ∥平面MST,则PQ∥SG,即在平面PFQ内过点S有两条直线和PQ都平行,这是不可能的,故D错误.故选AB.
图1 图2 图3 图4
9. 1 因为A1B∥平面B1CD,A1B 平面A1BC1,平面A1BC1∩平面B1CD=OD,所以A1B∥OD.因为四边形BCC1B1是菱形,所以O为BC1的中点,所以D为A1C1的中点,即=1.
10. 因为A1C1∥AC,MN∥A1C1,所以MN∥AC. 由线面平行的判定定理和性质定理可知MN∥PQ,所以PQ∥AC,所以=,即=,即PQ=.
11. 因为EF∥平面AB1C,EF 平面ABCD,且平面ABCD∩平面AB1C=AC,所以EF∥AC.又E是AD的中点,所以F是CD的中点.因为在Rt△DEF中,DE=DF=1,所以EF=.
12. (1) 如图,取PD的中点E,连接AE,NE.
因为N,E分别为PC,PD的中点,
所以NE∥DC,且NE=DC.
又M为AB的中点,AB∥DC,AB=DC,
所以AM∥NE,且AM=NE,
所以四边形AMNE为平行四边形,
所以AE∥MN.
又AE 平面PAD,MN 平面PAD,
所以MN∥平面PAD.
(2) 因为四边形ABCD为平行四边形,
所以AD∥BC.
又BC 平面PAD,AD 平面PAD,
所以BC∥平面PAD.
又平面PAD∩平面PBC=l,BC 平面PBC,
所以BC∥l.
13. (1) 如图,连接AC交BD于点O,连接OG.
因为四边形ABCD为直角梯形,DC=2AB,
所以AB∥CD,所以==.
又因为GC=2FG,==,所以AF∥OG.
因为OG 平面BDG,AF 平面BDG,
所以AF∥平面BDG.
(2) 因为四边形ABCD为直角梯形,DC=2AB,
所以AB∥CD.
因为CD 平面CDEF,AB 平面CDEF,
所以AB∥平面CDEF.
因为AB 平面ABFE,平面CDEF∩平面ABFE=EF,
所以AB∥EF.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
