14.4.1 用样本估计总体的集中趋势参数 练习(含详解)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 14.4.1 用样本估计总体的集中趋势参数 练习(含详解)2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 147.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 00:00:00 | ||
图片预览

文档简介
14.4.1 用样本估计总体的集中趋势参数
一、 单项选择题
1 (2024河南月考)样本数据12,11,7,15,9,10,12,8的中位数是( )
A. 12 B. 11 C. 10 D. 10.5
2 (2024葫芦岛一模)从某班所有同学中随机抽取10人,获得他们某学年参加社区服务次数的数据如下:4,4,4,7,7,8,8,9,9,10,则这组数据的众数是( )
A. 9 B. 8 C. 7 D. 4
3 (2024河北月考)用简单随机抽样的方法抽取某小区20户家庭的日均用电量(单位:kW·h),统计的数据如下:
日均用电量/kW·h 4 5 6 7 8 10
户数 1 2 4 6 5 2
根据样本数据,估计该小区200户家庭日均用电量的平均数( )
A. 一定为7 kW·h B. 一定高于8 kW·h
C. 一定低于7 kW·h D. 约为7 kW·h
4 (2024江西联考)某中学举办了一次知识竞赛,从中随机抽取了部分学生的成绩绘制出如图所示的频率直方图,则估计该中学的学生本次竞赛成绩的中位数为( )
A. 68 B. 71 C. 75 D. 79
5 (2023福建月考)某市昼夜温差大,是内陆地区发展特色农业的天然宝地,干热河谷所孕育的早春蔬菜为大家送去新鲜优质的维生素和膳食纤维.下图为该市2023年3月6日至12日的最高气温与最低气温的天气预报数据,则下列说法中错误的是( )
A. 这7天的单日最大温差为17 ℃的有2天
B. 这7天的最高气温的中位数为29 ℃
C. 这7天的最高气温的众数为29 ℃
D. 这7天的最高气温的平均数为29 ℃
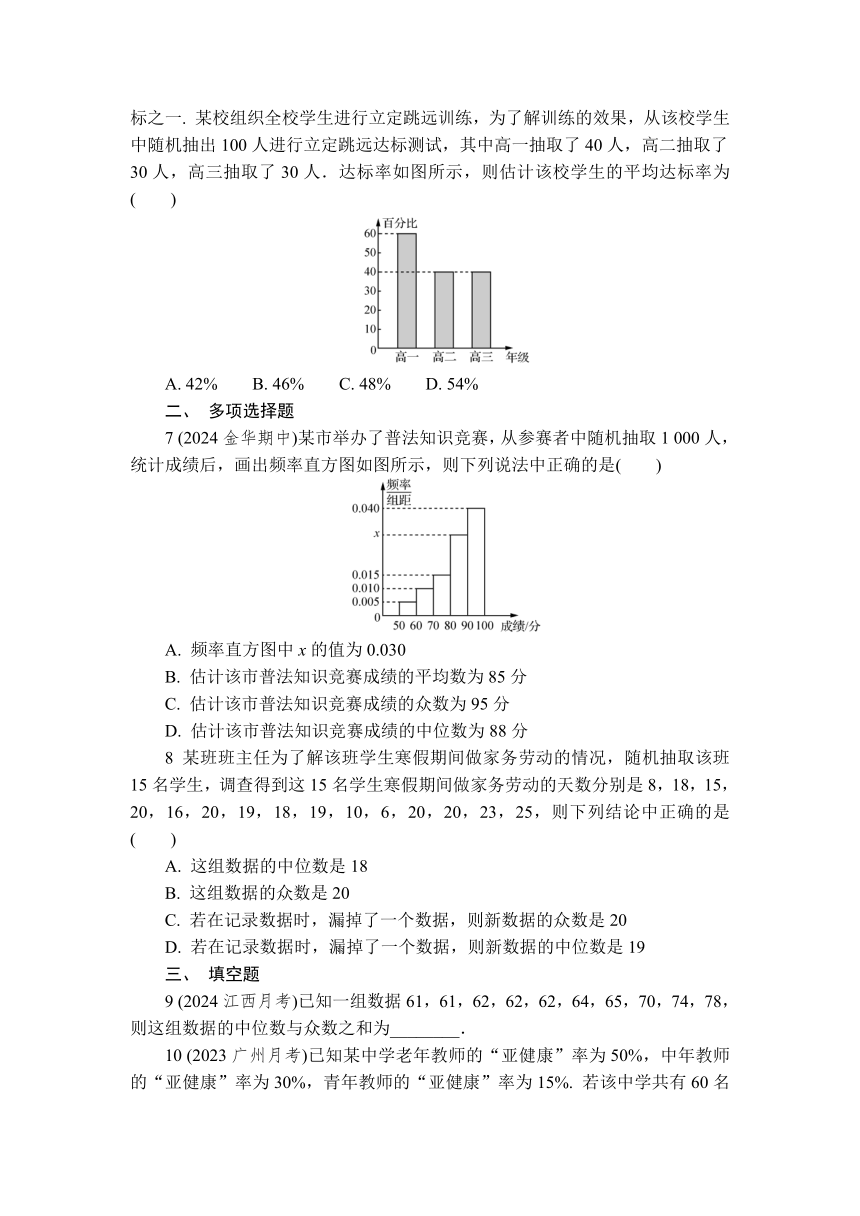
6 (2023榆林模拟)大力开展体育活动,增强学生体质,是学校教育的重要目标之一. 某校组织全校学生进行立定跳远训练,为了解训练的效果,从该校学生中随机抽出100人进行立定跳远达标测试,其中高一抽取了40人,高二抽取了30人,高三抽取了30人.达标率如图所示,则估计该校学生的平均达标率为( )
A. 42% B. 46% C. 48% D. 54%
二、 多项选择题
7 (2024金华期中)某市举办了普法知识竞赛,从参赛者中随机抽取1 000人,统计成绩后,画出频率直方图如图所示,则下列说法中正确的是( )
A. 频率直方图中x的值为0.030
B. 估计该市普法知识竞赛成绩的平均数为85分
C. 估计该市普法知识竞赛成绩的众数为95分
D. 估计该市普法知识竞赛成绩的中位数为88分
8 某班班主任为了解该班学生寒假期间做家务劳动的情况,随机抽取该班15名学生,调查得到这15名学生寒假期间做家务劳动的天数分别是8,18,15,20,16,20,19,18,19,10,6,20,20,23,25,则下列结论中正确的是( )
A. 这组数据的中位数是18
B. 这组数据的众数是20
C. 若在记录数据时,漏掉了一个数据,则新数据的众数是20
D. 若在记录数据时,漏掉了一个数据,则新数据的中位数是19
三、 填空题
9 (2024江西月考)已知一组数据61,61,62,62,62,64,65,70,74,78,则这组数据的中位数与众数之和为________.
10 (2023广州月考)已知某中学老年教师的“亚健康”率为50%,中年教师的“亚健康”率为30%,青年教师的“亚健康”率为15%. 若该中学共有60名老年教师,100名中年教师,200名青年教师,则该校教师的“亚健康”率为________.
11 已知有四个数2,3,a,b,这四个数的中位数为5,平均数为6,则ab=________.
四、 解答题
12 (2023福建月考)高一(3)班有男同学27人、女同学21人,在一次语文测验中,男同学成绩的平均数是82分,中位数是75分,女同学成绩的平均数是80分,中位数是80分.
(1) 求这次测验全班的平均分(精确到0.01);
(2) 估计全班成绩在80分以下(含80分)的同学至少有多少人?
(3) 分析男同学成绩的平均数与中位数相差较大的主要原因是什么?
13 (2024云南月考)近年来,由于互联网的普及,直播带货已经成为推动消费的一种营销形式.某直播平台工作人员在问询了本平台600个直播商家的利润状况后,随机抽取了100个商家的平均日利润(单位:百元)进行了统计,所得的频率直方图如图所示.
(1) 求m的值,并估计该直播平台商家平均日利润的中位数与平均数(同一组中的数据用该组区间的中点值作代表);
(2) 以样本估计总体,该直播平台为了鼓励直播带货,提出了两种奖励方案,一是对平均日利润超过78百元的商家进行奖励;二是对平均日利润排名在前的商家进行奖励.若两种奖励方案只选择一种,那么你觉得哪种方案受到奖励的商家更多?并说明理由.
14.4.1 用样本估计总体的集中趋势参数
1. D 将数据从小到大排列为7,8,9,10,11,12,12,15.故这组数据的中位数是=10.5.
2. D 由数据可知服务次数为4的人数最多,故众数为4.
3. D 因为抽取的20户家庭的日均用电量的平均数为(4×1+5×2+6×4+7×6+8×5+10×2)=7(kW·h),所以可以估计该小区200户家庭的日均用电量的平均数约为7 kW·h.
4. B 设m为该中学的学生本次竞赛成绩的中位数,因为(0.016+0.030)×10=0.46<0.5,(0.016+0.030+0.040)×10=0.86>0.5,所以m在区间[70,80)上,所以(m-70)×0.04+0.46=0.5,解得m=71.
5. D 对于A,这7天的单日最大温差为17 ℃的有3月10日,3月12日,共2天,故A正确;对于B,这7天的最高气温从小到大依次为28,28,29,29,29,30,31(单位:℃),故这7天的最高气温的中位数为29 ℃,故B正确;对于C,这7天的最高气温的众数为29 ℃,故C正确;对于D,这7天的最高气温的平均数为(28×2+29×3+30+31)=>29,故D错误.
6. C 估计该校学生的平均达标率为(40×60%+30×40%+30×40%)×100%=48%.
7. AC 对于A,由图可知10×(0.005+0.010+0.015+x+0.040)=1,解得x=0.030,故A正确;对于B,由图可知该市普法知识竞赛成绩的平均数为55×0.05+65×0.1+75×0.15+85×0.3+95×0.4=84(分),故B错误;对于C,由图可知该市普法知识竞赛成绩的众数为95分,故C正确;对于D,因为前3组的频率和为0.05+0.1+0.15=0.3<0.5,前4组的频率和为0.3+0.3=0.6>0.5,所以中位数在80到90之间,设中位数为m,则0.3+0.03(m-80)=0.5,解得m≈87,故D错误.故选AC.
8. BC 将这组数据按从小到大的顺序排列6,8,10,15,16,18,18,19,19,20,20,20,20,23,25.根据中位数和众数的定义,可得数据的中位数和众数分别是19和20,故A错误,B正确;若漏掉了一个数据,新数据中出现最多的数仍然是20,故C正确;若漏掉的数据为19,则新数据的中位数是18.5,故D错误.故选BC.
9. 125 由中位数和众数的定义可知中位数a==63,众数b=62,所以a+b=125.
10. 25% 由题意,得该校教师的“亚健康”率为=25%.
11. 84 因为2,3,a,b的中位数为5,平均数为6,所以 a>6,b>6.当a≤b时,=5,=6,解得a=7,b=12,ab=84;当a>b时,=5,=6,解得a=12,b=7,ab=84.综上,ab=84.
12. (1) 因为27名男同学的平均分是82分,21名女同学的平均分是80分,所以这次语文测验全班成绩的平均分为=≈81.13(分).
(2) 因为男同学成绩的中位数是75分,
所以至少有14人得分不超过75分.
因为女同学成绩的中位数是80分,
所以至少有11人得分不超过80分,
所以全班至少有25人的成绩在80分及80分以下.
(3) 男同学成绩的平均数与中位数的相差较大,说明男同学的成绩两极分化现象严重,得分高的成绩和得分低的成绩相差较大.
13. (1) 由题意可知(0.005×2+0.015+m+0.025+0.03)×10=1,解得m=0.02.
设中位数为n,则0.05+0.15+0.2+(n-70)×0.025=0.5,解得n=74,所以中位数为74.
平均数为(45+95)×0.05+55×0.15+65×0.2+75×0.25+85×0.3=72.5.
(2) 由题意可知方案一受到奖励的商家的个数为(×0.25+0.3+0.05)×600=240,
方案二受到奖励的商家的个数为×600=200,
因为240>200,所以方案一受到奖励的商家更多.
一、 单项选择题
1 (2024河南月考)样本数据12,11,7,15,9,10,12,8的中位数是( )
A. 12 B. 11 C. 10 D. 10.5
2 (2024葫芦岛一模)从某班所有同学中随机抽取10人,获得他们某学年参加社区服务次数的数据如下:4,4,4,7,7,8,8,9,9,10,则这组数据的众数是( )
A. 9 B. 8 C. 7 D. 4
3 (2024河北月考)用简单随机抽样的方法抽取某小区20户家庭的日均用电量(单位:kW·h),统计的数据如下:
日均用电量/kW·h 4 5 6 7 8 10
户数 1 2 4 6 5 2
根据样本数据,估计该小区200户家庭日均用电量的平均数( )
A. 一定为7 kW·h B. 一定高于8 kW·h
C. 一定低于7 kW·h D. 约为7 kW·h
4 (2024江西联考)某中学举办了一次知识竞赛,从中随机抽取了部分学生的成绩绘制出如图所示的频率直方图,则估计该中学的学生本次竞赛成绩的中位数为( )
A. 68 B. 71 C. 75 D. 79
5 (2023福建月考)某市昼夜温差大,是内陆地区发展特色农业的天然宝地,干热河谷所孕育的早春蔬菜为大家送去新鲜优质的维生素和膳食纤维.下图为该市2023年3月6日至12日的最高气温与最低气温的天气预报数据,则下列说法中错误的是( )
A. 这7天的单日最大温差为17 ℃的有2天
B. 这7天的最高气温的中位数为29 ℃
C. 这7天的最高气温的众数为29 ℃
D. 这7天的最高气温的平均数为29 ℃
6 (2023榆林模拟)大力开展体育活动,增强学生体质,是学校教育的重要目标之一. 某校组织全校学生进行立定跳远训练,为了解训练的效果,从该校学生中随机抽出100人进行立定跳远达标测试,其中高一抽取了40人,高二抽取了30人,高三抽取了30人.达标率如图所示,则估计该校学生的平均达标率为( )
A. 42% B. 46% C. 48% D. 54%
二、 多项选择题
7 (2024金华期中)某市举办了普法知识竞赛,从参赛者中随机抽取1 000人,统计成绩后,画出频率直方图如图所示,则下列说法中正确的是( )
A. 频率直方图中x的值为0.030
B. 估计该市普法知识竞赛成绩的平均数为85分
C. 估计该市普法知识竞赛成绩的众数为95分
D. 估计该市普法知识竞赛成绩的中位数为88分
8 某班班主任为了解该班学生寒假期间做家务劳动的情况,随机抽取该班15名学生,调查得到这15名学生寒假期间做家务劳动的天数分别是8,18,15,20,16,20,19,18,19,10,6,20,20,23,25,则下列结论中正确的是( )
A. 这组数据的中位数是18
B. 这组数据的众数是20
C. 若在记录数据时,漏掉了一个数据,则新数据的众数是20
D. 若在记录数据时,漏掉了一个数据,则新数据的中位数是19
三、 填空题
9 (2024江西月考)已知一组数据61,61,62,62,62,64,65,70,74,78,则这组数据的中位数与众数之和为________.
10 (2023广州月考)已知某中学老年教师的“亚健康”率为50%,中年教师的“亚健康”率为30%,青年教师的“亚健康”率为15%. 若该中学共有60名老年教师,100名中年教师,200名青年教师,则该校教师的“亚健康”率为________.
11 已知有四个数2,3,a,b,这四个数的中位数为5,平均数为6,则ab=________.
四、 解答题
12 (2023福建月考)高一(3)班有男同学27人、女同学21人,在一次语文测验中,男同学成绩的平均数是82分,中位数是75分,女同学成绩的平均数是80分,中位数是80分.
(1) 求这次测验全班的平均分(精确到0.01);
(2) 估计全班成绩在80分以下(含80分)的同学至少有多少人?
(3) 分析男同学成绩的平均数与中位数相差较大的主要原因是什么?
13 (2024云南月考)近年来,由于互联网的普及,直播带货已经成为推动消费的一种营销形式.某直播平台工作人员在问询了本平台600个直播商家的利润状况后,随机抽取了100个商家的平均日利润(单位:百元)进行了统计,所得的频率直方图如图所示.
(1) 求m的值,并估计该直播平台商家平均日利润的中位数与平均数(同一组中的数据用该组区间的中点值作代表);
(2) 以样本估计总体,该直播平台为了鼓励直播带货,提出了两种奖励方案,一是对平均日利润超过78百元的商家进行奖励;二是对平均日利润排名在前的商家进行奖励.若两种奖励方案只选择一种,那么你觉得哪种方案受到奖励的商家更多?并说明理由.
14.4.1 用样本估计总体的集中趋势参数
1. D 将数据从小到大排列为7,8,9,10,11,12,12,15.故这组数据的中位数是=10.5.
2. D 由数据可知服务次数为4的人数最多,故众数为4.
3. D 因为抽取的20户家庭的日均用电量的平均数为(4×1+5×2+6×4+7×6+8×5+10×2)=7(kW·h),所以可以估计该小区200户家庭的日均用电量的平均数约为7 kW·h.
4. B 设m为该中学的学生本次竞赛成绩的中位数,因为(0.016+0.030)×10=0.46<0.5,(0.016+0.030+0.040)×10=0.86>0.5,所以m在区间[70,80)上,所以(m-70)×0.04+0.46=0.5,解得m=71.
5. D 对于A,这7天的单日最大温差为17 ℃的有3月10日,3月12日,共2天,故A正确;对于B,这7天的最高气温从小到大依次为28,28,29,29,29,30,31(单位:℃),故这7天的最高气温的中位数为29 ℃,故B正确;对于C,这7天的最高气温的众数为29 ℃,故C正确;对于D,这7天的最高气温的平均数为(28×2+29×3+30+31)=>29,故D错误.
6. C 估计该校学生的平均达标率为(40×60%+30×40%+30×40%)×100%=48%.
7. AC 对于A,由图可知10×(0.005+0.010+0.015+x+0.040)=1,解得x=0.030,故A正确;对于B,由图可知该市普法知识竞赛成绩的平均数为55×0.05+65×0.1+75×0.15+85×0.3+95×0.4=84(分),故B错误;对于C,由图可知该市普法知识竞赛成绩的众数为95分,故C正确;对于D,因为前3组的频率和为0.05+0.1+0.15=0.3<0.5,前4组的频率和为0.3+0.3=0.6>0.5,所以中位数在80到90之间,设中位数为m,则0.3+0.03(m-80)=0.5,解得m≈87,故D错误.故选AC.
8. BC 将这组数据按从小到大的顺序排列6,8,10,15,16,18,18,19,19,20,20,20,20,23,25.根据中位数和众数的定义,可得数据的中位数和众数分别是19和20,故A错误,B正确;若漏掉了一个数据,新数据中出现最多的数仍然是20,故C正确;若漏掉的数据为19,则新数据的中位数是18.5,故D错误.故选BC.
9. 125 由中位数和众数的定义可知中位数a==63,众数b=62,所以a+b=125.
10. 25% 由题意,得该校教师的“亚健康”率为=25%.
11. 84 因为2,3,a,b的中位数为5,平均数为6,所以 a>6,b>6.当a≤b时,=5,=6,解得a=7,b=12,ab=84;当a>b时,=5,=6,解得a=12,b=7,ab=84.综上,ab=84.
12. (1) 因为27名男同学的平均分是82分,21名女同学的平均分是80分,所以这次语文测验全班成绩的平均分为=≈81.13(分).
(2) 因为男同学成绩的中位数是75分,
所以至少有14人得分不超过75分.
因为女同学成绩的中位数是80分,
所以至少有11人得分不超过80分,
所以全班至少有25人的成绩在80分及80分以下.
(3) 男同学成绩的平均数与中位数的相差较大,说明男同学的成绩两极分化现象严重,得分高的成绩和得分低的成绩相差较大.
13. (1) 由题意可知(0.005×2+0.015+m+0.025+0.03)×10=1,解得m=0.02.
设中位数为n,则0.05+0.15+0.2+(n-70)×0.025=0.5,解得n=74,所以中位数为74.
平均数为(45+95)×0.05+55×0.15+65×0.2+75×0.25+85×0.3=72.5.
(2) 由题意可知方案一受到奖励的商家的个数为(×0.25+0.3+0.05)×600=240,
方案二受到奖励的商家的个数为×600=200,
因为240>200,所以方案一受到奖励的商家更多.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
