第四章专题复习:全等三角形的常见模型 课件(共28张PPT)
文档属性
| 名称 | 第四章专题复习:全等三角形的常见模型 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 955.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 00:00:00 | ||
图片预览

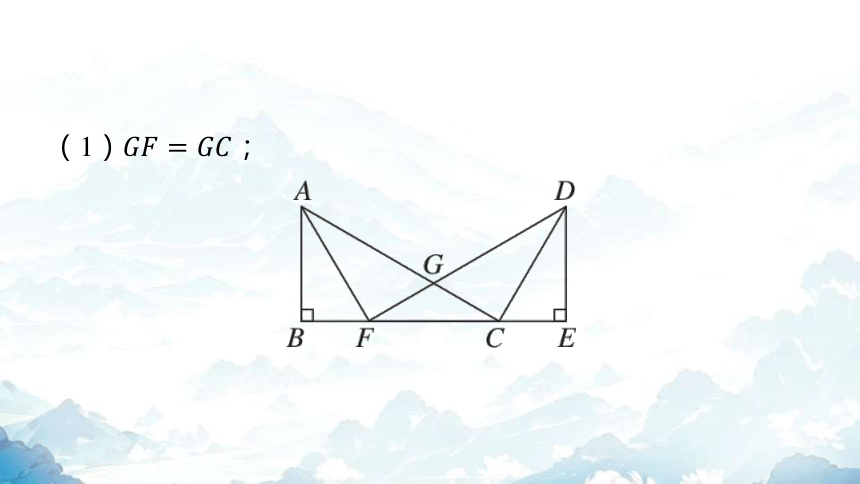


文档简介
(共28张PPT)
2025新七年级数学下册
第四章
——全等三角形的常见模型专题复习
类型1 平移模型
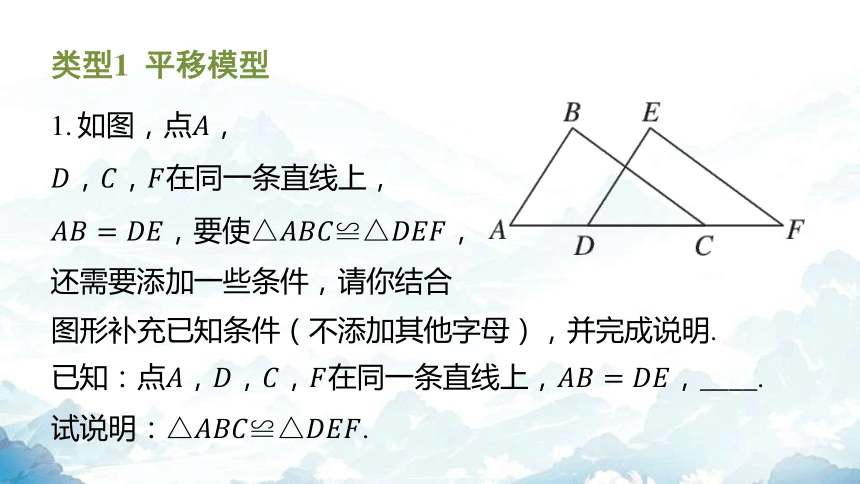
1. 如图,点 ,
,, 在同一条直线上,
,要使 ,
还需要添加一些条件,请你结合
已知:点,,,在同一条直线上, ,____.
试说明: .
图形补充已知条件(不添加其他字母),并完成说明.
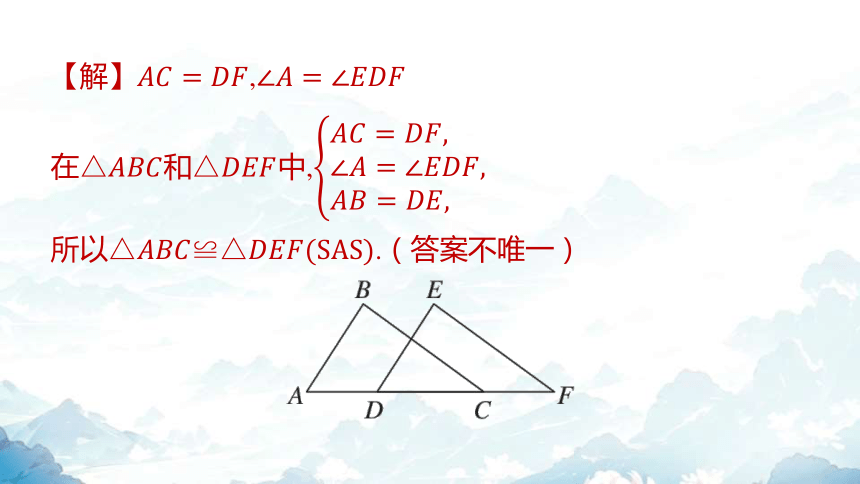
【解】,
在和中,
所以 .(答案不唯一)
类型2 对称模型
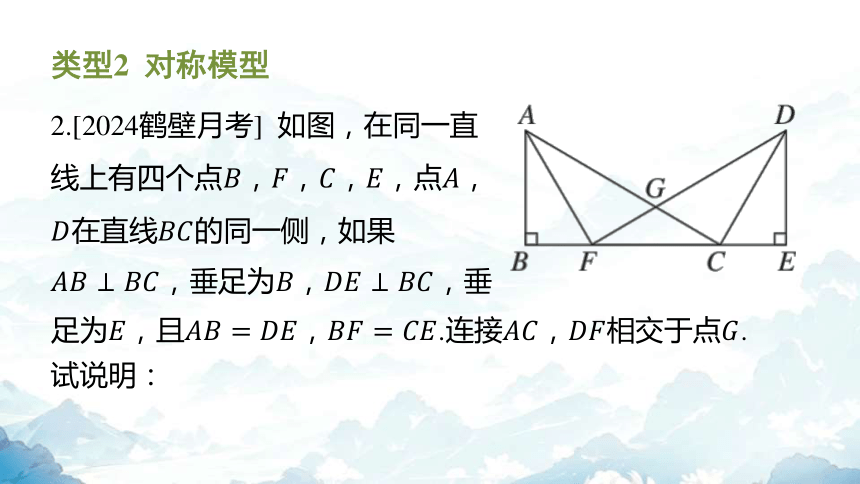
2.[2024鹤壁月考] 如图,在同一直
线上有四个点,,,,点 ,
在直线 的同一侧,如果
,垂足为, ,垂
试说明:
足为,且,.连接,相交于点 .
(1) ;
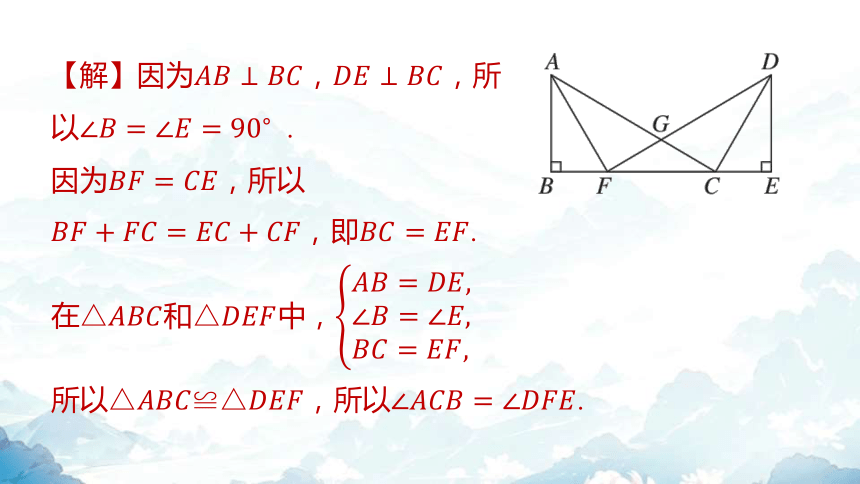
【解】因为, ,所
以 .
因为 ,所以
,即 .
在和中,
所以,所以 .
作的平分线交于点 ,则
.
又因为 ,所以
.
所以 .
(2) .
【解】由(1)知,所以 .
又因为 ,
所以,即 .
在和中,
所以 .
类型3 旋转模型
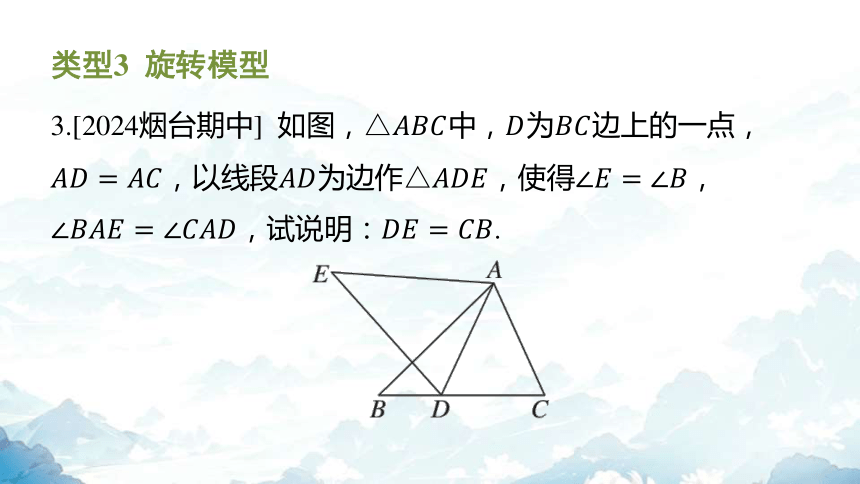
3.[2024烟台期中] 如图,中,为 边上的一点,
,以线段为边作,使得 ,
,试说明: .
【解】因为 ,
所以 ,
即 .
在和 中,
所以,所以 .
4.[2024梧州期中] 如图,和中, ,
, ,连接, .
(1)试说明: ;
【解】因为 ,
所以 .
在和中,
所以.所以 .
(2)延长交于点,试说明: .
【解】设交于点 .
因为 ,所以
.
又因为 ,
,
, ,
所以 ,所以 .
类型4 半角模型
5.如图,正方形中, ,它的
两边分别交边,于点, .
试说明: .
【解】如图,延长到,使,连接 .
因为四边形 是正方形,
所以 , .所以
.
在和 中,
所以.所以 ,
.
因为 ,所以 .
所以 ,即
.
在和中,
所以.所以 .
所以 .
6.如图,在中,, ,
,是斜边上两点,且 ,若 ,
,,求与 的面积之和.
【解】如图,作关于 的对称图
形,连接 ,
则, ,
,
所以 .
由题意得 ,
所以 .
在和中,
所以 .
所以, , .
所以 ,即 是直角三角形.
所以 .
所以,即与 的面积之和为21.
类型5 一线三等角模型
7.[2024重庆沙坪坝区期中] 已知,中, ,
,一直线过顶点,过, 分别作其垂线,垂
足分别为, .
(1)如图①,试说明: ;
【解】因为 ,所以
.
因为, ,所以
.
所以 .所以 .
在和 中,
所以 .所以
, .
又因为 ,所以
.
(2)如图②,,, 之间的数量关系为____________
___;
【解析】因为 ,
,所以 .
所以 .
又因为 ,
,所以
,
所以, .
所以 .
(3)在(2)的条件下,若,,求
的面积.
【解】由(2)得.因为 ,
所以.所以易知.所以 .
所以的面积 .
2025新七年级数学下册
第四章
——全等三角形的常见模型专题复习
类型1 平移模型
1. 如图,点 ,
,, 在同一条直线上,
,要使 ,
还需要添加一些条件,请你结合
已知:点,,,在同一条直线上, ,____.
试说明: .
图形补充已知条件(不添加其他字母),并完成说明.
【解】,
在和中,
所以 .(答案不唯一)
类型2 对称模型
2.[2024鹤壁月考] 如图,在同一直
线上有四个点,,,,点 ,
在直线 的同一侧,如果
,垂足为, ,垂
试说明:
足为,且,.连接,相交于点 .
(1) ;
【解】因为, ,所
以 .
因为 ,所以
,即 .
在和中,
所以,所以 .
作的平分线交于点 ,则
.
又因为 ,所以
.
所以 .
(2) .
【解】由(1)知,所以 .
又因为 ,
所以,即 .
在和中,
所以 .
类型3 旋转模型
3.[2024烟台期中] 如图,中,为 边上的一点,
,以线段为边作,使得 ,
,试说明: .
【解】因为 ,
所以 ,
即 .
在和 中,
所以,所以 .
4.[2024梧州期中] 如图,和中, ,
, ,连接, .
(1)试说明: ;
【解】因为 ,
所以 .
在和中,
所以.所以 .
(2)延长交于点,试说明: .
【解】设交于点 .
因为 ,所以
.
又因为 ,
,
, ,
所以 ,所以 .
类型4 半角模型
5.如图,正方形中, ,它的
两边分别交边,于点, .
试说明: .
【解】如图,延长到,使,连接 .
因为四边形 是正方形,
所以 , .所以
.
在和 中,
所以.所以 ,
.
因为 ,所以 .
所以 ,即
.
在和中,
所以.所以 .
所以 .
6.如图,在中,, ,
,是斜边上两点,且 ,若 ,
,,求与 的面积之和.
【解】如图,作关于 的对称图
形,连接 ,
则, ,
,
所以 .
由题意得 ,
所以 .
在和中,
所以 .
所以, , .
所以 ,即 是直角三角形.
所以 .
所以,即与 的面积之和为21.
类型5 一线三等角模型
7.[2024重庆沙坪坝区期中] 已知,中, ,
,一直线过顶点,过, 分别作其垂线,垂
足分别为, .
(1)如图①,试说明: ;
【解】因为 ,所以
.
因为, ,所以
.
所以 .所以 .
在和 中,
所以 .所以
, .
又因为 ,所以
.
(2)如图②,,, 之间的数量关系为____________
___;
【解析】因为 ,
,所以 .
所以 .
又因为 ,
,所以
,
所以, .
所以 .
(3)在(2)的条件下,若,,求
的面积.
【解】由(2)得.因为 ,
所以.所以易知.所以 .
所以的面积 .
同课章节目录
