第五章专题复习:等腰三角形的三线合一 课件(共21张PPT)
文档属性
| 名称 | 第五章专题复习:等腰三角形的三线合一 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 747.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 09:15:37 | ||
图片预览

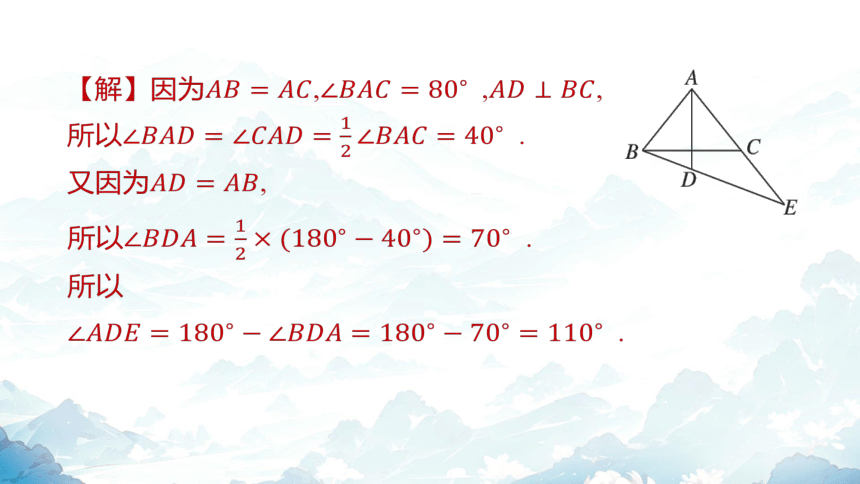


文档简介
(共21张PPT)
2025新七年级数学下册
第五章
——等腰三角形的三线合一专题复习
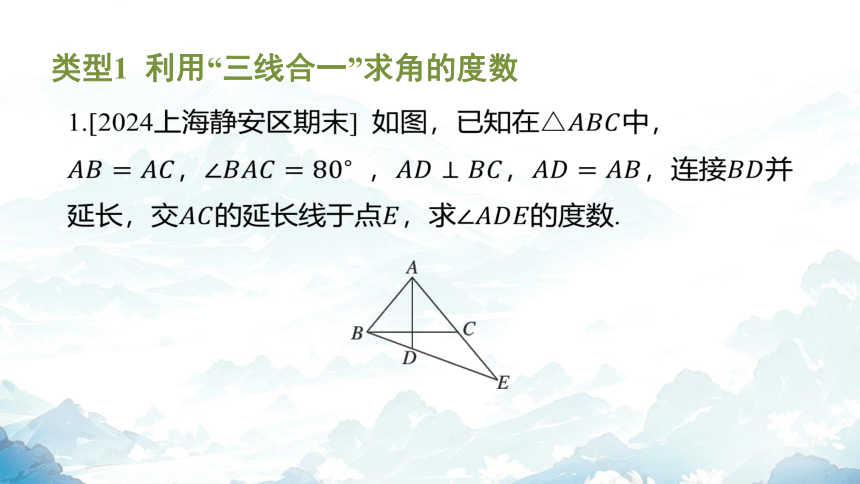
类型1 利用“三线合一”求角的度数
1.[2024上海静安区期末] 如图,已知在 中,
, ,,,连接 并
延长,交的延长线于点,求 的度数.
【解】因为, , ,
所以 .
又因为 ,
所以 .
所以
.
类型2 利用“三线合一”求线段的长
2.[2024遂宁期末] 如图,在 中,
,,于点 ,若
,且的周长为24,求 的长.
【解】因为的周长 ,
且 ,
所以 .
因为 ,
所以 .
又因为,所以.因为 ,
,
所以 .
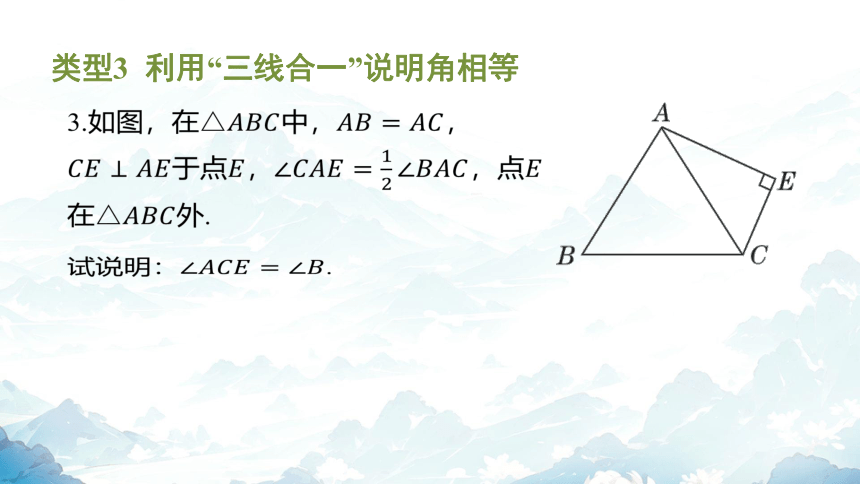
类型3 利用“三线合一”说明角相等
3.如图,在中, ,
于点,,点
在 外.
试说明: .
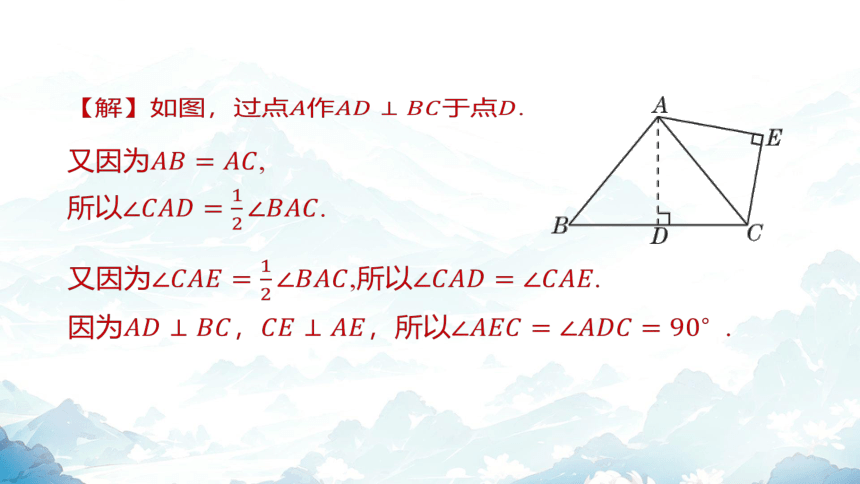
【解】如图,过点作于点 .
又因为 ,
所以 .
又因为,所以 .
因为,,所以 .
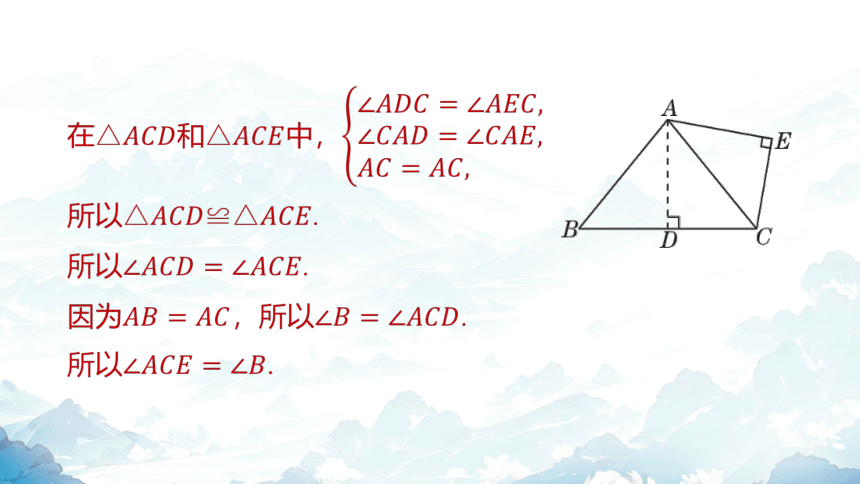
在和中,
所以 .
所以 .
因为,所以 .
所以 .
类型4 利用“三线合一”说明线段相等
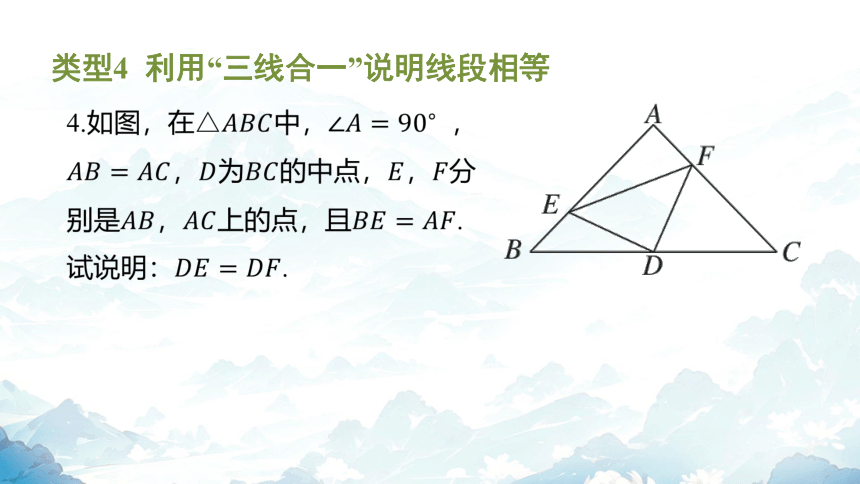
4.如图,在中, ,
,为的中点,, 分
别是,上的点,且 .
试说明: .
【解】如图,连接 .
因为,为 的中点,
,所以 ,
.
.
所以 .
所以易得 .
又因为 ,
所以 .
所以 .
类型5 利用“三线合一”说明角的倍分关系
5.如图,在中,,于点 .试说明:
.
【解】过点作于点 .则
.所以 .
因为,,所以平分 .
所以 .
因为,所以 .所以
.
所以 .
所以 .
类型6 利用“三线合一”说明线段的垂直关系
6.如图,在中,,平分,是 上
一点,且.试说明: .
【解】如图,过点作 于点
,
所以 .
又因为,所以 .
又因为,所以 .
因为平分,所以 .
又因为,所以 .
所以 ,
即 .
类型7 利用“三线合一”说明线段的倍分关系(构造三线法)
7.[2024无锡模拟] 如图,已知在等腰直角三角形 中,
, ,平分,交 的
延长线于点.试说明: .
【解】如图,延长,交于点 .
因为平分, ,
所以, .
又因为 ,
所以 .
所以.所以 .
因为 , , ,
所以 .
又因为, ,
所以 .
所以.所以 .
类型8 利用“三线合一”说明线段的和差关系(构造三线法)
8.如图,在中,于点,且 .试说
明: .
【解】如图,以点为圆心, 长为半径
画弧交于点,连接 ,
则,所以 .
又因为 ,
所以是的边 上的中线.
所以 .
又因为 ,
所以 .
因为 ,
所以.所以易得 .
所以 .
所以 .
2025新七年级数学下册
第五章
——等腰三角形的三线合一专题复习
类型1 利用“三线合一”求角的度数
1.[2024上海静安区期末] 如图,已知在 中,
, ,,,连接 并
延长,交的延长线于点,求 的度数.
【解】因为, , ,
所以 .
又因为 ,
所以 .
所以
.
类型2 利用“三线合一”求线段的长
2.[2024遂宁期末] 如图,在 中,
,,于点 ,若
,且的周长为24,求 的长.
【解】因为的周长 ,
且 ,
所以 .
因为 ,
所以 .
又因为,所以.因为 ,
,
所以 .
类型3 利用“三线合一”说明角相等
3.如图,在中, ,
于点,,点
在 外.
试说明: .
【解】如图,过点作于点 .
又因为 ,
所以 .
又因为,所以 .
因为,,所以 .
在和中,
所以 .
所以 .
因为,所以 .
所以 .
类型4 利用“三线合一”说明线段相等
4.如图,在中, ,
,为的中点,, 分
别是,上的点,且 .
试说明: .
【解】如图,连接 .
因为,为 的中点,
,所以 ,
.
.
所以 .
所以易得 .
又因为 ,
所以 .
所以 .
类型5 利用“三线合一”说明角的倍分关系
5.如图,在中,,于点 .试说明:
.
【解】过点作于点 .则
.所以 .
因为,,所以平分 .
所以 .
因为,所以 .所以
.
所以 .
所以 .
类型6 利用“三线合一”说明线段的垂直关系
6.如图,在中,,平分,是 上
一点,且.试说明: .
【解】如图,过点作 于点
,
所以 .
又因为,所以 .
又因为,所以 .
因为平分,所以 .
又因为,所以 .
所以 ,
即 .
类型7 利用“三线合一”说明线段的倍分关系(构造三线法)
7.[2024无锡模拟] 如图,已知在等腰直角三角形 中,
, ,平分,交 的
延长线于点.试说明: .
【解】如图,延长,交于点 .
因为平分, ,
所以, .
又因为 ,
所以 .
所以.所以 .
因为 , , ,
所以 .
又因为, ,
所以 .
所以.所以 .
类型8 利用“三线合一”说明线段的和差关系(构造三线法)
8.如图,在中,于点,且 .试说
明: .
【解】如图,以点为圆心, 长为半径
画弧交于点,连接 ,
则,所以 .
又因为 ,
所以是的边 上的中线.
所以 .
又因为 ,
所以 .
因为 ,
所以.所以易得 .
所以 .
所以 .
同课章节目录
