北师大版九年级数学下3.2圆的对称性课件(共22张PPT)
文档属性
| 名称 | 北师大版九年级数学下3.2圆的对称性课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-11 22:03:02 | ||
图片预览



文档简介
课件22张PPT。遇到困难不要抱怨,既然改
变不了过去,那就改变未来。金塔县第四中学 马晓艳九年级数学(下)第三章: 圆第二节 圆的对称性
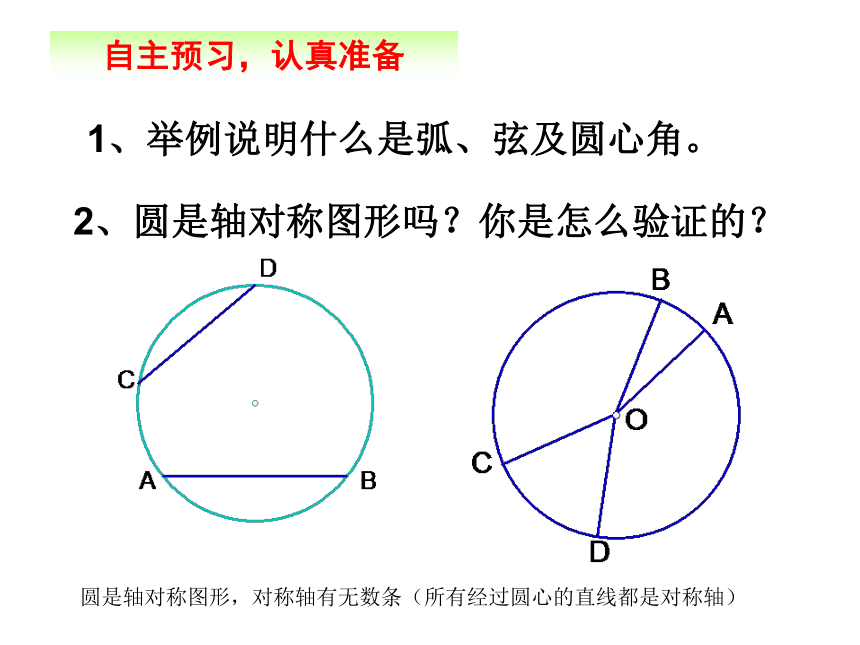
1、举例说明什么是弧、弦及圆心角。
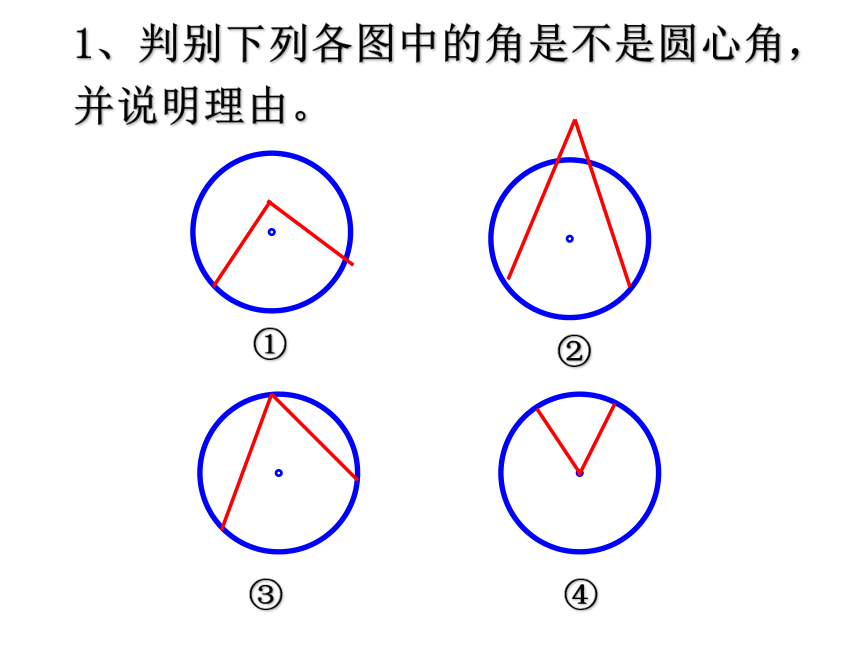
2、圆是轴对称图形吗?你是怎么验证的?自主预习,认真准备圆是轴对称图形,对称轴有无数条(所有经过圆心的直线都是对称轴)1、判别下列各图中的角是不是圆心角,
并说明理由。①②③④ 请同学们观察屏幕上两个半径相等的圆。请回答: 它们能重合吗?如果能重合,请将它们的圆心
固定在一起。 然后将其中一个圆旋转任意一个角度,这时两个
圆还重合吗 ?圆具有旋转不变性,即一个圆绕着它的圆心
旋转任意一个角度,都能与原来的圆重合。
即因此,圆是中心对称圆形,对称中心为圆
心。圆的中心对称性是其旋转不变性的特例.自主探究 合作交流任务一:探究圆的旋转不变性按下面的步骤做一做
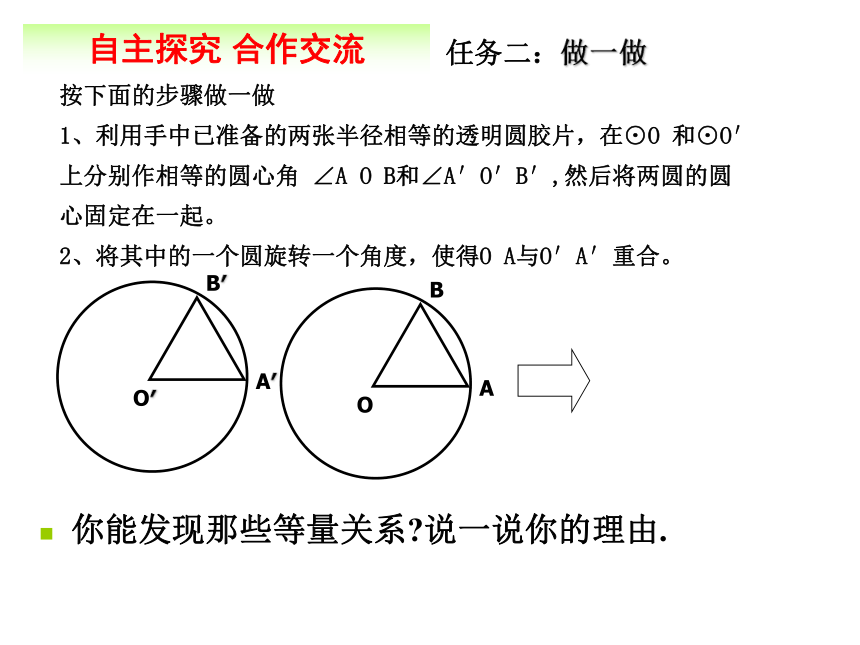
1、利用手中已准备的两张半径相等的透明圆胶片,在⊙O 和⊙O′
上分别作相等的圆心角 ∠A O B和∠A′O′B′,然后将两圆的圆
心固定在一起。
2、将其中的一个圆旋转一个角度,使得O A与O′A′重合。
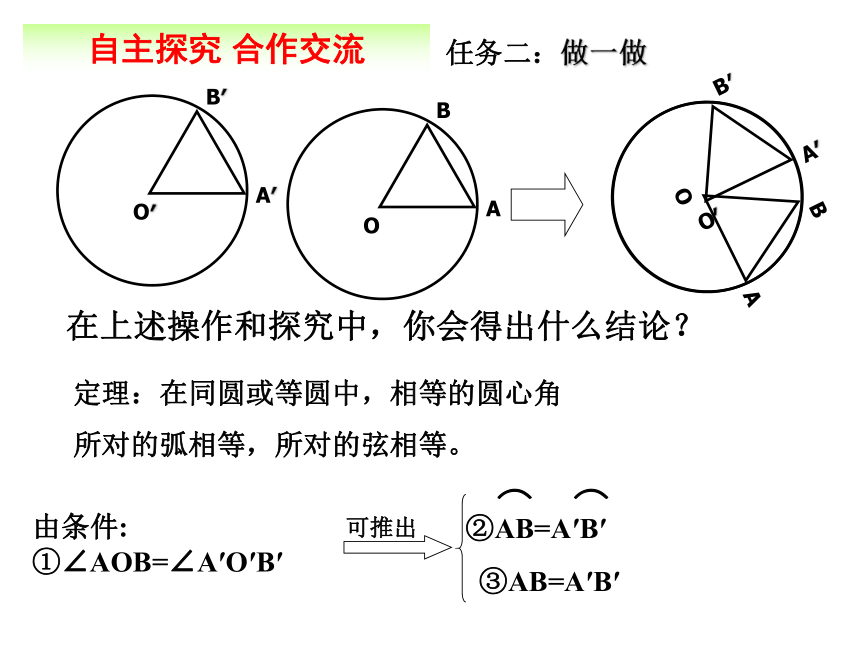
自主探究 合作交流任务二:做一做 你能发现那些等量关系?说一说你的理由.自主探究 合作交流任务二:做一做在上述操作和探究中,你会得出什么结论?定理:在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦相等。 由条件:
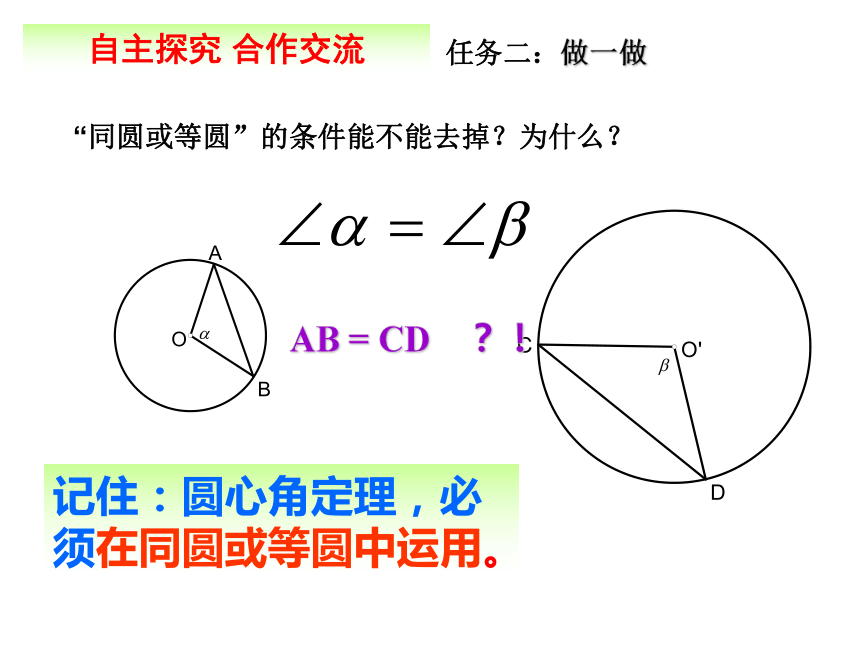
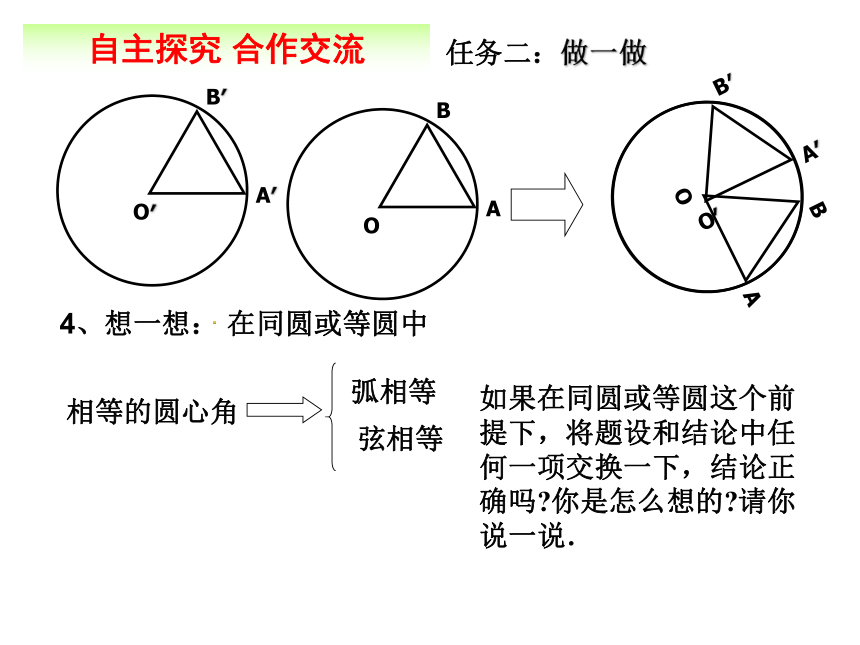
①∠AOB=∠A′O′B′③AB=A′B′AB = CD ?!自主探究 合作交流任务二:做一做“同圆或等圆”的条件能不能去掉?为什么?记住:圆心角定理,必须在同圆或等圆中运用。自主探究 合作交流任务二:做一做4、想一想: 在同圆或等圆中相等的圆心角弧相等弦相等如果在同圆或等圆这个前提下,将题设和结论中任何一项交换一下,结论正确吗?你是怎么想的?请你说一说. 推理格式:自主探究 合作交流任务二:做一做自主探究 合作交流任务二:做一做探索总结定理:在同圆或等圆中,如果两个圆
心角、两条弧、两条弦中有一组量相
等,那么它们所对应的其余各组量都
分别相等。
自主探究 合作交流任务二:做一做自主探究 合作交流任务三:学以致用1、如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么 , 。=(3)如果∠AOB=∠COD,那么 , 。
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?(2)如果,那么 , 。 因为AB=CD ,所以∠AOB=∠COD. 又因为AO=CO,BO=DO, 所以△AOB ≌ △COD. 又因为OE 、OF是AB与CD对应边上的高,所以 OE = OF.2、如图,AB,DE是⊙O的直径,C是⊙O的一点,且,BE与CE的大小有什么关系?为什么?自主探究 合作交流任务三:学以致用课时小结1.在得出本节结论的过程中你用到了哪些
方法?有哪些收获和我们共享? 利用折叠法研究了圆是轴对称图
形;利用旋转的方法得到了圆的旋转不变性,
由圆的旋转不变性,我们探究了圆心角、弧、
弦、弦心距之间相等关系定理。2、你还有什么不理解的地方,需要老师或同学帮助?生命之灯因热情而点
燃,生命之舟因拼搏
而前行拥有梦想是
一种智力,
实现梦想是
一种能力成功的人做别人不愿做
的事,做别人不敢做的
事,做别人做不到的事。快乐是一种心
态,不是一种
状态。奉献使心灵富有,
创造让人生美丽。选择你喜欢的一句话进入冲关1.下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴当堂练习 检测固学2.下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等所对的圆心角相等
当堂练习 检测固学3.下列命题中,不正确的是( )
A.圆是轴对称图形
B.圆是中心对称图形
C.圆既是轴对称图形,又是中心对称图形
D.以上都不对
当堂练习 检测固学·ABCO4. 如图在⊙O中,AB=AC ,∠ABC=60°,
求证:∠AOB=∠BOC=∠AOC.⌒⌒当堂练习 检测固学5.如图,AB、AC、BC都是⊙O的弦,∠AOC=∠BOC.∠ABC与∠BAC相等吗?为什么?当堂练习 检测固学
作业:
课本 第 72页 1,3
变不了过去,那就改变未来。金塔县第四中学 马晓艳九年级数学(下)第三章: 圆第二节 圆的对称性
1、举例说明什么是弧、弦及圆心角。
2、圆是轴对称图形吗?你是怎么验证的?自主预习,认真准备圆是轴对称图形,对称轴有无数条(所有经过圆心的直线都是对称轴)1、判别下列各图中的角是不是圆心角,
并说明理由。①②③④ 请同学们观察屏幕上两个半径相等的圆。请回答: 它们能重合吗?如果能重合,请将它们的圆心
固定在一起。 然后将其中一个圆旋转任意一个角度,这时两个
圆还重合吗 ?圆具有旋转不变性,即一个圆绕着它的圆心
旋转任意一个角度,都能与原来的圆重合。
即因此,圆是中心对称圆形,对称中心为圆
心。圆的中心对称性是其旋转不变性的特例.自主探究 合作交流任务一:探究圆的旋转不变性按下面的步骤做一做
1、利用手中已准备的两张半径相等的透明圆胶片,在⊙O 和⊙O′
上分别作相等的圆心角 ∠A O B和∠A′O′B′,然后将两圆的圆
心固定在一起。
2、将其中的一个圆旋转一个角度,使得O A与O′A′重合。
自主探究 合作交流任务二:做一做 你能发现那些等量关系?说一说你的理由.自主探究 合作交流任务二:做一做在上述操作和探究中,你会得出什么结论?定理:在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦相等。 由条件:
①∠AOB=∠A′O′B′③AB=A′B′AB = CD ?!自主探究 合作交流任务二:做一做“同圆或等圆”的条件能不能去掉?为什么?记住:圆心角定理,必须在同圆或等圆中运用。自主探究 合作交流任务二:做一做4、想一想: 在同圆或等圆中相等的圆心角弧相等弦相等如果在同圆或等圆这个前提下,将题设和结论中任何一项交换一下,结论正确吗?你是怎么想的?请你说一说. 推理格式:自主探究 合作交流任务二:做一做自主探究 合作交流任务二:做一做探索总结定理:在同圆或等圆中,如果两个圆
心角、两条弧、两条弦中有一组量相
等,那么它们所对应的其余各组量都
分别相等。
自主探究 合作交流任务二:做一做自主探究 合作交流任务三:学以致用1、如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么 , 。=(3)如果∠AOB=∠COD,那么 , 。
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?(2)如果,那么 , 。 因为AB=CD ,所以∠AOB=∠COD. 又因为AO=CO,BO=DO, 所以△AOB ≌ △COD. 又因为OE 、OF是AB与CD对应边上的高,所以 OE = OF.2、如图,AB,DE是⊙O的直径,C是⊙O的一点,且,BE与CE的大小有什么关系?为什么?自主探究 合作交流任务三:学以致用课时小结1.在得出本节结论的过程中你用到了哪些
方法?有哪些收获和我们共享? 利用折叠法研究了圆是轴对称图
形;利用旋转的方法得到了圆的旋转不变性,
由圆的旋转不变性,我们探究了圆心角、弧、
弦、弦心距之间相等关系定理。2、你还有什么不理解的地方,需要老师或同学帮助?生命之灯因热情而点
燃,生命之舟因拼搏
而前行拥有梦想是
一种智力,
实现梦想是
一种能力成功的人做别人不愿做
的事,做别人不敢做的
事,做别人做不到的事。快乐是一种心
态,不是一种
状态。奉献使心灵富有,
创造让人生美丽。选择你喜欢的一句话进入冲关1.下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴当堂练习 检测固学2.下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等所对的圆心角相等
当堂练习 检测固学3.下列命题中,不正确的是( )
A.圆是轴对称图形
B.圆是中心对称图形
C.圆既是轴对称图形,又是中心对称图形
D.以上都不对
当堂练习 检测固学·ABCO4. 如图在⊙O中,AB=AC ,∠ABC=60°,
求证:∠AOB=∠BOC=∠AOC.⌒⌒当堂练习 检测固学5.如图,AB、AC、BC都是⊙O的弦,∠AOC=∠BOC.∠ABC与∠BAC相等吗?为什么?当堂练习 检测固学
作业:
课本 第 72页 1,3
