北师大版九年级数学下3.7切线长定理课件(共22张PPT)
文档属性
| 名称 | 北师大版九年级数学下3.7切线长定理课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 108.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-12 11:30:18 | ||
图片预览






文档简介
课件22张PPT。第三章 圆3.7 切线长定理 银川三中 徐秋云一、探究定义1、过⊙O外一点P做圆的切线,能做几条自己动手尝试 2、刚才同学们画出的圆的切线是什么线? 切线长定义:从圆外一点可以引圆的两条切线,这一点和切点之间线段的长度叫做圆的切线长线段PA,PB是点P到⊙O的切线长1、如图, PA和PB分别与⊙O相切于点A、B ,点P到⊙O的切线长可以用哪一条线段的长来表示?2、思考:点P到⊙O的
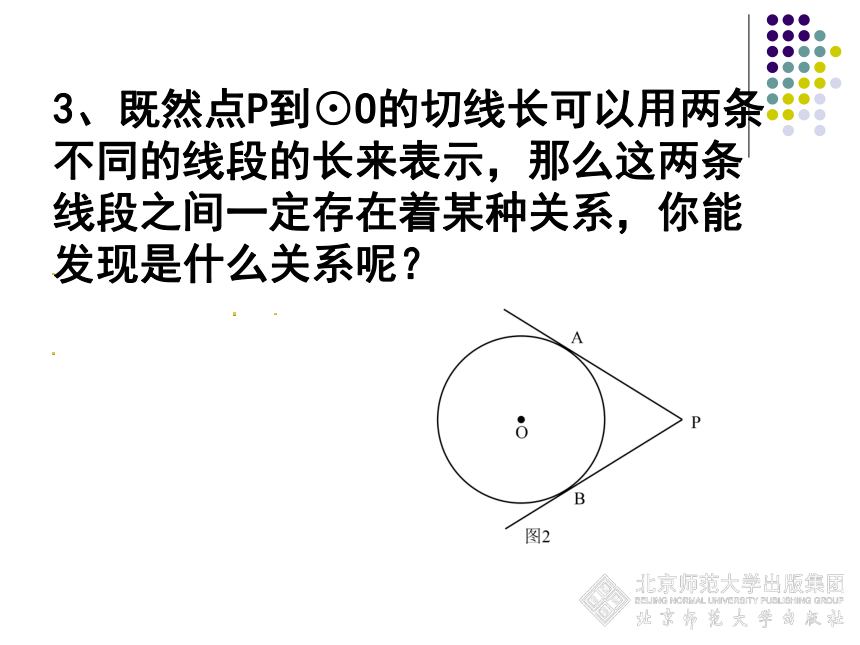
切线有几条?思考???3、既然点P到⊙O的切线长可以用两条不同的线段的长来表示,那么这两条线段之间一定存在着某种关系,你能发现是什么关系呢?
二、探索定理问题1、从⊙O外一点P引⊙O的两条切
线,切点分别为A、B,那么线段PA和
PB之间有何关系?问题2:我们度量猜测的结果能
否作为定理来用呢?为了让我们得出
的命题成为定理,我们需要做什么?已知:PA、PB分别是⊙O的切线,点A、B分别为切点
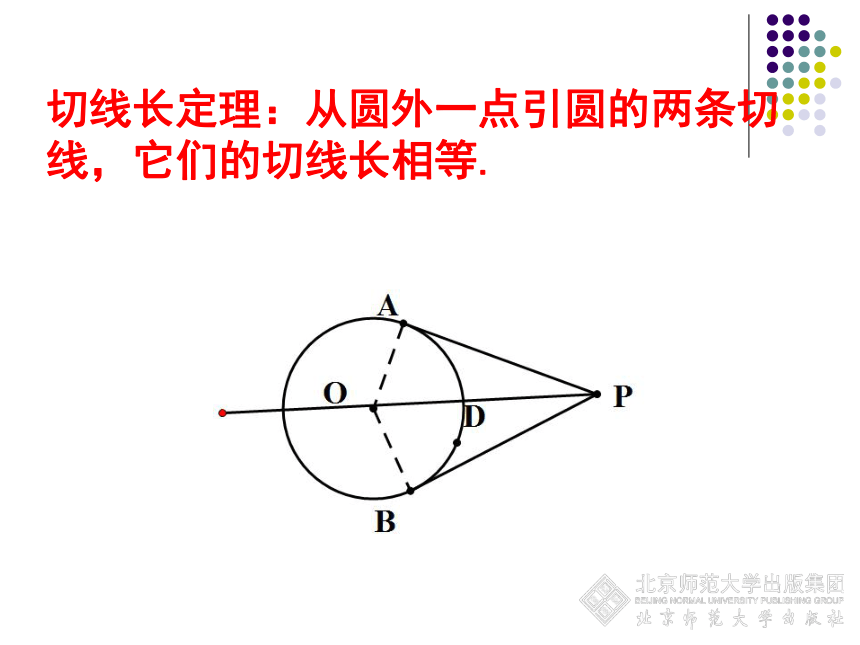
求证:PA=PB切线长定理:从圆外一点引圆的两条切线,它们的切线长相等.三、定理拓展问题:4如果有一张三角形的铁皮,如何在
它的上面截下一块圆形的用料,并且使圆
的面积尽可能最大? 问题5:请同学们先在课堂练习本上作
出有关已知⊙O的四条切线,如图9,
再互相交流与讨论四条切线围成的
四边形(即圆的外切四边形)有什么
性质,发现结论并加以证明。结论:圆的外切四边
形的两组对边的和相等.四、 知识巩固例:已知如图,Rt△ABC的两条直角边
AC=10,BC=24,⊙O 是△ABC 的内切圆,
切点分别为D,E,F,求⊙O 的半径.练习1:已知:如图,△ABC的内切圆
⊙O与BC,CA,AB分别相切于点 D,E,F,
且AB=9cm,BC=14cm,CA=13cm,
求AF,BD,CE的长.
练习2:如图,P是⊙O外一点,PA与
PB分别⊙O切于A.B两点,DE也是⊙O的
切线,切点为C,PA=PB=5cm,
求△PDE的周长.练习3:填空:如图10,PA、PB分别与
⊙O相切于点A、B,
(1)若PB=12,PO=13,则AO=
(2)若PO=10,AO=6,则PB=
(3)若PA=4,AO=3,
则PO= ;
PD= ;
练习4:已知,如图10,PA、PB分别
与⊙O相切于点A、B,PO与⊙O相交于
点D,且PA=4cm,PD=2cm.求半径OA的长.练习5:为了测量一个圆形锅盖的半径,某同学采用了如下办法:将锅盖平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按图中所示的方法得到相关数据,进而可求得锅盖的半径,若测得PA=5cm,则锅盖的半径长是多少?
五、小结回顾1、切线长定理的内容是什么?
2、应用切线长定理解决问题时要注意什么?
3、通过本节课的学习,你学到了哪些学习方法和学习技巧?A层:1.已知:如图,⊙O是△ABC的内
切圆,切点分别为D、E、F,
(1)图中共有几对相等线段?
(2)若AF=4,BD=6,CE=8,则
△ABC的周长是 ;
(3)若AB=9,BC=15,AC=12,则
AF= ,BD= ,CE= .
2.如图,PA、PB分别切⊙O于A、B两点,
C是弧AB上任意一点,过C作⊙O的切线,交PA及PB于D、E两点,已知∠P=50°,PA=PB=6cm,则∠DOE= ,△PDE的周长是 .B层:
1、如图,过⊙O外一点作⊙O的切线
PA、PB,A、B为切点,C为弧AB 上一点,
设∠APB=
求证:∠ACB=.2.如图,PA、PB切⊙O于A、B,
PO交AB于E,等式①AE=BE;
②AO2=OE·OP;③∠OAB=∠APB;
④PA=PB中,成立的有( )
A.1个 B.2个 C.3个 D.4个
切线有几条?思考???3、既然点P到⊙O的切线长可以用两条不同的线段的长来表示,那么这两条线段之间一定存在着某种关系,你能发现是什么关系呢?
二、探索定理问题1、从⊙O外一点P引⊙O的两条切
线,切点分别为A、B,那么线段PA和
PB之间有何关系?问题2:我们度量猜测的结果能
否作为定理来用呢?为了让我们得出
的命题成为定理,我们需要做什么?已知:PA、PB分别是⊙O的切线,点A、B分别为切点
求证:PA=PB切线长定理:从圆外一点引圆的两条切线,它们的切线长相等.三、定理拓展问题:4如果有一张三角形的铁皮,如何在
它的上面截下一块圆形的用料,并且使圆
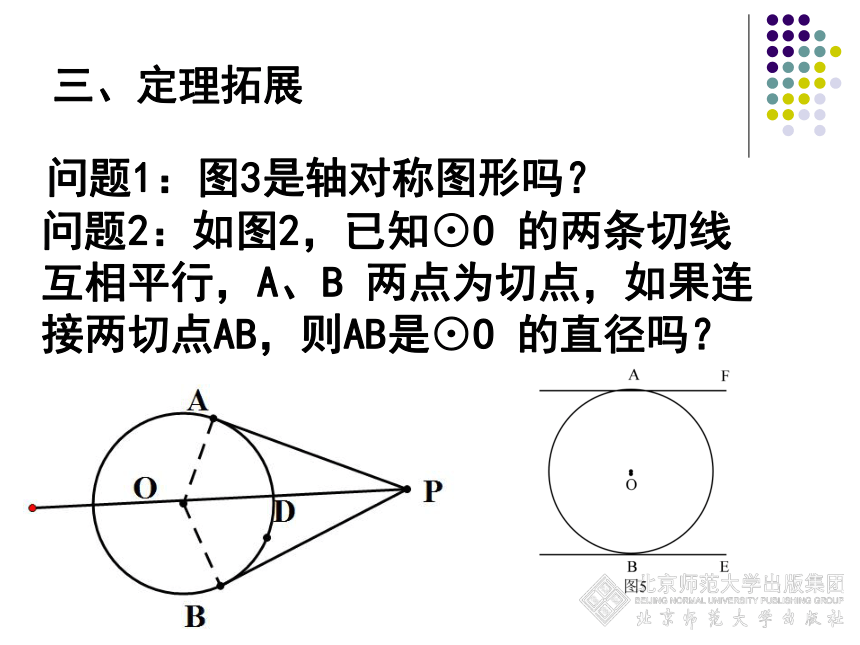
的面积尽可能最大? 问题5:请同学们先在课堂练习本上作
出有关已知⊙O的四条切线,如图9,
再互相交流与讨论四条切线围成的
四边形(即圆的外切四边形)有什么
性质,发现结论并加以证明。结论:圆的外切四边
形的两组对边的和相等.四、 知识巩固例:已知如图,Rt△ABC的两条直角边
AC=10,BC=24,⊙O 是△ABC 的内切圆,
切点分别为D,E,F,求⊙O 的半径.练习1:已知:如图,△ABC的内切圆
⊙O与BC,CA,AB分别相切于点 D,E,F,
且AB=9cm,BC=14cm,CA=13cm,
求AF,BD,CE的长.
练习2:如图,P是⊙O外一点,PA与
PB分别⊙O切于A.B两点,DE也是⊙O的
切线,切点为C,PA=PB=5cm,
求△PDE的周长.练习3:填空:如图10,PA、PB分别与
⊙O相切于点A、B,
(1)若PB=12,PO=13,则AO=
(2)若PO=10,AO=6,则PB=
(3)若PA=4,AO=3,
则PO= ;
PD= ;
练习4:已知,如图10,PA、PB分别
与⊙O相切于点A、B,PO与⊙O相交于
点D,且PA=4cm,PD=2cm.求半径OA的长.练习5:为了测量一个圆形锅盖的半径,某同学采用了如下办法:将锅盖平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按图中所示的方法得到相关数据,进而可求得锅盖的半径,若测得PA=5cm,则锅盖的半径长是多少?
五、小结回顾1、切线长定理的内容是什么?
2、应用切线长定理解决问题时要注意什么?
3、通过本节课的学习,你学到了哪些学习方法和学习技巧?A层:1.已知:如图,⊙O是△ABC的内
切圆,切点分别为D、E、F,
(1)图中共有几对相等线段?
(2)若AF=4,BD=6,CE=8,则
△ABC的周长是 ;
(3)若AB=9,BC=15,AC=12,则
AF= ,BD= ,CE= .
2.如图,PA、PB分别切⊙O于A、B两点,
C是弧AB上任意一点,过C作⊙O的切线,交PA及PB于D、E两点,已知∠P=50°,PA=PB=6cm,则∠DOE= ,△PDE的周长是 .B层:
1、如图,过⊙O外一点作⊙O的切线
PA、PB,A、B为切点,C为弧AB 上一点,
设∠APB=
求证:∠ACB=.2.如图,PA、PB切⊙O于A、B,
PO交AB于E,等式①AE=BE;
②AO2=OE·OP;③∠OAB=∠APB;
④PA=PB中,成立的有( )
A.1个 B.2个 C.3个 D.4个
