【期末专项培优】平均数(含解析)2024-2025学年华东师大版数学八年级下册
文档属性
| 名称 | 【期末专项培优】平均数(含解析)2024-2025学年华东师大版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 246.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 15:30:04 | ||
图片预览




文档简介
期末专项培优 平均数
一.选择题(共5小题)
1.(2024秋 化州市期末)某招聘考试要进行笔试和面试,其中笔试占60%,面试占40%.孔明笔试成绩90分,面试成绩80分,那么孔明的最后成绩是( )
A.90分 B.88分 C.86分 D.80分
2.(2024秋 郑州期末)某校举办“身边的温暖故事”主题演讲比赛,其中前三名选手的成绩统计如表.
选手 评分项目
故事内容(单位:分) 情感表达(单位:分) 演讲技巧(单位:分)
小琪 100 85 90
小清 79 100 100
小明 95 90 90
若故事内容、情感表达、演讲技巧按4:3:3的加权平均分决定冠军、亚军、季军,则冠军、亚军、季军分别是( )
A.小清、小明、小琪 B.小清、小琪、小明
C.小琪、小明、小清 D.小琪、小清、小明
3.(2024秋 高州市期末)“双减”政策落地,各地学校为了提升学生核心素养,把学生的综合评价分为学习、体育和艺术三部分,学习成绩、体育成绩与艺术成绩按5:3:2计入综合评价.若珊珊学习成绩为90分,体育成绩为80分,艺术成绩为70分,则他的综合评价得分为( )
A.84 B.85 C.82 D.83
4.(2024秋 福田区期末)某校举行校园十佳歌手大赛,小颖同学的初赛成绩为90分,复赛成绩为80分.若总成绩按初赛成绩占30%,复赛成绩占70%来计算,则小颖同学的总成绩为( )
A.83分 B.80分 C.75分 D.70分
5.(2024秋 太仓市期末)已知五个数据:2,2,x,5,8的平均数是4,现增加了一个数据后的平均数仍不变,则增加的这个数据是( )
A.0 B.2 C.4 D.5
二.填空题(共5小题)
6.(2024秋 茂名期末)公司对应聘者进行创新、综合知识、语言测试,三项成绩分别为72分、50分、88分.若这三项测试得分依次按5:2:1的比例确定个人的综合成绩,则该应聘者的得分为 分.
7.(2024秋 兰州期末)数据﹣2,0,1,﹣2,﹣2的平均数是 .
8.(2024秋 中卫期末)2024年4月23日是第29个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算.小芳这四项的得分依次为85,95,92,88,则她的最后得分是 分.
9.(2024秋 西安期末)如图是某校学生年龄分布情况统计图,根据统计图计算该校学生的平均年龄为 .
10.(2024秋 碑林区校级期末)某校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小明的平时、期末成绩分别为85分,95分,则小明本学期的学业成绩为 分.
三.解答题(共5小题)
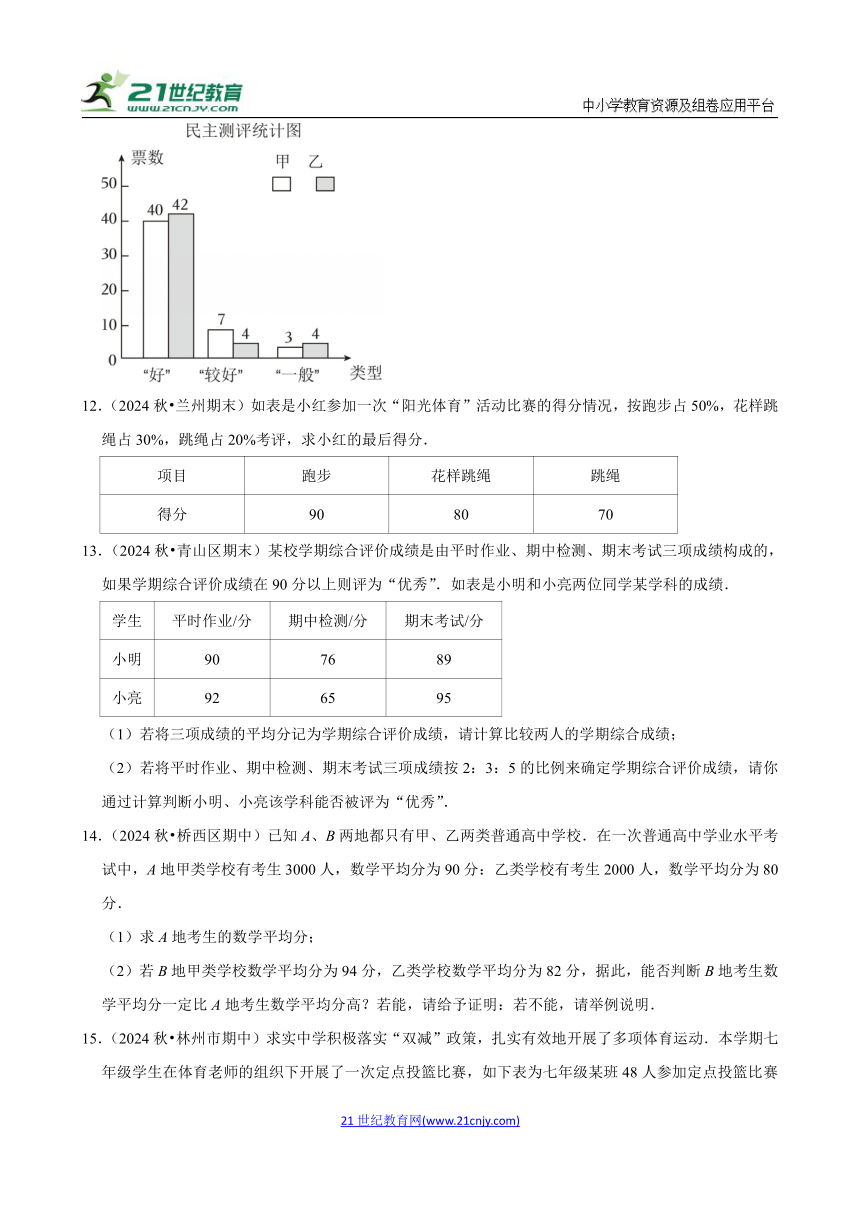
11.(2024秋 源城区期末)某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
12.(2024秋 兰州期末)如表是小红参加一次“阳光体育”活动比赛的得分情况,按跑步占50%,花样跳绳占30%,跳绳占20%考评,求小红的最后得分.
项目 跑步 花样跳绳 跳绳
得分 90 80 70
13.(2024秋 青山区期末)某校学期综合评价成绩是由平时作业、期中检测、期末考试三项成绩构成的,如果学期综合评价成绩在90分以上则评为“优秀”.如表是小明和小亮两位同学某学科的成绩.
学生 平时作业/分 期中检测/分 期末考试/分
小明 90 76 89
小亮 92 65 95
(1)若将三项成绩的平均分记为学期综合评价成绩,请计算比较两人的学期综合成绩;
(2)若将平时作业、期中检测、期末考试三项成绩按2:3:5的比例来确定学期综合评价成绩,请你通过计算判断小明、小亮该学科能否被评为“优秀”.
14.(2024秋 桥西区期中)已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
15.(2024秋 林州市期中)求实中学积极落实“双减”政策,扎实有效地开展了多项体育运动.本学期七年级学生在体育老师的组织下开展了一次定点投篮比赛,如下表为七年级某班48人参加定点投篮比赛的情况记录,若标准数量为每人三分钟定点投篮投中25个.
定点投篮投中个数与标准数量的差值 ﹣11 ﹣6 0 8 10
人数 5 12 10 6 10
(1)该班平均每人三分钟定点投篮投中多少个?
(2)规定定点投篮投中个数达到标准数量记0分,超过标准数量,每多投1个加2分,每少投1个扣1分,求该班定点投篮总共获得多少分?
期末专项培优 平均数
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 化州市期末)某招聘考试要进行笔试和面试,其中笔试占60%,面试占40%.孔明笔试成绩90分,面试成绩80分,那么孔明的最后成绩是( )
A.90分 B.88分 C.86分 D.80分
【考点】加权平均数.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】利用加权平均数计算方法计算即可.
【解答】解:由题意得:
86(分),
故选:C.
【点评】此题主要考查了加权平均数,关键是掌握加权平均数计算公式.
2.(2024秋 郑州期末)某校举办“身边的温暖故事”主题演讲比赛,其中前三名选手的成绩统计如表.
选手 评分项目
故事内容(单位:分) 情感表达(单位:分) 演讲技巧(单位:分)
小琪 100 85 90
小清 79 100 100
小明 95 90 90
若故事内容、情感表达、演讲技巧按4:3:3的加权平均分决定冠军、亚军、季军,则冠军、亚军、季军分别是( )
A.小清、小明、小琪 B.小清、小琪、小明
C.小琪、小明、小清 D.小琪、小清、小明
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】C
【分析】根据加权平均数的定义分别计算出三人的平均成绩,再比较大小即可得出答案.
【解答】解:小琪的平均成绩为92.5(分),
小清的平均成绩为91.6(分),
小明的平均成绩为92(分),
92.5>92>91.6,
所以冠军、亚军、季军分别是小琪、小明、小清.
故选:C.
【点评】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
3.(2024秋 高州市期末)“双减”政策落地,各地学校为了提升学生核心素养,把学生的综合评价分为学习、体育和艺术三部分,学习成绩、体育成绩与艺术成绩按5:3:2计入综合评价.若珊珊学习成绩为90分,体育成绩为80分,艺术成绩为70分,则他的综合评价得分为( )
A.84 B.85 C.82 D.83
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】D
【分析】根据加权平均数的定义列式计算即可.
【解答】解:根据题意,他的综合评价得分为83(分).
故选:D.
【点评】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
4.(2024秋 福田区期末)某校举行校园十佳歌手大赛,小颖同学的初赛成绩为90分,复赛成绩为80分.若总成绩按初赛成绩占30%,复赛成绩占70%来计算,则小颖同学的总成绩为( )
A.83分 B.80分 C.75分 D.70分
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】A
【分析】根据加权平均数计算公式列出算式,再进行计算即可得出答案.
【解答】解:小颖同学的总成绩为90×30%+80×70%=83(分).
故选:A.
【点评】本题主要考查加权平均数,熟练掌握加权平均数的定义是解题的关键.
5.(2024秋 太仓市期末)已知五个数据:2,2,x,5,8的平均数是4,现增加了一个数据后的平均数仍不变,则增加的这个数据是( )
A.0 B.2 C.4 D.5
【考点】算术平均数.
【专题】统计的应用;数据分析观念.
【答案】C
【分析】先根据算术平均数的定义求出x的值,再设增加数据为m,由增加了一个数据后的平均数仍不变列出关于m的方程,解之即可得出答案.
【解答】解:由题意知,4,
解得x=3,
所以原数据为2、2、3、5、8,
设增加数据为m,
则4,
解得m=4,
故选:C.
【点评】本题主要考查算术平均数,解题的关键是掌握算术平均数的定义.
二.填空题(共5小题)
6.(2024秋 茂名期末)公司对应聘者进行创新、综合知识、语言测试,三项成绩分别为72分、50分、88分.若这三项测试得分依次按5:2:1的比例确定个人的综合成绩,则该应聘者的得分为 68.5 分.
【考点】加权平均数.
【专题】统计的应用;数据分析观念.
【答案】68.5.
【分析】把各项成绩分别乘以其权,再除以权的和,即可求出加权平均数.
【解答】解:(分),
故答案为:68.5.
【点评】本题考查了加权平均数,熟练掌握定义是解题的关键.
7.(2024秋 兰州期末)数据﹣2,0,1,﹣2,﹣2的平均数是 ﹣1 .
【考点】算术平均数.
【专题】统计的应用;数据分析观念.
【答案】﹣1.
【分析】将题目中的数据相加,然后除以5,即可得到这组数据的平均数.
【解答】解:(﹣2+0+1﹣2﹣2)÷5
=(﹣5)÷5
=﹣1,
∴数据﹣2,0,1,﹣2,﹣2的平均数是﹣1,
故答案为:﹣1.
【点评】本题考查算术平均数,解答本题的关键是明确算术平均数的计算方法.
8.(2024秋 中卫期末)2024年4月23日是第29个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算.小芳这四项的得分依次为85,95,92,88,则她的最后得分是 90 分.
【考点】加权平均数.
【专题】运算能力.
【答案】90.
【分析】根据加权平均数的定义列式计算可得.
【解答】解:她的最后得分是85×40%+95×40%+92×10%+88×10%=90(分),
故答案为:90.
【点评】本题考查的是加权平均数的求法,熟练掌握加权平均数的计算公式是解题的关键.
9.(2024秋 西安期末)如图是某校学生年龄分布情况统计图,根据统计图计算该校学生的平均年龄为 13.95岁 .
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】见试题解答内容
【分析】根据加权平均数的计算公式列出算式,再进行计算即可得出答案.
【解答】解:根据题意得:
12×15%+13×20%+14×30%+15×25%+16×10%=13.95(岁),
答:该校学生的平均年龄为13.95岁.
故答案为:13.95岁.
【点评】此题考查了加权平均数,熟练掌握加权平均数的计算公式是解题的关键.
10.(2024秋 碑林区校级期末)某校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小明的平时、期末成绩分别为85分,95分,则小明本学期的学业成绩为 91 分.
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】91.
【分析】根据加权平均数的计算方法计算即可.
【解答】解:小明本学期的学业成绩为:85×40%+95×60%=34+57=91(分).
故答案为:91.
【点评】本题主要考查加权平均数,熟练掌握加权平均数的计算方法是解题的关键.
三.解答题(共5小题)
11.(2024秋 源城区期末)某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
【考点】加权平均数.
【专题】数据的收集与整理;应用意识.
【答案】(1)甲演讲答辩平均分为92分,乙演讲答辩平均分为89分;
(2)甲民主测评得分为87分,乙民主测评得分为88分.
(3)应选甲同学当班长.
【分析】(1)每个选手去掉一个最高分,再去掉一个最低分,求出剩下三个数的平均数即可;
(2)分别求出甲乙的民主测评得分即可.
(3)根据加权平均数的公式,计算即可判断.
【解答】解:(1)甲演讲答辩平均分92(分),
乙演讲答辩平均分:89(分),
(2)甲民主测评得分:40×2+7×1=87(分),
乙民主测评得分,42×2+4×1=88(分).
(4)甲综合得分90(分),
乙综合得分88.6(分),
∵90>88.6,
∴应选甲同学当班长.
【点评】本题考查了平均数和加权平均数的概念及应用,以及从统计图中获取信息的能力.解题的关键是理解题意,理解“权”对平均数的影响.
12.(2024秋 兰州期末)如表是小红参加一次“阳光体育”活动比赛的得分情况,按跑步占50%,花样跳绳占30%,跳绳占20%考评,求小红的最后得分.
项目 跑步 花样跳绳 跳绳
得分 90 80 70
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】83分.
【分析】根据加权平均数的计算公式进行计算即可.
【解答】解:90×50%+80×30%+70×20%=83(分),
答:小红的最后得分为83分.
【点评】本题考查的是加权平均数,熟记加权平均数的计算公式是解决本题的关键.
13.(2024秋 青山区期末)某校学期综合评价成绩是由平时作业、期中检测、期末考试三项成绩构成的,如果学期综合评价成绩在90分以上则评为“优秀”.如表是小明和小亮两位同学某学科的成绩.
学生 平时作业/分 期中检测/分 期末考试/分
小明 90 76 89
小亮 92 65 95
(1)若将三项成绩的平均分记为学期综合评价成绩,请计算比较两人的学期综合成绩;
(2)若将平时作业、期中检测、期末考试三项成绩按2:3:5的比例来确定学期综合评价成绩,请你通过计算判断小明、小亮该学科能否被评为“优秀”.
【考点】加权平均数.
【专题】统计的应用;数据分析观念.
【答案】(1)小明的学期综合评价成绩为比小亮的学期综合评价成绩好.
(2)小明和小亮该学科不能被评为“优秀”.
【分析】(1)根据平均数的定义,将三个成绩之和除以3即可求解;
(2)根据加权平均数的定义即可求解.
【解答】解:(1)(90+76+89)=85(分),
∴小明的学期综合评价成绩为85分;
84(分),
∴小亮的学期综合评价成绩为85分;
∴小明的学期综合评价成绩为比小亮的学期综合评价成绩好.
(2)由题意,85.3,
小明在期末考试中的成绩是85.3分,
85.4(分),
∴小亮在期末考试中的成绩是85.4分,
∵学期综合评价成绩在90分以上则评为“优秀”,
∴小明和小亮该学科不能被评为“优秀”.
【点评】本题考查算术平均数与加权平均数,掌握平均数和加权平均数的求法是解题的关键.
14.(2024秋 桥西区期中)已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
【考点】加权平均数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)86分;
(2)不能,举例见解析.
【分析】(1)根据平均数的概念求解即可;
(2)根据平均数的意义求解即可.
【解答】解:(1)由题意,得A地考生的数学平均分为(分);
(2)不能.举例如下:
如B地甲类学校有考生1000人,乙类学校有考生3000人,则B地考生的数学平均分为
(分),
∵85<86,
∴不能判断B地考生数学平均分一定比A地考生数学平均分高.
【点评】本题考查加权平均数等基础知识,掌握加权平均数是解题的关键.
15.(2024秋 林州市期中)求实中学积极落实“双减”政策,扎实有效地开展了多项体育运动.本学期七年级学生在体育老师的组织下开展了一次定点投篮比赛,如下表为七年级某班48人参加定点投篮比赛的情况记录,若标准数量为每人三分钟定点投篮投中25个.
定点投篮投中个数与标准数量的差值 ﹣11 ﹣6 0 8 10
人数 5 12 10 6 10
(1)该班平均每人三分钟定点投篮投中多少个?
(2)规定定点投篮投中个数达到标准数量记0分,超过标准数量,每多投1个加2分,每少投1个扣1分,求该班定点投篮总共获得多少分?
【考点】加权平均数;正数和负数;有理数的减法.
【专题】计算题;运算能力.
【答案】(1)25.4375个;(2)169分.
【分析】(1)先求该班总和,再求平均每人三分钟定点投篮投中的个数;
(2)用该班定点投篮总共获得分等于加分减扣分即可.
【解答】解:(1)该班平均每人三分钟定点投篮投中[0×10+8×6+10×10﹣11×5﹣6×12]÷48+25=25.4375个;
(2)该班定点投篮总共获得[8×6+10×10]×2﹣[11×5﹣+6×12]×1=169分.
【点评】本题主要考查了加权平均数,解题关键是正确计算.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 化州市期末)某招聘考试要进行笔试和面试,其中笔试占60%,面试占40%.孔明笔试成绩90分,面试成绩80分,那么孔明的最后成绩是( )
A.90分 B.88分 C.86分 D.80分
2.(2024秋 郑州期末)某校举办“身边的温暖故事”主题演讲比赛,其中前三名选手的成绩统计如表.
选手 评分项目
故事内容(单位:分) 情感表达(单位:分) 演讲技巧(单位:分)
小琪 100 85 90
小清 79 100 100
小明 95 90 90
若故事内容、情感表达、演讲技巧按4:3:3的加权平均分决定冠军、亚军、季军,则冠军、亚军、季军分别是( )
A.小清、小明、小琪 B.小清、小琪、小明
C.小琪、小明、小清 D.小琪、小清、小明
3.(2024秋 高州市期末)“双减”政策落地,各地学校为了提升学生核心素养,把学生的综合评价分为学习、体育和艺术三部分,学习成绩、体育成绩与艺术成绩按5:3:2计入综合评价.若珊珊学习成绩为90分,体育成绩为80分,艺术成绩为70分,则他的综合评价得分为( )
A.84 B.85 C.82 D.83
4.(2024秋 福田区期末)某校举行校园十佳歌手大赛,小颖同学的初赛成绩为90分,复赛成绩为80分.若总成绩按初赛成绩占30%,复赛成绩占70%来计算,则小颖同学的总成绩为( )
A.83分 B.80分 C.75分 D.70分
5.(2024秋 太仓市期末)已知五个数据:2,2,x,5,8的平均数是4,现增加了一个数据后的平均数仍不变,则增加的这个数据是( )
A.0 B.2 C.4 D.5
二.填空题(共5小题)
6.(2024秋 茂名期末)公司对应聘者进行创新、综合知识、语言测试,三项成绩分别为72分、50分、88分.若这三项测试得分依次按5:2:1的比例确定个人的综合成绩,则该应聘者的得分为 分.
7.(2024秋 兰州期末)数据﹣2,0,1,﹣2,﹣2的平均数是 .
8.(2024秋 中卫期末)2024年4月23日是第29个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算.小芳这四项的得分依次为85,95,92,88,则她的最后得分是 分.
9.(2024秋 西安期末)如图是某校学生年龄分布情况统计图,根据统计图计算该校学生的平均年龄为 .
10.(2024秋 碑林区校级期末)某校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小明的平时、期末成绩分别为85分,95分,则小明本学期的学业成绩为 分.
三.解答题(共5小题)
11.(2024秋 源城区期末)某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
12.(2024秋 兰州期末)如表是小红参加一次“阳光体育”活动比赛的得分情况,按跑步占50%,花样跳绳占30%,跳绳占20%考评,求小红的最后得分.
项目 跑步 花样跳绳 跳绳
得分 90 80 70
13.(2024秋 青山区期末)某校学期综合评价成绩是由平时作业、期中检测、期末考试三项成绩构成的,如果学期综合评价成绩在90分以上则评为“优秀”.如表是小明和小亮两位同学某学科的成绩.
学生 平时作业/分 期中检测/分 期末考试/分
小明 90 76 89
小亮 92 65 95
(1)若将三项成绩的平均分记为学期综合评价成绩,请计算比较两人的学期综合成绩;
(2)若将平时作业、期中检测、期末考试三项成绩按2:3:5的比例来确定学期综合评价成绩,请你通过计算判断小明、小亮该学科能否被评为“优秀”.
14.(2024秋 桥西区期中)已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
15.(2024秋 林州市期中)求实中学积极落实“双减”政策,扎实有效地开展了多项体育运动.本学期七年级学生在体育老师的组织下开展了一次定点投篮比赛,如下表为七年级某班48人参加定点投篮比赛的情况记录,若标准数量为每人三分钟定点投篮投中25个.
定点投篮投中个数与标准数量的差值 ﹣11 ﹣6 0 8 10
人数 5 12 10 6 10
(1)该班平均每人三分钟定点投篮投中多少个?
(2)规定定点投篮投中个数达到标准数量记0分,超过标准数量,每多投1个加2分,每少投1个扣1分,求该班定点投篮总共获得多少分?
期末专项培优 平均数
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 化州市期末)某招聘考试要进行笔试和面试,其中笔试占60%,面试占40%.孔明笔试成绩90分,面试成绩80分,那么孔明的最后成绩是( )
A.90分 B.88分 C.86分 D.80分
【考点】加权平均数.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】利用加权平均数计算方法计算即可.
【解答】解:由题意得:
86(分),
故选:C.
【点评】此题主要考查了加权平均数,关键是掌握加权平均数计算公式.
2.(2024秋 郑州期末)某校举办“身边的温暖故事”主题演讲比赛,其中前三名选手的成绩统计如表.
选手 评分项目
故事内容(单位:分) 情感表达(单位:分) 演讲技巧(单位:分)
小琪 100 85 90
小清 79 100 100
小明 95 90 90
若故事内容、情感表达、演讲技巧按4:3:3的加权平均分决定冠军、亚军、季军,则冠军、亚军、季军分别是( )
A.小清、小明、小琪 B.小清、小琪、小明
C.小琪、小明、小清 D.小琪、小清、小明
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】C
【分析】根据加权平均数的定义分别计算出三人的平均成绩,再比较大小即可得出答案.
【解答】解:小琪的平均成绩为92.5(分),
小清的平均成绩为91.6(分),
小明的平均成绩为92(分),
92.5>92>91.6,
所以冠军、亚军、季军分别是小琪、小明、小清.
故选:C.
【点评】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
3.(2024秋 高州市期末)“双减”政策落地,各地学校为了提升学生核心素养,把学生的综合评价分为学习、体育和艺术三部分,学习成绩、体育成绩与艺术成绩按5:3:2计入综合评价.若珊珊学习成绩为90分,体育成绩为80分,艺术成绩为70分,则他的综合评价得分为( )
A.84 B.85 C.82 D.83
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】D
【分析】根据加权平均数的定义列式计算即可.
【解答】解:根据题意,他的综合评价得分为83(分).
故选:D.
【点评】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
4.(2024秋 福田区期末)某校举行校园十佳歌手大赛,小颖同学的初赛成绩为90分,复赛成绩为80分.若总成绩按初赛成绩占30%,复赛成绩占70%来计算,则小颖同学的总成绩为( )
A.83分 B.80分 C.75分 D.70分
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】A
【分析】根据加权平均数计算公式列出算式,再进行计算即可得出答案.
【解答】解:小颖同学的总成绩为90×30%+80×70%=83(分).
故选:A.
【点评】本题主要考查加权平均数,熟练掌握加权平均数的定义是解题的关键.
5.(2024秋 太仓市期末)已知五个数据:2,2,x,5,8的平均数是4,现增加了一个数据后的平均数仍不变,则增加的这个数据是( )
A.0 B.2 C.4 D.5
【考点】算术平均数.
【专题】统计的应用;数据分析观念.
【答案】C
【分析】先根据算术平均数的定义求出x的值,再设增加数据为m,由增加了一个数据后的平均数仍不变列出关于m的方程,解之即可得出答案.
【解答】解:由题意知,4,
解得x=3,
所以原数据为2、2、3、5、8,
设增加数据为m,
则4,
解得m=4,
故选:C.
【点评】本题主要考查算术平均数,解题的关键是掌握算术平均数的定义.
二.填空题(共5小题)
6.(2024秋 茂名期末)公司对应聘者进行创新、综合知识、语言测试,三项成绩分别为72分、50分、88分.若这三项测试得分依次按5:2:1的比例确定个人的综合成绩,则该应聘者的得分为 68.5 分.
【考点】加权平均数.
【专题】统计的应用;数据分析观念.
【答案】68.5.
【分析】把各项成绩分别乘以其权,再除以权的和,即可求出加权平均数.
【解答】解:(分),
故答案为:68.5.
【点评】本题考查了加权平均数,熟练掌握定义是解题的关键.
7.(2024秋 兰州期末)数据﹣2,0,1,﹣2,﹣2的平均数是 ﹣1 .
【考点】算术平均数.
【专题】统计的应用;数据分析观念.
【答案】﹣1.
【分析】将题目中的数据相加,然后除以5,即可得到这组数据的平均数.
【解答】解:(﹣2+0+1﹣2﹣2)÷5
=(﹣5)÷5
=﹣1,
∴数据﹣2,0,1,﹣2,﹣2的平均数是﹣1,
故答案为:﹣1.
【点评】本题考查算术平均数,解答本题的关键是明确算术平均数的计算方法.
8.(2024秋 中卫期末)2024年4月23日是第29个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算.小芳这四项的得分依次为85,95,92,88,则她的最后得分是 90 分.
【考点】加权平均数.
【专题】运算能力.
【答案】90.
【分析】根据加权平均数的定义列式计算可得.
【解答】解:她的最后得分是85×40%+95×40%+92×10%+88×10%=90(分),
故答案为:90.
【点评】本题考查的是加权平均数的求法,熟练掌握加权平均数的计算公式是解题的关键.
9.(2024秋 西安期末)如图是某校学生年龄分布情况统计图,根据统计图计算该校学生的平均年龄为 13.95岁 .
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】见试题解答内容
【分析】根据加权平均数的计算公式列出算式,再进行计算即可得出答案.
【解答】解:根据题意得:
12×15%+13×20%+14×30%+15×25%+16×10%=13.95(岁),
答:该校学生的平均年龄为13.95岁.
故答案为:13.95岁.
【点评】此题考查了加权平均数,熟练掌握加权平均数的计算公式是解题的关键.
10.(2024秋 碑林区校级期末)某校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小明的平时、期末成绩分别为85分,95分,则小明本学期的学业成绩为 91 分.
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】91.
【分析】根据加权平均数的计算方法计算即可.
【解答】解:小明本学期的学业成绩为:85×40%+95×60%=34+57=91(分).
故答案为:91.
【点评】本题主要考查加权平均数,熟练掌握加权平均数的计算方法是解题的关键.
三.解答题(共5小题)
11.(2024秋 源城区期末)某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
【考点】加权平均数.
【专题】数据的收集与整理;应用意识.
【答案】(1)甲演讲答辩平均分为92分,乙演讲答辩平均分为89分;
(2)甲民主测评得分为87分,乙民主测评得分为88分.
(3)应选甲同学当班长.
【分析】(1)每个选手去掉一个最高分,再去掉一个最低分,求出剩下三个数的平均数即可;
(2)分别求出甲乙的民主测评得分即可.
(3)根据加权平均数的公式,计算即可判断.
【解答】解:(1)甲演讲答辩平均分92(分),
乙演讲答辩平均分:89(分),
(2)甲民主测评得分:40×2+7×1=87(分),
乙民主测评得分,42×2+4×1=88(分).
(4)甲综合得分90(分),
乙综合得分88.6(分),
∵90>88.6,
∴应选甲同学当班长.
【点评】本题考查了平均数和加权平均数的概念及应用,以及从统计图中获取信息的能力.解题的关键是理解题意,理解“权”对平均数的影响.
12.(2024秋 兰州期末)如表是小红参加一次“阳光体育”活动比赛的得分情况,按跑步占50%,花样跳绳占30%,跳绳占20%考评,求小红的最后得分.
项目 跑步 花样跳绳 跳绳
得分 90 80 70
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】83分.
【分析】根据加权平均数的计算公式进行计算即可.
【解答】解:90×50%+80×30%+70×20%=83(分),
答:小红的最后得分为83分.
【点评】本题考查的是加权平均数,熟记加权平均数的计算公式是解决本题的关键.
13.(2024秋 青山区期末)某校学期综合评价成绩是由平时作业、期中检测、期末考试三项成绩构成的,如果学期综合评价成绩在90分以上则评为“优秀”.如表是小明和小亮两位同学某学科的成绩.
学生 平时作业/分 期中检测/分 期末考试/分
小明 90 76 89
小亮 92 65 95
(1)若将三项成绩的平均分记为学期综合评价成绩,请计算比较两人的学期综合成绩;
(2)若将平时作业、期中检测、期末考试三项成绩按2:3:5的比例来确定学期综合评价成绩,请你通过计算判断小明、小亮该学科能否被评为“优秀”.
【考点】加权平均数.
【专题】统计的应用;数据分析观念.
【答案】(1)小明的学期综合评价成绩为比小亮的学期综合评价成绩好.
(2)小明和小亮该学科不能被评为“优秀”.
【分析】(1)根据平均数的定义,将三个成绩之和除以3即可求解;
(2)根据加权平均数的定义即可求解.
【解答】解:(1)(90+76+89)=85(分),
∴小明的学期综合评价成绩为85分;
84(分),
∴小亮的学期综合评价成绩为85分;
∴小明的学期综合评价成绩为比小亮的学期综合评价成绩好.
(2)由题意,85.3,
小明在期末考试中的成绩是85.3分,
85.4(分),
∴小亮在期末考试中的成绩是85.4分,
∵学期综合评价成绩在90分以上则评为“优秀”,
∴小明和小亮该学科不能被评为“优秀”.
【点评】本题考查算术平均数与加权平均数,掌握平均数和加权平均数的求法是解题的关键.
14.(2024秋 桥西区期中)已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
【考点】加权平均数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)86分;
(2)不能,举例见解析.
【分析】(1)根据平均数的概念求解即可;
(2)根据平均数的意义求解即可.
【解答】解:(1)由题意,得A地考生的数学平均分为(分);
(2)不能.举例如下:
如B地甲类学校有考生1000人,乙类学校有考生3000人,则B地考生的数学平均分为
(分),
∵85<86,
∴不能判断B地考生数学平均分一定比A地考生数学平均分高.
【点评】本题考查加权平均数等基础知识,掌握加权平均数是解题的关键.
15.(2024秋 林州市期中)求实中学积极落实“双减”政策,扎实有效地开展了多项体育运动.本学期七年级学生在体育老师的组织下开展了一次定点投篮比赛,如下表为七年级某班48人参加定点投篮比赛的情况记录,若标准数量为每人三分钟定点投篮投中25个.
定点投篮投中个数与标准数量的差值 ﹣11 ﹣6 0 8 10
人数 5 12 10 6 10
(1)该班平均每人三分钟定点投篮投中多少个?
(2)规定定点投篮投中个数达到标准数量记0分,超过标准数量,每多投1个加2分,每少投1个扣1分,求该班定点投篮总共获得多少分?
【考点】加权平均数;正数和负数;有理数的减法.
【专题】计算题;运算能力.
【答案】(1)25.4375个;(2)169分.
【分析】(1)先求该班总和,再求平均每人三分钟定点投篮投中的个数;
(2)用该班定点投篮总共获得分等于加分减扣分即可.
【解答】解:(1)该班平均每人三分钟定点投篮投中[0×10+8×6+10×10﹣11×5﹣6×12]÷48+25=25.4375个;
(2)该班定点投篮总共获得[8×6+10×10]×2﹣[11×5﹣+6×12]×1=169分.
【点评】本题主要考查了加权平均数,解题关键是正确计算.
21世纪教育网(www.21cnjy.com)
