【期末专项培优】勾股定理(含解析)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 【期末专项培优】勾股定理(含解析)2024-2025学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 762.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 00:00:00 | ||
图片预览


文档简介
期末专项培优 勾股定理
一.选择题(共5小题)
1.(2024秋 长春校级期末)如图,数轴上点A,B对应的数分别是1,2,以AB为边在数轴上方作正方形ABCD,连接AC,以A为圆心,AC的长为半径画圆弧交数轴于点E(点E在点A的左侧),则点E在数轴上对应的数为( )
A. B. C. D.
2.(2024秋 拱墅区期末)一个直角三角形,若三边的平方和为200,则斜边长为( )
A.8 B.9 C.10 D.11
3.(2024秋 源城区期末)已知一个直角三角形的两条边长分别为和1,则第三边长为( )
A. B.2 C.或2 D.或4
4.(2024秋 建邺区期末)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以各边为直径作半圆,则图中阴影部分的面积为( )
A.6 B. C.4π﹣6 D.
5.(2024秋 滨湖区期末)“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m,n(m>n).若小正方形面积为7,(m+n)2=21,则大正方形面积为( )
A.11 B.12 C.13 D.14
二.填空题(共5小题)
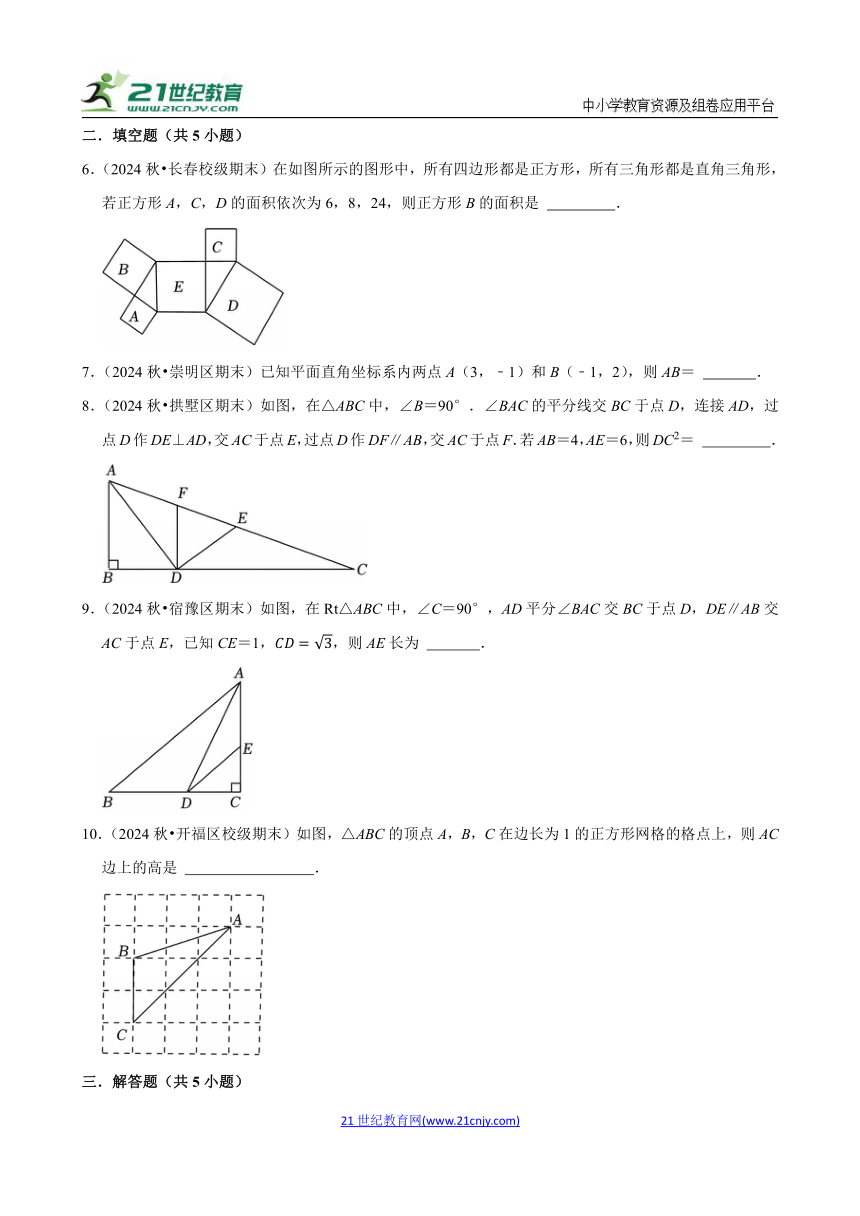
6.(2024秋 长春校级期末)在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为6,8,24,则正方形B的面积是 .
7.(2024秋 崇明区期末)已知平面直角坐标系内两点A(3,﹣1)和B(﹣1,2),则AB= .
8.(2024秋 拱墅区期末)如图,在△ABC中,∠B=90°.∠BAC的平分线交BC于点D,连接AD,过点D作DE⊥AD,交AC于点E,过点D作DF∥AB,交AC于点F.若AB=4,AE=6,则DC2= .
9.(2024秋 宿豫区期末)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,已知CE=1,,则AE长为 .
10.(2024秋 开福区校级期末)如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,则AC边上的高是 .
三.解答题(共5小题)
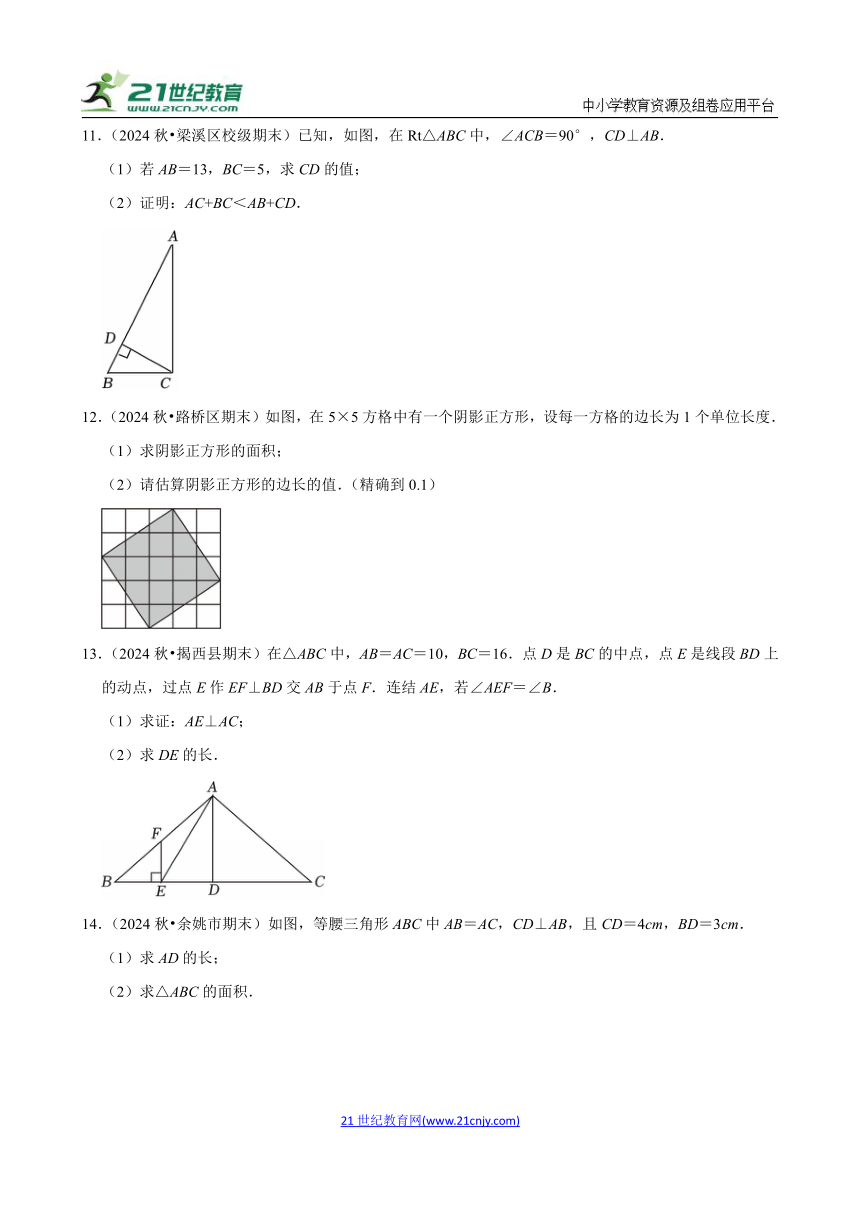
11.(2024秋 梁溪区校级期末)已知,如图,在Rt△ABC中,∠ACB=90°,CD⊥AB.
(1)若AB=13,BC=5,求CD的值;
(2)证明:AC+BC<AB+CD.
12.(2024秋 路桥区期末)如图,在5×5方格中有一个阴影正方形,设每一方格的边长为1个单位长度.
(1)求阴影正方形的面积;
(2)请估算阴影正方形的边长的值.(精确到0.1)
13.(2024秋 揭西县期末)在△ABC中,AB=AC=10,BC=16.点D是BC的中点,点E是线段BD上的动点,过点E作EF⊥BD交AB于点F.连结AE,若∠AEF=∠B.
(1)求证:AE⊥AC;
(2)求DE的长.
14.(2024秋 余姚市期末)如图,等腰三角形ABC中AB=AC,CD⊥AB,且CD=4cm,BD=3cm.
(1)求AD的长;
(2)求△ABC的面积.
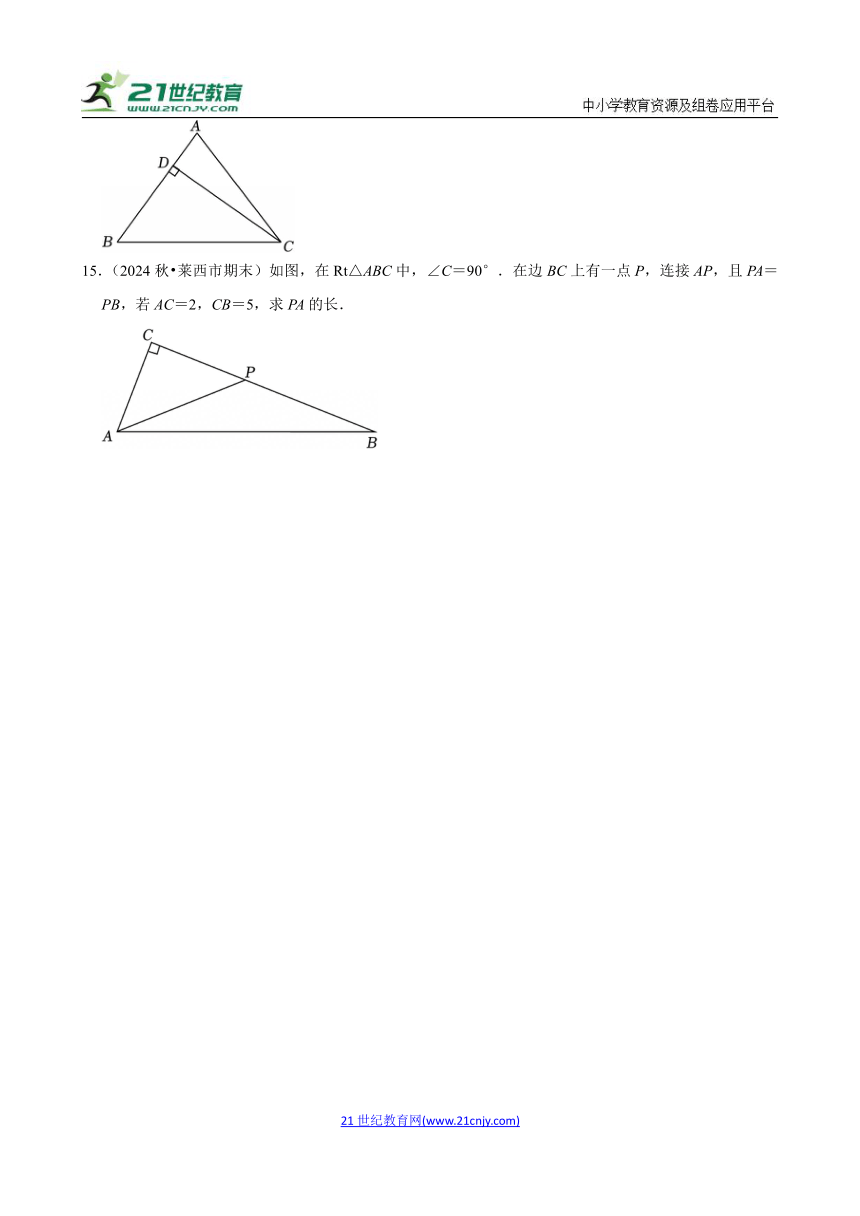
15.(2024秋 莱西市期末)如图,在Rt△ABC中,∠C=90°.在边BC上有一点P,连接AP,且PA=PB,若AC=2,CB=5,求PA的长.
期末专项培优 勾股定理
参考答案与试题解析
题号 1 2 3 4 5
答案 B C C A D
一.选择题(共5小题)
1.(2024秋 长春校级期末)如图,数轴上点A,B对应的数分别是1,2,以AB为边在数轴上方作正方形ABCD,连接AC,以A为圆心,AC的长为半径画圆弧交数轴于点E(点E在点A的左侧),则点E在数轴上对应的数为( )
A. B. C. D.
【考点】勾股定理;实数与数轴.
【专题】实数;等腰三角形与直角三角形;运算能力.
【答案】B
【分析】首先利用勾股定理计算出AC的长,进而可得AE的长,然后再确定E点所对应的数.
【解答】解:∵点A,B对应在数分别是1,2,
∴AB=1,
∵四边形ABCD是正方形,
∴CB=AB=1,
∴AC,
∴AE,
∵点A对应的数是1,
∴E在数轴上对应在数为,
故选:B.
【点评】本题考查了实数与数轴,勾股定理,熟练掌握勾股定理是解题的关键.
2.(2024秋 拱墅区期末)一个直角三角形,若三边的平方和为200,则斜边长为( )
A.8 B.9 C.10 D.11
【考点】勾股定理.
【专题】等腰三角形与直角三角形;运算能力.
【答案】C
【分析】设直角三角形的三边长为 a、b、c,c 为斜边,则由勾股定理得:a2+b2=c2即可求解.
【解答】解:设直角三角形的三边长为 a、b、c,c 为斜边,则由勾股定理得:a2+b2=c2.
∵一个直角三角形的三边长的平方和为200,
∴a2+b2+c2=200,
∴2c2=200,
∴c2=100,
∴c =10,即斜边长为10.
故选:C.
【点评】本题考查勾股定理,正确进行计算是解题关键.
3.(2024秋 源城区期末)已知一个直角三角形的两条边长分别为和1,则第三边长为( )
A. B.2 C.或2 D.或4
【考点】勾股定理.
【专题】分类讨论;等腰三角形与直角三角形;运算能力.
【答案】C
【分析】分两种情况,①当和1均为直角边时,②当1为直角边,为斜边时,根据勾股定理分别求出第三条边长即可.
【解答】解:分两种情况:
①当和1均为直角边时,第三条边长2;
②当1为直角边,为斜边时,第三条边长;
综上所述,第三边长为或2,
故选:C.
【点评】本题主要考查了勾股定理,熟练掌握勾股定理,进行分类讨论是解题的关键.
4.(2024秋 建邺区期末)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以各边为直径作半圆,则图中阴影部分的面积为( )
A.6 B. C.4π﹣6 D.
【考点】勾股定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;运算能力;推理能力.
【答案】A
【分析】先根据勾股定理求出AB,然后根据S阴影=S半圆AC+S半圆BC+S△ABC﹣S半圆AB计算即可.
【解答】解:由勾股定理得,AB2=AC2+BC2=25,
则阴影部分的面积AC×BCπ×()2π×()2π×()2
3×4π(AC2+BC2﹣AB2)
=6,
故选:A.
【点评】本题考查的是勾股定理、扇形面积计算,掌握勾股定理和扇形面积公式是解题的关键.
5.(2024秋 滨湖区期末)“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m,n(m>n).若小正方形面积为7,(m+n)2=21,则大正方形面积为( )
A.11 B.12 C.13 D.14
【考点】勾股定理的证明.
【专题】三角形;推理能力.
【答案】D
【分析】根据小正方形面积为7得出(m﹣n)2=7,结合(m+n)2=21,得出2mn的值,即可得出结果.
【解答】解:∵小正方形面积为7,
∴(m﹣n)2=7,
又∵(m+n)2=21,
∴(m+n)2﹣(m﹣n)2=14,
∴2mn=7.
又∵大正方形的面积4+(m﹣n)2=m2+n2,
∴m2+n2=(m+n)2﹣2mn=21﹣7=14,
故选:D.
【点评】本题考查了勾股定理的证明,正确表示出2nm的值是解题的关键.
二.填空题(共5小题)
6.(2024秋 长春校级期末)在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为6,8,24,则正方形B的面积是 10 .
【考点】勾股定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】10.
【分析】根据勾股定理得到SA+SB=SE,SD﹣SC=SE,进一步运算即可.
【解答】解:由图可知,SA+SB=SE,SD﹣SC=SE,
∴S正方形A+S正方形B=S正方形D﹣S正方形C,正方形A,C,D的面积依次为6,8,24,
∴正方形B的面积+6=24﹣8,
∴正方形B的面积=10.
故答案为:10
【点评】本题考查了勾股定理,要熟悉勾股定理的几何意义,知道直角三角形两直角边的平方和等于斜边的平方.
7.(2024秋 崇明区期末)已知平面直角坐标系内两点A(3,﹣1)和B(﹣1,2),则AB= 5 .
【考点】勾股定理;两点间的距离公式.
【专题】平面直角坐标系;等腰三角形与直角三角形;推理能力.
【答案】5.
【分析】利用两点间的距离公式计算即可.
【解答】解:根据两点间的距离公式可知:AB5,
故答案为:5.
【点评】此题主要考查了勾股定理,两点之间的距离公式,掌握两点之间的距离公式是解题的关键.
8.(2024秋 拱墅区期末)如图,在△ABC中,∠B=90°.∠BAC的平分线交BC于点D,连接AD,过点D作DE⊥AD,交AC于点E,过点D作DF∥AB,交AC于点F.若AB=4,AE=6,则DC2= 72 .
【考点】勾股定理;等腰三角形的判定与性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】72.
【分析】(1)过D作DG⊥AC于G,可证△ABD≌△AGD(HL),AB=AG=4,EG=2,再通过△ADG∽△DGE,可得BD=DG=2,再根据△ABC∽△DGC可得ACDC,再利用勾股定理求解即可.
【解答】解:过D作DG⊥AC于G,
∵∠BAC的平分线交BC于点D,
∴∠1=∠2,DB=DG,
又∵AD=AD,
∴△ABD≌△AGD(HL),
∴AB=AG=4,
∴EG=AE﹣AG=2,
∵DG⊥ACN,
∴∠2+∠ADG=90°,
∴△ADG∽△DGE,
∴,即,
∴DG=2,BD=DG=2,
∵∠ABC=∠DGC=90°,∠C=∠C,
∴△ABC∽△DGC,
∴,即,
∴ACDC,
∴42,
解得DC=6或﹣2(舍去),
∴DC2=72.
故答案为:72.
【点评】本题考查勾股定理,正确进行计算是解题关键.
9.(2024秋 宿豫区期末)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,已知CE=1,,则AE长为 2 .
【考点】勾股定理;角平分线的性质;等腰三角形的判定与性质.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;运算能力;推理能力.
【答案】2.
【分析】由勾股定理求出DE=2,再由角平分线的定义和平行线的性质证明∠ADE=∠EAD,然后由等腰三角形的判定得出AE=DE=2即可.
【解答】解:在Rt△CDE中,∠C=90°,CE=1,,
由勾股定理得:DE2,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠ADE=∠EAD,
∴AE=DE=2,
故答案为:2.
【点评】本题主要考查了勾股定理、等腰三角形的判定、平行线的性质以及角平分线的定义等知识,熟练掌握勾股定理,证明AE=DE是解题的关键.
10.(2024秋 开福区校级期末)如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,则AC边上的高是 .
【考点】勾股定理.
【专题】网格型;等腰三角形与直角三角形.
【答案】.
【分析】取格点D,连接BD交AC于格点E,则BE即为AC边上的高,再根据勾股定理求解即可.
【解答】解:如图,取格点D,连接BD交AC于格点E,则BE即为AC边上的高,
∴BE,
故答案为:.
【点评】本题考查了勾股定理,正方形的性质,正确作出AC边上的高是解题的关键.
三.解答题(共5小题)
11.(2024秋 梁溪区校级期末)已知,如图,在Rt△ABC中,∠ACB=90°,CD⊥AB.
(1)若AB=13,BC=5,求CD的值;
(2)证明:AC+BC<AB+CD.
【考点】勾股定理;三角形三边关系.
【专题】三角形;运算能力;推理能力.
【答案】(1);
(2)证明见解析过程.
【分析】(1)利用勾股定理及面积法即可解决问题.
(2)将不等式两边的式子分别平方,再结合勾股定理及面积法即可进行证明.
【解答】(1)解:∵∠ACB=90°,AB=13,BC=5,
∴AC12,
∵CD⊥AB,
∴S△ABC,
∴CD;
(2)证明:∵(AC+BC)2=AC2+BC2+2AC BC,(AB+CD)2=AB2+CD2+2AB CD,且AC2+BC2=AB2,
∴(AC+BC)2﹣(AB+CD)2=(AB2+2AC BC)﹣(AB2+CD2+2AB CD)=2AC BC﹣CD2﹣2AB CD.
又∵,
∴2AC BC﹣CD2﹣2AB CD=﹣CD2<0,
∴(AC+BC)2<(AB+CD)2,
∴AC+BC<AB+CD.
【点评】本题主要考查了勾股定理及三角形三边的关系,熟知勾股定理及三角形三边的关系是解题的关键.
12.(2024秋 路桥区期末)如图,在5×5方格中有一个阴影正方形,设每一方格的边长为1个单位长度.
(1)求阴影正方形的面积;
(2)请估算阴影正方形的边长的值.(精确到0.1)
【考点】勾股定理;近似数和有效数字.
【专题】实数;等腰三角形与直角三角形;运算能力.
【答案】(1)13;
(2)3.6.
【分析】(1)由勾股定理求出阴影正方形的边长,即可解决问题;
(2)根据近似数的要求进行估算即可.
【解答】解:(1)由勾股定理得:阴影正方形的边长,
∴阴影正方形的面积=()2=13;
(2)由(1)可知,阴影正方形的边长3.6.
【点评】本题主要考查了勾股定理以及近似数,熟练掌握勾股定理是解题的关键.
13.(2024秋 揭西县期末)在△ABC中,AB=AC=10,BC=16.点D是BC的中点,点E是线段BD上的动点,过点E作EF⊥BD交AB于点F.连结AE,若∠AEF=∠B.
(1)求证:AE⊥AC;
(2)求DE的长.
【考点】勾股定理;等腰三角形的性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】见试题解答内容
【分析】(1)根据等腰三角形的性质得到∠B=∠C,证明∠EAC=90°,根据垂直的定义即可得证;
(2)根据勾股定理计算,得到答案.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵EF⊥BD,
∴∠AEF+∠AED=90°,
∵∠AEF=∠B,∠B=∠C,
∴∠C+∠AED=90°,
∴∠EAC=90°,
∴AE⊥AC;
(2)解:∵∠EAC=90°,
∴AE2+AC2=CE2,
∵CE=CD+DE=DE+8,
∴AE2=CE2﹣AC2=(DE+8)2﹣102,
∵AB=AC,点D是BC的中点,
∴BD=DC16=8,BC=16,AD⊥BC,
∴AD6,
在Rt△ADE中,AE2=AD2+DE2=62+DE2,
∴(DE+8)2﹣102=62+DE2,
解得:DE=4.5.
【点评】本题考查的是勾股定理、等腰三角形的性质,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
14.(2024秋 余姚市期末)如图,等腰三角形ABC中AB=AC,CD⊥AB,且CD=4cm,BD=3cm.
(1)求AD的长;
(2)求△ABC的面积.
【考点】勾股定理;等腰三角形的性质.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】(1)cm;
(2)cm2.
【分析】(1)设AD=x cm,AB=AC=(x+3)cm,在Rt△ADC中,由勾股定理列出方程,解方程即可;
(2)根据三角形的面积公式列式计算即可.
【解答】解:(1)设AD=x cm,则AB=AC=(x+3)cm,
∵CD⊥AB,
∴∠CDA=90°,
在Rt△ACD中,根据题意得:x2+42=(x+3)2,
解得:x,
答:AD的长为cm;
(2)由(1)可知,AB=AC3(cm),
∵CD⊥AB,
∴S△ABCAB CD4(cm2),
答:△ABC的面积为cm2.
【点评】此题考查的是勾股定理、等腰三角形的性质以及三角形面积等知识,根据勾股定理列出方程是解题的关键.
15.(2024秋 莱西市期末)如图,在Rt△ABC中,∠C=90°.在边BC上有一点P,连接AP,且PA=PB,若AC=2,CB=5,求PA的长.
【考点】勾股定理.
【专题】等腰三角形与直角三角形;运算能力.
【答案】见试题解答内容
【分析】设PA=x=PB,则CP=5﹣x,在Rt△APC中,利用勾股定理列式计算即可求解.
【解答】解:设PA=x=PB,可得:CP=5﹣x,
∵根据勾股定理可得:AC2+CP2=PA2,
∴22+(5﹣x)2=x2,
,
∴PA的长为.
【点评】本题主要考查了勾股定理,正确进行计算是解题关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 长春校级期末)如图,数轴上点A,B对应的数分别是1,2,以AB为边在数轴上方作正方形ABCD,连接AC,以A为圆心,AC的长为半径画圆弧交数轴于点E(点E在点A的左侧),则点E在数轴上对应的数为( )
A. B. C. D.
2.(2024秋 拱墅区期末)一个直角三角形,若三边的平方和为200,则斜边长为( )
A.8 B.9 C.10 D.11
3.(2024秋 源城区期末)已知一个直角三角形的两条边长分别为和1,则第三边长为( )
A. B.2 C.或2 D.或4
4.(2024秋 建邺区期末)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以各边为直径作半圆,则图中阴影部分的面积为( )
A.6 B. C.4π﹣6 D.
5.(2024秋 滨湖区期末)“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m,n(m>n).若小正方形面积为7,(m+n)2=21,则大正方形面积为( )
A.11 B.12 C.13 D.14
二.填空题(共5小题)
6.(2024秋 长春校级期末)在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为6,8,24,则正方形B的面积是 .
7.(2024秋 崇明区期末)已知平面直角坐标系内两点A(3,﹣1)和B(﹣1,2),则AB= .
8.(2024秋 拱墅区期末)如图,在△ABC中,∠B=90°.∠BAC的平分线交BC于点D,连接AD,过点D作DE⊥AD,交AC于点E,过点D作DF∥AB,交AC于点F.若AB=4,AE=6,则DC2= .
9.(2024秋 宿豫区期末)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,已知CE=1,,则AE长为 .
10.(2024秋 开福区校级期末)如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,则AC边上的高是 .
三.解答题(共5小题)
11.(2024秋 梁溪区校级期末)已知,如图,在Rt△ABC中,∠ACB=90°,CD⊥AB.
(1)若AB=13,BC=5,求CD的值;
(2)证明:AC+BC<AB+CD.
12.(2024秋 路桥区期末)如图,在5×5方格中有一个阴影正方形,设每一方格的边长为1个单位长度.
(1)求阴影正方形的面积;
(2)请估算阴影正方形的边长的值.(精确到0.1)
13.(2024秋 揭西县期末)在△ABC中,AB=AC=10,BC=16.点D是BC的中点,点E是线段BD上的动点,过点E作EF⊥BD交AB于点F.连结AE,若∠AEF=∠B.
(1)求证:AE⊥AC;
(2)求DE的长.
14.(2024秋 余姚市期末)如图,等腰三角形ABC中AB=AC,CD⊥AB,且CD=4cm,BD=3cm.
(1)求AD的长;
(2)求△ABC的面积.
15.(2024秋 莱西市期末)如图,在Rt△ABC中,∠C=90°.在边BC上有一点P,连接AP,且PA=PB,若AC=2,CB=5,求PA的长.
期末专项培优 勾股定理
参考答案与试题解析
题号 1 2 3 4 5
答案 B C C A D
一.选择题(共5小题)
1.(2024秋 长春校级期末)如图,数轴上点A,B对应的数分别是1,2,以AB为边在数轴上方作正方形ABCD,连接AC,以A为圆心,AC的长为半径画圆弧交数轴于点E(点E在点A的左侧),则点E在数轴上对应的数为( )
A. B. C. D.
【考点】勾股定理;实数与数轴.
【专题】实数;等腰三角形与直角三角形;运算能力.
【答案】B
【分析】首先利用勾股定理计算出AC的长,进而可得AE的长,然后再确定E点所对应的数.
【解答】解:∵点A,B对应在数分别是1,2,
∴AB=1,
∵四边形ABCD是正方形,
∴CB=AB=1,
∴AC,
∴AE,
∵点A对应的数是1,
∴E在数轴上对应在数为,
故选:B.
【点评】本题考查了实数与数轴,勾股定理,熟练掌握勾股定理是解题的关键.
2.(2024秋 拱墅区期末)一个直角三角形,若三边的平方和为200,则斜边长为( )
A.8 B.9 C.10 D.11
【考点】勾股定理.
【专题】等腰三角形与直角三角形;运算能力.
【答案】C
【分析】设直角三角形的三边长为 a、b、c,c 为斜边,则由勾股定理得:a2+b2=c2即可求解.
【解答】解:设直角三角形的三边长为 a、b、c,c 为斜边,则由勾股定理得:a2+b2=c2.
∵一个直角三角形的三边长的平方和为200,
∴a2+b2+c2=200,
∴2c2=200,
∴c2=100,
∴c =10,即斜边长为10.
故选:C.
【点评】本题考查勾股定理,正确进行计算是解题关键.
3.(2024秋 源城区期末)已知一个直角三角形的两条边长分别为和1,则第三边长为( )
A. B.2 C.或2 D.或4
【考点】勾股定理.
【专题】分类讨论;等腰三角形与直角三角形;运算能力.
【答案】C
【分析】分两种情况,①当和1均为直角边时,②当1为直角边,为斜边时,根据勾股定理分别求出第三条边长即可.
【解答】解:分两种情况:
①当和1均为直角边时,第三条边长2;
②当1为直角边,为斜边时,第三条边长;
综上所述,第三边长为或2,
故选:C.
【点评】本题主要考查了勾股定理,熟练掌握勾股定理,进行分类讨论是解题的关键.
4.(2024秋 建邺区期末)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以各边为直径作半圆,则图中阴影部分的面积为( )
A.6 B. C.4π﹣6 D.
【考点】勾股定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;运算能力;推理能力.
【答案】A
【分析】先根据勾股定理求出AB,然后根据S阴影=S半圆AC+S半圆BC+S△ABC﹣S半圆AB计算即可.
【解答】解:由勾股定理得,AB2=AC2+BC2=25,
则阴影部分的面积AC×BCπ×()2π×()2π×()2
3×4π(AC2+BC2﹣AB2)
=6,
故选:A.
【点评】本题考查的是勾股定理、扇形面积计算,掌握勾股定理和扇形面积公式是解题的关键.
5.(2024秋 滨湖区期末)“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m,n(m>n).若小正方形面积为7,(m+n)2=21,则大正方形面积为( )
A.11 B.12 C.13 D.14
【考点】勾股定理的证明.
【专题】三角形;推理能力.
【答案】D
【分析】根据小正方形面积为7得出(m﹣n)2=7,结合(m+n)2=21,得出2mn的值,即可得出结果.
【解答】解:∵小正方形面积为7,
∴(m﹣n)2=7,
又∵(m+n)2=21,
∴(m+n)2﹣(m﹣n)2=14,
∴2mn=7.
又∵大正方形的面积4+(m﹣n)2=m2+n2,
∴m2+n2=(m+n)2﹣2mn=21﹣7=14,
故选:D.
【点评】本题考查了勾股定理的证明,正确表示出2nm的值是解题的关键.
二.填空题(共5小题)
6.(2024秋 长春校级期末)在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为6,8,24,则正方形B的面积是 10 .
【考点】勾股定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】10.
【分析】根据勾股定理得到SA+SB=SE,SD﹣SC=SE,进一步运算即可.
【解答】解:由图可知,SA+SB=SE,SD﹣SC=SE,
∴S正方形A+S正方形B=S正方形D﹣S正方形C,正方形A,C,D的面积依次为6,8,24,
∴正方形B的面积+6=24﹣8,
∴正方形B的面积=10.
故答案为:10
【点评】本题考查了勾股定理,要熟悉勾股定理的几何意义,知道直角三角形两直角边的平方和等于斜边的平方.
7.(2024秋 崇明区期末)已知平面直角坐标系内两点A(3,﹣1)和B(﹣1,2),则AB= 5 .
【考点】勾股定理;两点间的距离公式.
【专题】平面直角坐标系;等腰三角形与直角三角形;推理能力.
【答案】5.
【分析】利用两点间的距离公式计算即可.
【解答】解:根据两点间的距离公式可知:AB5,
故答案为:5.
【点评】此题主要考查了勾股定理,两点之间的距离公式,掌握两点之间的距离公式是解题的关键.
8.(2024秋 拱墅区期末)如图,在△ABC中,∠B=90°.∠BAC的平分线交BC于点D,连接AD,过点D作DE⊥AD,交AC于点E,过点D作DF∥AB,交AC于点F.若AB=4,AE=6,则DC2= 72 .
【考点】勾股定理;等腰三角形的判定与性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】72.
【分析】(1)过D作DG⊥AC于G,可证△ABD≌△AGD(HL),AB=AG=4,EG=2,再通过△ADG∽△DGE,可得BD=DG=2,再根据△ABC∽△DGC可得ACDC,再利用勾股定理求解即可.
【解答】解:过D作DG⊥AC于G,
∵∠BAC的平分线交BC于点D,
∴∠1=∠2,DB=DG,
又∵AD=AD,
∴△ABD≌△AGD(HL),
∴AB=AG=4,
∴EG=AE﹣AG=2,
∵DG⊥ACN,
∴∠2+∠ADG=90°,
∴△ADG∽△DGE,
∴,即,
∴DG=2,BD=DG=2,
∵∠ABC=∠DGC=90°,∠C=∠C,
∴△ABC∽△DGC,
∴,即,
∴ACDC,
∴42,
解得DC=6或﹣2(舍去),
∴DC2=72.
故答案为:72.
【点评】本题考查勾股定理,正确进行计算是解题关键.
9.(2024秋 宿豫区期末)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,已知CE=1,,则AE长为 2 .
【考点】勾股定理;角平分线的性质;等腰三角形的判定与性质.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;运算能力;推理能力.
【答案】2.
【分析】由勾股定理求出DE=2,再由角平分线的定义和平行线的性质证明∠ADE=∠EAD,然后由等腰三角形的判定得出AE=DE=2即可.
【解答】解:在Rt△CDE中,∠C=90°,CE=1,,
由勾股定理得:DE2,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠ADE=∠EAD,
∴AE=DE=2,
故答案为:2.
【点评】本题主要考查了勾股定理、等腰三角形的判定、平行线的性质以及角平分线的定义等知识,熟练掌握勾股定理,证明AE=DE是解题的关键.
10.(2024秋 开福区校级期末)如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,则AC边上的高是 .
【考点】勾股定理.
【专题】网格型;等腰三角形与直角三角形.
【答案】.
【分析】取格点D,连接BD交AC于格点E,则BE即为AC边上的高,再根据勾股定理求解即可.
【解答】解:如图,取格点D,连接BD交AC于格点E,则BE即为AC边上的高,
∴BE,
故答案为:.
【点评】本题考查了勾股定理,正方形的性质,正确作出AC边上的高是解题的关键.
三.解答题(共5小题)
11.(2024秋 梁溪区校级期末)已知,如图,在Rt△ABC中,∠ACB=90°,CD⊥AB.
(1)若AB=13,BC=5,求CD的值;
(2)证明:AC+BC<AB+CD.
【考点】勾股定理;三角形三边关系.
【专题】三角形;运算能力;推理能力.
【答案】(1);
(2)证明见解析过程.
【分析】(1)利用勾股定理及面积法即可解决问题.
(2)将不等式两边的式子分别平方,再结合勾股定理及面积法即可进行证明.
【解答】(1)解:∵∠ACB=90°,AB=13,BC=5,
∴AC12,
∵CD⊥AB,
∴S△ABC,
∴CD;
(2)证明:∵(AC+BC)2=AC2+BC2+2AC BC,(AB+CD)2=AB2+CD2+2AB CD,且AC2+BC2=AB2,
∴(AC+BC)2﹣(AB+CD)2=(AB2+2AC BC)﹣(AB2+CD2+2AB CD)=2AC BC﹣CD2﹣2AB CD.
又∵,
∴2AC BC﹣CD2﹣2AB CD=﹣CD2<0,
∴(AC+BC)2<(AB+CD)2,
∴AC+BC<AB+CD.
【点评】本题主要考查了勾股定理及三角形三边的关系,熟知勾股定理及三角形三边的关系是解题的关键.
12.(2024秋 路桥区期末)如图,在5×5方格中有一个阴影正方形,设每一方格的边长为1个单位长度.
(1)求阴影正方形的面积;
(2)请估算阴影正方形的边长的值.(精确到0.1)
【考点】勾股定理;近似数和有效数字.
【专题】实数;等腰三角形与直角三角形;运算能力.
【答案】(1)13;
(2)3.6.
【分析】(1)由勾股定理求出阴影正方形的边长,即可解决问题;
(2)根据近似数的要求进行估算即可.
【解答】解:(1)由勾股定理得:阴影正方形的边长,
∴阴影正方形的面积=()2=13;
(2)由(1)可知,阴影正方形的边长3.6.
【点评】本题主要考查了勾股定理以及近似数,熟练掌握勾股定理是解题的关键.
13.(2024秋 揭西县期末)在△ABC中,AB=AC=10,BC=16.点D是BC的中点,点E是线段BD上的动点,过点E作EF⊥BD交AB于点F.连结AE,若∠AEF=∠B.
(1)求证:AE⊥AC;
(2)求DE的长.
【考点】勾股定理;等腰三角形的性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】见试题解答内容
【分析】(1)根据等腰三角形的性质得到∠B=∠C,证明∠EAC=90°,根据垂直的定义即可得证;
(2)根据勾股定理计算,得到答案.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵EF⊥BD,
∴∠AEF+∠AED=90°,
∵∠AEF=∠B,∠B=∠C,
∴∠C+∠AED=90°,
∴∠EAC=90°,
∴AE⊥AC;
(2)解:∵∠EAC=90°,
∴AE2+AC2=CE2,
∵CE=CD+DE=DE+8,
∴AE2=CE2﹣AC2=(DE+8)2﹣102,
∵AB=AC,点D是BC的中点,
∴BD=DC16=8,BC=16,AD⊥BC,
∴AD6,
在Rt△ADE中,AE2=AD2+DE2=62+DE2,
∴(DE+8)2﹣102=62+DE2,
解得:DE=4.5.
【点评】本题考查的是勾股定理、等腰三角形的性质,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
14.(2024秋 余姚市期末)如图,等腰三角形ABC中AB=AC,CD⊥AB,且CD=4cm,BD=3cm.
(1)求AD的长;
(2)求△ABC的面积.
【考点】勾股定理;等腰三角形的性质.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】(1)cm;
(2)cm2.
【分析】(1)设AD=x cm,AB=AC=(x+3)cm,在Rt△ADC中,由勾股定理列出方程,解方程即可;
(2)根据三角形的面积公式列式计算即可.
【解答】解:(1)设AD=x cm,则AB=AC=(x+3)cm,
∵CD⊥AB,
∴∠CDA=90°,
在Rt△ACD中,根据题意得:x2+42=(x+3)2,
解得:x,
答:AD的长为cm;
(2)由(1)可知,AB=AC3(cm),
∵CD⊥AB,
∴S△ABCAB CD4(cm2),
答:△ABC的面积为cm2.
【点评】此题考查的是勾股定理、等腰三角形的性质以及三角形面积等知识,根据勾股定理列出方程是解题的关键.
15.(2024秋 莱西市期末)如图,在Rt△ABC中,∠C=90°.在边BC上有一点P,连接AP,且PA=PB,若AC=2,CB=5,求PA的长.
【考点】勾股定理.
【专题】等腰三角形与直角三角形;运算能力.
【答案】见试题解答内容
【分析】设PA=x=PB,则CP=5﹣x,在Rt△APC中,利用勾股定理列式计算即可求解.
【解答】解:设PA=x=PB,可得:CP=5﹣x,
∵根据勾股定理可得:AC2+CP2=PA2,
∴22+(5﹣x)2=x2,
,
∴PA的长为.
【点评】本题主要考查了勾股定理,正确进行计算是解题关键.
21世纪教育网(www.21cnjy.com)
