【期末专项培优】函数(含解析)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 【期末专项培优】函数(含解析)2024-2025学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 00:00:00 | ||
图片预览


文档简介
期末专项培优 函数
一.选择题(共5小题)
1.(2024秋 南岸区期末)下面属于定量数据的是( )
A.汽车的产量 B.购买商品的支付方式
C.性别 D.学历
2.(2024秋 南海区期末)你知道为什么冬天电瓶车电池不耐用?因为电瓶车通常使用铅酸电池和锂电池,这两种电池的最佳使用温度都是25摄氏度左右.随着温度降低,电池中的化学物质活性降低,从而导致电池不耐用.在这个变化过程中,自变量是( )
A.化学物质 B.温度 C.电池 D.电瓶车
3.(2025 潍坊模拟)某年部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,中国创新综合排名全球第22名,创新效率排名位于全球( )
A.第4名 B.第3名 C.第2名 D.第1名
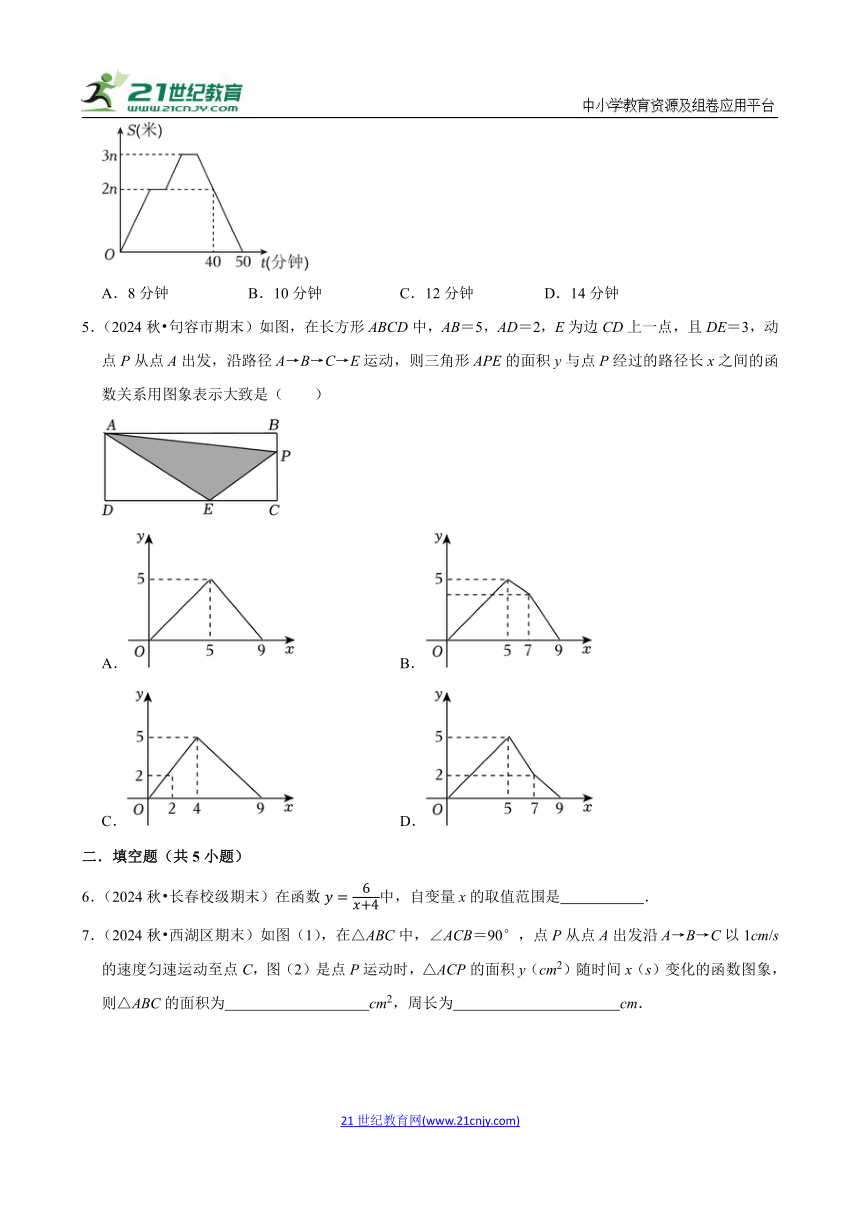
4.(2024秋 浦江县期末)【情境】跑步是一种简单而强大的有氧运动,被广泛认为是最佳的锻炼方式.周末小明从家出发跑步去健身主题公园,中途休息一段时间,到达健身公园后又再次休息,之后跑步返回家中,已知小明两次休息时间相同且跑步速度始终不变.小明离开家的路程S与时间t的关系(部分数据)如图所示.
【问题】小明每次休息的时间为( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
5.(2024秋 句容市期末)如图,在长方形ABCD中,AB=5,AD=2,E为边CD上一点,且DE=3,动点P从点A出发,沿路径A→B→C→E运动,则三角形APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )
A. B.
C. D.
二.填空题(共5小题)
6.(2024秋 长春校级期末)在函数中,自变量x的取值范围是 .
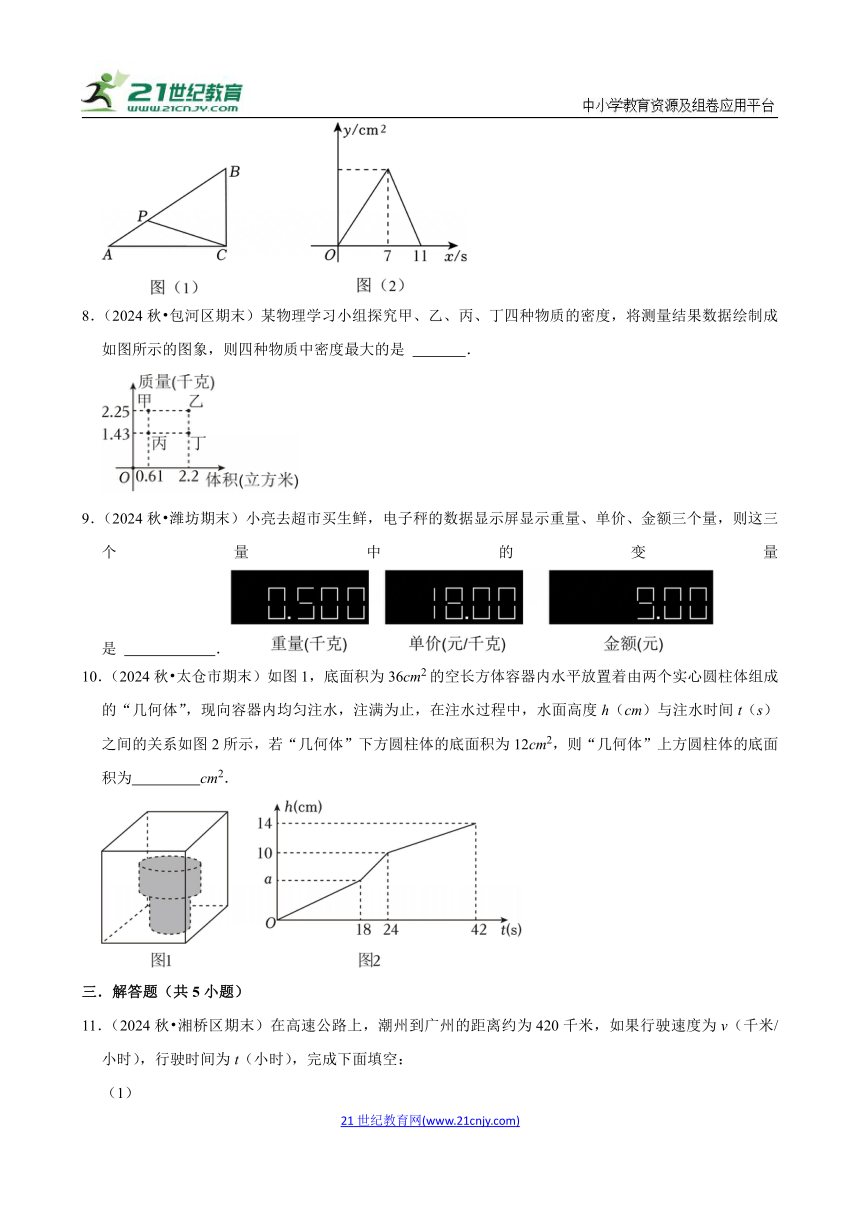
7.(2024秋 西湖区期末)如图(1),在△ABC中,∠ACB=90°,点P从点A出发沿A→B→C以1cm/s的速度匀速运动至点C,图(2)是点P运动时,△ACP的面积y(cm2)随时间x(s)变化的函数图象,则△ABC的面积为 cm2,周长为 cm.
8.(2024秋 包河区期末)某物理学习小组探究甲、乙、丙、丁四种物质的密度,将测量结果数据绘制成如图所示的图象,则四种物质中密度最大的是 .
9.(2024秋 潍坊期末)小亮去超市买生鲜,电子秤的数据显示屏显示重量、单价、金额三个量,则这三个量中的变量是 .
10.(2024秋 太仓市期末)如图1,底面积为36cm2的空长方体容器内水平放置着由两个实心圆柱体组成的“几何体”,现向容器内均匀注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图2所示,若“几何体”下方圆柱体的底面积为12cm2,则“几何体”上方圆柱体的底面积为 cm2.
三.解答题(共5小题)
11.(2024秋 湘桥区期末)在高速公路上,潮州到广州的距离约为420千米,如果行驶速度为v(千米/小时),行驶时间为t(小时),完成下面填空:
(1)
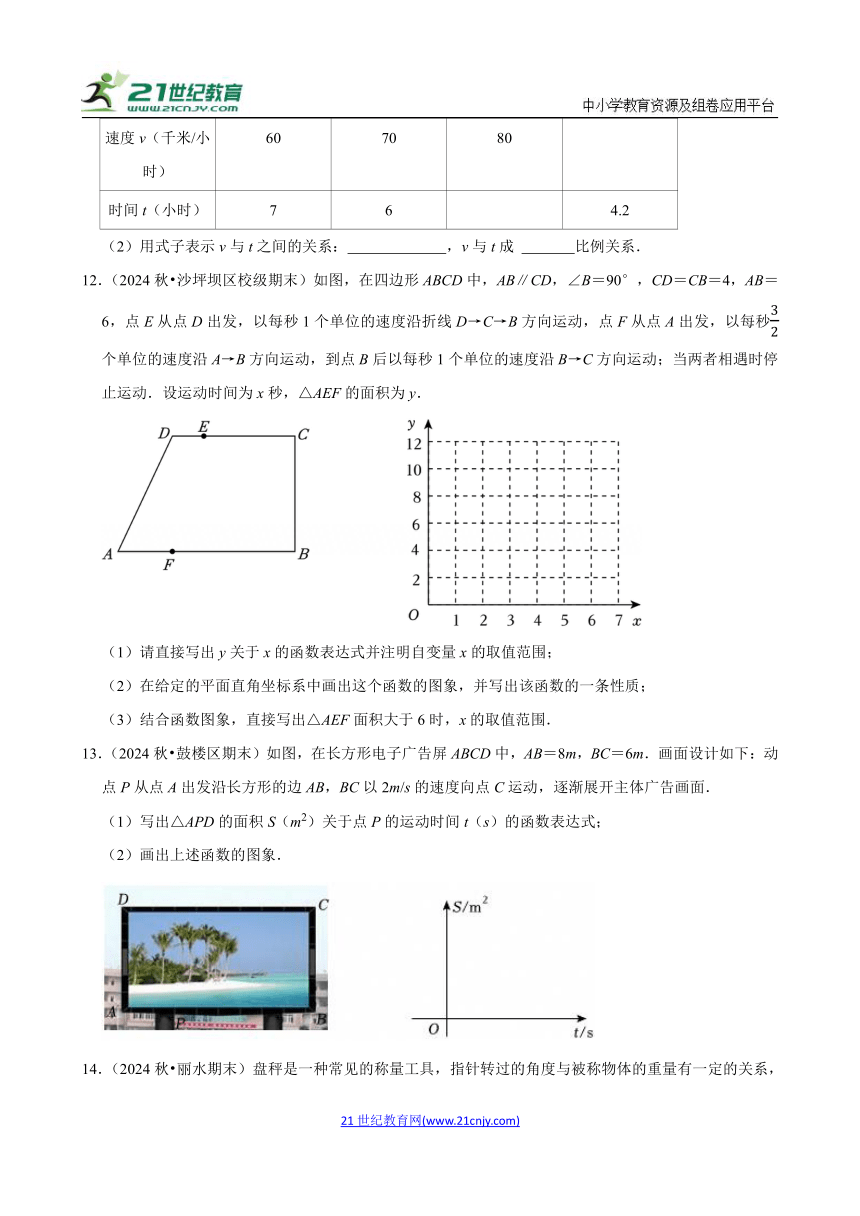
速度v(千米/小时) 60 70 80
时间t(小时) 7 6 4.2
(2)用式子表示v与t之间的关系: ,v与t成 比例关系.
12.(2024秋 沙坪坝区校级期末)如图,在四边形ABCD中,AB∥CD,∠B=90°,CD=CB=4,AB=6,点E从点D出发,以每秒1个单位的速度沿折线D→C→B方向运动,点F从点A出发,以每秒个单位的速度沿A→B方向运动,到点B后以每秒1个单位的速度沿B→C方向运动;当两者相遇时停止运动.设运动时间为x秒,△AEF的面积为y.
(1)请直接写出y关于x的函数表达式并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出△AEF面积大于6时,x的取值范围.
13.(2024秋 鼓楼区期末)如图,在长方形电子广告屏ABCD中,AB=8m,BC=6m.画面设计如下:动点P从点A出发沿长方形的边AB,BC以2m/s的速度向点C运动,逐渐展开主体广告画面.
(1)写出△APD的面积S(m2)关于点P的运动时间t(s)的函数表达式;
(2)画出上述函数的图象.
14.(2024秋 丽水期末)盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如表所示:
重量(单位:千克) 0 2 2.5 3 b
指针转过的角度 0° 36° a° 54° 180°
(1)请直接写出a、b的值;
(2)指针转过的角度不得超过360°,否则盘秤会受损,称量18千克的物品会对盘秤造成损伤吗?说说你的理由.
(3)某顾客在一家水果店购买水果,用这种盘秤称量两次,第二次的数量是第一次数量的2倍多3千克,且指针第二次转过的角度比第一次大108°,该顾客一共购买了多少千克水果.
15.(2024秋 浦东新区校级期末)某校科技节启用无人机航拍活动,在操控无人机时可调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 ;
(2)无人机在75米高的上空停留的时间是 分钟;
(3)在上升或下降过程中,无人机的速度为 米/分;
(4)图中a表示的数是 ;b表示的数是 ;
(5)图中点A表示的实际意义是 .
期末专项培优 函数
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 南岸区期末)下面属于定量数据的是( )
A.汽车的产量 B.购买商品的支付方式
C.性别 D.学历
【考点】常量与变量.
【专题】数与式;应用意识.
【答案】A
【分析】定性数据:也称为分类数据,是非数值型的数据,描述事物的特征或属性.通常以文字、符号或类别来表示,不具备数值意义;定量数据:也称为连续数据或数值型数据,是数值型的数据,可以进行数值计算和统计分析,据此进行判断即可.
【解答】解:定性数据:也称为分类数据,是非数值型的数据,定量数据:也称为连续数据或数值型数据,是数值型的数据,由此可得:
A、汽车的产量,为定量数据,符合题意;
B、购买商品的支付方式,为定性数据,不符合题意;
C、性别,为定性数据,不符合题意;
D、学历,为定性数据,不符合题意.
故选:A.
【点评】本题考查定量数据和定性数据,正确记忆相关定义是解题关键.
2.(2024秋 南海区期末)你知道为什么冬天电瓶车电池不耐用?因为电瓶车通常使用铅酸电池和锂电池,这两种电池的最佳使用温度都是25摄氏度左右.随着温度降低,电池中的化学物质活性降低,从而导致电池不耐用.在这个变化过程中,自变量是( )
A.化学物质 B.温度 C.电池 D.电瓶车
【考点】常量与变量.
【专题】函数及其图象;数感.
【答案】B
【分析】在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量,据此进行判断即可.
【解答】解:随着温度降低,电池中的化学物质活性降低,从而导致电池不耐用.在这个变化过程中,自变量是温度,
故选:B.
【点评】本题考查常量与变量,熟练掌握其定义是解题的关键.
3.(2025 潍坊模拟)某年部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,中国创新综合排名全球第22名,创新效率排名位于全球( )
A.第4名 B.第3名 C.第2名 D.第1名
【考点】函数的图象.
【专题】函数及其图象;几何直观.
【答案】B
【分析】根据中国创新综合排名全球第22名,在坐标系中找到对应的中国创新产出排名为第11名,再根据中国创新产出排名为第11名在另一排名中找到创新效率排名为第3名即可.
【解答】解:如图,
由左图得,中国创新综合排名全球第22名,在坐标系中找到对应的中国创新产出排名为第11名,
由右图得,中国创新产出排名为第11名,创新效率排名为第3名.
故选:B.
【点评】本题考查函数的图象,理解题意是解题的关键.
4.(2024秋 浦江县期末)【情境】跑步是一种简单而强大的有氧运动,被广泛认为是最佳的锻炼方式.周末小明从家出发跑步去健身主题公园,中途休息一段时间,到达健身公园后又再次休息,之后跑步返回家中,已知小明两次休息时间相同且跑步速度始终不变.小明离开家的路程S与时间t的关系(部分数据)如图所示.
【问题】小明每次休息的时间为( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
【考点】函数的图象.
【专题】函数及其图象;运算能力.
【答案】B
【分析】先求出跑步速度,再求出跑步返回家中所用的时间,根据两次休息时间相同且跑步速度始终不变,即可求解.
【解答】解:由题意,小明跑步速度为(米/分钟),
跑步返回家中所用的时间为15(分钟),
∴小明每次休息的时间为(50﹣15×2)=10(分钟),
故选:B.
【点评】本题考查了函数的图象,理解题意,从函数图象中获取有用信息是解题的关键.
5.(2024秋 句容市期末)如图,在长方形ABCD中,AB=5,AD=2,E为边CD上一点,且DE=3,动点P从点A出发,沿路径A→B→C→E运动,则三角形APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )
A. B.
C. D.
【考点】动点问题的函数图象.
【专题】函数及其图象;几何直观;推理能力.
【答案】D
【分析】求出CE的长,然后分三种情况讨论:①点P在AB上运动时,利用三角形的面积公式列式得到y与x的关系式;②点P在BC上运动时,根据S△APE=S梯形ABCE﹣S△ABP﹣S△ECP式整理得到y与x的关系式;③点P在CE上运动时,利用三角形的面积公式列式得到y与x的函数关系,根据解析式即可得到函数的图象.
【解答】解:在长方形ABCD中,AB=5,AD=2,
∴BC=AD=2,CD=AB=5,
∴CE=CD﹣DE=5﹣3=2,
动点P从点A出发,沿路径A→B→C→E运动,当点P在AB上运动,即0≤x≤5时,AP=x,
,
∴y=x(0≤x≤5),
当点P在BC上运动,即5<x≤7时,
BP=x﹣5,CP=5+2﹣x=7﹣x,
∴S△APE=S梯形ABCE﹣S△ABP﹣S△ECP
,
∴(5<x≤7),
当点P在CE上运动,即7<x≤9时,CP=x﹣5﹣2=x﹣7,
EP=EC﹣CP=2﹣(x﹣7)=9﹣x,
∴,
∴y=9﹣x(7<x≤9),
综上所述,函数关系式为,
∴当x=5时,y=5;
当x=7时,y=2;
当x=9时,y=0.
∴选项D的图象符合题意.
故选:D.
【点评】本题考查了动点问题函数图象,读懂题目信息,根据点P的位置的不同分三段列式求出y与x的关系式是解题的关键.
二.填空题(共5小题)
6.(2024秋 长春校级期末)在函数中,自变量x的取值范围是 x≠﹣4 .
【考点】函数自变量的取值范围.
【专题】函数及其图象;运算能力.
【答案】见试题解答内容
【分析】根据分式有意义的条件得出x+4≠0,求解即可.
【解答】解:根据分式有意义的条件可知,x+4≠0,
解得:x≠﹣4.
故答案为:x≠﹣4.
【点评】本题考查了函数的自变量的取值范围,掌握求函数的自变量的取值范围的方法是关键.
7.(2024秋 西湖区期末)如图(1),在△ABC中,∠ACB=90°,点P从点A出发沿A→B→C以1cm/s的速度匀速运动至点C,图(2)是点P运动时,△ACP的面积y(cm2)随时间x(s)变化的函数图象,则△ABC的面积为 2 cm2,周长为 (11) cm.
【考点】动点问题的函数图象.
【专题】函数及其图象;运算能力.
【答案】2;(11).
【分析】依据题意,由x=7时和x=11,分别求出AB、BC,再由∠ACB=90°,可得ACcm,进而可以计算得解.
【解答】解:由题意得,当x=7时,△ACP面积最大,此时AP=AB=7×1=7(cm);当x=11时,△ACP面积为0,此时可得BC=4×1=4(cm).
又∵∠ACB=90°,
∴AC(cm).
∴△ABC的面积为:AC BC42(cm2),周长为7+4(11)(cm).
故答案为:2;(11).
【点评】本题主要考查了动点问题的函数图象,解题时要熟练掌握并能读懂题意列出关系式是关键.
8.(2024秋 包河区期末)某物理学习小组探究甲、乙、丙、丁四种物质的密度,将测量结果数据绘制成如图所示的图象,则四种物质中密度最大的是 甲 .
【考点】函数的图象.
【专题】函数及其图象;几何直观.
【答案】甲.
【分析】根据密度=质量÷体积,从图象中比较每种物质的质量和体积,即可得到答案.
【解答】解:甲和丙的体积相等,
甲的质量>丙的质量,
∴甲的密度大;
乙和丁的体积相等,
乙的质量>丁的质量,
∴乙的密度大;
甲和乙的质量相等,
∵甲的体积<乙的体积,
∴甲的密度大.
故答案为:甲.
【点评】本题考查了函数的图象,解题的关键是根据图象中的信息进行解答.
9.(2024秋 潍坊期末)小亮去超市买生鲜,电子秤的数据显示屏显示重量、单价、金额三个量,则这三个量中的变量是 重量和金额 .
【考点】常量与变量.
【专题】函数及其图象;推理能力.
【答案】重量和金额.
【分析】根据变量的定义判断即可.
【解答】解:∵单价保持不变,金额随着重量的变化而变化,
∴这三个量中的变量是重量和金额.
故答案为:重量和金额.
【点评】本题考查常量与变量,掌握变量的定义是解题的关键.
10.(2024秋 太仓市期末)如图1,底面积为36cm2的空长方体容器内水平放置着由两个实心圆柱体组成的“几何体”,现向容器内均匀注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图2所示,若“几何体”下方圆柱体的底面积为12cm2,则“几何体”上方圆柱体的底面积为 24 cm2.
【考点】函数的图象;认识立体图形;几何体的表面积.
【专题】函数及其图象;应用意识.
【答案】24.
【分析】根据图象,分三个部分:满过“几何体”下方圆柱需18s,满过“几何体”上方圆柱需24﹣18=6(s),注满“几何体”上面的空圆柱形容器需42﹣24=18(s),再设匀速注水的水流速度为x cm3/s,根据圆柱的体积公式列方程可得匀速注水的水流速度;根据圆柱的体积公式得a (36﹣12)=18×8,解得a=6,于是得到“几何体”上方圆柱的高为4cm,设“几何体”上方圆柱的底面积为S cm2,根据圆柱的体积公式得4 (36﹣S)=8×(24﹣18),再解方程即可.
【解答】解:根据函数图象得到圆柱形容器的高为14cm,两个实心圆柱组成的“几何体”的高度为10cm,
水从刚满过由两个实心圆柱组成的“几何体”到注满用了:42﹣24=18(s),
这段高度为:14﹣10=4(cm),
设匀速注水的水流速度为x cm3/s,则18 x=36×4,
解得x=8,
即匀速注水的水流速度为8cm3/s;
“几何体”下方圆柱的高为a,则a (36﹣12)=18×8,
解得a=6,
所以“几何体”上方圆柱的高为10﹣6=4(cm),
设“几何体”上方圆柱的底面积为S cm2,根据题意得4 (36﹣S)=8×(24﹣18),
解得S=24,
即“几何体”上方圆柱的底面积为24cm2.
故答案为:24.
【点评】本题考查了一次函数的应用,正确把分段函数图象中自变量与对应的函数值转化为实际问题中的数量关系,然后运用方程的思想解决实际问题是解题关键.
三.解答题(共5小题)
11.(2024秋 湘桥区期末)在高速公路上,潮州到广州的距离约为420千米,如果行驶速度为v(千米/小时),行驶时间为t(小时),完成下面填空:
(1)
速度v(千米/小时) 60 70 80
时间t(小时) 7 6 4.2
(2)用式子表示v与t之间的关系: vt=420 ,v与t成 反 比例关系.
【考点】函数关系式.
【专题】函数及其图象;应用意识.
【答案】(1)5.25;100;(2)vt=420;反.
【分析】(1)根据“路程=速度×时间”即可作答;
(2)根据“路程=速度×时间”即可作答.
【解答】解:(1)60×7÷80=5.25,
60×7÷4.2=100.
故答案为:5.25;100.
(2)vt=60×7=420,
v与t成反比例关系.
故答案为:vt=420;反.
【点评】本题主要考查函数关系式,熟练掌握“路程=速度×时间”是解题的关键.
12.(2024秋 沙坪坝区校级期末)如图,在四边形ABCD中,AB∥CD,∠B=90°,CD=CB=4,AB=6,点E从点D出发,以每秒1个单位的速度沿折线D→C→B方向运动,点F从点A出发,以每秒个单位的速度沿A→B方向运动,到点B后以每秒1个单位的速度沿B→C方向运动;当两者相遇时停止运动.设运动时间为x秒,△AEF的面积为y.
(1)请直接写出y关于x的函数表达式并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出△AEF面积大于6时,x的取值范围.
【考点】动点问题的函数图象.
【专题】数形结合;分类讨论;应用意识.
【答案】(1)y;
(2)图象见解答部分,当x=4时,y有最大值12或当0≤x≤4时,y随x的增大而增大(答案不唯一,写出一条性质即可);
(3)△AEF面积大于6时,2<x<5.
【分析】(1)分点E、F分别在线段CD和AB上;点E、F都在线段BC上,表示出△AEF的面积即可;
(2)根据自变量的取值范围及对应的函数值画出相应的函数图象,进而表示出函数的最值或者增减性即可;
(3)根据(2)得到的函数图象,看函数值大于6的部分所对应的自变量的取值范围即可.
【解答】解:(1)①0≤x≤4,
由题意得:AFx,
∴yx×4=3x;
②4<x≤6,
点F走到点B处时需要的时间为:64(秒),
∴EF=BC﹣EC﹣BF
=4﹣(x﹣4)﹣(x﹣4)
=12﹣2x,
∴y6×(12﹣2x)=﹣6x+36,
∴y;
(2)
当x=4时,y有最大值12或当0≤x≤4时,y随x的增大而增大(答案不唯一,写出一条性质即可);
(3)△AEF面积大于6时,2<x<5.
【点评】本题考查动点问题的函数图象.根据题意判断出不同时间范围内动点的位置是解决本题的易错点.
13.(2024秋 鼓楼区期末)如图,在长方形电子广告屏ABCD中,AB=8m,BC=6m.画面设计如下:动点P从点A出发沿长方形的边AB,BC以2m/s的速度向点C运动,逐渐展开主体广告画面.
(1)写出△APD的面积S(m2)关于点P的运动时间t(s)的函数表达式;
(2)画出上述函数的图象.
【考点】动点问题的函数图象.
【专题】一次函数及其应用;应用意识.
【答案】(1)S;(2)图象见解析.
【分析】(1)当0≤t≤4时,S△APDAP×AD,当4<t≤7时,S△APDAB×AD,进而得出答案;
(2)根据函数关系式画出图象即可.
【解答】解:(1)当0≤t≤4时,S△APDAP×AD6t,
当4<t≤7时,S△APDAB×AD24,
则△APD的面积S(m2)关于点P的运动时间t(s)的函数表达式为S.
(2)图象见下图:
【点评】本题主要考查动点问题的函数图象,正确写出函数图象是解题的关键.
14.(2024秋 丽水期末)盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如表所示:
重量(单位:千克) 0 2 2.5 3 b
指针转过的角度 0° 36° a° 54° 180°
(1)请直接写出a、b的值;
(2)指针转过的角度不得超过360°,否则盘秤会受损,称量18千克的物品会对盘秤造成损伤吗?说说你的理由.
(3)某顾客在一家水果店购买水果,用这种盘秤称量两次,第二次的数量是第一次数量的2倍多3千克,且指针第二次转过的角度比第一次大108°,该顾客一共购买了多少千克水果.
【考点】函数的表示方法;钟面角;一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】(1)a的值是45,b的值是10;
(2)称量18千克的物品不会对盘秤造成损伤;理由见解答过程;
(3)12千克.
【分析】(1)根据表格中的数据,可以发现每增加1千克,指针转18°,然后即可计算出a、b的值;
(2)先判断,然后根据(1)中的发现计算称量19千克的物品指针转过的角度,再与360°比较大小即可;
(3)根据题意和针第二次转过的角度比第一次大126°,可以列出相应的方程,然后求解即可.
【解答】解:(1)由表格可得:36°÷2=18°,
∴a°=18°×2.5=45°,
b=180°÷18°=10,
即a的值是45,b的值是10;
(2)称量18千克的物品不会对盘秤造成损伤;理由如下:
∵18×18°=324°<360°,
∴称量18千克的物品不会对盘秤造成损伤;
(3)设第一次购买水果x千克,则第二次购买水果(2x+3)千克,
依题意得:(2x+3)﹣x=108°÷18°,
解得x=3,
∴2x+3=9,
∴3+9=12(千克),
答:该顾客一共购买了12千克水果.
【点评】本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
15.(2024秋 浦东新区校级期末)某校科技节启用无人机航拍活动,在操控无人机时可调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 时间(或t) ;
(2)无人机在75米高的上空停留的时间是 5 分钟;
(3)在上升或下降过程中,无人机的速度为 25 米/分;
(4)图中a表示的数是 2 ;b表示的数是 15 ;
(5)图中点A表示的实际意义是 在第6分钟时,无人机的飞行高度为50米 .
【考点】函数的图象;常量与变量.
【专题】函数及其图象;应用意识.
【答案】(1)时间(或t); (2)5; (3)25; (4)2,15;(5)第6分钟时,无人机飞行的高度是50米.
【分析】(1)根据图象信息得出自变量;
(2)根据图象信息得出无人机在75米高的上空停留的时间12﹣7=5分钟即可;
(3)根据“速度=路程÷时间”计算即可;
(4)根据速度、时间与路程的关系列式计算解得即可;
(5)根据点的实际意义解答即可.
【解答】解:(1)横轴是时间,纵轴是高度,所以自变量是时间(或t),因变量是高度(或h);
故答案为:时间(或t);
(2)无人机在75米高的上空停留的时间是12﹣7=5(分钟);
故答案为:5;
(3)在上升或下降过程中,无人机的速度=25(米/分);
故答案为:25;
(4)图中a表示的数是(分钟);b表示的数是(分钟);
故答案为:2,15;
(5)图中点A表示在第6分钟时,无人机的飞行高度为50米;
故答案为:在第6分钟时,无人机的飞行高度为50米.
【点评】此题考查函数图象问题,从图象中获取信息是学习函数的基本功,要结合题意熟练掌握.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 南岸区期末)下面属于定量数据的是( )
A.汽车的产量 B.购买商品的支付方式
C.性别 D.学历
2.(2024秋 南海区期末)你知道为什么冬天电瓶车电池不耐用?因为电瓶车通常使用铅酸电池和锂电池,这两种电池的最佳使用温度都是25摄氏度左右.随着温度降低,电池中的化学物质活性降低,从而导致电池不耐用.在这个变化过程中,自变量是( )
A.化学物质 B.温度 C.电池 D.电瓶车
3.(2025 潍坊模拟)某年部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,中国创新综合排名全球第22名,创新效率排名位于全球( )
A.第4名 B.第3名 C.第2名 D.第1名
4.(2024秋 浦江县期末)【情境】跑步是一种简单而强大的有氧运动,被广泛认为是最佳的锻炼方式.周末小明从家出发跑步去健身主题公园,中途休息一段时间,到达健身公园后又再次休息,之后跑步返回家中,已知小明两次休息时间相同且跑步速度始终不变.小明离开家的路程S与时间t的关系(部分数据)如图所示.
【问题】小明每次休息的时间为( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
5.(2024秋 句容市期末)如图,在长方形ABCD中,AB=5,AD=2,E为边CD上一点,且DE=3,动点P从点A出发,沿路径A→B→C→E运动,则三角形APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )
A. B.
C. D.
二.填空题(共5小题)
6.(2024秋 长春校级期末)在函数中,自变量x的取值范围是 .
7.(2024秋 西湖区期末)如图(1),在△ABC中,∠ACB=90°,点P从点A出发沿A→B→C以1cm/s的速度匀速运动至点C,图(2)是点P运动时,△ACP的面积y(cm2)随时间x(s)变化的函数图象,则△ABC的面积为 cm2,周长为 cm.
8.(2024秋 包河区期末)某物理学习小组探究甲、乙、丙、丁四种物质的密度,将测量结果数据绘制成如图所示的图象,则四种物质中密度最大的是 .
9.(2024秋 潍坊期末)小亮去超市买生鲜,电子秤的数据显示屏显示重量、单价、金额三个量,则这三个量中的变量是 .
10.(2024秋 太仓市期末)如图1,底面积为36cm2的空长方体容器内水平放置着由两个实心圆柱体组成的“几何体”,现向容器内均匀注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图2所示,若“几何体”下方圆柱体的底面积为12cm2,则“几何体”上方圆柱体的底面积为 cm2.
三.解答题(共5小题)
11.(2024秋 湘桥区期末)在高速公路上,潮州到广州的距离约为420千米,如果行驶速度为v(千米/小时),行驶时间为t(小时),完成下面填空:
(1)
速度v(千米/小时) 60 70 80
时间t(小时) 7 6 4.2
(2)用式子表示v与t之间的关系: ,v与t成 比例关系.
12.(2024秋 沙坪坝区校级期末)如图,在四边形ABCD中,AB∥CD,∠B=90°,CD=CB=4,AB=6,点E从点D出发,以每秒1个单位的速度沿折线D→C→B方向运动,点F从点A出发,以每秒个单位的速度沿A→B方向运动,到点B后以每秒1个单位的速度沿B→C方向运动;当两者相遇时停止运动.设运动时间为x秒,△AEF的面积为y.
(1)请直接写出y关于x的函数表达式并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出△AEF面积大于6时,x的取值范围.
13.(2024秋 鼓楼区期末)如图,在长方形电子广告屏ABCD中,AB=8m,BC=6m.画面设计如下:动点P从点A出发沿长方形的边AB,BC以2m/s的速度向点C运动,逐渐展开主体广告画面.
(1)写出△APD的面积S(m2)关于点P的运动时间t(s)的函数表达式;
(2)画出上述函数的图象.
14.(2024秋 丽水期末)盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如表所示:
重量(单位:千克) 0 2 2.5 3 b
指针转过的角度 0° 36° a° 54° 180°
(1)请直接写出a、b的值;
(2)指针转过的角度不得超过360°,否则盘秤会受损,称量18千克的物品会对盘秤造成损伤吗?说说你的理由.
(3)某顾客在一家水果店购买水果,用这种盘秤称量两次,第二次的数量是第一次数量的2倍多3千克,且指针第二次转过的角度比第一次大108°,该顾客一共购买了多少千克水果.
15.(2024秋 浦东新区校级期末)某校科技节启用无人机航拍活动,在操控无人机时可调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 ;
(2)无人机在75米高的上空停留的时间是 分钟;
(3)在上升或下降过程中,无人机的速度为 米/分;
(4)图中a表示的数是 ;b表示的数是 ;
(5)图中点A表示的实际意义是 .
期末专项培优 函数
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 南岸区期末)下面属于定量数据的是( )
A.汽车的产量 B.购买商品的支付方式
C.性别 D.学历
【考点】常量与变量.
【专题】数与式;应用意识.
【答案】A
【分析】定性数据:也称为分类数据,是非数值型的数据,描述事物的特征或属性.通常以文字、符号或类别来表示,不具备数值意义;定量数据:也称为连续数据或数值型数据,是数值型的数据,可以进行数值计算和统计分析,据此进行判断即可.
【解答】解:定性数据:也称为分类数据,是非数值型的数据,定量数据:也称为连续数据或数值型数据,是数值型的数据,由此可得:
A、汽车的产量,为定量数据,符合题意;
B、购买商品的支付方式,为定性数据,不符合题意;
C、性别,为定性数据,不符合题意;
D、学历,为定性数据,不符合题意.
故选:A.
【点评】本题考查定量数据和定性数据,正确记忆相关定义是解题关键.
2.(2024秋 南海区期末)你知道为什么冬天电瓶车电池不耐用?因为电瓶车通常使用铅酸电池和锂电池,这两种电池的最佳使用温度都是25摄氏度左右.随着温度降低,电池中的化学物质活性降低,从而导致电池不耐用.在这个变化过程中,自变量是( )
A.化学物质 B.温度 C.电池 D.电瓶车
【考点】常量与变量.
【专题】函数及其图象;数感.
【答案】B
【分析】在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量,据此进行判断即可.
【解答】解:随着温度降低,电池中的化学物质活性降低,从而导致电池不耐用.在这个变化过程中,自变量是温度,
故选:B.
【点评】本题考查常量与变量,熟练掌握其定义是解题的关键.
3.(2025 潍坊模拟)某年部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,中国创新综合排名全球第22名,创新效率排名位于全球( )
A.第4名 B.第3名 C.第2名 D.第1名
【考点】函数的图象.
【专题】函数及其图象;几何直观.
【答案】B
【分析】根据中国创新综合排名全球第22名,在坐标系中找到对应的中国创新产出排名为第11名,再根据中国创新产出排名为第11名在另一排名中找到创新效率排名为第3名即可.
【解答】解:如图,
由左图得,中国创新综合排名全球第22名,在坐标系中找到对应的中国创新产出排名为第11名,
由右图得,中国创新产出排名为第11名,创新效率排名为第3名.
故选:B.
【点评】本题考查函数的图象,理解题意是解题的关键.
4.(2024秋 浦江县期末)【情境】跑步是一种简单而强大的有氧运动,被广泛认为是最佳的锻炼方式.周末小明从家出发跑步去健身主题公园,中途休息一段时间,到达健身公园后又再次休息,之后跑步返回家中,已知小明两次休息时间相同且跑步速度始终不变.小明离开家的路程S与时间t的关系(部分数据)如图所示.
【问题】小明每次休息的时间为( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
【考点】函数的图象.
【专题】函数及其图象;运算能力.
【答案】B
【分析】先求出跑步速度,再求出跑步返回家中所用的时间,根据两次休息时间相同且跑步速度始终不变,即可求解.
【解答】解:由题意,小明跑步速度为(米/分钟),
跑步返回家中所用的时间为15(分钟),
∴小明每次休息的时间为(50﹣15×2)=10(分钟),
故选:B.
【点评】本题考查了函数的图象,理解题意,从函数图象中获取有用信息是解题的关键.
5.(2024秋 句容市期末)如图,在长方形ABCD中,AB=5,AD=2,E为边CD上一点,且DE=3,动点P从点A出发,沿路径A→B→C→E运动,则三角形APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )
A. B.
C. D.
【考点】动点问题的函数图象.
【专题】函数及其图象;几何直观;推理能力.
【答案】D
【分析】求出CE的长,然后分三种情况讨论:①点P在AB上运动时,利用三角形的面积公式列式得到y与x的关系式;②点P在BC上运动时,根据S△APE=S梯形ABCE﹣S△ABP﹣S△ECP式整理得到y与x的关系式;③点P在CE上运动时,利用三角形的面积公式列式得到y与x的函数关系,根据解析式即可得到函数的图象.
【解答】解:在长方形ABCD中,AB=5,AD=2,
∴BC=AD=2,CD=AB=5,
∴CE=CD﹣DE=5﹣3=2,
动点P从点A出发,沿路径A→B→C→E运动,当点P在AB上运动,即0≤x≤5时,AP=x,
,
∴y=x(0≤x≤5),
当点P在BC上运动,即5<x≤7时,
BP=x﹣5,CP=5+2﹣x=7﹣x,
∴S△APE=S梯形ABCE﹣S△ABP﹣S△ECP
,
∴(5<x≤7),
当点P在CE上运动,即7<x≤9时,CP=x﹣5﹣2=x﹣7,
EP=EC﹣CP=2﹣(x﹣7)=9﹣x,
∴,
∴y=9﹣x(7<x≤9),
综上所述,函数关系式为,
∴当x=5时,y=5;
当x=7时,y=2;
当x=9时,y=0.
∴选项D的图象符合题意.
故选:D.
【点评】本题考查了动点问题函数图象,读懂题目信息,根据点P的位置的不同分三段列式求出y与x的关系式是解题的关键.
二.填空题(共5小题)
6.(2024秋 长春校级期末)在函数中,自变量x的取值范围是 x≠﹣4 .
【考点】函数自变量的取值范围.
【专题】函数及其图象;运算能力.
【答案】见试题解答内容
【分析】根据分式有意义的条件得出x+4≠0,求解即可.
【解答】解:根据分式有意义的条件可知,x+4≠0,
解得:x≠﹣4.
故答案为:x≠﹣4.
【点评】本题考查了函数的自变量的取值范围,掌握求函数的自变量的取值范围的方法是关键.
7.(2024秋 西湖区期末)如图(1),在△ABC中,∠ACB=90°,点P从点A出发沿A→B→C以1cm/s的速度匀速运动至点C,图(2)是点P运动时,△ACP的面积y(cm2)随时间x(s)变化的函数图象,则△ABC的面积为 2 cm2,周长为 (11) cm.
【考点】动点问题的函数图象.
【专题】函数及其图象;运算能力.
【答案】2;(11).
【分析】依据题意,由x=7时和x=11,分别求出AB、BC,再由∠ACB=90°,可得ACcm,进而可以计算得解.
【解答】解:由题意得,当x=7时,△ACP面积最大,此时AP=AB=7×1=7(cm);当x=11时,△ACP面积为0,此时可得BC=4×1=4(cm).
又∵∠ACB=90°,
∴AC(cm).
∴△ABC的面积为:AC BC42(cm2),周长为7+4(11)(cm).
故答案为:2;(11).
【点评】本题主要考查了动点问题的函数图象,解题时要熟练掌握并能读懂题意列出关系式是关键.
8.(2024秋 包河区期末)某物理学习小组探究甲、乙、丙、丁四种物质的密度,将测量结果数据绘制成如图所示的图象,则四种物质中密度最大的是 甲 .
【考点】函数的图象.
【专题】函数及其图象;几何直观.
【答案】甲.
【分析】根据密度=质量÷体积,从图象中比较每种物质的质量和体积,即可得到答案.
【解答】解:甲和丙的体积相等,
甲的质量>丙的质量,
∴甲的密度大;
乙和丁的体积相等,
乙的质量>丁的质量,
∴乙的密度大;
甲和乙的质量相等,
∵甲的体积<乙的体积,
∴甲的密度大.
故答案为:甲.
【点评】本题考查了函数的图象,解题的关键是根据图象中的信息进行解答.
9.(2024秋 潍坊期末)小亮去超市买生鲜,电子秤的数据显示屏显示重量、单价、金额三个量,则这三个量中的变量是 重量和金额 .
【考点】常量与变量.
【专题】函数及其图象;推理能力.
【答案】重量和金额.
【分析】根据变量的定义判断即可.
【解答】解:∵单价保持不变,金额随着重量的变化而变化,
∴这三个量中的变量是重量和金额.
故答案为:重量和金额.
【点评】本题考查常量与变量,掌握变量的定义是解题的关键.
10.(2024秋 太仓市期末)如图1,底面积为36cm2的空长方体容器内水平放置着由两个实心圆柱体组成的“几何体”,现向容器内均匀注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图2所示,若“几何体”下方圆柱体的底面积为12cm2,则“几何体”上方圆柱体的底面积为 24 cm2.
【考点】函数的图象;认识立体图形;几何体的表面积.
【专题】函数及其图象;应用意识.
【答案】24.
【分析】根据图象,分三个部分:满过“几何体”下方圆柱需18s,满过“几何体”上方圆柱需24﹣18=6(s),注满“几何体”上面的空圆柱形容器需42﹣24=18(s),再设匀速注水的水流速度为x cm3/s,根据圆柱的体积公式列方程可得匀速注水的水流速度;根据圆柱的体积公式得a (36﹣12)=18×8,解得a=6,于是得到“几何体”上方圆柱的高为4cm,设“几何体”上方圆柱的底面积为S cm2,根据圆柱的体积公式得4 (36﹣S)=8×(24﹣18),再解方程即可.
【解答】解:根据函数图象得到圆柱形容器的高为14cm,两个实心圆柱组成的“几何体”的高度为10cm,
水从刚满过由两个实心圆柱组成的“几何体”到注满用了:42﹣24=18(s),
这段高度为:14﹣10=4(cm),
设匀速注水的水流速度为x cm3/s,则18 x=36×4,
解得x=8,
即匀速注水的水流速度为8cm3/s;
“几何体”下方圆柱的高为a,则a (36﹣12)=18×8,
解得a=6,
所以“几何体”上方圆柱的高为10﹣6=4(cm),
设“几何体”上方圆柱的底面积为S cm2,根据题意得4 (36﹣S)=8×(24﹣18),
解得S=24,
即“几何体”上方圆柱的底面积为24cm2.
故答案为:24.
【点评】本题考查了一次函数的应用,正确把分段函数图象中自变量与对应的函数值转化为实际问题中的数量关系,然后运用方程的思想解决实际问题是解题关键.
三.解答题(共5小题)
11.(2024秋 湘桥区期末)在高速公路上,潮州到广州的距离约为420千米,如果行驶速度为v(千米/小时),行驶时间为t(小时),完成下面填空:
(1)
速度v(千米/小时) 60 70 80
时间t(小时) 7 6 4.2
(2)用式子表示v与t之间的关系: vt=420 ,v与t成 反 比例关系.
【考点】函数关系式.
【专题】函数及其图象;应用意识.
【答案】(1)5.25;100;(2)vt=420;反.
【分析】(1)根据“路程=速度×时间”即可作答;
(2)根据“路程=速度×时间”即可作答.
【解答】解:(1)60×7÷80=5.25,
60×7÷4.2=100.
故答案为:5.25;100.
(2)vt=60×7=420,
v与t成反比例关系.
故答案为:vt=420;反.
【点评】本题主要考查函数关系式,熟练掌握“路程=速度×时间”是解题的关键.
12.(2024秋 沙坪坝区校级期末)如图,在四边形ABCD中,AB∥CD,∠B=90°,CD=CB=4,AB=6,点E从点D出发,以每秒1个单位的速度沿折线D→C→B方向运动,点F从点A出发,以每秒个单位的速度沿A→B方向运动,到点B后以每秒1个单位的速度沿B→C方向运动;当两者相遇时停止运动.设运动时间为x秒,△AEF的面积为y.
(1)请直接写出y关于x的函数表达式并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,直接写出△AEF面积大于6时,x的取值范围.
【考点】动点问题的函数图象.
【专题】数形结合;分类讨论;应用意识.
【答案】(1)y;
(2)图象见解答部分,当x=4时,y有最大值12或当0≤x≤4时,y随x的增大而增大(答案不唯一,写出一条性质即可);
(3)△AEF面积大于6时,2<x<5.
【分析】(1)分点E、F分别在线段CD和AB上;点E、F都在线段BC上,表示出△AEF的面积即可;
(2)根据自变量的取值范围及对应的函数值画出相应的函数图象,进而表示出函数的最值或者增减性即可;
(3)根据(2)得到的函数图象,看函数值大于6的部分所对应的自变量的取值范围即可.
【解答】解:(1)①0≤x≤4,
由题意得:AFx,
∴yx×4=3x;
②4<x≤6,
点F走到点B处时需要的时间为:64(秒),
∴EF=BC﹣EC﹣BF
=4﹣(x﹣4)﹣(x﹣4)
=12﹣2x,
∴y6×(12﹣2x)=﹣6x+36,
∴y;
(2)
当x=4时,y有最大值12或当0≤x≤4时,y随x的增大而增大(答案不唯一,写出一条性质即可);
(3)△AEF面积大于6时,2<x<5.
【点评】本题考查动点问题的函数图象.根据题意判断出不同时间范围内动点的位置是解决本题的易错点.
13.(2024秋 鼓楼区期末)如图,在长方形电子广告屏ABCD中,AB=8m,BC=6m.画面设计如下:动点P从点A出发沿长方形的边AB,BC以2m/s的速度向点C运动,逐渐展开主体广告画面.
(1)写出△APD的面积S(m2)关于点P的运动时间t(s)的函数表达式;
(2)画出上述函数的图象.
【考点】动点问题的函数图象.
【专题】一次函数及其应用;应用意识.
【答案】(1)S;(2)图象见解析.
【分析】(1)当0≤t≤4时,S△APDAP×AD,当4<t≤7时,S△APDAB×AD,进而得出答案;
(2)根据函数关系式画出图象即可.
【解答】解:(1)当0≤t≤4时,S△APDAP×AD6t,
当4<t≤7时,S△APDAB×AD24,
则△APD的面积S(m2)关于点P的运动时间t(s)的函数表达式为S.
(2)图象见下图:
【点评】本题主要考查动点问题的函数图象,正确写出函数图象是解题的关键.
14.(2024秋 丽水期末)盘秤是一种常见的称量工具,指针转过的角度与被称物体的重量有一定的关系,如表所示:
重量(单位:千克) 0 2 2.5 3 b
指针转过的角度 0° 36° a° 54° 180°
(1)请直接写出a、b的值;
(2)指针转过的角度不得超过360°,否则盘秤会受损,称量18千克的物品会对盘秤造成损伤吗?说说你的理由.
(3)某顾客在一家水果店购买水果,用这种盘秤称量两次,第二次的数量是第一次数量的2倍多3千克,且指针第二次转过的角度比第一次大108°,该顾客一共购买了多少千克水果.
【考点】函数的表示方法;钟面角;一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】(1)a的值是45,b的值是10;
(2)称量18千克的物品不会对盘秤造成损伤;理由见解答过程;
(3)12千克.
【分析】(1)根据表格中的数据,可以发现每增加1千克,指针转18°,然后即可计算出a、b的值;
(2)先判断,然后根据(1)中的发现计算称量19千克的物品指针转过的角度,再与360°比较大小即可;
(3)根据题意和针第二次转过的角度比第一次大126°,可以列出相应的方程,然后求解即可.
【解答】解:(1)由表格可得:36°÷2=18°,
∴a°=18°×2.5=45°,
b=180°÷18°=10,
即a的值是45,b的值是10;
(2)称量18千克的物品不会对盘秤造成损伤;理由如下:
∵18×18°=324°<360°,
∴称量18千克的物品不会对盘秤造成损伤;
(3)设第一次购买水果x千克,则第二次购买水果(2x+3)千克,
依题意得:(2x+3)﹣x=108°÷18°,
解得x=3,
∴2x+3=9,
∴3+9=12(千克),
答:该顾客一共购买了12千克水果.
【点评】本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
15.(2024秋 浦东新区校级期末)某校科技节启用无人机航拍活动,在操控无人机时可调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 时间(或t) ;
(2)无人机在75米高的上空停留的时间是 5 分钟;
(3)在上升或下降过程中,无人机的速度为 25 米/分;
(4)图中a表示的数是 2 ;b表示的数是 15 ;
(5)图中点A表示的实际意义是 在第6分钟时,无人机的飞行高度为50米 .
【考点】函数的图象;常量与变量.
【专题】函数及其图象;应用意识.
【答案】(1)时间(或t); (2)5; (3)25; (4)2,15;(5)第6分钟时,无人机飞行的高度是50米.
【分析】(1)根据图象信息得出自变量;
(2)根据图象信息得出无人机在75米高的上空停留的时间12﹣7=5分钟即可;
(3)根据“速度=路程÷时间”计算即可;
(4)根据速度、时间与路程的关系列式计算解得即可;
(5)根据点的实际意义解答即可.
【解答】解:(1)横轴是时间,纵轴是高度,所以自变量是时间(或t),因变量是高度(或h);
故答案为:时间(或t);
(2)无人机在75米高的上空停留的时间是12﹣7=5(分钟);
故答案为:5;
(3)在上升或下降过程中,无人机的速度=25(米/分);
故答案为:25;
(4)图中a表示的数是(分钟);b表示的数是(分钟);
故答案为:2,15;
(5)图中点A表示在第6分钟时,无人机的飞行高度为50米;
故答案为:在第6分钟时,无人机的飞行高度为50米.
【点评】此题考查函数图象问题,从图象中获取信息是学习函数的基本功,要结合题意熟练掌握.
21世纪教育网(www.21cnjy.com)
