【期末专项培优】平行四边形(含解析)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 【期末专项培优】平行四边形(含解析)2024-2025学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 941.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 10:06:49 | ||
图片预览




文档简介
期末专项培优 平行四边形
一.选择题(共5小题)
1.(2024秋 长春校级期末)如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=CD B.AD=BC
C.AB=BC D.∠B+∠C=180°
2.(2024秋 长春校级期末)如图,在 ABCD中,∠ADC的平分线DE交BC于点E,若AB=11,BE=4,则AD的长为( )
A.15 B.11 C.20 D.52
3.(2025 山东模拟)如图,在平行四边形ABCD中,点M为边AD上一点,AM=2DM,BM平分∠ABC,点E,F分别是BM,CM的中点,若EF=3cm,则AB的长为( )
A.5.5cm B.5cm C.4.5cm D.4cm
4.(2024秋 丽水期末)如图,在 ABCD中,AB=4,BC=6,∠B=45°,E是BC边上的动点,连结DE,过点A作AF⊥DE于点F.则DE AF的值是( )
A. B. C.12 D.6
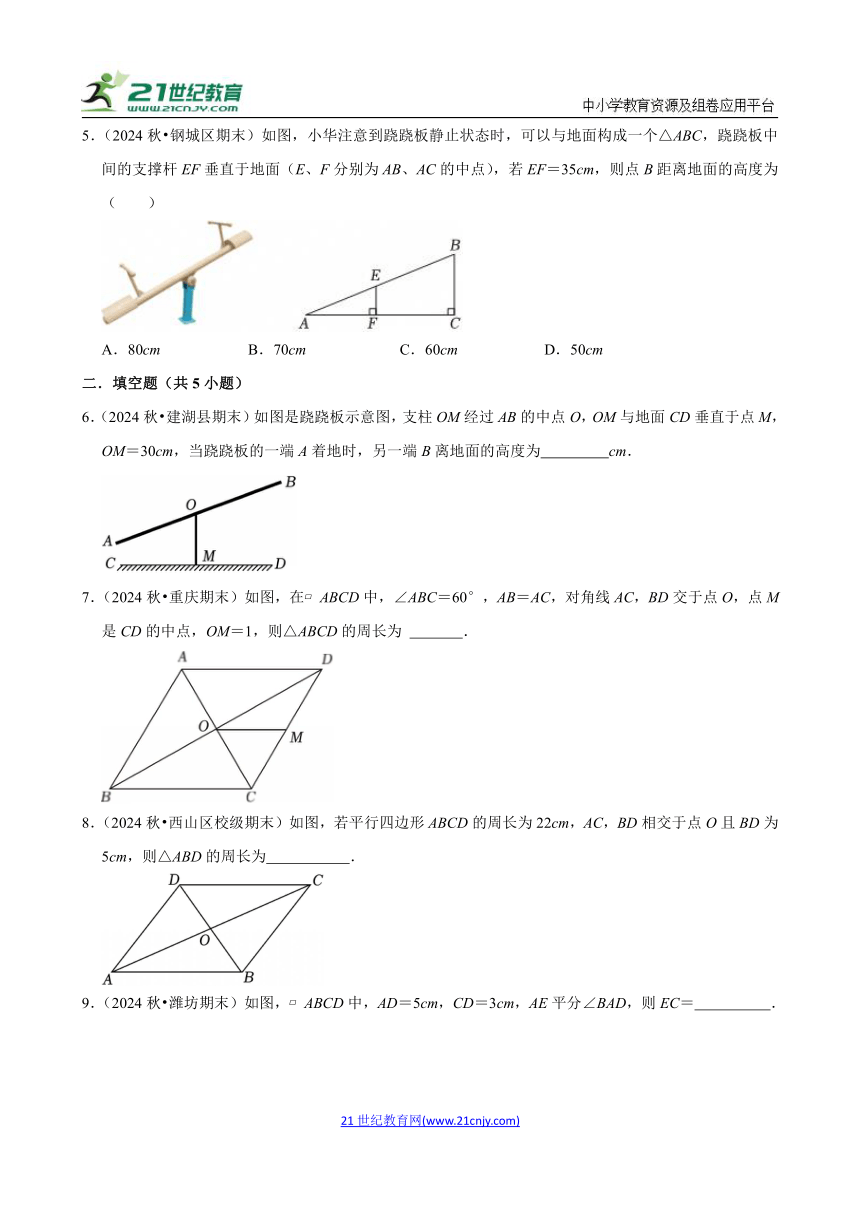
5.(2024秋 钢城区期末)如图,小华注意到跷跷板静止状态时,可以与地面构成一个△ABC,跷跷板中间的支撑杆EF垂直于地面(E、F分别为AB、AC的中点),若EF=35cm,则点B距离地面的高度为( )
A.80cm B.70cm C.60cm D.50cm
二.填空题(共5小题)
6.(2024秋 建湖县期末)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=30cm,当跷跷板的一端A着地时,另一端B离地面的高度为 cm.
7.(2024秋 重庆期末)如图,在 ABCD中,∠ABC=60°,AB=AC,对角线AC,BD交于点O,点M是CD的中点,OM=1,则△ABCD的周长为 .
8.(2024秋 西山区校级期末)如图,若平行四边形ABCD的周长为22cm,AC,BD相交于点O且BD为5cm,则△ABD的周长为 .
9.(2024秋 潍坊期末)如图, ABCD中,AD=5cm,CD=3cm,AE平分∠BAD,则EC= .
10.(2024秋 鲤城区校级期末)如图,在 ABCD中,对角线AC,BD交于点O,AC⊥CD,过点O作OE⊥AC交AD于点E,连接CE.已知AC=6,BD=10,则△CDE的周长是 .
三.解答题(共5小题)
11.(2024秋 长春校级期末)四边形ABCD中,DE⊥AC,BF⊥AC,且DE=BF,AF=CE.
(1)求证:四边形ABCD是平行四边形;
(2)若DE=4,CF=3,EF=5,则四边形ABCD的面积为 .
12.(2024秋 厦门期末)如图,四边形ABCD是平行四边形,AE⊥BC且交CB的延长线于点E,DF⊥BC于点F.证明BE=CF.
13.(2024秋 紫金县期末)如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,BD=DE=2,求四边形BEDF的面积.
14.(2024秋 钢城区期末)如图,在四边形ABCD中,AD=6,BC=16,AD∥BC,AB=8,∠ABC=60°,点E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.设运动时间为t秒.
(1)线段PD= ;CQ= ;QE= (用含t的代数式表示);
(2)当t为何值时,以点P,Q,E,D为顶点的四边形是平行四边形?
15.(2024秋 沙坪坝区校级期末)如图,在平行四边形ABCD中,AC与BD相交于点O,延长CD至点E,使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AC平分∠BAE,AC=8,AE=6,求△ACE的面积.
期末专项培优 平行四边形
参考答案与试题解析
题号 1 2 3 4 5
答案 A A D A B
一.选择题(共5小题)
1.(2024秋 长春校级期末)如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=CD B.AD=BC
C.AB=BC D.∠B+∠C=180°
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【答案】A
【分析】由AB∥CD,AB=CD,根据“一组对边平行且相等的四边形是平行四边形”证明四边形ABCD是平行四边形,可判断A符合题意;由AB∥CD,AD=BC,可知四边形ABCD是平行四边形或等腰梯形,而不能判定四边形ABCD是平行四边形,可判断B不符合题意;由AB∥CD,AB=BC,不能判定四边形ABCD是平行四边形,可判断C不符合题意;由AB∥CD,得∠B+∠C=180°,可知由AB∥CD,∠B+∠C=180°,不能判定四边形ABCD是平行四边形,可判断D不符合题意,于是得到问题的答案.
【解答】解:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
故A符合题意;
∵AB∥CD,AD=BC,
∴四边形ABCD是平行四边形或等腰梯形,
∴不能判定四边形ABCD是平行四边形,
故B不符合题意;
∵由AB∥CD,AB=BC,不能推导出AB=CD,
∴不能判定四边形ABCD是平行四边形,
故C不符合题意;
∵AB∥CD,
∴∠B+∠C=180°,
∴由AB∥CD,∠B+∠C=180°,不能判定四边形ABCD是平行四边形,
故D不符合题意,
故选:A.
【点评】此题重点考查平行四边形的判定,正确理解和运用平行四边形的判定定理是解题的关键.
2.(2024秋 长春校级期末)如图,在 ABCD中,∠ADC的平分线DE交BC于点E,若AB=11,BE=4,则AD的长为( )
A.15 B.11 C.20 D.52
【考点】平行四边形的性质;角平分线的定义;等腰三角形的判定.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】A
【分析】由∠ADC的平分线DE交BC于点E,得∠ADE=∠CDE,由平行四边形的性质得CD=AB=11,AD∥BC,则∠ADE=∠CED,所以∠CDE=∠CED,则CE=CD=11,求得AD=CB=CE+BE=15,于是得到问题的答案.
【解答】解:∵∠ADC的平分线DE交BC于点E,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,AB=11,
∴CD=AB=11,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD=11,
∵BE=4,
∴AD=CB=CE+BE=11+4=15,
故选:A.
【点评】此题重点考查角平分线的定义、平行四边形的性质、等腰三角形的判定等知识,推导出∠CDE=∠CED是解题的关键.
3.(2025 山东模拟)如图,在平行四边形ABCD中,点M为边AD上一点,AM=2DM,BM平分∠ABC,点E,F分别是BM,CM的中点,若EF=3cm,则AB的长为( )
A.5.5cm B.5cm C.4.5cm D.4cm
【考点】平行四边形的性质;三角形中位线定理.
【专题】多边形与平行四边形;推理能力.
【答案】D
【分析】根据三角形中位线定理和平行四边形的性质即可得到结论.
【解答】解:∵点E,点F分别是BM,CM中点,
∴EF是△BCM的中位线,
∵EF=3cm,
∴BC=2EF=6cm,
∵四边形ABCD是平行四边形,
∴AD=BC=6cm,
∵AD∥BC,
∴∠AMB=∠MBC,
∵BM平分∠ABC,
∴∠ABM=∠MBC,
∴∠AMB=∠ABM,
∴AM=AB,
∵AM=2MD,
∴AM=ABAD=4cm,
故选:D.
【点评】本题考查了平行四边形的性质,三角形中位线定理,熟练掌握平行四边形的性质是解题的关键.
4.(2024秋 丽水期末)如图,在 ABCD中,AB=4,BC=6,∠B=45°,E是BC边上的动点,连结DE,过点A作AF⊥DE于点F.则DE AF的值是( )
A. B. C.12 D.6
【考点】平行四边形的性质.
【专题】多边形与平行四边形;运算能力;推理能力.
【答案】A
【分析】过A作AH⊥BC于H,由等腰直角三角形的性质求出AHAB=2,由平行四边形的性质推出AD∥BC,AD=BC=6,由三角形面积公式得到DE AF=AD AH=12.
【解答】解:过A作AH⊥BC于H,
∵∠B=45°,
∴△ABH是等腰直角三角形,
∴AHAB4=2,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6,
∵AF⊥DE,
∴△EAD的面积AD AHDE AF,
∴DE AF=6×212.
故选:A.
【点评】本题考查平行四边形的性质,三角形的面积,关键是由三角形面积公式得到AD AH=DE AF.
5.(2024秋 钢城区期末)如图,小华注意到跷跷板静止状态时,可以与地面构成一个△ABC,跷跷板中间的支撑杆EF垂直于地面(E、F分别为AB、AC的中点),若EF=35cm,则点B距离地面的高度为( )
A.80cm B.70cm C.60cm D.50cm
【考点】三角形中位线定理.
【专题】三角形;推理能力.
【答案】B
【分析】根据三角形中位线定理即可解决问题.
【解答】解:∵E、F分别为AB、AC的中点,EF=35cm,
∴BC=2EF=70(cm),
∴点B距离地面的高度为70cm.
故选:B.
【点评】本题考查三角形中位线定理,解决本题的关键是掌握三角形的中位线平行于第三边并且等于第三边的一半.
二.填空题(共5小题)
6.(2024秋 建湖县期末)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=30cm,当跷跷板的一端A着地时,另一端B离地面的高度为 60 cm.
【考点】三角形中位线定理.
【专题】三角形;推理能力;应用意识.
【答案】60.
【分析】判断出OM是△ABE的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BE=2OM.
【解答】解:∵O是AB的中点,OM垂直于地面,BE垂直于地面,
∴OM∥BE,
∴OM是△ABE的中位线,
∴BE=2OM=2×30=60(cm),
另一端B离地面的高度为60cm,
故答案为:60.
【点评】本题考查了三角形中位线定理,熟记定理是解题的关键.
7.(2024秋 重庆期末)如图,在 ABCD中,∠ABC=60°,AB=AC,对角线AC,BD交于点O,点M是CD的中点,OM=1,则△ABCD的周长为 8 .
【考点】平行四边形的性质;等腰三角形的性质;等边三角形的性质;三角形中位线定理.
【专题】多边形与平行四边形;推理能力.
【答案】8.
【分析】根据平行四边形的性质得出OB=OD,进而利用三角形中位线定理得出BC=2OM,进而利用等边三角形的性质解答即可.
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD,AB=CD,OB=OD,
∵点M是CD的中点,
∴OM是△DBC的中位线,
∴BC=2OM=2,
∵∠ABC=60°,AB=AC,
∴△ABC是等边三角形,
∴AB=AC=BC=2,
∴ ABCD的周长=2×4=8,
故答案为:8.
【点评】此题考查平行四边形的性质,关键是根据平行四边形的性质得出OB=OD解答.
8.(2024秋 西山区校级期末)如图,若平行四边形ABCD的周长为22cm,AC,BD相交于点O且BD为5cm,则△ABD的周长为 16cm .
【考点】平行四边形的性质.
【专题】多边形与平行四边形;几何直观;推理能力.
【答案】16cm.
【分析】根据平行四边形的性质得到AD=BC,CD=AB,求出AD+AB=11cm,再结合BD=5cm即可解答.
【解答】解:∵平行四边形ABCD的周长为22cm,
∴AD=BC,CD=AB,AD+AB+BC+CD=22cm,
∴AD+AB=11cm,
∵AC,BD相交于点O且BD为5cm,
∴△ABD的周长为:AD+AB+BD=11+5=16(cm),
故答案为:16cm.
【点评】本题考查了平行四边形的性质,解答本题的关键是熟练掌握平行四边形的对边相等.
9.(2024秋 潍坊期末)如图, ABCD中,AD=5cm,CD=3cm,AE平分∠BAD,则EC= 2cm .
【考点】平行四边形的性质;角平分线的定义;平行线的性质;等腰三角形的判定.
【专题】多边形与平行四边形;推理能力.
【答案】2cm.
【分析】根据平行四边形的性质证明∠BAE=BAE,得BE=AB=3cm,然后根据线段的和差即可解决问题.
【解答】解:在 ABCD中,BC=AD=5cm,AB=CD=3cm,AD∥BC,
∵AE平分∠BAD,
∴∠BAE=DAE,
∵AD∥BC,
∴∠BEA=DAE,
∴∠BAE=BAE,
∴BE=AB=3cm,
∴CE=BC﹣BE=5﹣3=2(cm),
故答案为:2cm.
【点评】本题考查平行四边形的性质,角平分线定义,平行线的性质,等腰三角形的判定,解决本题的关键是得到BE=AB.
10.(2024秋 鲤城区校级期末)如图,在 ABCD中,对角线AC,BD交于点O,AC⊥CD,过点O作OE⊥AC交AD于点E,连接CE.已知AC=6,BD=10,则△CDE的周长是 4+2 .
【考点】平行四边形的性质;线段垂直平分线的性质.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】4+2.
【分析】由平行四边形的性质得OC=OAAC=3,OD=OBBD=5,而AC⊥CD,OE⊥AC,则∠ACD=90°,AE=CE,所以CD4,则AD2,再证明∠ECD=∠EDC,所以DE=CE=AEAD,即可求得△CDE的周长为4+2,于是得到问题的答案.
【解答】解:∵四边ABCD是平行四边形,对角线AC、BD交于点O,AC=6,BD=10,
∴OC=OAAC=3,OD=OBBD=5,
∵AC⊥CD,OE⊥AC,
∴∠ACD=90°,AE=CE,
∴CD4,
∴AD2,
∵∠ECD+∠ECA=90°,∠EDC+∠EAC=90°,∠ECA=∠EAC,
∴∠ECD=∠EDC,
∴DE=CE=AEAD,
∴△CDE的周长=CD+DE+CE=44+2,
∴故答案为:4+2.
【点评】此题重点考查平行四边形的性质、线段的垂直平分线的性质、等角的余角相等、勾股定理等知识,证明DE=CE=AE是解题的关键.
三.解答题(共5小题)
11.(2024秋 长春校级期末)四边形ABCD中,DE⊥AC,BF⊥AC,且DE=BF,AF=CE.
(1)求证:四边形ABCD是平行四边形;
(2)若DE=4,CF=3,EF=5,则四边形ABCD的面积为 44 .
【考点】平行四边形的判定与性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】(1)见解析;
(2)44.
【分析】(1)证△ABF≌△CDE(SAS),得AB=CD,∠BAF=∠DCE,再证AB∥CD,然后由平行四边形的判定即可得出结论;
(2)根据全等三角形的性质和三角形的面积公式即可得出结论.
【解答】(1)证明:∵DE⊥AC,BF⊥AC,
∴∠CED=∠AFB=90°,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS),
∴AB=CD,∠BAF=∠DCE,
∴AB∥CD,
∴四边形ABCD是平行四边形;
(2)解:∵CF=3,EF=5,
∴AC=AE+EF+CF=11,
∵DE⊥AC,BF⊥AC,
∴四边形ABCD的面积=2S△ABC=211×4=44,
故答案为:44.
【点评】本题考查了平行四边形的判定与性质、全等三角形的判定与性质以及勾股定理等知识,熟练掌握平行四边形的判定与性质,证明三角形全等是解题的关键.
12.(2024秋 厦门期末)如图,四边形ABCD是平行四边形,AE⊥BC且交CB的延长线于点E,DF⊥BC于点F.证明BE=CF.
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】证明见解答.
【分析】由平行四边形的性质得AB∥DC,AB=DC,则∠ABE=∠C,而∠E=∠DFC=90°,即可根据“AAS“证明△ABE≌△DCF,则BE=CF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠ABE=∠C,
∵AE⊥BC且交CB的延长线于点E,DF⊥BC于点F,
∴∠E=∠DFC=90°,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴BE=CF.
【点评】此题重点考查平行四边形的性质、全等三角形的判定与性质等知识,证明△ABE≌△DCF是解题的关键.
13.(2024秋 紫金县期末)如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,BD=DE=2,求四边形BEDF的面积.
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】多边形与平行四边形;推理能力.
【答案】(1)见解答;
(2)2.
【分析】(1)根据“SAS”及平行四边形的性质证明;
(2)根据勾股定理及平行四边形的判定和性质求解.
【解答】(1)证明:在 ABCD中,有AD=BC,AB=CD,∠A=∠C,
∵E,F分别为边AB,CD的中点,
∴AEAB,CFCD,
∴AE=CF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)解:∵∠ADB=90°,E,为边AB的中点,
∴DEAB=2,
∴AB=4,
∴AD2,
∴S△ABDAD DB=2,
∴S△BDE,
在 ABCD中,有AB=CD,AB∥CD,
∵E,F分别为边AB,CD的中点,
∴AEAB,CFCD,
∴AE=CF,
∴四边形BEDF为平行四边形,
∴S BEDF=2S△BDE=2.
【点评】本题考查了平行四边形的性质,掌握平行四边形的性质及全等三角形的判定和性质是解题的关键.
14.(2024秋 钢城区期末)如图,在四边形ABCD中,AD=6,BC=16,AD∥BC,AB=8,∠ABC=60°,点E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.设运动时间为t秒.
(1)线段PD= 6﹣t ;CQ= 2t ;QE= 8﹣2t(0<t<4)或2t﹣8(4<t<6) (用含t的代数式表示);
(2)当t为何值时,以点P,Q,E,D为顶点的四边形是平行四边形?
【考点】平行四边形的判定;列代数式.
【专题】行程问题;整式;多边形与平行四边形;运算能力;推理能力.
【答案】(1)6﹣t,2t,8﹣2t(0<t<4)或2t﹣8(4<t<6);
(2)当t=2或t时,以点P,Q,E,D为顶点的四边形是平行四边形.
【分析】(1)AD=6,BC=16,点E是BC的中点,得PD=6﹣AP,BE=CE=8,则QE=8﹣CQ或QE=CQ﹣8,而CQ=2t,AP=t,则PD=6﹣t;若点Q与点E重合,则2t=8,求得t=4;若点P与点D重合,则t=6,所以当0<t<4时,则QE=8﹣2t,当4<t<6时,则QE=2t﹣8,于是得到问题的答案;
(2)由PD∥QE,可知当PD=QE时,以P、Q、E、D为顶点的四边形是平行四边形,再分两种情况讨论,一是当0<t<4,且PD=QE时,则6﹣t=8﹣2t;二是当4<t<6,且PD=QE时,则6﹣t=2t﹣8,解方程求出相应的t值即可.
【解答】解:(1)∵AD=6,BC=16,点E是BC的中点,点P在AD上,点Q在BC上,
∴PD=6﹣AP,BE=CEBC=8,
∴QE=8﹣CQ或QE=CQ﹣8,
∵点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动,
∴AP=t,
∴PD=6﹣t;
∵点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,
∴CQ=2t,
若点Q与点E重合,则2t=8,
解得t=4;
若点P与点D重合,则t=6,
当0<t<4时,则QE=8﹣2t,
当4<t<6时,则QE=2t﹣8,
故答案为:6﹣t,2t,8﹣2t或2t﹣8.
(2)∵AD∥BC,点E是BC的中点,点P在AD上,点Q在BC上,
∴PD∥QE,
∴当PD=QE时,以P、Q、E、D为顶点的四边形是平行四边形,
当0<t<4,且PD=QE时,则6﹣t=8﹣2t,
解得t=2;
当4<t<6,且PD=QE时,则6﹣t=2t﹣8,
解得t,
综上所述,当t=2或t时,以点P,Q,E,D为顶点的四边形是平行四边形.
【点评】此题重点考查一元一次方程的应用、平行四边形的判定、分类讨论数学思想的运用等知识与方法,正确地用代数式表示线段的长度是解题的关键.
15.(2024秋 沙坪坝区校级期末)如图,在平行四边形ABCD中,AC与BD相交于点O,延长CD至点E,使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AC平分∠BAE,AC=8,AE=6,求△ACE的面积.
【考点】平行四边形的判定与性质;角平分线的性质.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】(1)证明见解答;
(2)△ACE的面积是8.
【分析】(1)由平行四边形的性质得AB∥CD,AB=CD,因为延长CD至点E,使CD=DE,所以AB∥DE,AB=DE,则四边形ABDE是平行四边形;
(2)连接OE,由 ABCD的对角线AC与BD相交于点O,得OA=OCAC=4,由AC平分∠BAE,得∠BAC=∠EAC,由AB∥CD,得∠BAC=∠ECA,则∠EAC=∠ECA,所以AE=CE=6,则OE⊥AC,所以∠AOE=90°,求得OE2,则S△ACEAC OE=8.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵延长CD至点E,使CD=DE,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(2)解:连接OE,
∵ ABCD的对角线AC与BD相交于点O,AC=8,
∴OA=OCAC=4,
∵AC平分∠BAE,
∴∠BAC=∠EAC,
∵AB∥CD,
∴∠BAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=CE=6,
∴OE⊥AC,
∴∠AOE=90°,
∴OE2,
∴S△ACEAC OE8×28,
∴△ACE的面积是8.
【点评】此题重点考查平行四边形的判定与性质、等腰三角形的判定与性质、勾股定理等知识,正确地作出辅助线是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 长春校级期末)如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=CD B.AD=BC
C.AB=BC D.∠B+∠C=180°
2.(2024秋 长春校级期末)如图,在 ABCD中,∠ADC的平分线DE交BC于点E,若AB=11,BE=4,则AD的长为( )
A.15 B.11 C.20 D.52
3.(2025 山东模拟)如图,在平行四边形ABCD中,点M为边AD上一点,AM=2DM,BM平分∠ABC,点E,F分别是BM,CM的中点,若EF=3cm,则AB的长为( )
A.5.5cm B.5cm C.4.5cm D.4cm
4.(2024秋 丽水期末)如图,在 ABCD中,AB=4,BC=6,∠B=45°,E是BC边上的动点,连结DE,过点A作AF⊥DE于点F.则DE AF的值是( )
A. B. C.12 D.6
5.(2024秋 钢城区期末)如图,小华注意到跷跷板静止状态时,可以与地面构成一个△ABC,跷跷板中间的支撑杆EF垂直于地面(E、F分别为AB、AC的中点),若EF=35cm,则点B距离地面的高度为( )
A.80cm B.70cm C.60cm D.50cm
二.填空题(共5小题)
6.(2024秋 建湖县期末)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=30cm,当跷跷板的一端A着地时,另一端B离地面的高度为 cm.
7.(2024秋 重庆期末)如图,在 ABCD中,∠ABC=60°,AB=AC,对角线AC,BD交于点O,点M是CD的中点,OM=1,则△ABCD的周长为 .
8.(2024秋 西山区校级期末)如图,若平行四边形ABCD的周长为22cm,AC,BD相交于点O且BD为5cm,则△ABD的周长为 .
9.(2024秋 潍坊期末)如图, ABCD中,AD=5cm,CD=3cm,AE平分∠BAD,则EC= .
10.(2024秋 鲤城区校级期末)如图,在 ABCD中,对角线AC,BD交于点O,AC⊥CD,过点O作OE⊥AC交AD于点E,连接CE.已知AC=6,BD=10,则△CDE的周长是 .
三.解答题(共5小题)
11.(2024秋 长春校级期末)四边形ABCD中,DE⊥AC,BF⊥AC,且DE=BF,AF=CE.
(1)求证:四边形ABCD是平行四边形;
(2)若DE=4,CF=3,EF=5,则四边形ABCD的面积为 .
12.(2024秋 厦门期末)如图,四边形ABCD是平行四边形,AE⊥BC且交CB的延长线于点E,DF⊥BC于点F.证明BE=CF.
13.(2024秋 紫金县期末)如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,BD=DE=2,求四边形BEDF的面积.
14.(2024秋 钢城区期末)如图,在四边形ABCD中,AD=6,BC=16,AD∥BC,AB=8,∠ABC=60°,点E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.设运动时间为t秒.
(1)线段PD= ;CQ= ;QE= (用含t的代数式表示);
(2)当t为何值时,以点P,Q,E,D为顶点的四边形是平行四边形?
15.(2024秋 沙坪坝区校级期末)如图,在平行四边形ABCD中,AC与BD相交于点O,延长CD至点E,使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AC平分∠BAE,AC=8,AE=6,求△ACE的面积.
期末专项培优 平行四边形
参考答案与试题解析
题号 1 2 3 4 5
答案 A A D A B
一.选择题(共5小题)
1.(2024秋 长春校级期末)如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=CD B.AD=BC
C.AB=BC D.∠B+∠C=180°
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【答案】A
【分析】由AB∥CD,AB=CD,根据“一组对边平行且相等的四边形是平行四边形”证明四边形ABCD是平行四边形,可判断A符合题意;由AB∥CD,AD=BC,可知四边形ABCD是平行四边形或等腰梯形,而不能判定四边形ABCD是平行四边形,可判断B不符合题意;由AB∥CD,AB=BC,不能判定四边形ABCD是平行四边形,可判断C不符合题意;由AB∥CD,得∠B+∠C=180°,可知由AB∥CD,∠B+∠C=180°,不能判定四边形ABCD是平行四边形,可判断D不符合题意,于是得到问题的答案.
【解答】解:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
故A符合题意;
∵AB∥CD,AD=BC,
∴四边形ABCD是平行四边形或等腰梯形,
∴不能判定四边形ABCD是平行四边形,
故B不符合题意;
∵由AB∥CD,AB=BC,不能推导出AB=CD,
∴不能判定四边形ABCD是平行四边形,
故C不符合题意;
∵AB∥CD,
∴∠B+∠C=180°,
∴由AB∥CD,∠B+∠C=180°,不能判定四边形ABCD是平行四边形,
故D不符合题意,
故选:A.
【点评】此题重点考查平行四边形的判定,正确理解和运用平行四边形的判定定理是解题的关键.
2.(2024秋 长春校级期末)如图,在 ABCD中,∠ADC的平分线DE交BC于点E,若AB=11,BE=4,则AD的长为( )
A.15 B.11 C.20 D.52
【考点】平行四边形的性质;角平分线的定义;等腰三角形的判定.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】A
【分析】由∠ADC的平分线DE交BC于点E,得∠ADE=∠CDE,由平行四边形的性质得CD=AB=11,AD∥BC,则∠ADE=∠CED,所以∠CDE=∠CED,则CE=CD=11,求得AD=CB=CE+BE=15,于是得到问题的答案.
【解答】解:∵∠ADC的平分线DE交BC于点E,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,AB=11,
∴CD=AB=11,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD=11,
∵BE=4,
∴AD=CB=CE+BE=11+4=15,
故选:A.
【点评】此题重点考查角平分线的定义、平行四边形的性质、等腰三角形的判定等知识,推导出∠CDE=∠CED是解题的关键.
3.(2025 山东模拟)如图,在平行四边形ABCD中,点M为边AD上一点,AM=2DM,BM平分∠ABC,点E,F分别是BM,CM的中点,若EF=3cm,则AB的长为( )
A.5.5cm B.5cm C.4.5cm D.4cm
【考点】平行四边形的性质;三角形中位线定理.
【专题】多边形与平行四边形;推理能力.
【答案】D
【分析】根据三角形中位线定理和平行四边形的性质即可得到结论.
【解答】解:∵点E,点F分别是BM,CM中点,
∴EF是△BCM的中位线,
∵EF=3cm,
∴BC=2EF=6cm,
∵四边形ABCD是平行四边形,
∴AD=BC=6cm,
∵AD∥BC,
∴∠AMB=∠MBC,
∵BM平分∠ABC,
∴∠ABM=∠MBC,
∴∠AMB=∠ABM,
∴AM=AB,
∵AM=2MD,
∴AM=ABAD=4cm,
故选:D.
【点评】本题考查了平行四边形的性质,三角形中位线定理,熟练掌握平行四边形的性质是解题的关键.
4.(2024秋 丽水期末)如图,在 ABCD中,AB=4,BC=6,∠B=45°,E是BC边上的动点,连结DE,过点A作AF⊥DE于点F.则DE AF的值是( )
A. B. C.12 D.6
【考点】平行四边形的性质.
【专题】多边形与平行四边形;运算能力;推理能力.
【答案】A
【分析】过A作AH⊥BC于H,由等腰直角三角形的性质求出AHAB=2,由平行四边形的性质推出AD∥BC,AD=BC=6,由三角形面积公式得到DE AF=AD AH=12.
【解答】解:过A作AH⊥BC于H,
∵∠B=45°,
∴△ABH是等腰直角三角形,
∴AHAB4=2,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6,
∵AF⊥DE,
∴△EAD的面积AD AHDE AF,
∴DE AF=6×212.
故选:A.
【点评】本题考查平行四边形的性质,三角形的面积,关键是由三角形面积公式得到AD AH=DE AF.
5.(2024秋 钢城区期末)如图,小华注意到跷跷板静止状态时,可以与地面构成一个△ABC,跷跷板中间的支撑杆EF垂直于地面(E、F分别为AB、AC的中点),若EF=35cm,则点B距离地面的高度为( )
A.80cm B.70cm C.60cm D.50cm
【考点】三角形中位线定理.
【专题】三角形;推理能力.
【答案】B
【分析】根据三角形中位线定理即可解决问题.
【解答】解:∵E、F分别为AB、AC的中点,EF=35cm,
∴BC=2EF=70(cm),
∴点B距离地面的高度为70cm.
故选:B.
【点评】本题考查三角形中位线定理,解决本题的关键是掌握三角形的中位线平行于第三边并且等于第三边的一半.
二.填空题(共5小题)
6.(2024秋 建湖县期末)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=30cm,当跷跷板的一端A着地时,另一端B离地面的高度为 60 cm.
【考点】三角形中位线定理.
【专题】三角形;推理能力;应用意识.
【答案】60.
【分析】判断出OM是△ABE的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BE=2OM.
【解答】解:∵O是AB的中点,OM垂直于地面,BE垂直于地面,
∴OM∥BE,
∴OM是△ABE的中位线,
∴BE=2OM=2×30=60(cm),
另一端B离地面的高度为60cm,
故答案为:60.
【点评】本题考查了三角形中位线定理,熟记定理是解题的关键.
7.(2024秋 重庆期末)如图,在 ABCD中,∠ABC=60°,AB=AC,对角线AC,BD交于点O,点M是CD的中点,OM=1,则△ABCD的周长为 8 .
【考点】平行四边形的性质;等腰三角形的性质;等边三角形的性质;三角形中位线定理.
【专题】多边形与平行四边形;推理能力.
【答案】8.
【分析】根据平行四边形的性质得出OB=OD,进而利用三角形中位线定理得出BC=2OM,进而利用等边三角形的性质解答即可.
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD,AB=CD,OB=OD,
∵点M是CD的中点,
∴OM是△DBC的中位线,
∴BC=2OM=2,
∵∠ABC=60°,AB=AC,
∴△ABC是等边三角形,
∴AB=AC=BC=2,
∴ ABCD的周长=2×4=8,
故答案为:8.
【点评】此题考查平行四边形的性质,关键是根据平行四边形的性质得出OB=OD解答.
8.(2024秋 西山区校级期末)如图,若平行四边形ABCD的周长为22cm,AC,BD相交于点O且BD为5cm,则△ABD的周长为 16cm .
【考点】平行四边形的性质.
【专题】多边形与平行四边形;几何直观;推理能力.
【答案】16cm.
【分析】根据平行四边形的性质得到AD=BC,CD=AB,求出AD+AB=11cm,再结合BD=5cm即可解答.
【解答】解:∵平行四边形ABCD的周长为22cm,
∴AD=BC,CD=AB,AD+AB+BC+CD=22cm,
∴AD+AB=11cm,
∵AC,BD相交于点O且BD为5cm,
∴△ABD的周长为:AD+AB+BD=11+5=16(cm),
故答案为:16cm.
【点评】本题考查了平行四边形的性质,解答本题的关键是熟练掌握平行四边形的对边相等.
9.(2024秋 潍坊期末)如图, ABCD中,AD=5cm,CD=3cm,AE平分∠BAD,则EC= 2cm .
【考点】平行四边形的性质;角平分线的定义;平行线的性质;等腰三角形的判定.
【专题】多边形与平行四边形;推理能力.
【答案】2cm.
【分析】根据平行四边形的性质证明∠BAE=BAE,得BE=AB=3cm,然后根据线段的和差即可解决问题.
【解答】解:在 ABCD中,BC=AD=5cm,AB=CD=3cm,AD∥BC,
∵AE平分∠BAD,
∴∠BAE=DAE,
∵AD∥BC,
∴∠BEA=DAE,
∴∠BAE=BAE,
∴BE=AB=3cm,
∴CE=BC﹣BE=5﹣3=2(cm),
故答案为:2cm.
【点评】本题考查平行四边形的性质,角平分线定义,平行线的性质,等腰三角形的判定,解决本题的关键是得到BE=AB.
10.(2024秋 鲤城区校级期末)如图,在 ABCD中,对角线AC,BD交于点O,AC⊥CD,过点O作OE⊥AC交AD于点E,连接CE.已知AC=6,BD=10,则△CDE的周长是 4+2 .
【考点】平行四边形的性质;线段垂直平分线的性质.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】4+2.
【分析】由平行四边形的性质得OC=OAAC=3,OD=OBBD=5,而AC⊥CD,OE⊥AC,则∠ACD=90°,AE=CE,所以CD4,则AD2,再证明∠ECD=∠EDC,所以DE=CE=AEAD,即可求得△CDE的周长为4+2,于是得到问题的答案.
【解答】解:∵四边ABCD是平行四边形,对角线AC、BD交于点O,AC=6,BD=10,
∴OC=OAAC=3,OD=OBBD=5,
∵AC⊥CD,OE⊥AC,
∴∠ACD=90°,AE=CE,
∴CD4,
∴AD2,
∵∠ECD+∠ECA=90°,∠EDC+∠EAC=90°,∠ECA=∠EAC,
∴∠ECD=∠EDC,
∴DE=CE=AEAD,
∴△CDE的周长=CD+DE+CE=44+2,
∴故答案为:4+2.
【点评】此题重点考查平行四边形的性质、线段的垂直平分线的性质、等角的余角相等、勾股定理等知识,证明DE=CE=AE是解题的关键.
三.解答题(共5小题)
11.(2024秋 长春校级期末)四边形ABCD中,DE⊥AC,BF⊥AC,且DE=BF,AF=CE.
(1)求证:四边形ABCD是平行四边形;
(2)若DE=4,CF=3,EF=5,则四边形ABCD的面积为 44 .
【考点】平行四边形的判定与性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】(1)见解析;
(2)44.
【分析】(1)证△ABF≌△CDE(SAS),得AB=CD,∠BAF=∠DCE,再证AB∥CD,然后由平行四边形的判定即可得出结论;
(2)根据全等三角形的性质和三角形的面积公式即可得出结论.
【解答】(1)证明:∵DE⊥AC,BF⊥AC,
∴∠CED=∠AFB=90°,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS),
∴AB=CD,∠BAF=∠DCE,
∴AB∥CD,
∴四边形ABCD是平行四边形;
(2)解:∵CF=3,EF=5,
∴AC=AE+EF+CF=11,
∵DE⊥AC,BF⊥AC,
∴四边形ABCD的面积=2S△ABC=211×4=44,
故答案为:44.
【点评】本题考查了平行四边形的判定与性质、全等三角形的判定与性质以及勾股定理等知识,熟练掌握平行四边形的判定与性质,证明三角形全等是解题的关键.
12.(2024秋 厦门期末)如图,四边形ABCD是平行四边形,AE⊥BC且交CB的延长线于点E,DF⊥BC于点F.证明BE=CF.
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】证明见解答.
【分析】由平行四边形的性质得AB∥DC,AB=DC,则∠ABE=∠C,而∠E=∠DFC=90°,即可根据“AAS“证明△ABE≌△DCF,则BE=CF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠ABE=∠C,
∵AE⊥BC且交CB的延长线于点E,DF⊥BC于点F,
∴∠E=∠DFC=90°,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴BE=CF.
【点评】此题重点考查平行四边形的性质、全等三角形的判定与性质等知识,证明△ABE≌△DCF是解题的关键.
13.(2024秋 紫金县期末)如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,BD=DE=2,求四边形BEDF的面积.
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】多边形与平行四边形;推理能力.
【答案】(1)见解答;
(2)2.
【分析】(1)根据“SAS”及平行四边形的性质证明;
(2)根据勾股定理及平行四边形的判定和性质求解.
【解答】(1)证明:在 ABCD中,有AD=BC,AB=CD,∠A=∠C,
∵E,F分别为边AB,CD的中点,
∴AEAB,CFCD,
∴AE=CF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)解:∵∠ADB=90°,E,为边AB的中点,
∴DEAB=2,
∴AB=4,
∴AD2,
∴S△ABDAD DB=2,
∴S△BDE,
在 ABCD中,有AB=CD,AB∥CD,
∵E,F分别为边AB,CD的中点,
∴AEAB,CFCD,
∴AE=CF,
∴四边形BEDF为平行四边形,
∴S BEDF=2S△BDE=2.
【点评】本题考查了平行四边形的性质,掌握平行四边形的性质及全等三角形的判定和性质是解题的关键.
14.(2024秋 钢城区期末)如图,在四边形ABCD中,AD=6,BC=16,AD∥BC,AB=8,∠ABC=60°,点E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.设运动时间为t秒.
(1)线段PD= 6﹣t ;CQ= 2t ;QE= 8﹣2t(0<t<4)或2t﹣8(4<t<6) (用含t的代数式表示);
(2)当t为何值时,以点P,Q,E,D为顶点的四边形是平行四边形?
【考点】平行四边形的判定;列代数式.
【专题】行程问题;整式;多边形与平行四边形;运算能力;推理能力.
【答案】(1)6﹣t,2t,8﹣2t(0<t<4)或2t﹣8(4<t<6);
(2)当t=2或t时,以点P,Q,E,D为顶点的四边形是平行四边形.
【分析】(1)AD=6,BC=16,点E是BC的中点,得PD=6﹣AP,BE=CE=8,则QE=8﹣CQ或QE=CQ﹣8,而CQ=2t,AP=t,则PD=6﹣t;若点Q与点E重合,则2t=8,求得t=4;若点P与点D重合,则t=6,所以当0<t<4时,则QE=8﹣2t,当4<t<6时,则QE=2t﹣8,于是得到问题的答案;
(2)由PD∥QE,可知当PD=QE时,以P、Q、E、D为顶点的四边形是平行四边形,再分两种情况讨论,一是当0<t<4,且PD=QE时,则6﹣t=8﹣2t;二是当4<t<6,且PD=QE时,则6﹣t=2t﹣8,解方程求出相应的t值即可.
【解答】解:(1)∵AD=6,BC=16,点E是BC的中点,点P在AD上,点Q在BC上,
∴PD=6﹣AP,BE=CEBC=8,
∴QE=8﹣CQ或QE=CQ﹣8,
∵点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动,
∴AP=t,
∴PD=6﹣t;
∵点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,
∴CQ=2t,
若点Q与点E重合,则2t=8,
解得t=4;
若点P与点D重合,则t=6,
当0<t<4时,则QE=8﹣2t,
当4<t<6时,则QE=2t﹣8,
故答案为:6﹣t,2t,8﹣2t或2t﹣8.
(2)∵AD∥BC,点E是BC的中点,点P在AD上,点Q在BC上,
∴PD∥QE,
∴当PD=QE时,以P、Q、E、D为顶点的四边形是平行四边形,
当0<t<4,且PD=QE时,则6﹣t=8﹣2t,
解得t=2;
当4<t<6,且PD=QE时,则6﹣t=2t﹣8,
解得t,
综上所述,当t=2或t时,以点P,Q,E,D为顶点的四边形是平行四边形.
【点评】此题重点考查一元一次方程的应用、平行四边形的判定、分类讨论数学思想的运用等知识与方法,正确地用代数式表示线段的长度是解题的关键.
15.(2024秋 沙坪坝区校级期末)如图,在平行四边形ABCD中,AC与BD相交于点O,延长CD至点E,使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AC平分∠BAE,AC=8,AE=6,求△ACE的面积.
【考点】平行四边形的判定与性质;角平分线的性质.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】(1)证明见解答;
(2)△ACE的面积是8.
【分析】(1)由平行四边形的性质得AB∥CD,AB=CD,因为延长CD至点E,使CD=DE,所以AB∥DE,AB=DE,则四边形ABDE是平行四边形;
(2)连接OE,由 ABCD的对角线AC与BD相交于点O,得OA=OCAC=4,由AC平分∠BAE,得∠BAC=∠EAC,由AB∥CD,得∠BAC=∠ECA,则∠EAC=∠ECA,所以AE=CE=6,则OE⊥AC,所以∠AOE=90°,求得OE2,则S△ACEAC OE=8.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵延长CD至点E,使CD=DE,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(2)解:连接OE,
∵ ABCD的对角线AC与BD相交于点O,AC=8,
∴OA=OCAC=4,
∵AC平分∠BAE,
∴∠BAC=∠EAC,
∵AB∥CD,
∴∠BAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=CE=6,
∴OE⊥AC,
∴∠AOE=90°,
∴OE2,
∴S△ACEAC OE8×28,
∴△ACE的面积是8.
【点评】此题重点考查平行四边形的判定与性质、等腰三角形的判定与性质、勾股定理等知识,正确地作出辅助线是解题的关键.
21世纪教育网(www.21cnjy.com)
