【期末专项培优】数据的集中趋势(含解析)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 【期末专项培优】数据的集中趋势(含解析)2024-2025学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 571.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 10:14:50 | ||
图片预览




文档简介
期末专项培优 数据的集中趋势
一.选择题(共5小题)
1.(2024秋 茂名期末)某公司员工的月工资如下表,该公司员工月工资中的众数与中位数分别是( )
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7000 4500 2000 2400 1900 1800 1800 1800 1500
A.7000,1800 B.1800,1900 C.2000,1800 D.1800,1800
2.(2024秋 南明区期末)菲尔兹奖是数学领域的国际最高奖项,每四年颁发一次,相当于数学界的诺贝尔奖,数据37,33,29,32,35,32是部分获奖者获奖时的年龄(单位:岁),则这组数据的众数是( )
A.29岁 B.32岁 C.33岁 D.35岁
3.(2024秋 高州市期末)数据0,2,4,6,4的众数是( )
A.4 B.2 C.6 D.0
4.(2024秋 兰州期末)一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为( )
A.32 B.34 C.36 D.37
5.(2024秋 郑州期末)某校举办“身边的温暖故事”主题演讲比赛,其中前三名选手的成绩统计如表.
选手 评分项目
故事内容(单位:分) 情感表达(单位:分) 演讲技巧(单位:分)
小琪 100 85 90
小清 79 100 100
小明 95 90 90
若故事内容、情感表达、演讲技巧按4:3:3的加权平均分决定冠军、亚军、季军,则冠军、亚军、季军分别是( )
A.小清、小明、小琪 B.小清、小琪、小明
C.小琪、小明、小清 D.小琪、小清、小明
二.填空题(共5小题)
6.(2024秋 茂名期末)公司对应聘者进行创新、综合知识、语言测试,三项成绩分别为72分、50分、88分.若这三项测试得分依次按5:2:1的比例确定个人的综合成绩,则该应聘者的得分为 分.
7.(2024秋 兰州期末)数据﹣2,0,1,﹣2,﹣2的平均数是 .
8.(2024秋 中卫期末)2024年4月23日是第29个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算.小芳这四项的得分依次为85,95,92,88,则她的最后得分是 分.
9.(2024秋 西安期末)如图是某校学生年龄分布情况统计图,根据统计图计算该校学生的平均年龄为 .
10.(2024秋 碑林区校级期末)某校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小明的平时、期末成绩分别为85分,95分,则小明本学期的学业成绩为 分.
三.解答题(共5小题)
11.(2024秋 锦江区校级期末)成都嘉祥外国语学校为了提高学生的“甲流病毒防范”意识,特组织了一场“防疫”知识竞赛,学校在八、九年级中分别随机抽取了50名学生的成绩(分数)进行整理分析,已知成绩(分数)x均为整数,且分为A,B,C,D,E五个等级,分别是:A:90≤x≤100,B:80≤x<90,C:70≤x<80,D:60≤x<70,E:0≤x<60.并给出了部分信息:
①八年级B等级中由低到高的10个分数为:80,80,81,85,85,85,86,86,87,87;
②两个年级学生“防疫”知识竞赛分数统计图:
③两个年级学生“防疫”知识竞赛分数样本数据的平均数、中位数、众数如下:
平均数 中位数 众数
八年级 84 a 76
九年级 84 80 74
(1)直接写出a,m的值;
(2)若分数不低于80分表示该生对“防疫”知识掌握较好,该校八年级有学生800人,九年级有学生1000人,请估计该校八、九年级所有学生中,对“防疫”知识掌握较好的学生人数.
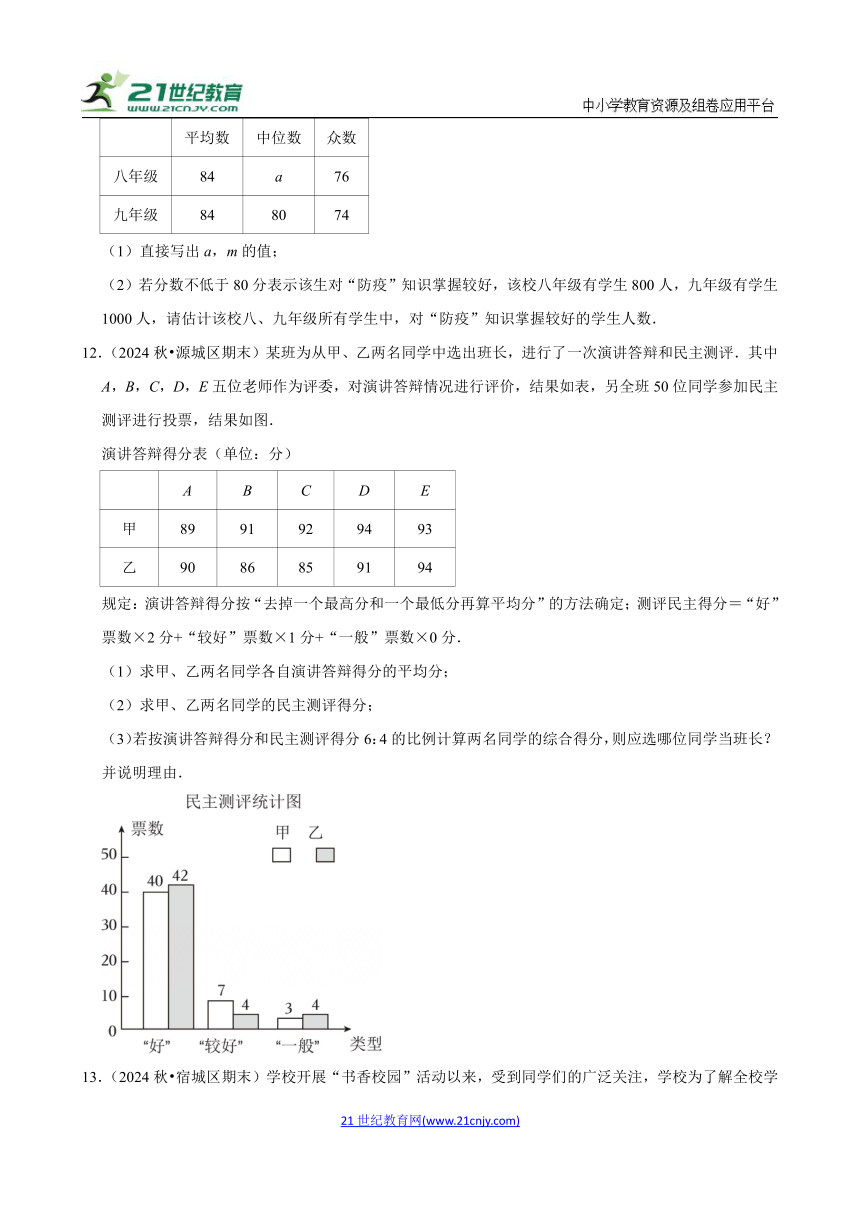
12.(2024秋 源城区期末)某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
13.(2024秋 宿城区期末)学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计表和统计图.
借阅图书的次数/次 0 1 2 3 4及以上
人数/人 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该调查统计数据的中位数是 ;
(3)若学校共有4000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
14.(2024秋 贵州期末)某校八年级(1)班50名学生参加数学质量监测考试,全班学生的成绩统计如下表:
成绩(分) 71 74 78 80 82 83 85 86 88 90 91 92 93
人数 1 2 3 5 4 5 3 7 8 4 3 3 2
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数是 ;
(2)该班学生考试成绩的中位数是 ;
(3)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中游偏上水平?试说明理由.
15.(2024秋 扬州期末)为迎接明年4月份的体育考试,九年级开展了本学期周末锻炼次数调查,便于开展后期针对性训练.现从本年级男生、女生中各抽取20名学生锻炼次数(记为x次)进行分析,将锻炼次数分为以下4组,A组:0≤x≤3;B组:4≤x≤6;C组:7≤x≤9;D组:x≥10;现将数据收集、整理、分析如下.
收集数据:男生:5,6,8,9,7,1,10,3,4,8,5,0,7,2,7,6,8,4,8,11.
女生20名学生中7≤x≤9的次数分别是:9,7,9,9,9,8,9,8.
整理分析数据:
表1:
容量等级 0≤x≤3 4≤x≤6 7≤x≤9 x≥10
男生 a 6 8 2
女生 4 5 8 3
表2:
平均数 众数 中位数
男生 5.95 b 6.5
女生 5.95 9 c
根据以上信息,解答下列问题:
(1)上述表中的a= ,b= ,c= ;
(2)通过以上数据分析,你认为男生还是女生锻炼的情况更好,请说明理由.
期末专项培优 数据的集中趋势
参考答案与试题解析
题号 1 2 3 4 5
答案 B B A C C
一.选择题(共5小题)
1.(2024秋 茂名期末)某公司员工的月工资如下表,该公司员工月工资中的众数与中位数分别是( )
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7000 4500 2000 2400 1900 1800 1800 1800 1500
A.7000,1800 B.1800,1900 C.2000,1800 D.1800,1800
【考点】众数;中位数.
【专题】常规题型.
【答案】B
【分析】根据中位数和众数的定义求解.
【解答】解:众数是一组数据中出现次数最多的数,在这一组数据中1800是出现次数最多的,故众数是1800;
而将这组数据从小到大的顺序排列后,处于中间位置的那个数是1900,那么由中位数的定义可知,这组数据的中位数是1900.
故选:B.
【点评】本题为统计题,考查众数与中位数的意义.众数是一组数据中出现次数最多的数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.
2.(2024秋 南明区期末)菲尔兹奖是数学领域的国际最高奖项,每四年颁发一次,相当于数学界的诺贝尔奖,数据37,33,29,32,35,32是部分获奖者获奖时的年龄(单位:岁),则这组数据的众数是( )
A.29岁 B.32岁 C.33岁 D.35岁
【考点】众数.
【专题】统计的应用;数据分析观念.
【答案】B
【分析】根据众数的定义求解即可.
【解答】解:∵32出现了2次,出现的次数最多,
∴这组数据的众数是32.
故选:B.
【点评】此题考查了众数,众数是一组数据中出现次数最多的数.
3.(2024秋 高州市期末)数据0,2,4,6,4的众数是( )
A.4 B.2 C.6 D.0
【考点】众数.
【专题】数据的收集与整理;数据分析观念.
【答案】A
【分析】根据众数的定义:一组数据中出现次数最多的数据即可得出答案.
【解答】解:因为数据0,2,4,6,4中4出现的次数最多,
所以数据0,2,4,6,4的众数是4.
故选:A.
【点评】本题考查了众数的知识,属于基础题,解答本题的关键是熟练掌握一组数据中出现次数最多的数据叫做众数.
4.(2024秋 兰州期末)一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为( )
A.32 B.34 C.36 D.37
【考点】中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】根据中位数的定义求解即可.
【解答】解:先对这组数据按从小到大的顺序重新排序:28,32,36,37,38,
位于最中间的数是36,
∴这组数的中位数是36.
故选:C.
【点评】本题主要考查了求一组数据的中位数,熟知中位数的定义是解题的关键:一组数据中,处在最中间的数据或处在最中间的两个数据的平均数叫做这组数据的中位数.
5.(2024秋 郑州期末)某校举办“身边的温暖故事”主题演讲比赛,其中前三名选手的成绩统计如表.
选手 评分项目
故事内容(单位:分) 情感表达(单位:分) 演讲技巧(单位:分)
小琪 100 85 90
小清 79 100 100
小明 95 90 90
若故事内容、情感表达、演讲技巧按4:3:3的加权平均分决定冠军、亚军、季军,则冠军、亚军、季军分别是( )
A.小清、小明、小琪 B.小清、小琪、小明
C.小琪、小明、小清 D.小琪、小清、小明
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】C
【分析】根据加权平均数的定义分别计算出三人的平均成绩,再比较大小即可得出答案.
【解答】解:小琪的平均成绩为92.5(分),
小清的平均成绩为91.6(分),
小明的平均成绩为92(分),
92.5>92>91.6,
所以冠军、亚军、季军分别是小琪、小明、小清.
故选:C.
【点评】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
二.填空题(共5小题)
6.(2024秋 茂名期末)公司对应聘者进行创新、综合知识、语言测试,三项成绩分别为72分、50分、88分.若这三项测试得分依次按5:2:1的比例确定个人的综合成绩,则该应聘者的得分为 68.5 分.
【考点】加权平均数.
【专题】统计的应用;数据分析观念.
【答案】68.5.
【分析】把各项成绩分别乘以其权,再除以权的和,即可求出加权平均数.
【解答】解:(分),
故答案为:68.5.
【点评】本题考查了加权平均数,熟练掌握定义是解题的关键.
7.(2024秋 兰州期末)数据﹣2,0,1,﹣2,﹣2的平均数是 ﹣1 .
【考点】算术平均数.
【专题】统计的应用;数据分析观念.
【答案】﹣1.
【分析】将题目中的数据相加,然后除以5,即可得到这组数据的平均数.
【解答】解:(﹣2+0+1﹣2﹣2)÷5
=(﹣5)÷5
=﹣1,
∴数据﹣2,0,1,﹣2,﹣2的平均数是﹣1,
故答案为:﹣1.
【点评】本题考查算术平均数,解答本题的关键是明确算术平均数的计算方法.
8.(2024秋 中卫期末)2024年4月23日是第29个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算.小芳这四项的得分依次为85,95,92,88,则她的最后得分是 90 分.
【考点】加权平均数.
【专题】运算能力.
【答案】90.
【分析】根据加权平均数的定义列式计算可得.
【解答】解:她的最后得分是85×40%+95×40%+92×10%+88×10%=90(分),
故答案为:90.
【点评】本题考查的是加权平均数的求法,熟练掌握加权平均数的计算公式是解题的关键.
9.(2024秋 西安期末)如图是某校学生年龄分布情况统计图,根据统计图计算该校学生的平均年龄为 13.95岁 .
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】见试题解答内容
【分析】根据加权平均数的计算公式列出算式,再进行计算即可得出答案.
【解答】解:根据题意得:
12×15%+13×20%+14×30%+15×25%+16×10%=13.95(岁),
答:该校学生的平均年龄为13.95岁.
故答案为:13.95岁.
【点评】此题考查了加权平均数,熟练掌握加权平均数的计算公式是解题的关键.
10.(2024秋 碑林区校级期末)某校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小明的平时、期末成绩分别为85分,95分,则小明本学期的学业成绩为 91 分.
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】91.
【分析】根据加权平均数的计算方法计算即可.
【解答】解:小明本学期的学业成绩为:85×40%+95×60%=34+57=91(分).
故答案为:91.
【点评】本题主要考查加权平均数,熟练掌握加权平均数的计算方法是解题的关键.
三.解答题(共5小题)
11.(2024秋 锦江区校级期末)成都嘉祥外国语学校为了提高学生的“甲流病毒防范”意识,特组织了一场“防疫”知识竞赛,学校在八、九年级中分别随机抽取了50名学生的成绩(分数)进行整理分析,已知成绩(分数)x均为整数,且分为A,B,C,D,E五个等级,分别是:A:90≤x≤100,B:80≤x<90,C:70≤x<80,D:60≤x<70,E:0≤x<60.并给出了部分信息:
①八年级B等级中由低到高的10个分数为:80,80,81,85,85,85,86,86,87,87;
②两个年级学生“防疫”知识竞赛分数统计图:
③两个年级学生“防疫”知识竞赛分数样本数据的平均数、中位数、众数如下:
平均数 中位数 众数
八年级 84 a 76
九年级 84 80 74
(1)直接写出a,m的值;
(2)若分数不低于80分表示该生对“防疫”知识掌握较好,该校八年级有学生800人,九年级有学生1000人,请估计该校八、九年级所有学生中,对“防疫”知识掌握较好的学生人数.
【考点】众数;用样本估计总体;加权平均数;中位数.
【专题】统计的应用;运算能力.
【答案】(1)a=83,m=30;
(2)968人.
【分析】(1)根据中位数的定义可求出中位数,根据各组频率之和等于100%,即可求出m的值;
(2)求出样本中,八年级、九年级学生分数不低于80分的所占的百分比,估计总体中分数不低于80分的所占的百分比,进而求出相应的人数.
【解答】解:(1)将八年级这50名学生的成绩从小到大排列,处在第25、26位的两个数的平均数是83,
即因此中位数是83,即a=83,
1﹣22%﹣36%﹣6%﹣6%=30%,即m=30,
答:a=83,m=30;
(2)8001000×(22%+30%)=448+520=968(人),
答:估计该校八、九年级所有学生中,对“防疫”知识掌握较好的学生人数有968人.
【点评】本题考查用样本估计总体、条形统计图、中位数、平均数,解答本题的关键是明确题意,利用数形结合的思想解答.
12.(2024秋 源城区期末)某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
【考点】加权平均数.
【专题】数据的收集与整理;应用意识.
【答案】(1)甲演讲答辩平均分为92分,乙演讲答辩平均分为89分;
(2)甲民主测评得分为87分,乙民主测评得分为88分.
(3)应选甲同学当班长.
【分析】(1)每个选手去掉一个最高分,再去掉一个最低分,求出剩下三个数的平均数即可;
(2)分别求出甲乙的民主测评得分即可.
(3)根据加权平均数的公式,计算即可判断.
【解答】解:(1)甲演讲答辩平均分92(分),
乙演讲答辩平均分:89(分),
(2)甲民主测评得分:40×2+7×1=87(分),
乙民主测评得分,42×2+4×1=88(分).
(4)甲综合得分90(分),
乙综合得分88.6(分),
∵90>88.6,
∴应选甲同学当班长.
【点评】本题考查了平均数和加权平均数的概念及应用,以及从统计图中获取信息的能力.解题的关键是理解题意,理解“权”对平均数的影响.
13.(2024秋 宿城区期末)学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计表和统计图.
借阅图书的次数/次 0 1 2 3 4及以上
人数/人 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
(1)a= 17 ,b= 20 ;
(2)该调查统计数据的中位数是 2次 ;
(3)若学校共有4000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
【考点】中位数;用样本估计总体.
【专题】统计的应用;数据分析观念.
【答案】(1)17,20;
(2)2次;
(3)240人.
【分析】(1)先求出被调查的总人数,再根据各次数的人数和等于总人数求出a的值,由百分比的概念可得b的值;
(2)根据中位数的概念求解可得;
(3)利用样本估计总体思想求解可得.
【解答】解:(1)本次调查的总人数为13÷26%=50,
∴a=50﹣(7+13+10+3)=17,
b%100%=20%,即b=20,
故答案为:17,20;
(2)该调查统计数据的中位数是2(次),
故答案为:2次;
(3)4000240(人).
答:估计该校学生在一周内借阅图书“4次及以上”的人数为240人.
【点评】本题主要考查中位数,样本估计总体.解题的关键是读懂统计图,从扇形统计图中得到必要的信息是解决问题的关键.
14.(2024秋 贵州期末)某校八年级(1)班50名学生参加数学质量监测考试,全班学生的成绩统计如下表:
成绩(分) 71 74 78 80 82 83 85 86 88 90 91 92 93
人数 1 2 3 5 4 5 3 7 8 4 3 3 2
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数是 88 ;
(2)该班学生考试成绩的中位数是 86 ;
(3)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中游偏上水平?试说明理由.
【考点】众数;中位数.
【专题】统计的应用;运算能力.
【答案】(1)88;
(2)86;
(3)不能说张华同学的成绩处于全班中游偏上水平,理由见解析.
【分析】(1)众数是指一组数据中出现次数最多的数据,据此可得到答案;
(2)将该班学生考试成绩按照从小到大的顺序排列,可得该班学生考试成绩的中位数是第25,26个数据的平均数,由此可得到答案;
(3)要判断张华同学成绩处于全班中游偏上水平,还是偏下水平,与中位数进行比较即可.
【解答】解:(1)88出现的次数最多,所以众数是88;
故答案为:88;
(2)排序后第25,26个数据的平均数是86,所以中位数是86;
故答案为:86;
(3)不能说张华同学的成绩处于全班中游偏上水平,
理由:因为全班成绩的中位数是86分,83分低于全班成绩的中位数,所以张华同学的成绩处于全班中游偏下水平.
【点评】主要考查了众数,中位数,注意众数是指一组数据中出现次数最多的数据,它反映了一组数据的多数水平,一组数据的众数可能不是唯一的,掌握确定众数与中位数的方法是解题的关键.
15.(2024秋 扬州期末)为迎接明年4月份的体育考试,九年级开展了本学期周末锻炼次数调查,便于开展后期针对性训练.现从本年级男生、女生中各抽取20名学生锻炼次数(记为x次)进行分析,将锻炼次数分为以下4组,A组:0≤x≤3;B组:4≤x≤6;C组:7≤x≤9;D组:x≥10;现将数据收集、整理、分析如下.
收集数据:男生:5,6,8,9,7,1,10,3,4,8,5,0,7,2,7,6,8,4,8,11.
女生20名学生中7≤x≤9的次数分别是:9,7,9,9,9,8,9,8.
整理分析数据:
表1:
容量等级 0≤x≤3 4≤x≤6 7≤x≤9 x≥10
男生 a 6 8 2
女生 4 5 8 3
表2:
平均数 众数 中位数
男生 5.95 b 6.5
女生 5.95 9 c
根据以上信息,解答下列问题:
(1)上述表中的a= 4 ,b= 8 ,c= 7.5 ;
(2)通过以上数据分析,你认为男生还是女生锻炼的情况更好,请说明理由.
【考点】众数;频数(率)分布表;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)4,8,7.5;
(2)女生锻炼的情况更好,理由为:女生的中位数、众数均比男生的高.
【分析】(1)用20减去已知各部分的人数可求出a;根据中位数、众数的定义可求出b,c;
(2)根据它们的平均数,中位数,众数比较分析,从而可以解答本题.
【解答】解:(1)由题意得:a=20﹣6﹣8﹣2=4;b=8;;
故答案为:4,8,7.5;
(2)女生锻炼的情况更好,理由如下:
∵女生的中位数、众数均比男生的高,
∴女生锻炼的情况更好.
【点评】本题考查平均数、众数、中位数,解题的关键是明确题意,理解有关概念,找出所求问题需要的条件.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 茂名期末)某公司员工的月工资如下表,该公司员工月工资中的众数与中位数分别是( )
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7000 4500 2000 2400 1900 1800 1800 1800 1500
A.7000,1800 B.1800,1900 C.2000,1800 D.1800,1800
2.(2024秋 南明区期末)菲尔兹奖是数学领域的国际最高奖项,每四年颁发一次,相当于数学界的诺贝尔奖,数据37,33,29,32,35,32是部分获奖者获奖时的年龄(单位:岁),则这组数据的众数是( )
A.29岁 B.32岁 C.33岁 D.35岁
3.(2024秋 高州市期末)数据0,2,4,6,4的众数是( )
A.4 B.2 C.6 D.0
4.(2024秋 兰州期末)一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为( )
A.32 B.34 C.36 D.37
5.(2024秋 郑州期末)某校举办“身边的温暖故事”主题演讲比赛,其中前三名选手的成绩统计如表.
选手 评分项目
故事内容(单位:分) 情感表达(单位:分) 演讲技巧(单位:分)
小琪 100 85 90
小清 79 100 100
小明 95 90 90
若故事内容、情感表达、演讲技巧按4:3:3的加权平均分决定冠军、亚军、季军,则冠军、亚军、季军分别是( )
A.小清、小明、小琪 B.小清、小琪、小明
C.小琪、小明、小清 D.小琪、小清、小明
二.填空题(共5小题)
6.(2024秋 茂名期末)公司对应聘者进行创新、综合知识、语言测试,三项成绩分别为72分、50分、88分.若这三项测试得分依次按5:2:1的比例确定个人的综合成绩,则该应聘者的得分为 分.
7.(2024秋 兰州期末)数据﹣2,0,1,﹣2,﹣2的平均数是 .
8.(2024秋 中卫期末)2024年4月23日是第29个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算.小芳这四项的得分依次为85,95,92,88,则她的最后得分是 分.
9.(2024秋 西安期末)如图是某校学生年龄分布情况统计图,根据统计图计算该校学生的平均年龄为 .
10.(2024秋 碑林区校级期末)某校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小明的平时、期末成绩分别为85分,95分,则小明本学期的学业成绩为 分.
三.解答题(共5小题)
11.(2024秋 锦江区校级期末)成都嘉祥外国语学校为了提高学生的“甲流病毒防范”意识,特组织了一场“防疫”知识竞赛,学校在八、九年级中分别随机抽取了50名学生的成绩(分数)进行整理分析,已知成绩(分数)x均为整数,且分为A,B,C,D,E五个等级,分别是:A:90≤x≤100,B:80≤x<90,C:70≤x<80,D:60≤x<70,E:0≤x<60.并给出了部分信息:
①八年级B等级中由低到高的10个分数为:80,80,81,85,85,85,86,86,87,87;
②两个年级学生“防疫”知识竞赛分数统计图:
③两个年级学生“防疫”知识竞赛分数样本数据的平均数、中位数、众数如下:
平均数 中位数 众数
八年级 84 a 76
九年级 84 80 74
(1)直接写出a,m的值;
(2)若分数不低于80分表示该生对“防疫”知识掌握较好,该校八年级有学生800人,九年级有学生1000人,请估计该校八、九年级所有学生中,对“防疫”知识掌握较好的学生人数.
12.(2024秋 源城区期末)某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
13.(2024秋 宿城区期末)学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计表和统计图.
借阅图书的次数/次 0 1 2 3 4及以上
人数/人 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该调查统计数据的中位数是 ;
(3)若学校共有4000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
14.(2024秋 贵州期末)某校八年级(1)班50名学生参加数学质量监测考试,全班学生的成绩统计如下表:
成绩(分) 71 74 78 80 82 83 85 86 88 90 91 92 93
人数 1 2 3 5 4 5 3 7 8 4 3 3 2
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数是 ;
(2)该班学生考试成绩的中位数是 ;
(3)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中游偏上水平?试说明理由.
15.(2024秋 扬州期末)为迎接明年4月份的体育考试,九年级开展了本学期周末锻炼次数调查,便于开展后期针对性训练.现从本年级男生、女生中各抽取20名学生锻炼次数(记为x次)进行分析,将锻炼次数分为以下4组,A组:0≤x≤3;B组:4≤x≤6;C组:7≤x≤9;D组:x≥10;现将数据收集、整理、分析如下.
收集数据:男生:5,6,8,9,7,1,10,3,4,8,5,0,7,2,7,6,8,4,8,11.
女生20名学生中7≤x≤9的次数分别是:9,7,9,9,9,8,9,8.
整理分析数据:
表1:
容量等级 0≤x≤3 4≤x≤6 7≤x≤9 x≥10
男生 a 6 8 2
女生 4 5 8 3
表2:
平均数 众数 中位数
男生 5.95 b 6.5
女生 5.95 9 c
根据以上信息,解答下列问题:
(1)上述表中的a= ,b= ,c= ;
(2)通过以上数据分析,你认为男生还是女生锻炼的情况更好,请说明理由.
期末专项培优 数据的集中趋势
参考答案与试题解析
题号 1 2 3 4 5
答案 B B A C C
一.选择题(共5小题)
1.(2024秋 茂名期末)某公司员工的月工资如下表,该公司员工月工资中的众数与中位数分别是( )
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7000 4500 2000 2400 1900 1800 1800 1800 1500
A.7000,1800 B.1800,1900 C.2000,1800 D.1800,1800
【考点】众数;中位数.
【专题】常规题型.
【答案】B
【分析】根据中位数和众数的定义求解.
【解答】解:众数是一组数据中出现次数最多的数,在这一组数据中1800是出现次数最多的,故众数是1800;
而将这组数据从小到大的顺序排列后,处于中间位置的那个数是1900,那么由中位数的定义可知,这组数据的中位数是1900.
故选:B.
【点评】本题为统计题,考查众数与中位数的意义.众数是一组数据中出现次数最多的数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.
2.(2024秋 南明区期末)菲尔兹奖是数学领域的国际最高奖项,每四年颁发一次,相当于数学界的诺贝尔奖,数据37,33,29,32,35,32是部分获奖者获奖时的年龄(单位:岁),则这组数据的众数是( )
A.29岁 B.32岁 C.33岁 D.35岁
【考点】众数.
【专题】统计的应用;数据分析观念.
【答案】B
【分析】根据众数的定义求解即可.
【解答】解:∵32出现了2次,出现的次数最多,
∴这组数据的众数是32.
故选:B.
【点评】此题考查了众数,众数是一组数据中出现次数最多的数.
3.(2024秋 高州市期末)数据0,2,4,6,4的众数是( )
A.4 B.2 C.6 D.0
【考点】众数.
【专题】数据的收集与整理;数据分析观念.
【答案】A
【分析】根据众数的定义:一组数据中出现次数最多的数据即可得出答案.
【解答】解:因为数据0,2,4,6,4中4出现的次数最多,
所以数据0,2,4,6,4的众数是4.
故选:A.
【点评】本题考查了众数的知识,属于基础题,解答本题的关键是熟练掌握一组数据中出现次数最多的数据叫做众数.
4.(2024秋 兰州期末)一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为( )
A.32 B.34 C.36 D.37
【考点】中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】根据中位数的定义求解即可.
【解答】解:先对这组数据按从小到大的顺序重新排序:28,32,36,37,38,
位于最中间的数是36,
∴这组数的中位数是36.
故选:C.
【点评】本题主要考查了求一组数据的中位数,熟知中位数的定义是解题的关键:一组数据中,处在最中间的数据或处在最中间的两个数据的平均数叫做这组数据的中位数.
5.(2024秋 郑州期末)某校举办“身边的温暖故事”主题演讲比赛,其中前三名选手的成绩统计如表.
选手 评分项目
故事内容(单位:分) 情感表达(单位:分) 演讲技巧(单位:分)
小琪 100 85 90
小清 79 100 100
小明 95 90 90
若故事内容、情感表达、演讲技巧按4:3:3的加权平均分决定冠军、亚军、季军,则冠军、亚军、季军分别是( )
A.小清、小明、小琪 B.小清、小琪、小明
C.小琪、小明、小清 D.小琪、小清、小明
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】C
【分析】根据加权平均数的定义分别计算出三人的平均成绩,再比较大小即可得出答案.
【解答】解:小琪的平均成绩为92.5(分),
小清的平均成绩为91.6(分),
小明的平均成绩为92(分),
92.5>92>91.6,
所以冠军、亚军、季军分别是小琪、小明、小清.
故选:C.
【点评】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
二.填空题(共5小题)
6.(2024秋 茂名期末)公司对应聘者进行创新、综合知识、语言测试,三项成绩分别为72分、50分、88分.若这三项测试得分依次按5:2:1的比例确定个人的综合成绩,则该应聘者的得分为 68.5 分.
【考点】加权平均数.
【专题】统计的应用;数据分析观念.
【答案】68.5.
【分析】把各项成绩分别乘以其权,再除以权的和,即可求出加权平均数.
【解答】解:(分),
故答案为:68.5.
【点评】本题考查了加权平均数,熟练掌握定义是解题的关键.
7.(2024秋 兰州期末)数据﹣2,0,1,﹣2,﹣2的平均数是 ﹣1 .
【考点】算术平均数.
【专题】统计的应用;数据分析观念.
【答案】﹣1.
【分析】将题目中的数据相加,然后除以5,即可得到这组数据的平均数.
【解答】解:(﹣2+0+1﹣2﹣2)÷5
=(﹣5)÷5
=﹣1,
∴数据﹣2,0,1,﹣2,﹣2的平均数是﹣1,
故答案为:﹣1.
【点评】本题考查算术平均数,解答本题的关键是明确算术平均数的计算方法.
8.(2024秋 中卫期末)2024年4月23日是第29个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算.小芳这四项的得分依次为85,95,92,88,则她的最后得分是 90 分.
【考点】加权平均数.
【专题】运算能力.
【答案】90.
【分析】根据加权平均数的定义列式计算可得.
【解答】解:她的最后得分是85×40%+95×40%+92×10%+88×10%=90(分),
故答案为:90.
【点评】本题考查的是加权平均数的求法,熟练掌握加权平均数的计算公式是解题的关键.
9.(2024秋 西安期末)如图是某校学生年龄分布情况统计图,根据统计图计算该校学生的平均年龄为 13.95岁 .
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】见试题解答内容
【分析】根据加权平均数的计算公式列出算式,再进行计算即可得出答案.
【解答】解:根据题意得:
12×15%+13×20%+14×30%+15×25%+16×10%=13.95(岁),
答:该校学生的平均年龄为13.95岁.
故答案为:13.95岁.
【点评】此题考查了加权平均数,熟练掌握加权平均数的计算公式是解题的关键.
10.(2024秋 碑林区校级期末)某校规定,学生的学期学业成绩由两部分组成:平时成绩占40%,期末成绩占60%,小明的平时、期末成绩分别为85分,95分,则小明本学期的学业成绩为 91 分.
【考点】加权平均数.
【专题】统计的应用;运算能力.
【答案】91.
【分析】根据加权平均数的计算方法计算即可.
【解答】解:小明本学期的学业成绩为:85×40%+95×60%=34+57=91(分).
故答案为:91.
【点评】本题主要考查加权平均数,熟练掌握加权平均数的计算方法是解题的关键.
三.解答题(共5小题)
11.(2024秋 锦江区校级期末)成都嘉祥外国语学校为了提高学生的“甲流病毒防范”意识,特组织了一场“防疫”知识竞赛,学校在八、九年级中分别随机抽取了50名学生的成绩(分数)进行整理分析,已知成绩(分数)x均为整数,且分为A,B,C,D,E五个等级,分别是:A:90≤x≤100,B:80≤x<90,C:70≤x<80,D:60≤x<70,E:0≤x<60.并给出了部分信息:
①八年级B等级中由低到高的10个分数为:80,80,81,85,85,85,86,86,87,87;
②两个年级学生“防疫”知识竞赛分数统计图:
③两个年级学生“防疫”知识竞赛分数样本数据的平均数、中位数、众数如下:
平均数 中位数 众数
八年级 84 a 76
九年级 84 80 74
(1)直接写出a,m的值;
(2)若分数不低于80分表示该生对“防疫”知识掌握较好,该校八年级有学生800人,九年级有学生1000人,请估计该校八、九年级所有学生中,对“防疫”知识掌握较好的学生人数.
【考点】众数;用样本估计总体;加权平均数;中位数.
【专题】统计的应用;运算能力.
【答案】(1)a=83,m=30;
(2)968人.
【分析】(1)根据中位数的定义可求出中位数,根据各组频率之和等于100%,即可求出m的值;
(2)求出样本中,八年级、九年级学生分数不低于80分的所占的百分比,估计总体中分数不低于80分的所占的百分比,进而求出相应的人数.
【解答】解:(1)将八年级这50名学生的成绩从小到大排列,处在第25、26位的两个数的平均数是83,
即因此中位数是83,即a=83,
1﹣22%﹣36%﹣6%﹣6%=30%,即m=30,
答:a=83,m=30;
(2)8001000×(22%+30%)=448+520=968(人),
答:估计该校八、九年级所有学生中,对“防疫”知识掌握较好的学生人数有968人.
【点评】本题考查用样本估计总体、条形统计图、中位数、平均数,解答本题的关键是明确题意,利用数形结合的思想解答.
12.(2024秋 源城区期末)某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
【考点】加权平均数.
【专题】数据的收集与整理;应用意识.
【答案】(1)甲演讲答辩平均分为92分,乙演讲答辩平均分为89分;
(2)甲民主测评得分为87分,乙民主测评得分为88分.
(3)应选甲同学当班长.
【分析】(1)每个选手去掉一个最高分,再去掉一个最低分,求出剩下三个数的平均数即可;
(2)分别求出甲乙的民主测评得分即可.
(3)根据加权平均数的公式,计算即可判断.
【解答】解:(1)甲演讲答辩平均分92(分),
乙演讲答辩平均分:89(分),
(2)甲民主测评得分:40×2+7×1=87(分),
乙民主测评得分,42×2+4×1=88(分).
(4)甲综合得分90(分),
乙综合得分88.6(分),
∵90>88.6,
∴应选甲同学当班长.
【点评】本题考查了平均数和加权平均数的概念及应用,以及从统计图中获取信息的能力.解题的关键是理解题意,理解“权”对平均数的影响.
13.(2024秋 宿城区期末)学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计表和统计图.
借阅图书的次数/次 0 1 2 3 4及以上
人数/人 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
(1)a= 17 ,b= 20 ;
(2)该调查统计数据的中位数是 2次 ;
(3)若学校共有4000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
【考点】中位数;用样本估计总体.
【专题】统计的应用;数据分析观念.
【答案】(1)17,20;
(2)2次;
(3)240人.
【分析】(1)先求出被调查的总人数,再根据各次数的人数和等于总人数求出a的值,由百分比的概念可得b的值;
(2)根据中位数的概念求解可得;
(3)利用样本估计总体思想求解可得.
【解答】解:(1)本次调查的总人数为13÷26%=50,
∴a=50﹣(7+13+10+3)=17,
b%100%=20%,即b=20,
故答案为:17,20;
(2)该调查统计数据的中位数是2(次),
故答案为:2次;
(3)4000240(人).
答:估计该校学生在一周内借阅图书“4次及以上”的人数为240人.
【点评】本题主要考查中位数,样本估计总体.解题的关键是读懂统计图,从扇形统计图中得到必要的信息是解决问题的关键.
14.(2024秋 贵州期末)某校八年级(1)班50名学生参加数学质量监测考试,全班学生的成绩统计如下表:
成绩(分) 71 74 78 80 82 83 85 86 88 90 91 92 93
人数 1 2 3 5 4 5 3 7 8 4 3 3 2
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数是 88 ;
(2)该班学生考试成绩的中位数是 86 ;
(3)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中游偏上水平?试说明理由.
【考点】众数;中位数.
【专题】统计的应用;运算能力.
【答案】(1)88;
(2)86;
(3)不能说张华同学的成绩处于全班中游偏上水平,理由见解析.
【分析】(1)众数是指一组数据中出现次数最多的数据,据此可得到答案;
(2)将该班学生考试成绩按照从小到大的顺序排列,可得该班学生考试成绩的中位数是第25,26个数据的平均数,由此可得到答案;
(3)要判断张华同学成绩处于全班中游偏上水平,还是偏下水平,与中位数进行比较即可.
【解答】解:(1)88出现的次数最多,所以众数是88;
故答案为:88;
(2)排序后第25,26个数据的平均数是86,所以中位数是86;
故答案为:86;
(3)不能说张华同学的成绩处于全班中游偏上水平,
理由:因为全班成绩的中位数是86分,83分低于全班成绩的中位数,所以张华同学的成绩处于全班中游偏下水平.
【点评】主要考查了众数,中位数,注意众数是指一组数据中出现次数最多的数据,它反映了一组数据的多数水平,一组数据的众数可能不是唯一的,掌握确定众数与中位数的方法是解题的关键.
15.(2024秋 扬州期末)为迎接明年4月份的体育考试,九年级开展了本学期周末锻炼次数调查,便于开展后期针对性训练.现从本年级男生、女生中各抽取20名学生锻炼次数(记为x次)进行分析,将锻炼次数分为以下4组,A组:0≤x≤3;B组:4≤x≤6;C组:7≤x≤9;D组:x≥10;现将数据收集、整理、分析如下.
收集数据:男生:5,6,8,9,7,1,10,3,4,8,5,0,7,2,7,6,8,4,8,11.
女生20名学生中7≤x≤9的次数分别是:9,7,9,9,9,8,9,8.
整理分析数据:
表1:
容量等级 0≤x≤3 4≤x≤6 7≤x≤9 x≥10
男生 a 6 8 2
女生 4 5 8 3
表2:
平均数 众数 中位数
男生 5.95 b 6.5
女生 5.95 9 c
根据以上信息,解答下列问题:
(1)上述表中的a= 4 ,b= 8 ,c= 7.5 ;
(2)通过以上数据分析,你认为男生还是女生锻炼的情况更好,请说明理由.
【考点】众数;频数(率)分布表;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)4,8,7.5;
(2)女生锻炼的情况更好,理由为:女生的中位数、众数均比男生的高.
【分析】(1)用20减去已知各部分的人数可求出a;根据中位数、众数的定义可求出b,c;
(2)根据它们的平均数,中位数,众数比较分析,从而可以解答本题.
【解答】解:(1)由题意得:a=20﹣6﹣8﹣2=4;b=8;;
故答案为:4,8,7.5;
(2)女生锻炼的情况更好,理由如下:
∵女生的中位数、众数均比男生的高,
∴女生锻炼的情况更好.
【点评】本题考查平均数、众数、中位数,解题的关键是明确题意,理解有关概念,找出所求问题需要的条件.
21世纪教育网(www.21cnjy.com)
