【期末专项培优】数据分析(含解析)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 【期末专项培优】数据分析(含解析)2024-2025学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 319.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 16:22:57 | ||
图片预览




文档简介
期末专项培优 数据分析
一.选择题(共5小题)
1.(2024秋 宁夏期末)下面数据中,属于定量数据的是( )
A.在公园健身的老年人的健康状况
B.某机关单位职员的学历情况
C.今年全国粮食的总产量
D.某街道各餐馆的卫生情况
2.(2024秋 贵州期末)尊老爱幼是我们中华民族的优秀传统,为了解小区老年人的健康情况,社区工作人员设计了以下几种调查方案:
方案一:在公园随机调查100名健身的老年人的健康情况;
方案二:在医院随机调查100名老年人的健康情况;
方案三:在小区内随机调查100名老年人的健康情况.
在上述方案中,能较好且准确地得到该小区老年人健康情况的是( )
A.方案一 B.方案二
C.方案三 D.以上都不行
3.(2024秋 花溪区期末)下列数据中,属于定性数据的是( )
A.小明每周做家务的时间
B.2024年除夕夜春节年欢晚会的收视率
C.某学校老师的平均年龄
D.中学生早餐是否有喝牛奶的习惯
4.(2024秋 本溪期末)某校为了了解七年级所有班级学生喜欢阅读的情况,下列做法中比较合理的是( )
A.了解每一名学生喜欢阅读的情况
B.了解每一名女生喜欢阅读的情况
C.了解每一名男生喜欢阅读的情况
D.某一个班当中随机抽取7名男同学和7名女同学,了解他们喜欢阅读的情况
5.(2024秋 新城区校级期末)学校召开运动会,20名学生要统一购买运动鞋,需要的数据是( )
A.每名学生鞋的码数 B.一部分学生鞋的码数
C.每名学生的身高 D.每名学生喜欢的款式
二.填空题(共5小题)
6.(2024秋 茂名期末)下列数据属于定量数据的是 (填序号).
①某城市的3月份的空气质量(等级)情况;
②春节档某部电影大年初一当天的票房;
③某市图书馆了解全市中学生最喜欢的图书种类.
7.(2024秋 云岩区期末)小星利用搜索引擎查到电影《志愿军:存亡之战》国庆期间的票房为8.05亿元,这个数据是 数据.(选填“定量”或“定性”)
8.(2024秋 莱西市期末)小芸为了解同学们最感兴趣的在线学习方式,设计了如下的调查问题(选项不完整):
你最感兴趣的一种在线学习方式是( )(单选)
A.B.C.D.其他
她准备从“①在线听课,②在线讨论,③在线学习2~3小时,④用手机在线学习,⑤在线阅读”中选取三个作为该问题的备选答案,合理的选取是 .(填序号)
9.(2024秋 雁塔区校级期末)下面呈现了不同类型的数据,其中是定性数据的是 .
(1)全市所有家庭的户均存款;
(2)某街道各餐馆的卫生情况;
(3)今年全国粮食的总产量;
(4)某单位的所有职位.
10.(2024秋 历下区期中)“科学用眼,保护视力”是青少年珍爱生命的具体表现.某班50名同学的视力检查数据如表所示,其中有两个数据被墨汁遮盖了,以下关于视力的统计量中可以确定的是 (填写正确的序号).
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 3 3 6 9 12 10
①平均数
②众数
③方差
三.解答题(共5小题)
11.(2024秋 郑州期末)为深入学习贯彻2024年全国“两会”精神,培养发展新质生产力所需要的高素质人才,某校组织了以“聚焦两会热点 争做时代青年”为主题的知识竞赛,并随机抽查了八、九年级各10名学生的成绩(单位:分),进行了如下数据的整理与分析.
数据收集:
八年级10名学生的竞赛成绩分别为:85,85,90,75,90,95,80,85,70,95;
九年级10名学生的竞赛成绩分别为:80,95,80,90,85,75,95,80,90,80.
数据整理分析:
平均数 中位数 众数 方差
八年级 85 a 85 60
九年级 85 82.5 b 45
根据以上统计信息,回答下列问题:
(1)表中a= ,b= ;
(2)若该校八年级600名学生均参加了本次知识竞赛,请你估计该校八年级学生本次竞赛成绩在85分及以上的学生人数;
(3)九年级的小芬认为,在此次知识竞赛中,九年级成绩比八年级成绩好,你同意吗?请选择适当的统计量说明理由.
12.(2024秋 和平区期末)为弘扬学科素养,鼓舞和平学子以实际行动诠释和平教育勇攀高峰的信心和勇气,某校八年级共推荐了19位同学参加初赛(校级演讲比赛),初赛成绩排名前10的同学进入决赛.
(1)若初赛结束后,每位同学的分数互不相同.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学成绩的 ;(填:平均数或众数或中位数)
签号 1 2 3 4 5 6 7 8 9 10
成绩 8.5 9.1 9.2 8.6 9.3 8.8 9.6 8.9 8.7 9.7
签号 11 12 13 14 15 16 17 18 19
成绩 9.8 9.1 8.9 9.3 9.6 8.8 9 8.7 9.3
(2)若初赛结束后,这19位同学的成绩如表:2号选手笑着说:“我的成绩代表着咱们这19位同学的平均水平呀!”14号选手说:“与我同分数的选手最多,我的成绩代表着咱们这19位选手的大众水平嘛!”请问,这19位同学成绩的平均数为 ,众数为 ;
(3)已知10号选手与15号选手经常参加此类演讲比赛,她俩想看看近期谁的成绩较好、较稳定,她俩用近三次同时参加演讲比赛的成绩计算得到平均分一样,10号选手的方差为0.5,15号选手的方差为0.38.你认为 号选手的成绩比较稳定.
13.(2024 当阳市模拟)为培养学生的数学思维,激发学生学习数学的兴趣,我校某班开展了学生数学讲题比赛,分别从男同学和女同学中各选出10位选手参赛,成绩如下:
男同学:85,85,90,75,90,95,80,85,70,95;
女同学:80,95,80,90,85,75,95,80,90,80.
数据整理分析如表:
平均数 中位数 众数 方差
男同学 85 a 85 60
女同学 85 82.5 b 45
根据以上统计信息,回答下列问题:
(1)表中a= ,b= .
(2)女同学小红参加了本次讲题比赛,已知她的成绩在女同学中是中等偏上,则小红的成绩最低可能为 分.
(3)小红认为在此次讲题比赛中,女同学成绩比男同学成绩好,你同意吗?请选择适当的统计量说明理由.
14.(2024秋 保定期中)嘉琪家的猕猴桃成熟了.嘉琪的爸爸将自家猕猴桃挂在网上销售,原计划是每天卖200kg,但是实际销售受到各方面因素的影响,与原计划有出入.下表是嘉琪记录的某周销售情况(超出计划记为正,不足记为负).
星期 一 二 三 四 五 六 日
与原计划的差值/kg +8 +7 ﹣4 ﹣6 +1 +3 ﹣3
(1)根据表中的数据,这周猕猴桃一共卖了多少kg?
(2)根据表中的数据,这周猕猴桃销售最多的一天比销售最少的一天多销售了多少kg?
(3)若嘉琪家的猕猴桃以5元/kg的价格出售,嘉琪的爸爸通过计算,得出猕猴桃的成本为2元/kg,则这一周嘉琪家卖出的猕猴桃能赚多少元?
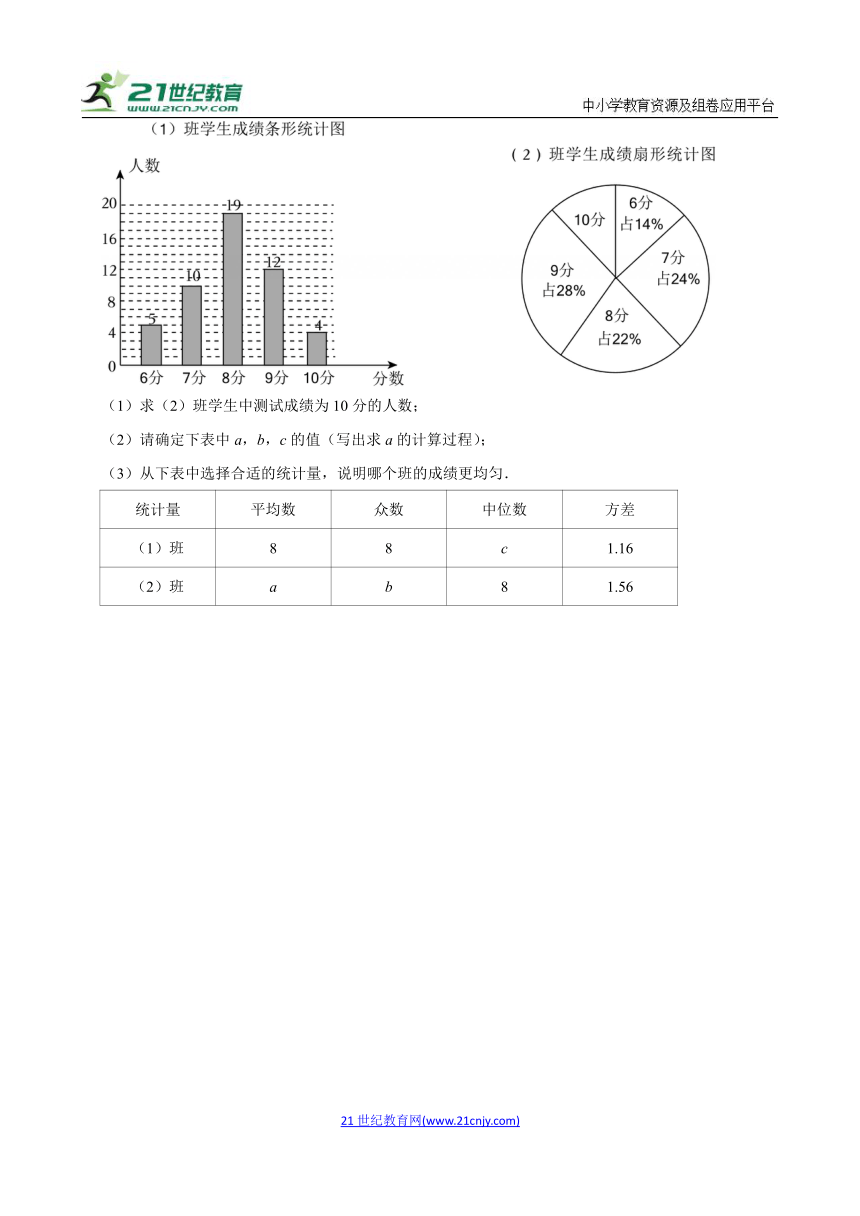
15.(2024秋 东平县期中)为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如图所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(写出求a的计算过程);
(3)从下表中选择合适的统计量,说明哪个班的成绩更均匀.
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
期末专项培优 数据分析
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 宁夏期末)下面数据中,属于定量数据的是( )
A.在公园健身的老年人的健康状况
B.某机关单位职员的学历情况
C.今年全国粮食的总产量
D.某街道各餐馆的卫生情况
【考点】调查收集数据的过程与方法.
【专题】统计与概率;应用意识.
【答案】C
【分析】通常以文字、符号或类别来表示,不具备数值意义;定量数据:也称为连续数据或数值型数据,是数值型的数据,可以进行数值计算和统计分析,据此进行判断即可.
【解答】解:A、在公园健身的老年人的健康状况,为定性数据,不符合题意;
B、某机关单位职员的学历情况,为定性数据,不符合题意;
C、今年全国粮食的总产量,为定量数据,符合题意;
D、某街道各餐馆的卫生情况,为定性数据,不符合题意.
故选:C.
【点评】本题考查定量数据和定性数据,定性数据:也称为分类数据,是非数值型的数据,描述事物的特征或属性,正确记忆相关知识点是解题关键.
2.(2024秋 贵州期末)尊老爱幼是我们中华民族的优秀传统,为了解小区老年人的健康情况,社区工作人员设计了以下几种调查方案:
方案一:在公园随机调查100名健身的老年人的健康情况;
方案二:在医院随机调查100名老年人的健康情况;
方案三:在小区内随机调查100名老年人的健康情况.
在上述方案中,能较好且准确地得到该小区老年人健康情况的是( )
A.方案一 B.方案二
C.方案三 D.以上都不行
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;统计的应用;数据分析观念.
【答案】C
【分析】根据样本的代表性进行判断即可.
【解答】解:方案一:在公园随机调查100名健身的老年人的健康情况,在公园健身的老年人身体往往都非常好,因此抽样不具有代表性,不能全面反映该小区的老年人健康状况;
方案二:在医院随机调查100名老年人的健康情况,在医院的老年人身体往往都不好,因此抽样不具有代表性,不能全面反映该小区的老年人健康状况;
方案三:在小区内随机调查100名老年人的健康情况,抽样具有代表性,因此能全面反映该小区的老年人健康状况;
故选:C.
【点评】本题考查抽样调查,理解抽样的代表性和普遍性是正确判断的关键.
3.(2024秋 花溪区期末)下列数据中,属于定性数据的是( )
A.小明每周做家务的时间
B.2024年除夕夜春节年欢晚会的收视率
C.某学校老师的平均年龄
D.中学生早餐是否有喝牛奶的习惯
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;应用意识.
【答案】D
【分析】根据定量数据与定性数据的定义解答即可.
【解答】解:A、小明每周做家务的时间是定量数据,不符合题意;
B、2024年除夕夜春节年欢晚会的收视率是定量数据,不符合题意;
C、某学校老师的平均年龄是定量数据,不符合题意;
D、中学生早餐是否有喝牛奶的习惯是定性数据,符合题意;
故选:D.
【点评】本题考查了调查收集数据的过程与方法,熟练掌握统计数据分为定量数据与定性数据以及它们的定义是解题的关键.
4.(2024秋 本溪期末)某校为了了解七年级所有班级学生喜欢阅读的情况,下列做法中比较合理的是( )
A.了解每一名学生喜欢阅读的情况
B.了解每一名女生喜欢阅读的情况
C.了解每一名男生喜欢阅读的情况
D.某一个班当中随机抽取7名男同学和7名女同学,了解他们喜欢阅读的情况
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;数据分析观念.
【答案】D
【分析】根据样本抽样的原则要求,逐项进行判断即可.
【解答】解:A.人数太多不合理,故该选项不符合题意;
B.不能反映全面的情况,不具有代表性,故该选项不符合题意;
C.不能反映全面的情况,不具有代表性,故该选项不符合题意;
D.了解他们喜欢阅读的情况比较合理,故该选项符合题意;
故选:D.
【点评】本题考查样本抽样的原则和要求,掌握样本抽样具有普遍性、代表性和可操作性,是正确判断的前提.
5.(2024秋 新城区校级期末)学校召开运动会,20名学生要统一购买运动鞋,需要的数据是( )
A.每名学生鞋的码数 B.一部分学生鞋的码数
C.每名学生的身高 D.每名学生喜欢的款式
【考点】统计量的选择.
【专题】统计与概率;数据分析观念.
【答案】A
【分析】根据数据的收集方法求解即可.
【解答】解:学校召开运动会,20名学生要统一购买运动鞋,需要的数据是每名学生鞋的码数,
故选:A.
【点评】本题考查了数据的收集与整理.熟练掌握数据的收集方法是解题的关键.
二.填空题(共5小题)
6.(2024秋 茂名期末)下列数据属于定量数据的是 ② (填序号).
①某城市的3月份的空气质量(等级)情况;
②春节档某部电影大年初一当天的票房;
③某市图书馆了解全市中学生最喜欢的图书种类.
【考点】调查收集数据的过程与方法.
【专题】统计与概率;数据分析观念.
【答案】②.
【分析】定量数据是确定数量关系的数据,定性数据是确定事务属性的数据,据此可得答案.
【解答】解:根据定量数据是确定数量关系的数据,定性数据是确定事务属性的数据可知:
①某城市的3月份的空气质量(等级)情况,是定性数据;
②春节档某部电影大年初一当天的票房,是定量数据;
③某市图书馆了解全市中学生最喜欢的图书种类,是定性数据.
故答案为:②.
【点评】本题考查了调查收集数据的过程与方法,根据定性数据的意义做出正确的判断是解题的关键.
7.(2024秋 云岩区期末)小星利用搜索引擎查到电影《志愿军:存亡之战》国庆期间的票房为8.05亿元,这个数据是 定量 数据.(选填“定量”或“定性”)
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;应用意识.
【答案】定量.
【分析】根据定量数据和定性数据的定义进行判断即可.
【解答】解:小星利用搜索引擎查到电影《志愿军:存亡之战》国庆期间的票房为8.05亿元,这个数据是定量数据.
故答案为:定量.
【点评】本题考查调查收集数据的过程与方法,掌握定量数据和定性数据的定义是正确解答的关键.
8.(2024秋 莱西市期末)小芸为了解同学们最感兴趣的在线学习方式,设计了如下的调查问题(选项不完整):
你最感兴趣的一种在线学习方式是( )(单选)
A.B.C.D.其他
她准备从“①在线听课,②在线讨论,③在线学习2~3小时,④用手机在线学习,⑤在线阅读”中选取三个作为该问题的备选答案,合理的选取是 ①②⑤ .(填序号)
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;数据分析观念.
【答案】见试题解答内容
【分析】根据题意可得“①在线听课,②在线讨论,⑤在线阅读”合理.
【解答】解:根据题意可知:
①在线听课,②在线讨论,⑤在线阅读,
作为该问题的备选答案合理,
故答案为:①②⑤.
【点评】本题考查了调查收集数据的过程与方法,解决本题的关键是掌握收集数据的过程与方法.
9.(2024秋 雁塔区校级期末)下面呈现了不同类型的数据,其中是定性数据的是 (2)(4) .
(1)全市所有家庭的户均存款;
(2)某街道各餐馆的卫生情况;
(3)今年全国粮食的总产量;
(4)某单位的所有职位.
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;应用意识.
【答案】(2)(4).
【分析】根据定量数据与定性数据的定义解答即可.
【解答】解:(1)全市所有家庭的户均存款是定量数据;
(2)某街道各餐馆的卫生情况是定性数据;
(3)今年全国粮食的总产量是定量数据;
(4)某单位的所有职位是定性数据.
故答案为:(2)(4).
【点评】本题考查了调查收集数据的过程与方法,熟练掌握统计数据分为定量数据与定性数据以及它们的定义是解题的关键.
10.(2024秋 历下区期中)“科学用眼,保护视力”是青少年珍爱生命的具体表现.某班50名同学的视力检查数据如表所示,其中有两个数据被墨汁遮盖了,以下关于视力的统计量中可以确定的是 ② (填写正确的序号).
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 3 3 6 9 12 10
①平均数
②众数
③方差
【考点】统计量的选择;加权平均数;众数;方差.
【专题】统计的应用;数据分析观念.
【答案】②.
【分析】通过计算视力为4.9、5.0的人数,进行判断,不影响视力出现次数最多的结果,因此不影响众数,同时不影响找第25、26位数据,因此不影响中位数的计算,进而进行选择.
【解答】解:由表格数据可知,成绩为4.9、5.0的人数为50﹣(3+3+6+9+12+10)=7(人),
视力为4.7出现次数最多,因此视力的众数是4.7,
视力从小到大排列后处在第25、26位的两个数都是4.7,因此中位数是4.7,
因此中位数和众数与被遮盖的数据无关,即关于视力的统计量中可以确定的是中位数和众数.
故答案为:②.
【点评】考查中位数、众数、方差、平均数的意义和计算方法,理解各个统计量的实际意义,以及每个统计量所反应数据的特征,是正确判断的前提.
三.解答题(共5小题)
11.(2024秋 郑州期末)为深入学习贯彻2024年全国“两会”精神,培养发展新质生产力所需要的高素质人才,某校组织了以“聚焦两会热点 争做时代青年”为主题的知识竞赛,并随机抽查了八、九年级各10名学生的成绩(单位:分),进行了如下数据的整理与分析.
数据收集:
八年级10名学生的竞赛成绩分别为:85,85,90,75,90,95,80,85,70,95;
九年级10名学生的竞赛成绩分别为:80,95,80,90,85,75,95,80,90,80.
数据整理分析:
平均数 中位数 众数 方差
八年级 85 a 85 60
九年级 85 82.5 b 45
根据以上统计信息,回答下列问题:
(1)表中a= 85 ,b= 80 ;
(2)若该校八年级600名学生均参加了本次知识竞赛,请你估计该校八年级学生本次竞赛成绩在85分及以上的学生人数;
(3)九年级的小芬认为,在此次知识竞赛中,九年级成绩比八年级成绩好,你同意吗?请选择适当的统计量说明理由.
【考点】统计量的选择;用样本估计总体;中位数;众数;方差.
【专题】统计的应用;数据分析观念.
【答案】(1)85,80;(2)420人;(3)同意.
【分析】(1)根据中位数、众数的定义直接求解即可;
(2)用600乘以八年级学生本次竞赛成绩在85分及以上的学生人数所占的比例即可;
(3)根据平均数、中位数、众数以及方差的意义判断即可.
【解答】解:(1)八年级10名学生的竞赛成绩排序:70,75,80,85,85,85,90,90,95,95,
∵中间的数是85,85,
∴中位数a=(85+85)÷2=85,
∵九年级10名学生的竞赛成绩中,80出现次数最多,
∴这组数据的众数是80,即b的值为80,
故答案为:85,80;
(2)600420(人),
答:估计该校八年级学生本次竞赛成绩在85分及以上的学生人数为420人;
(3)同意.
理由:∵两个年级学生竞赛成绩的平均数相同,而九年级学生竞赛成绩的方差小,成绩稳定,
∴九年级成绩比八年级成绩好.
【点评】本题考查了统计表、中位数、众数、平均数和方差,熟练掌握中位数、众数的定义,用将本估计总体等知识是解答此题的关键.
12.(2024秋 和平区期末)为弘扬学科素养,鼓舞和平学子以实际行动诠释和平教育勇攀高峰的信心和勇气,某校八年级共推荐了19位同学参加初赛(校级演讲比赛),初赛成绩排名前10的同学进入决赛.
(1)若初赛结束后,每位同学的分数互不相同.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学成绩的 中位数 ;(填:平均数或众数或中位数)
签号 1 2 3 4 5 6 7 8 9 10
成绩 8.5 9.1 9.2 8.6 9.3 8.8 9.6 8.9 8.7 9.7
签号 11 12 13 14 15 16 17 18 19
成绩 9.8 9.1 8.9 9.3 9.6 8.8 9 8.7 9.3
(2)若初赛结束后,这19位同学的成绩如表:2号选手笑着说:“我的成绩代表着咱们这19位同学的平均水平呀!”14号选手说:“与我同分数的选手最多,我的成绩代表着咱们这19位选手的大众水平嘛!”请问,这19位同学成绩的平均数为 9.1 ,众数为 9.3 ;
(3)已知10号选手与15号选手经常参加此类演讲比赛,她俩想看看近期谁的成绩较好、较稳定,她俩用近三次同时参加演讲比赛的成绩计算得到平均分一样,10号选手的方差为0.5,15号选手的方差为0.38.你认为 15 号选手的成绩比较稳定.
【考点】统计量的选择;算术平均数;中位数;众数;方差.
【专题】统计的应用;数据分析观念;运算能力.
【答案】(1)中位数;
(2)9.1,9.3;
(3)15.
【分析】(1)因为第10名同学的成绩排在中间位置,即是中位数,所以需知道这 19位同学成绩的中位数;
(2)根据平均数公式求解即可;
(3)根据方差的意义分析.
【解答】解:(1)19位同学参加演讲比赛,所得的分数互不相同,取得前10位同学进入决赛,中位数就是第10位,因而要判断自己能否进入决赛,他只需知道这19位同学的中位数就可以;
故答案为:中位数;
(2)19位同学成绩的平均数(8.5+9.1+9.2+8.6+9.3+8.8+9.6+8.9+8.7+9.7+9.8+9.1+8.9+9.3+9.6+8.8+9+8.7+9.3)=9.1,众数为9.3;
故答案为:9.1,9.3;
(3)∵她俩用近三次同时参加演讲比赛的成绩计算得到平均分一样,10号选手的方差为0.5,15号选手的方差为0.38,15号的方差小,
∴15号选手的成绩比较稳定.
故答案为:15.
【点评】本题考查了中位数,平均数,众数,方差,此题不但要求学生会求,而且要求掌握方差、平均数、众数的运用.
13.(2024 当阳市模拟)为培养学生的数学思维,激发学生学习数学的兴趣,我校某班开展了学生数学讲题比赛,分别从男同学和女同学中各选出10位选手参赛,成绩如下:
男同学:85,85,90,75,90,95,80,85,70,95;
女同学:80,95,80,90,85,75,95,80,90,80.
数据整理分析如表:
平均数 中位数 众数 方差
男同学 85 a 85 60
女同学 85 82.5 b 45
根据以上统计信息,回答下列问题:
(1)表中a= 85 ,b= 80 .
(2)女同学小红参加了本次讲题比赛,已知她的成绩在女同学中是中等偏上,则小红的成绩最低可能为 82.5 分.
(3)小红认为在此次讲题比赛中,女同学成绩比男同学成绩好,你同意吗?请选择适当的统计量说明理由.
【考点】统计量的选择;中位数;众数;方差.
【专题】统计的应用;数据分析观念.
【答案】(1)85,80;
(2)82.5;
(3)同意,理由见解析.
【分析】(1)根据中位数、众数的定义直接求解即可;
(2)根据中位数的定义判断即可;
(3)根据方差的意义解答即可.
【解答】解:(1)把男同学的成绩从小到大排列为:70,75,80,85,85,85,90,90,95,95,故中位数为a85,
女同学的成绩中80出现的次数最多,故众数b=80;
故答案为:85,80;
(2)小红参加了本次讲题比赛,已知她的成绩是中等偏上,则小红的成绩最低可能为82.5分;
故答案为:82.5;
(3)同意,理由如下:
因为女同学成绩的方差小于男同学的,成绩波动小,所以女同学的成绩更好.
【点评】本题考查了统计量的选择、中位数、众数、方差等知识,熟练掌握中位数、众数、方差的定义是解答此题的关键.
14.(2024秋 保定期中)嘉琪家的猕猴桃成熟了.嘉琪的爸爸将自家猕猴桃挂在网上销售,原计划是每天卖200kg,但是实际销售受到各方面因素的影响,与原计划有出入.下表是嘉琪记录的某周销售情况(超出计划记为正,不足记为负).
星期 一 二 三 四 五 六 日
与原计划的差值/kg +8 +7 ﹣4 ﹣6 +1 +3 ﹣3
(1)根据表中的数据,这周猕猴桃一共卖了多少kg?
(2)根据表中的数据,这周猕猴桃销售最多的一天比销售最少的一天多销售了多少kg?
(3)若嘉琪家的猕猴桃以5元/kg的价格出售,嘉琪的爸爸通过计算,得出猕猴桃的成本为2元/kg,则这一周嘉琪家卖出的猕猴桃能赚多少元?
【考点】调查收集数据的过程与方法;正数和负数.
【专题】统计与概率;数据分析观念.
【答案】(1)1406kg;
(2)14kg;
(3)4218元.
【分析】(1)用7天的计划销量加上7天的出入量即可;
(2)用表格中最大的数减去最小的数即可;
(3)用销售量乘以每千克的利润即可.
【解答】解:(1)根据表中的数据进行计算如下:
200×7+(8+7﹣4﹣6+1+3﹣3)=1400+6=1406(kg).
答:这周猕猴桃一共卖了1406kg.
(2)8﹣(﹣6)=14(kg).
答:多销售14kg.
(3)1406×(5﹣2)=1406×3=4218(元).
答:这一周嘉琪家卖出的猕猴桃能赚4218元.
【点评】本题考查了有理数混合运算的应用,根据题意列出算式是解答本题的关键.
15.(2024秋 东平县期中)为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如图所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(写出求a的计算过程);
(3)从下表中选择合适的统计量,说明哪个班的成绩更均匀.
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
【考点】统计量的选择;中位数;众数;方差.
【专题】统计的应用;应用意识.
【答案】(1)(2)班学生中测试成绩为(10分)的人数是6人
(2)a=8,b=9,c=8
(3)(1)班成绩更均匀,见解析.
【分析】(1)根据条形统计图求出两班的总人数,结合扇形统计图占比即可得到答案;
(2)根据条形统计图人数找到最中间的项及扇形统计图占比最大的即可得到b,c,利用加权平均数计算公式即可得到a,即可得到答案;
(3)根据方差的意义判断即可得到答案.
【解答】解:(1)由题意知,(1)班和(2)班人数相等,
为:5+10+19+12+4=50(人),
∴(2)班学生中测试成绩为(10分)的人数为:50×(1﹣28%﹣22%﹣24%﹣14%)=6(人),
答:(2)班学生中测试成绩为(10分)的人数是6人;
(2)由题意知,a(6×10+50×28%×9+50×22%×8+50×24%×7+50×14%×6)=8,
由题意可得扇形统计图中(9分)的人数占28%最大,条形统计图中5+10<25<26<5+10+19,
∴b=9;c=8;
答:a,b,c的值分别为8,9,8;
(3)由题意可得,
∵1.16<1.56,
∴(1)班成绩更均匀.
【点评】本题考查直方图与扇形统计图共存求解问题,求平均数,求众数,求中位数及根据方差判断稳定性,解题的关键是看懂两个图及熟练在掌握方差越小,数据分布越均匀.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 宁夏期末)下面数据中,属于定量数据的是( )
A.在公园健身的老年人的健康状况
B.某机关单位职员的学历情况
C.今年全国粮食的总产量
D.某街道各餐馆的卫生情况
2.(2024秋 贵州期末)尊老爱幼是我们中华民族的优秀传统,为了解小区老年人的健康情况,社区工作人员设计了以下几种调查方案:
方案一:在公园随机调查100名健身的老年人的健康情况;
方案二:在医院随机调查100名老年人的健康情况;
方案三:在小区内随机调查100名老年人的健康情况.
在上述方案中,能较好且准确地得到该小区老年人健康情况的是( )
A.方案一 B.方案二
C.方案三 D.以上都不行
3.(2024秋 花溪区期末)下列数据中,属于定性数据的是( )
A.小明每周做家务的时间
B.2024年除夕夜春节年欢晚会的收视率
C.某学校老师的平均年龄
D.中学生早餐是否有喝牛奶的习惯
4.(2024秋 本溪期末)某校为了了解七年级所有班级学生喜欢阅读的情况,下列做法中比较合理的是( )
A.了解每一名学生喜欢阅读的情况
B.了解每一名女生喜欢阅读的情况
C.了解每一名男生喜欢阅读的情况
D.某一个班当中随机抽取7名男同学和7名女同学,了解他们喜欢阅读的情况
5.(2024秋 新城区校级期末)学校召开运动会,20名学生要统一购买运动鞋,需要的数据是( )
A.每名学生鞋的码数 B.一部分学生鞋的码数
C.每名学生的身高 D.每名学生喜欢的款式
二.填空题(共5小题)
6.(2024秋 茂名期末)下列数据属于定量数据的是 (填序号).
①某城市的3月份的空气质量(等级)情况;
②春节档某部电影大年初一当天的票房;
③某市图书馆了解全市中学生最喜欢的图书种类.
7.(2024秋 云岩区期末)小星利用搜索引擎查到电影《志愿军:存亡之战》国庆期间的票房为8.05亿元,这个数据是 数据.(选填“定量”或“定性”)
8.(2024秋 莱西市期末)小芸为了解同学们最感兴趣的在线学习方式,设计了如下的调查问题(选项不完整):
你最感兴趣的一种在线学习方式是( )(单选)
A.B.C.D.其他
她准备从“①在线听课,②在线讨论,③在线学习2~3小时,④用手机在线学习,⑤在线阅读”中选取三个作为该问题的备选答案,合理的选取是 .(填序号)
9.(2024秋 雁塔区校级期末)下面呈现了不同类型的数据,其中是定性数据的是 .
(1)全市所有家庭的户均存款;
(2)某街道各餐馆的卫生情况;
(3)今年全国粮食的总产量;
(4)某单位的所有职位.
10.(2024秋 历下区期中)“科学用眼,保护视力”是青少年珍爱生命的具体表现.某班50名同学的视力检查数据如表所示,其中有两个数据被墨汁遮盖了,以下关于视力的统计量中可以确定的是 (填写正确的序号).
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 3 3 6 9 12 10
①平均数
②众数
③方差
三.解答题(共5小题)
11.(2024秋 郑州期末)为深入学习贯彻2024年全国“两会”精神,培养发展新质生产力所需要的高素质人才,某校组织了以“聚焦两会热点 争做时代青年”为主题的知识竞赛,并随机抽查了八、九年级各10名学生的成绩(单位:分),进行了如下数据的整理与分析.
数据收集:
八年级10名学生的竞赛成绩分别为:85,85,90,75,90,95,80,85,70,95;
九年级10名学生的竞赛成绩分别为:80,95,80,90,85,75,95,80,90,80.
数据整理分析:
平均数 中位数 众数 方差
八年级 85 a 85 60
九年级 85 82.5 b 45
根据以上统计信息,回答下列问题:
(1)表中a= ,b= ;
(2)若该校八年级600名学生均参加了本次知识竞赛,请你估计该校八年级学生本次竞赛成绩在85分及以上的学生人数;
(3)九年级的小芬认为,在此次知识竞赛中,九年级成绩比八年级成绩好,你同意吗?请选择适当的统计量说明理由.
12.(2024秋 和平区期末)为弘扬学科素养,鼓舞和平学子以实际行动诠释和平教育勇攀高峰的信心和勇气,某校八年级共推荐了19位同学参加初赛(校级演讲比赛),初赛成绩排名前10的同学进入决赛.
(1)若初赛结束后,每位同学的分数互不相同.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学成绩的 ;(填:平均数或众数或中位数)
签号 1 2 3 4 5 6 7 8 9 10
成绩 8.5 9.1 9.2 8.6 9.3 8.8 9.6 8.9 8.7 9.7
签号 11 12 13 14 15 16 17 18 19
成绩 9.8 9.1 8.9 9.3 9.6 8.8 9 8.7 9.3
(2)若初赛结束后,这19位同学的成绩如表:2号选手笑着说:“我的成绩代表着咱们这19位同学的平均水平呀!”14号选手说:“与我同分数的选手最多,我的成绩代表着咱们这19位选手的大众水平嘛!”请问,这19位同学成绩的平均数为 ,众数为 ;
(3)已知10号选手与15号选手经常参加此类演讲比赛,她俩想看看近期谁的成绩较好、较稳定,她俩用近三次同时参加演讲比赛的成绩计算得到平均分一样,10号选手的方差为0.5,15号选手的方差为0.38.你认为 号选手的成绩比较稳定.
13.(2024 当阳市模拟)为培养学生的数学思维,激发学生学习数学的兴趣,我校某班开展了学生数学讲题比赛,分别从男同学和女同学中各选出10位选手参赛,成绩如下:
男同学:85,85,90,75,90,95,80,85,70,95;
女同学:80,95,80,90,85,75,95,80,90,80.
数据整理分析如表:
平均数 中位数 众数 方差
男同学 85 a 85 60
女同学 85 82.5 b 45
根据以上统计信息,回答下列问题:
(1)表中a= ,b= .
(2)女同学小红参加了本次讲题比赛,已知她的成绩在女同学中是中等偏上,则小红的成绩最低可能为 分.
(3)小红认为在此次讲题比赛中,女同学成绩比男同学成绩好,你同意吗?请选择适当的统计量说明理由.
14.(2024秋 保定期中)嘉琪家的猕猴桃成熟了.嘉琪的爸爸将自家猕猴桃挂在网上销售,原计划是每天卖200kg,但是实际销售受到各方面因素的影响,与原计划有出入.下表是嘉琪记录的某周销售情况(超出计划记为正,不足记为负).
星期 一 二 三 四 五 六 日
与原计划的差值/kg +8 +7 ﹣4 ﹣6 +1 +3 ﹣3
(1)根据表中的数据,这周猕猴桃一共卖了多少kg?
(2)根据表中的数据,这周猕猴桃销售最多的一天比销售最少的一天多销售了多少kg?
(3)若嘉琪家的猕猴桃以5元/kg的价格出售,嘉琪的爸爸通过计算,得出猕猴桃的成本为2元/kg,则这一周嘉琪家卖出的猕猴桃能赚多少元?
15.(2024秋 东平县期中)为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如图所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(写出求a的计算过程);
(3)从下表中选择合适的统计量,说明哪个班的成绩更均匀.
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
期末专项培优 数据分析
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 宁夏期末)下面数据中,属于定量数据的是( )
A.在公园健身的老年人的健康状况
B.某机关单位职员的学历情况
C.今年全国粮食的总产量
D.某街道各餐馆的卫生情况
【考点】调查收集数据的过程与方法.
【专题】统计与概率;应用意识.
【答案】C
【分析】通常以文字、符号或类别来表示,不具备数值意义;定量数据:也称为连续数据或数值型数据,是数值型的数据,可以进行数值计算和统计分析,据此进行判断即可.
【解答】解:A、在公园健身的老年人的健康状况,为定性数据,不符合题意;
B、某机关单位职员的学历情况,为定性数据,不符合题意;
C、今年全国粮食的总产量,为定量数据,符合题意;
D、某街道各餐馆的卫生情况,为定性数据,不符合题意.
故选:C.
【点评】本题考查定量数据和定性数据,定性数据:也称为分类数据,是非数值型的数据,描述事物的特征或属性,正确记忆相关知识点是解题关键.
2.(2024秋 贵州期末)尊老爱幼是我们中华民族的优秀传统,为了解小区老年人的健康情况,社区工作人员设计了以下几种调查方案:
方案一:在公园随机调查100名健身的老年人的健康情况;
方案二:在医院随机调查100名老年人的健康情况;
方案三:在小区内随机调查100名老年人的健康情况.
在上述方案中,能较好且准确地得到该小区老年人健康情况的是( )
A.方案一 B.方案二
C.方案三 D.以上都不行
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;统计的应用;数据分析观念.
【答案】C
【分析】根据样本的代表性进行判断即可.
【解答】解:方案一:在公园随机调查100名健身的老年人的健康情况,在公园健身的老年人身体往往都非常好,因此抽样不具有代表性,不能全面反映该小区的老年人健康状况;
方案二:在医院随机调查100名老年人的健康情况,在医院的老年人身体往往都不好,因此抽样不具有代表性,不能全面反映该小区的老年人健康状况;
方案三:在小区内随机调查100名老年人的健康情况,抽样具有代表性,因此能全面反映该小区的老年人健康状况;
故选:C.
【点评】本题考查抽样调查,理解抽样的代表性和普遍性是正确判断的关键.
3.(2024秋 花溪区期末)下列数据中,属于定性数据的是( )
A.小明每周做家务的时间
B.2024年除夕夜春节年欢晚会的收视率
C.某学校老师的平均年龄
D.中学生早餐是否有喝牛奶的习惯
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;应用意识.
【答案】D
【分析】根据定量数据与定性数据的定义解答即可.
【解答】解:A、小明每周做家务的时间是定量数据,不符合题意;
B、2024年除夕夜春节年欢晚会的收视率是定量数据,不符合题意;
C、某学校老师的平均年龄是定量数据,不符合题意;
D、中学生早餐是否有喝牛奶的习惯是定性数据,符合题意;
故选:D.
【点评】本题考查了调查收集数据的过程与方法,熟练掌握统计数据分为定量数据与定性数据以及它们的定义是解题的关键.
4.(2024秋 本溪期末)某校为了了解七年级所有班级学生喜欢阅读的情况,下列做法中比较合理的是( )
A.了解每一名学生喜欢阅读的情况
B.了解每一名女生喜欢阅读的情况
C.了解每一名男生喜欢阅读的情况
D.某一个班当中随机抽取7名男同学和7名女同学,了解他们喜欢阅读的情况
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;数据分析观念.
【答案】D
【分析】根据样本抽样的原则要求,逐项进行判断即可.
【解答】解:A.人数太多不合理,故该选项不符合题意;
B.不能反映全面的情况,不具有代表性,故该选项不符合题意;
C.不能反映全面的情况,不具有代表性,故该选项不符合题意;
D.了解他们喜欢阅读的情况比较合理,故该选项符合题意;
故选:D.
【点评】本题考查样本抽样的原则和要求,掌握样本抽样具有普遍性、代表性和可操作性,是正确判断的前提.
5.(2024秋 新城区校级期末)学校召开运动会,20名学生要统一购买运动鞋,需要的数据是( )
A.每名学生鞋的码数 B.一部分学生鞋的码数
C.每名学生的身高 D.每名学生喜欢的款式
【考点】统计量的选择.
【专题】统计与概率;数据分析观念.
【答案】A
【分析】根据数据的收集方法求解即可.
【解答】解:学校召开运动会,20名学生要统一购买运动鞋,需要的数据是每名学生鞋的码数,
故选:A.
【点评】本题考查了数据的收集与整理.熟练掌握数据的收集方法是解题的关键.
二.填空题(共5小题)
6.(2024秋 茂名期末)下列数据属于定量数据的是 ② (填序号).
①某城市的3月份的空气质量(等级)情况;
②春节档某部电影大年初一当天的票房;
③某市图书馆了解全市中学生最喜欢的图书种类.
【考点】调查收集数据的过程与方法.
【专题】统计与概率;数据分析观念.
【答案】②.
【分析】定量数据是确定数量关系的数据,定性数据是确定事务属性的数据,据此可得答案.
【解答】解:根据定量数据是确定数量关系的数据,定性数据是确定事务属性的数据可知:
①某城市的3月份的空气质量(等级)情况,是定性数据;
②春节档某部电影大年初一当天的票房,是定量数据;
③某市图书馆了解全市中学生最喜欢的图书种类,是定性数据.
故答案为:②.
【点评】本题考查了调查收集数据的过程与方法,根据定性数据的意义做出正确的判断是解题的关键.
7.(2024秋 云岩区期末)小星利用搜索引擎查到电影《志愿军:存亡之战》国庆期间的票房为8.05亿元,这个数据是 定量 数据.(选填“定量”或“定性”)
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;应用意识.
【答案】定量.
【分析】根据定量数据和定性数据的定义进行判断即可.
【解答】解:小星利用搜索引擎查到电影《志愿军:存亡之战》国庆期间的票房为8.05亿元,这个数据是定量数据.
故答案为:定量.
【点评】本题考查调查收集数据的过程与方法,掌握定量数据和定性数据的定义是正确解答的关键.
8.(2024秋 莱西市期末)小芸为了解同学们最感兴趣的在线学习方式,设计了如下的调查问题(选项不完整):
你最感兴趣的一种在线学习方式是( )(单选)
A.B.C.D.其他
她准备从“①在线听课,②在线讨论,③在线学习2~3小时,④用手机在线学习,⑤在线阅读”中选取三个作为该问题的备选答案,合理的选取是 ①②⑤ .(填序号)
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;数据分析观念.
【答案】见试题解答内容
【分析】根据题意可得“①在线听课,②在线讨论,⑤在线阅读”合理.
【解答】解:根据题意可知:
①在线听课,②在线讨论,⑤在线阅读,
作为该问题的备选答案合理,
故答案为:①②⑤.
【点评】本题考查了调查收集数据的过程与方法,解决本题的关键是掌握收集数据的过程与方法.
9.(2024秋 雁塔区校级期末)下面呈现了不同类型的数据,其中是定性数据的是 (2)(4) .
(1)全市所有家庭的户均存款;
(2)某街道各餐馆的卫生情况;
(3)今年全国粮食的总产量;
(4)某单位的所有职位.
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;应用意识.
【答案】(2)(4).
【分析】根据定量数据与定性数据的定义解答即可.
【解答】解:(1)全市所有家庭的户均存款是定量数据;
(2)某街道各餐馆的卫生情况是定性数据;
(3)今年全国粮食的总产量是定量数据;
(4)某单位的所有职位是定性数据.
故答案为:(2)(4).
【点评】本题考查了调查收集数据的过程与方法,熟练掌握统计数据分为定量数据与定性数据以及它们的定义是解题的关键.
10.(2024秋 历下区期中)“科学用眼,保护视力”是青少年珍爱生命的具体表现.某班50名同学的视力检查数据如表所示,其中有两个数据被墨汁遮盖了,以下关于视力的统计量中可以确定的是 ② (填写正确的序号).
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 3 3 6 9 12 10
①平均数
②众数
③方差
【考点】统计量的选择;加权平均数;众数;方差.
【专题】统计的应用;数据分析观念.
【答案】②.
【分析】通过计算视力为4.9、5.0的人数,进行判断,不影响视力出现次数最多的结果,因此不影响众数,同时不影响找第25、26位数据,因此不影响中位数的计算,进而进行选择.
【解答】解:由表格数据可知,成绩为4.9、5.0的人数为50﹣(3+3+6+9+12+10)=7(人),
视力为4.7出现次数最多,因此视力的众数是4.7,
视力从小到大排列后处在第25、26位的两个数都是4.7,因此中位数是4.7,
因此中位数和众数与被遮盖的数据无关,即关于视力的统计量中可以确定的是中位数和众数.
故答案为:②.
【点评】考查中位数、众数、方差、平均数的意义和计算方法,理解各个统计量的实际意义,以及每个统计量所反应数据的特征,是正确判断的前提.
三.解答题(共5小题)
11.(2024秋 郑州期末)为深入学习贯彻2024年全国“两会”精神,培养发展新质生产力所需要的高素质人才,某校组织了以“聚焦两会热点 争做时代青年”为主题的知识竞赛,并随机抽查了八、九年级各10名学生的成绩(单位:分),进行了如下数据的整理与分析.
数据收集:
八年级10名学生的竞赛成绩分别为:85,85,90,75,90,95,80,85,70,95;
九年级10名学生的竞赛成绩分别为:80,95,80,90,85,75,95,80,90,80.
数据整理分析:
平均数 中位数 众数 方差
八年级 85 a 85 60
九年级 85 82.5 b 45
根据以上统计信息,回答下列问题:
(1)表中a= 85 ,b= 80 ;
(2)若该校八年级600名学生均参加了本次知识竞赛,请你估计该校八年级学生本次竞赛成绩在85分及以上的学生人数;
(3)九年级的小芬认为,在此次知识竞赛中,九年级成绩比八年级成绩好,你同意吗?请选择适当的统计量说明理由.
【考点】统计量的选择;用样本估计总体;中位数;众数;方差.
【专题】统计的应用;数据分析观念.
【答案】(1)85,80;(2)420人;(3)同意.
【分析】(1)根据中位数、众数的定义直接求解即可;
(2)用600乘以八年级学生本次竞赛成绩在85分及以上的学生人数所占的比例即可;
(3)根据平均数、中位数、众数以及方差的意义判断即可.
【解答】解:(1)八年级10名学生的竞赛成绩排序:70,75,80,85,85,85,90,90,95,95,
∵中间的数是85,85,
∴中位数a=(85+85)÷2=85,
∵九年级10名学生的竞赛成绩中,80出现次数最多,
∴这组数据的众数是80,即b的值为80,
故答案为:85,80;
(2)600420(人),
答:估计该校八年级学生本次竞赛成绩在85分及以上的学生人数为420人;
(3)同意.
理由:∵两个年级学生竞赛成绩的平均数相同,而九年级学生竞赛成绩的方差小,成绩稳定,
∴九年级成绩比八年级成绩好.
【点评】本题考查了统计表、中位数、众数、平均数和方差,熟练掌握中位数、众数的定义,用将本估计总体等知识是解答此题的关键.
12.(2024秋 和平区期末)为弘扬学科素养,鼓舞和平学子以实际行动诠释和平教育勇攀高峰的信心和勇气,某校八年级共推荐了19位同学参加初赛(校级演讲比赛),初赛成绩排名前10的同学进入决赛.
(1)若初赛结束后,每位同学的分数互不相同.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学成绩的 中位数 ;(填:平均数或众数或中位数)
签号 1 2 3 4 5 6 7 8 9 10
成绩 8.5 9.1 9.2 8.6 9.3 8.8 9.6 8.9 8.7 9.7
签号 11 12 13 14 15 16 17 18 19
成绩 9.8 9.1 8.9 9.3 9.6 8.8 9 8.7 9.3
(2)若初赛结束后,这19位同学的成绩如表:2号选手笑着说:“我的成绩代表着咱们这19位同学的平均水平呀!”14号选手说:“与我同分数的选手最多,我的成绩代表着咱们这19位选手的大众水平嘛!”请问,这19位同学成绩的平均数为 9.1 ,众数为 9.3 ;
(3)已知10号选手与15号选手经常参加此类演讲比赛,她俩想看看近期谁的成绩较好、较稳定,她俩用近三次同时参加演讲比赛的成绩计算得到平均分一样,10号选手的方差为0.5,15号选手的方差为0.38.你认为 15 号选手的成绩比较稳定.
【考点】统计量的选择;算术平均数;中位数;众数;方差.
【专题】统计的应用;数据分析观念;运算能力.
【答案】(1)中位数;
(2)9.1,9.3;
(3)15.
【分析】(1)因为第10名同学的成绩排在中间位置,即是中位数,所以需知道这 19位同学成绩的中位数;
(2)根据平均数公式求解即可;
(3)根据方差的意义分析.
【解答】解:(1)19位同学参加演讲比赛,所得的分数互不相同,取得前10位同学进入决赛,中位数就是第10位,因而要判断自己能否进入决赛,他只需知道这19位同学的中位数就可以;
故答案为:中位数;
(2)19位同学成绩的平均数(8.5+9.1+9.2+8.6+9.3+8.8+9.6+8.9+8.7+9.7+9.8+9.1+8.9+9.3+9.6+8.8+9+8.7+9.3)=9.1,众数为9.3;
故答案为:9.1,9.3;
(3)∵她俩用近三次同时参加演讲比赛的成绩计算得到平均分一样,10号选手的方差为0.5,15号选手的方差为0.38,15号的方差小,
∴15号选手的成绩比较稳定.
故答案为:15.
【点评】本题考查了中位数,平均数,众数,方差,此题不但要求学生会求,而且要求掌握方差、平均数、众数的运用.
13.(2024 当阳市模拟)为培养学生的数学思维,激发学生学习数学的兴趣,我校某班开展了学生数学讲题比赛,分别从男同学和女同学中各选出10位选手参赛,成绩如下:
男同学:85,85,90,75,90,95,80,85,70,95;
女同学:80,95,80,90,85,75,95,80,90,80.
数据整理分析如表:
平均数 中位数 众数 方差
男同学 85 a 85 60
女同学 85 82.5 b 45
根据以上统计信息,回答下列问题:
(1)表中a= 85 ,b= 80 .
(2)女同学小红参加了本次讲题比赛,已知她的成绩在女同学中是中等偏上,则小红的成绩最低可能为 82.5 分.
(3)小红认为在此次讲题比赛中,女同学成绩比男同学成绩好,你同意吗?请选择适当的统计量说明理由.
【考点】统计量的选择;中位数;众数;方差.
【专题】统计的应用;数据分析观念.
【答案】(1)85,80;
(2)82.5;
(3)同意,理由见解析.
【分析】(1)根据中位数、众数的定义直接求解即可;
(2)根据中位数的定义判断即可;
(3)根据方差的意义解答即可.
【解答】解:(1)把男同学的成绩从小到大排列为:70,75,80,85,85,85,90,90,95,95,故中位数为a85,
女同学的成绩中80出现的次数最多,故众数b=80;
故答案为:85,80;
(2)小红参加了本次讲题比赛,已知她的成绩是中等偏上,则小红的成绩最低可能为82.5分;
故答案为:82.5;
(3)同意,理由如下:
因为女同学成绩的方差小于男同学的,成绩波动小,所以女同学的成绩更好.
【点评】本题考查了统计量的选择、中位数、众数、方差等知识,熟练掌握中位数、众数、方差的定义是解答此题的关键.
14.(2024秋 保定期中)嘉琪家的猕猴桃成熟了.嘉琪的爸爸将自家猕猴桃挂在网上销售,原计划是每天卖200kg,但是实际销售受到各方面因素的影响,与原计划有出入.下表是嘉琪记录的某周销售情况(超出计划记为正,不足记为负).
星期 一 二 三 四 五 六 日
与原计划的差值/kg +8 +7 ﹣4 ﹣6 +1 +3 ﹣3
(1)根据表中的数据,这周猕猴桃一共卖了多少kg?
(2)根据表中的数据,这周猕猴桃销售最多的一天比销售最少的一天多销售了多少kg?
(3)若嘉琪家的猕猴桃以5元/kg的价格出售,嘉琪的爸爸通过计算,得出猕猴桃的成本为2元/kg,则这一周嘉琪家卖出的猕猴桃能赚多少元?
【考点】调查收集数据的过程与方法;正数和负数.
【专题】统计与概率;数据分析观念.
【答案】(1)1406kg;
(2)14kg;
(3)4218元.
【分析】(1)用7天的计划销量加上7天的出入量即可;
(2)用表格中最大的数减去最小的数即可;
(3)用销售量乘以每千克的利润即可.
【解答】解:(1)根据表中的数据进行计算如下:
200×7+(8+7﹣4﹣6+1+3﹣3)=1400+6=1406(kg).
答:这周猕猴桃一共卖了1406kg.
(2)8﹣(﹣6)=14(kg).
答:多销售14kg.
(3)1406×(5﹣2)=1406×3=4218(元).
答:这一周嘉琪家卖出的猕猴桃能赚4218元.
【点评】本题考查了有理数混合运算的应用,根据题意列出算式是解答本题的关键.
15.(2024秋 东平县期中)为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如图所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(写出求a的计算过程);
(3)从下表中选择合适的统计量,说明哪个班的成绩更均匀.
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
【考点】统计量的选择;中位数;众数;方差.
【专题】统计的应用;应用意识.
【答案】(1)(2)班学生中测试成绩为(10分)的人数是6人
(2)a=8,b=9,c=8
(3)(1)班成绩更均匀,见解析.
【分析】(1)根据条形统计图求出两班的总人数,结合扇形统计图占比即可得到答案;
(2)根据条形统计图人数找到最中间的项及扇形统计图占比最大的即可得到b,c,利用加权平均数计算公式即可得到a,即可得到答案;
(3)根据方差的意义判断即可得到答案.
【解答】解:(1)由题意知,(1)班和(2)班人数相等,
为:5+10+19+12+4=50(人),
∴(2)班学生中测试成绩为(10分)的人数为:50×(1﹣28%﹣22%﹣24%﹣14%)=6(人),
答:(2)班学生中测试成绩为(10分)的人数是6人;
(2)由题意知,a(6×10+50×28%×9+50×22%×8+50×24%×7+50×14%×6)=8,
由题意可得扇形统计图中(9分)的人数占28%最大,条形统计图中5+10<25<26<5+10+19,
∴b=9;c=8;
答:a,b,c的值分别为8,9,8;
(3)由题意可得,
∵1.16<1.56,
∴(1)班成绩更均匀.
【点评】本题考查直方图与扇形统计图共存求解问题,求平均数,求众数,求中位数及根据方差判断稳定性,解题的关键是看懂两个图及熟练在掌握方差越小,数据分布越均匀.
21世纪教育网(www.21cnjy.com)
