立体图形-- 不规则物体和立体组合图形常考考点 模拟练 2024--2025学年小学数学统小升初会考复习备考
文档属性
| 名称 | 立体图形-- 不规则物体和立体组合图形常考考点 模拟练 2024--2025学年小学数学统小升初会考复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 621.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 16:08:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
立体图形-- 不规则物体和立体组合图形常考考点 模拟练
2024--2025学年小学数学统小升初会考复习备考
一、解答题
1.如图,一个圆柱体零件遭到了粗野的破坏,它被沿着底面直径和高切去了一部分,横截面和底面平行且直径为4厘米,求这个残破图形的体积。(单位:厘米)
2.高铝砖是一种新型材料烧制成的建筑材料,具有耐高温的优点,经常用于高温窑炉内衬和作为装饰材料等。下面是某公司生产的一种高铝砖的样式图。这样一块高铝砖的体积是多少立方厘米?
3.有一个长方体木箱靠墙放置,木箱角上靠墙放有一个小正方体。
(1)求小正方体和长方体露在外面的面积之和。
(2)求小正方体和长方体的体积之和。
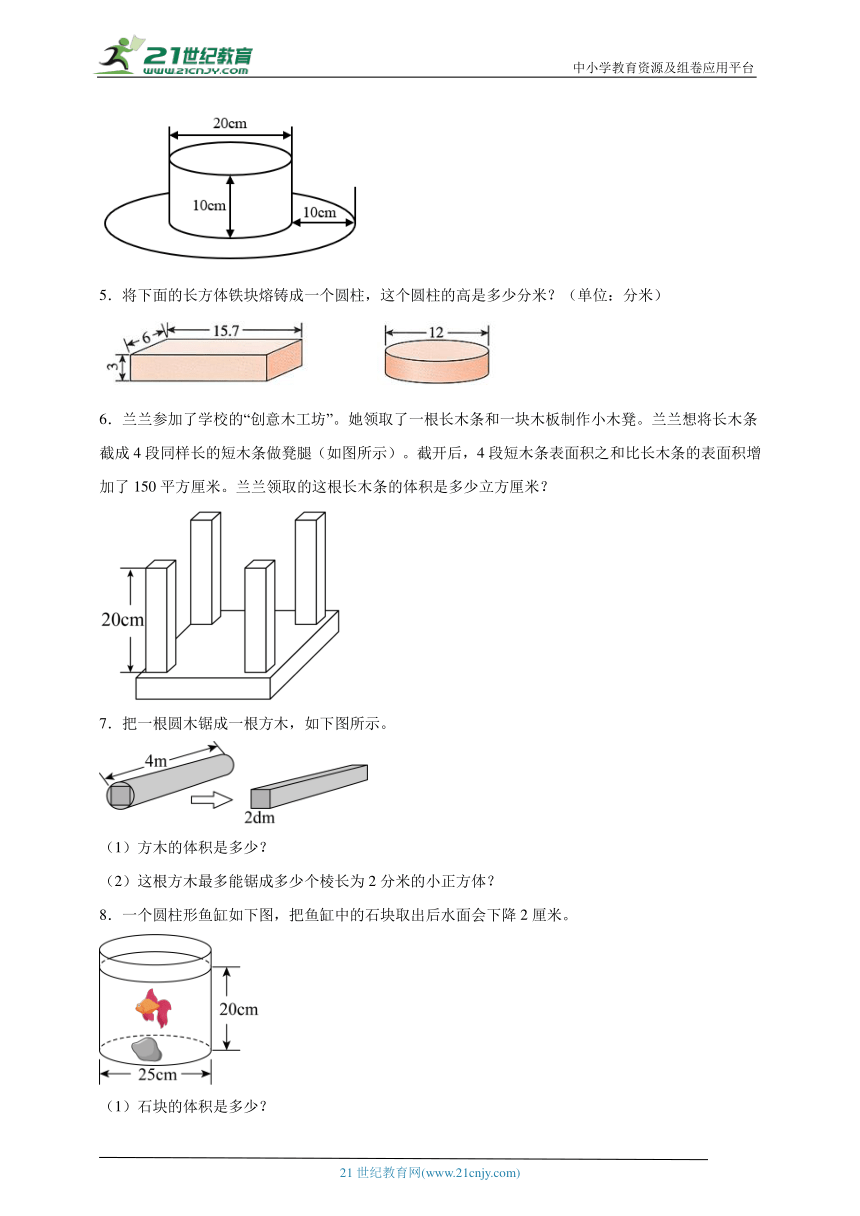
4.学校艺术节时,实验小学的同学们都积极参加了创意制作。芳芳设计了一顶帽子(尺寸如下图),至少需要多少平方厘米的材料?
5.将下面的长方体铁块熔铸成一个圆柱,这个圆柱的高是多少分米?(单位:分米)
6.兰兰参加了学校的“创意木工坊”。她领取了一根长木条和一块木板制作小木凳。兰兰想将长木条截成4段同样长的短木条做凳腿(如图所示)。截开后,4段短木条表面积之和比长木条的表面积增加了150平方厘米。兰兰领取的这根长木条的体积是多少立方厘米?
7.把一根圆木锯成一根方木,如下图所示。
(1)方木的体积是多少?
(2)这根方木最多能锯成多少个棱长为2分米的小正方体?
8.一个圆柱形鱼缸如下图,把鱼缸中的石块取出后水面会下降2厘米。
(1)石块的体积是多少?
(2)取出鱼后,鱼缸里的水又下降2.2厘米,鱼的体积是多少?
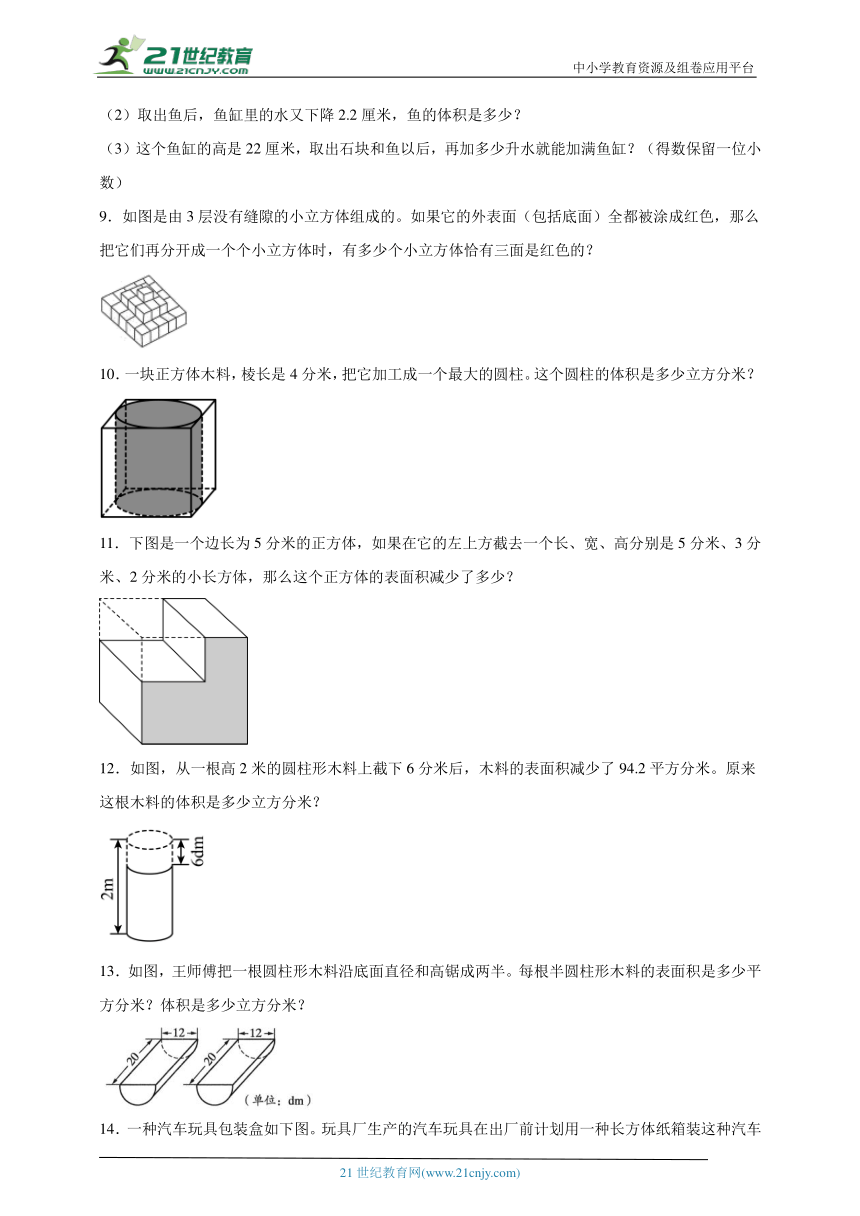
(3)这个鱼缸的高是22厘米,取出石块和鱼以后,再加多少升水就能加满鱼缸?(得数保留一位小数)
9.如图是由3层没有缝隙的小立方体组成的。如果它的外表面(包括底面)全都被涂成红色,那么把它们再分开成一个个小立方体时,有多少个小立方体恰有三面是红色的?
10.一块正方体木料,棱长是4分米,把它加工成一个最大的圆柱。这个圆柱的体积是多少立方分米?
11.下图是一个边长为5分米的正方体,如果在它的左上方截去一个长、宽、高分别是5分米、3分米、2分米的小长方体,那么这个正方体的表面积减少了多少?
12.如图,从一根高2米的圆柱形木料上截下6分米后,木料的表面积减少了94.2平方分米。原来这根木料的体积是多少立方分米?
13.如图,王师傅把一根圆柱形木料沿底面直径和高锯成两半。每根半圆柱形木料的表面积是多少平方分米?体积是多少立方分米?
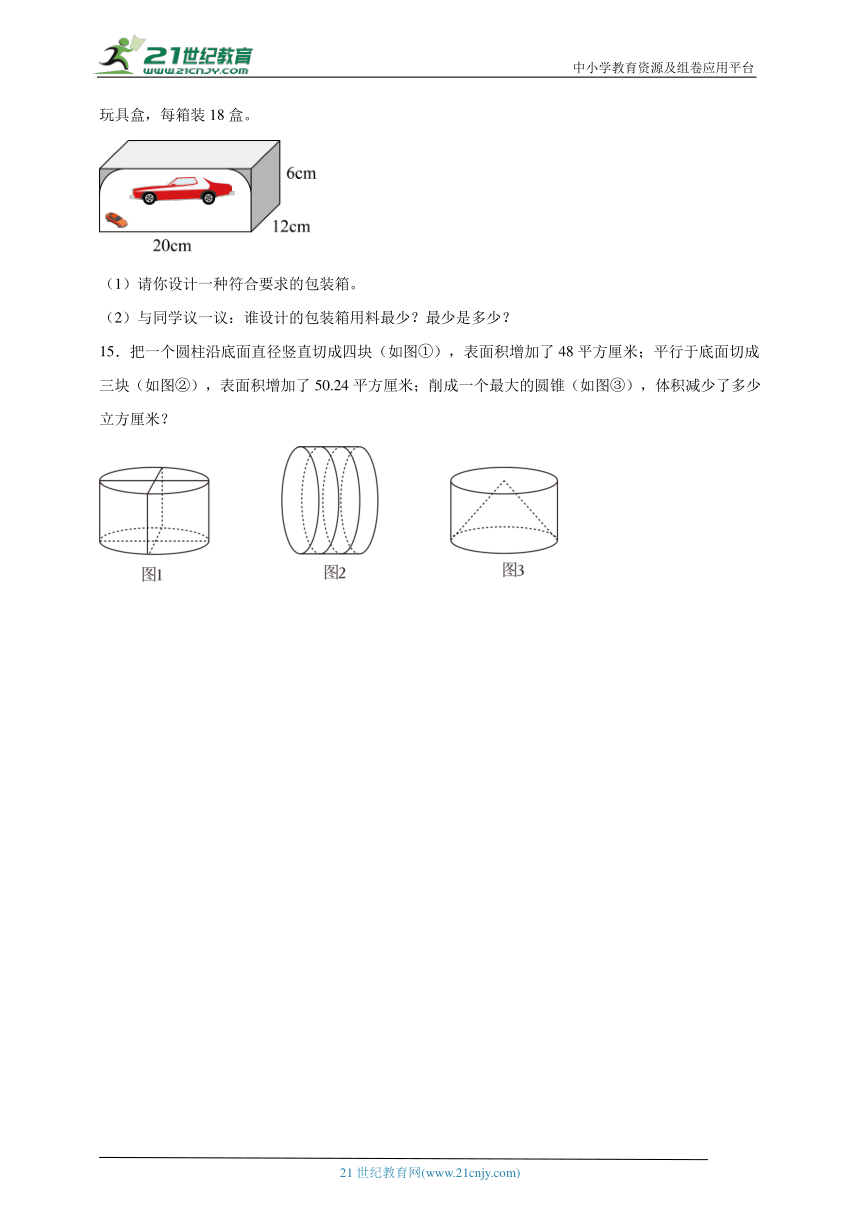
14.一种汽车玩具包装盒如下图。玩具厂生产的汽车玩具在出厂前计划用一种长方体纸箱装这种汽车玩具盒,每箱装18盒。
(1)请你设计一种符合要求的包装箱。
(2)与同学议一议:谁设计的包装箱用料最少?最少是多少?
15.把一个圆柱沿底面直径竖直切成四块(如图①),表面积增加了48平方厘米;平行于底面切成三块(如图②),表面积增加了50.24平方厘米;削成一个最大的圆锥(如图③),体积减少了多少立方厘米?
参考答案
1.106.76立方厘米
【分析】圆柱的体积V=πr2h,可通过添补的方法,用高为11厘米的圆柱体积减去高为5厘米的圆柱体积的一半即可。
【详解】4÷2=2(厘米)
3.14×22×11-3.14×22×5÷2
=12.56×11-12.56×2.5
=138.16-31.4
=106.76(立方厘米)
答:这个残破图形的体积是106.76立方厘米。
【点睛】此题考查圆柱体积的计算,也可用分割法求解。牢记圆柱的体积公式是解题关键。
2.156250立方厘米
【分析】观察图形可知,高铝砖的体积=长为(25+25+25)厘米、宽为50厘米、高50厘米的长方体的体积-长为25厘米、宽为50厘米、高为(50-25)厘米的长方体的体积,根据长方体的体积公式V=abh,代入数据计算求解。
【详解】(25+25+25)×50×50-(50-25)×25×50
=75×50×50-25×25×50
=187500-31250
=156250(立方厘米)
答:这样一块高铝砖的体积是156250立方厘米。
3.(1)98cm2;
(2)152cm3
【分析】(1)长方体露在外面的面是前面、右面和上面,其中上面被小正方体覆盖了一个小正方形的面,所以露在外面的总面积就是长方体的三个面和正方体的2个面;
(2)长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,根据公式计算出长方体和正方体的体积和即可。
【详解】(1)8×3+6×3+8×6+2×2×2
=24+18+48+8
=42+56
=98(cm2)
答:小正方体和长方体露在外面的面积之和是98cm2。
(2)8×6×3+2×2×2
=144+8
=152(cm3)
答:小正方体和长方体的体积之和是152cm3。
【点睛】熟练掌握正方体和长方体的体积计算公式是解题的关键。
4.1884平方厘米
【分析】把圆柱的上底面填补到帽沿的圆环里面,正好组成一个半径为(20÷2+10)厘米的圆,利用圆的面积公式即可求此这部分的面积,再根据圆柱的侧面积公式:S=,代入求出帽子的侧面积,加上前面求出的部分面积,即可求出制作这顶帽子需要材料的面积。
【详解】3.14×20×10+3.14×(20÷2+10)2
=628+3.14×(10+10)2
=628+3.14×202
=628+3.14×400
=628+1256
=1884(平方厘米)
答:至少需要1884平方厘米的材料。
【点睛】此题考查了圆柱表面积的应用,求材料的面积找出帽子的表面积包含哪几部分是解题关键。
5.2.5分米
【分析】根据长方体体积=长×宽×高,求出铁块体积,再根据圆柱的高=体积÷底面积,列式解答即可。
【详解】15.7×6×3÷[3.14×(12÷2)2]
=282.6÷[3.14×62]
=282.6÷[3.14×36]
=282.6÷113.04
=2.5(分米)
答:这个圆柱的高是2.5分米。
【点睛】关键是掌握并灵活运用长方体和圆柱体积公式。
6.2000立方厘米
【分析】一根长木条截成4段同样长的短木条,需要截三次,而表面积增加6个截面的面积,所以每个截面的面积是25平方厘米,由图可知,原长木条的长度是20厘米的4倍,根据V=Sh求出长木条的体积即可。
【详解】150÷[(4-1)×2]×(20×4)
=150÷6×80
=25×80
=2000(立方厘米)
答:兰兰领取的这根长木条的体积是2000立方厘米。
7.(1)160立方分米
(2)20个
【分析】(1)根据长方体体积=底面积×高=横截面×长,求出方木侧面积,再乘方木的长即可,注意统一单位。
(2)方木的侧面是边长2分米的正方形,沿着方木的长每2分米即可锯下1个棱长2分米的小正方体,因此直径用方木的长÷小正方体棱长即可。
【详解】(1)4米=40分米
2×2×40=160(立方分米)
答:方木的体积是160立方分米。
(2)40÷2=20(个)
答:这根方木最多能锯成20个棱长为2分米的小正方体。
8.(1)981.25立方厘米
(2)1079.375立方厘米
(3)3.0升
【分析】(1)根据题意可知,把鱼缸里的石块取出后,水面下降2厘米,水面下降部分的体积,就是石块的体积;根据圆柱的体积公式:体积=底面积×高,代入数据,求出石块的体积;
(2)鱼缸取出鱼后水面又下降2.2厘米,水面下降部分的体积就是鱼的体积,根据圆柱的体积公式,体积=底面积×高,代入数据,求出鱼的体积;
(3)先用20减去取出石块下降的高度,再减去取出鱼水面下降的高度,求出现在水面的高度,再用鱼缸的高度减现在鱼缸里水的高度,求出空白高度,再代入圆柱的体积公式,即可解答。
【详解】(1)3.14×(25÷2)2×2
=3.14×12.52×2
=3.14×156.25×2
=490.625×2
=981.25(立方厘米)
答:石块的体积是981.25立方厘米。
(2)3.14×(25÷2)2×2.2
=3.14×12.52×2.2
=3.14×156.25×2.2
=490.625×2.2
=1079.375(立方厘米)
答:鱼的体积是1079.375立方厘米。
(3)3.14×(25÷2)2×[22-(20-2-2.2)]
=3.14×12.52×[22-(18-2.2)]
=3.14×156.25×[22-15.8]
=490.625×6.2
=3041.875(立方厘米)
3041.875立方厘米=3.041875升
3.041875升≈3.0升
答:再加3.0升水就能加满鱼缸。
9.16个
【分析】观察上图可知,从下往上数,第一层最外围(不含四个角)的小正方体都是三面是红色的,共有3×4=12(个);第二层4个角上的小正方体是三面是红色,共有4个;第三层的小正方体是五面是红色,没有三面是红色的小正方体;所以三面是红色的小正方体共有12+4=16(个),据此即可解答。
【详解】3×4+4
=12+4
=16(个)
答:12个小立方体恰有三面是红色的。
10.50.24立方分米
【分析】根据正方体的特征、圆柱的特征可知,把一块正方体木料削成一个最大的圆柱,也就是削成的圆柱的底面直径和高都等于正方体的棱长,根据圆柱的体积公式:,把数据代入公式解答。
【详解】
(立方分米)
答:这个圆柱的体积是50.24立方分米。
11.12平方分米
【分析】看图可知,表面积减少了4个小长方形,里面又出现了2个小长方形,因此表面积最终减少了2个长是3分米,宽是2分米的小长方形,根据长方形面积=长×宽,求出一个小长方形的面积,再乘2即可。
【详解】3×2×2=12(平方分米)
答:这个正方体的表面积减少了12平方分米。
12.392.5立方分米
【分析】由图可知,截去木料后的表面积比原来圆柱的表面积减少了被截去小圆柱的侧面积,“”则“”把数据代入公式求出圆柱的底面半径,最后利用“”求出原来这根木料的体积,据此解答。
【详解】2米=20分米
94.2÷3.14÷6÷2
=30÷6÷2
=5÷2
=2.5(分米)
3.14×2.52×20
=3.14×6.25×20
=19.625×20
=392.5(立方分米)
答:原来这根木料的体积是392.5立方分米。
13.表面积:729.84平方分米;体积是:1130.4立方分米
【分析】据图可知,半圆柱的表面积等于圆柱侧面积的一半加上圆柱的一个底面积再加上一个长是20分米宽是12分米的长方形的面积,据此结合圆柱的侧面积=πdh,圆柱的底面积=π(d÷2)2,长方形的面积=长×宽列式求出表面积;半圆柱的体积等于圆柱体积的一半,根据圆柱的体积=π(d÷2)2h列式计算即可。
【详解】3.14×12×20÷2+3.14×(12÷2)2+20×12
=37.68×20÷2+3.14×62+240
=753.6÷2+3.14×36+240
=376.8+113.04+240
=729.84(平方分米)
3.14×(12÷2)2×20÷2
=3.14×62×20÷2
=3.14×36×20÷2
=113.04×20÷2
=2260.8÷2
=1130.4(立方分米)
答:每根半圆柱形木料的表面积是729.84平方分米,体积是1130.4立方分米。
14.(1)包装箱的长180厘米;宽12厘米;高12厘米(答案不唯一)
(2)包装箱长20厘米、宽36厘米,高36厘米;最少5472平方厘米
【分析】
(1)如图,可以设计一种能放下2层汽车玩具盒的包装箱,包装箱的长=汽车玩具盒的长×9,包装箱的宽=汽车玩具盒的宽,包装箱的高=汽车玩具盒的高×2,据此分析,答案不唯一。
(2)要想用料最少,尽可能的将玩具盒较大较多的面拼起来,如图、、三种拼法,根据长方体表面积=(长×宽+长×高+宽×高)×2,分别计算出表面积,比较即可。
【详解】(1)20×9=180(厘米)
6×2=12(厘米)
答:可以设计一种长180厘米,宽12厘米,高12厘米的包装箱。
(2)长:20厘米
宽:12×3=36(厘米)
高:6×6=36(厘米)
(20×36+20×36+36×36)×2
=(720+720+1296)×2
=2736×2
=5472(平方厘米)
长:20×2=40(厘米)
宽:12×3=36(厘米)
高:6×3=18(厘米)
(40×36+40×18+36×18)×2
=(1440+720+648)×2
=2808×2
=5616(平方厘米)
长:20×3=60(厘米)
宽:12×3=36(厘米)
高:6×2=12(厘米)
(60×36+60×12+36×12)×2
=(2160+720+432)×2
=3312×2
=6624(平方厘米)
6624>5616>5472
答:当包装箱长20厘米、宽36厘米,高36厘米时用料最少,最少是5472平方厘米。
【点睛】关键是熟悉长方体特征,掌握并灵活运用长方体表面积公式。
15.25.12立方厘米
【分析】根据图②的切分方法可知,增加的表面积是4个圆柱的底面的面积,先用增加的表面积除以4,求出圆柱的底面积,再根据圆的面积公式S=πr2,求出半径的平方即r2的值,进而推导出圆的半径;
根据图①的切分方法可知,增加的表面积是以圆柱的高的长度为长,底面半径的长度为宽的8个长方形的面积,先用增加的表面积除以8,再除以半径,即可求出圆柱的高;
把这个圆柱削成一个最大的圆锥,则圆柱和圆锥等底等高,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,求出圆柱和圆锥的体积,再相减,即是减少的体积。
【详解】底面积:50.24÷4=12.56(平方厘米)
半径的平方:12.56÷3.14=4(平方厘米)
因为4=2×2,所以圆的半径是2厘米;
圆柱的高:48÷8÷2=3(厘米)
减少的体积:
3.14×22×3-×3.14×22×3
=3.14×4×3-×3.14×4×3
=37.68-12.56
=25.12(立方厘米)
答:体积减小了25.12立方厘米。
【点睛】掌握圆柱切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,利用公式求出圆柱的底面半径和高,再根据等底等高的圆柱、圆锥的体积关系求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
立体图形-- 不规则物体和立体组合图形常考考点 模拟练
2024--2025学年小学数学统小升初会考复习备考
一、解答题
1.如图,一个圆柱体零件遭到了粗野的破坏,它被沿着底面直径和高切去了一部分,横截面和底面平行且直径为4厘米,求这个残破图形的体积。(单位:厘米)
2.高铝砖是一种新型材料烧制成的建筑材料,具有耐高温的优点,经常用于高温窑炉内衬和作为装饰材料等。下面是某公司生产的一种高铝砖的样式图。这样一块高铝砖的体积是多少立方厘米?
3.有一个长方体木箱靠墙放置,木箱角上靠墙放有一个小正方体。
(1)求小正方体和长方体露在外面的面积之和。
(2)求小正方体和长方体的体积之和。
4.学校艺术节时,实验小学的同学们都积极参加了创意制作。芳芳设计了一顶帽子(尺寸如下图),至少需要多少平方厘米的材料?
5.将下面的长方体铁块熔铸成一个圆柱,这个圆柱的高是多少分米?(单位:分米)
6.兰兰参加了学校的“创意木工坊”。她领取了一根长木条和一块木板制作小木凳。兰兰想将长木条截成4段同样长的短木条做凳腿(如图所示)。截开后,4段短木条表面积之和比长木条的表面积增加了150平方厘米。兰兰领取的这根长木条的体积是多少立方厘米?
7.把一根圆木锯成一根方木,如下图所示。
(1)方木的体积是多少?
(2)这根方木最多能锯成多少个棱长为2分米的小正方体?
8.一个圆柱形鱼缸如下图,把鱼缸中的石块取出后水面会下降2厘米。
(1)石块的体积是多少?
(2)取出鱼后,鱼缸里的水又下降2.2厘米,鱼的体积是多少?
(3)这个鱼缸的高是22厘米,取出石块和鱼以后,再加多少升水就能加满鱼缸?(得数保留一位小数)
9.如图是由3层没有缝隙的小立方体组成的。如果它的外表面(包括底面)全都被涂成红色,那么把它们再分开成一个个小立方体时,有多少个小立方体恰有三面是红色的?
10.一块正方体木料,棱长是4分米,把它加工成一个最大的圆柱。这个圆柱的体积是多少立方分米?
11.下图是一个边长为5分米的正方体,如果在它的左上方截去一个长、宽、高分别是5分米、3分米、2分米的小长方体,那么这个正方体的表面积减少了多少?
12.如图,从一根高2米的圆柱形木料上截下6分米后,木料的表面积减少了94.2平方分米。原来这根木料的体积是多少立方分米?
13.如图,王师傅把一根圆柱形木料沿底面直径和高锯成两半。每根半圆柱形木料的表面积是多少平方分米?体积是多少立方分米?
14.一种汽车玩具包装盒如下图。玩具厂生产的汽车玩具在出厂前计划用一种长方体纸箱装这种汽车玩具盒,每箱装18盒。
(1)请你设计一种符合要求的包装箱。
(2)与同学议一议:谁设计的包装箱用料最少?最少是多少?
15.把一个圆柱沿底面直径竖直切成四块(如图①),表面积增加了48平方厘米;平行于底面切成三块(如图②),表面积增加了50.24平方厘米;削成一个最大的圆锥(如图③),体积减少了多少立方厘米?
参考答案
1.106.76立方厘米
【分析】圆柱的体积V=πr2h,可通过添补的方法,用高为11厘米的圆柱体积减去高为5厘米的圆柱体积的一半即可。
【详解】4÷2=2(厘米)
3.14×22×11-3.14×22×5÷2
=12.56×11-12.56×2.5
=138.16-31.4
=106.76(立方厘米)
答:这个残破图形的体积是106.76立方厘米。
【点睛】此题考查圆柱体积的计算,也可用分割法求解。牢记圆柱的体积公式是解题关键。
2.156250立方厘米
【分析】观察图形可知,高铝砖的体积=长为(25+25+25)厘米、宽为50厘米、高50厘米的长方体的体积-长为25厘米、宽为50厘米、高为(50-25)厘米的长方体的体积,根据长方体的体积公式V=abh,代入数据计算求解。
【详解】(25+25+25)×50×50-(50-25)×25×50
=75×50×50-25×25×50
=187500-31250
=156250(立方厘米)
答:这样一块高铝砖的体积是156250立方厘米。
3.(1)98cm2;
(2)152cm3
【分析】(1)长方体露在外面的面是前面、右面和上面,其中上面被小正方体覆盖了一个小正方形的面,所以露在外面的总面积就是长方体的三个面和正方体的2个面;
(2)长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,根据公式计算出长方体和正方体的体积和即可。
【详解】(1)8×3+6×3+8×6+2×2×2
=24+18+48+8
=42+56
=98(cm2)
答:小正方体和长方体露在外面的面积之和是98cm2。
(2)8×6×3+2×2×2
=144+8
=152(cm3)
答:小正方体和长方体的体积之和是152cm3。
【点睛】熟练掌握正方体和长方体的体积计算公式是解题的关键。
4.1884平方厘米
【分析】把圆柱的上底面填补到帽沿的圆环里面,正好组成一个半径为(20÷2+10)厘米的圆,利用圆的面积公式即可求此这部分的面积,再根据圆柱的侧面积公式:S=,代入求出帽子的侧面积,加上前面求出的部分面积,即可求出制作这顶帽子需要材料的面积。
【详解】3.14×20×10+3.14×(20÷2+10)2
=628+3.14×(10+10)2
=628+3.14×202
=628+3.14×400
=628+1256
=1884(平方厘米)
答:至少需要1884平方厘米的材料。
【点睛】此题考查了圆柱表面积的应用,求材料的面积找出帽子的表面积包含哪几部分是解题关键。
5.2.5分米
【分析】根据长方体体积=长×宽×高,求出铁块体积,再根据圆柱的高=体积÷底面积,列式解答即可。
【详解】15.7×6×3÷[3.14×(12÷2)2]
=282.6÷[3.14×62]
=282.6÷[3.14×36]
=282.6÷113.04
=2.5(分米)
答:这个圆柱的高是2.5分米。
【点睛】关键是掌握并灵活运用长方体和圆柱体积公式。
6.2000立方厘米
【分析】一根长木条截成4段同样长的短木条,需要截三次,而表面积增加6个截面的面积,所以每个截面的面积是25平方厘米,由图可知,原长木条的长度是20厘米的4倍,根据V=Sh求出长木条的体积即可。
【详解】150÷[(4-1)×2]×(20×4)
=150÷6×80
=25×80
=2000(立方厘米)
答:兰兰领取的这根长木条的体积是2000立方厘米。
7.(1)160立方分米
(2)20个
【分析】(1)根据长方体体积=底面积×高=横截面×长,求出方木侧面积,再乘方木的长即可,注意统一单位。
(2)方木的侧面是边长2分米的正方形,沿着方木的长每2分米即可锯下1个棱长2分米的小正方体,因此直径用方木的长÷小正方体棱长即可。
【详解】(1)4米=40分米
2×2×40=160(立方分米)
答:方木的体积是160立方分米。
(2)40÷2=20(个)
答:这根方木最多能锯成20个棱长为2分米的小正方体。
8.(1)981.25立方厘米
(2)1079.375立方厘米
(3)3.0升
【分析】(1)根据题意可知,把鱼缸里的石块取出后,水面下降2厘米,水面下降部分的体积,就是石块的体积;根据圆柱的体积公式:体积=底面积×高,代入数据,求出石块的体积;
(2)鱼缸取出鱼后水面又下降2.2厘米,水面下降部分的体积就是鱼的体积,根据圆柱的体积公式,体积=底面积×高,代入数据,求出鱼的体积;
(3)先用20减去取出石块下降的高度,再减去取出鱼水面下降的高度,求出现在水面的高度,再用鱼缸的高度减现在鱼缸里水的高度,求出空白高度,再代入圆柱的体积公式,即可解答。
【详解】(1)3.14×(25÷2)2×2
=3.14×12.52×2
=3.14×156.25×2
=490.625×2
=981.25(立方厘米)
答:石块的体积是981.25立方厘米。
(2)3.14×(25÷2)2×2.2
=3.14×12.52×2.2
=3.14×156.25×2.2
=490.625×2.2
=1079.375(立方厘米)
答:鱼的体积是1079.375立方厘米。
(3)3.14×(25÷2)2×[22-(20-2-2.2)]
=3.14×12.52×[22-(18-2.2)]
=3.14×156.25×[22-15.8]
=490.625×6.2
=3041.875(立方厘米)
3041.875立方厘米=3.041875升
3.041875升≈3.0升
答:再加3.0升水就能加满鱼缸。
9.16个
【分析】观察上图可知,从下往上数,第一层最外围(不含四个角)的小正方体都是三面是红色的,共有3×4=12(个);第二层4个角上的小正方体是三面是红色,共有4个;第三层的小正方体是五面是红色,没有三面是红色的小正方体;所以三面是红色的小正方体共有12+4=16(个),据此即可解答。
【详解】3×4+4
=12+4
=16(个)
答:12个小立方体恰有三面是红色的。
10.50.24立方分米
【分析】根据正方体的特征、圆柱的特征可知,把一块正方体木料削成一个最大的圆柱,也就是削成的圆柱的底面直径和高都等于正方体的棱长,根据圆柱的体积公式:,把数据代入公式解答。
【详解】
(立方分米)
答:这个圆柱的体积是50.24立方分米。
11.12平方分米
【分析】看图可知,表面积减少了4个小长方形,里面又出现了2个小长方形,因此表面积最终减少了2个长是3分米,宽是2分米的小长方形,根据长方形面积=长×宽,求出一个小长方形的面积,再乘2即可。
【详解】3×2×2=12(平方分米)
答:这个正方体的表面积减少了12平方分米。
12.392.5立方分米
【分析】由图可知,截去木料后的表面积比原来圆柱的表面积减少了被截去小圆柱的侧面积,“”则“”把数据代入公式求出圆柱的底面半径,最后利用“”求出原来这根木料的体积,据此解答。
【详解】2米=20分米
94.2÷3.14÷6÷2
=30÷6÷2
=5÷2
=2.5(分米)
3.14×2.52×20
=3.14×6.25×20
=19.625×20
=392.5(立方分米)
答:原来这根木料的体积是392.5立方分米。
13.表面积:729.84平方分米;体积是:1130.4立方分米
【分析】据图可知,半圆柱的表面积等于圆柱侧面积的一半加上圆柱的一个底面积再加上一个长是20分米宽是12分米的长方形的面积,据此结合圆柱的侧面积=πdh,圆柱的底面积=π(d÷2)2,长方形的面积=长×宽列式求出表面积;半圆柱的体积等于圆柱体积的一半,根据圆柱的体积=π(d÷2)2h列式计算即可。
【详解】3.14×12×20÷2+3.14×(12÷2)2+20×12
=37.68×20÷2+3.14×62+240
=753.6÷2+3.14×36+240
=376.8+113.04+240
=729.84(平方分米)
3.14×(12÷2)2×20÷2
=3.14×62×20÷2
=3.14×36×20÷2
=113.04×20÷2
=2260.8÷2
=1130.4(立方分米)
答:每根半圆柱形木料的表面积是729.84平方分米,体积是1130.4立方分米。
14.(1)包装箱的长180厘米;宽12厘米;高12厘米(答案不唯一)
(2)包装箱长20厘米、宽36厘米,高36厘米;最少5472平方厘米
【分析】
(1)如图,可以设计一种能放下2层汽车玩具盒的包装箱,包装箱的长=汽车玩具盒的长×9,包装箱的宽=汽车玩具盒的宽,包装箱的高=汽车玩具盒的高×2,据此分析,答案不唯一。
(2)要想用料最少,尽可能的将玩具盒较大较多的面拼起来,如图、、三种拼法,根据长方体表面积=(长×宽+长×高+宽×高)×2,分别计算出表面积,比较即可。
【详解】(1)20×9=180(厘米)
6×2=12(厘米)
答:可以设计一种长180厘米,宽12厘米,高12厘米的包装箱。
(2)长:20厘米
宽:12×3=36(厘米)
高:6×6=36(厘米)
(20×36+20×36+36×36)×2
=(720+720+1296)×2
=2736×2
=5472(平方厘米)
长:20×2=40(厘米)
宽:12×3=36(厘米)
高:6×3=18(厘米)
(40×36+40×18+36×18)×2
=(1440+720+648)×2
=2808×2
=5616(平方厘米)
长:20×3=60(厘米)
宽:12×3=36(厘米)
高:6×2=12(厘米)
(60×36+60×12+36×12)×2
=(2160+720+432)×2
=3312×2
=6624(平方厘米)
6624>5616>5472
答:当包装箱长20厘米、宽36厘米,高36厘米时用料最少,最少是5472平方厘米。
【点睛】关键是熟悉长方体特征,掌握并灵活运用长方体表面积公式。
15.25.12立方厘米
【分析】根据图②的切分方法可知,增加的表面积是4个圆柱的底面的面积,先用增加的表面积除以4,求出圆柱的底面积,再根据圆的面积公式S=πr2,求出半径的平方即r2的值,进而推导出圆的半径;
根据图①的切分方法可知,增加的表面积是以圆柱的高的长度为长,底面半径的长度为宽的8个长方形的面积,先用增加的表面积除以8,再除以半径,即可求出圆柱的高;
把这个圆柱削成一个最大的圆锥,则圆柱和圆锥等底等高,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,求出圆柱和圆锥的体积,再相减,即是减少的体积。
【详解】底面积:50.24÷4=12.56(平方厘米)
半径的平方:12.56÷3.14=4(平方厘米)
因为4=2×2,所以圆的半径是2厘米;
圆柱的高:48÷8÷2=3(厘米)
减少的体积:
3.14×22×3-×3.14×22×3
=3.14×4×3-×3.14×4×3
=37.68-12.56
=25.12(立方厘米)
答:体积减小了25.12立方厘米。
【点睛】掌握圆柱切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,利用公式求出圆柱的底面半径和高,再根据等底等高的圆柱、圆锥的体积关系求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
