立体图形的认识--长方体和正方体常考考点 模拟练 2024--2025学年小学数学统小升初会考复习备考
文档属性
| 名称 | 立体图形的认识--长方体和正方体常考考点 模拟练 2024--2025学年小学数学统小升初会考复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 421.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 16:08:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
立体图形的认识--长方体和正方体常考考点 模拟练
2024--2025学年小学数学统小升初会考复习备考
一、选择题
1.一种长方体饼干盒,长、宽、高的(如图),买3盒这样的饼干包装成一件礼品,用最节约纸的方式包装,需要包装纸( )。(接口处不计)
A. B. C. D.
2.下面各物体中,不能用“底面积×高”求它体积的物体是( )。
A. B. C. D.
3.如图,封闭玻璃容器里装有液体(单位:cm),竖放时液体刚好成正方体的形状,横放时液体高( )。
A.1.6 B.2 C.6 D.6.4
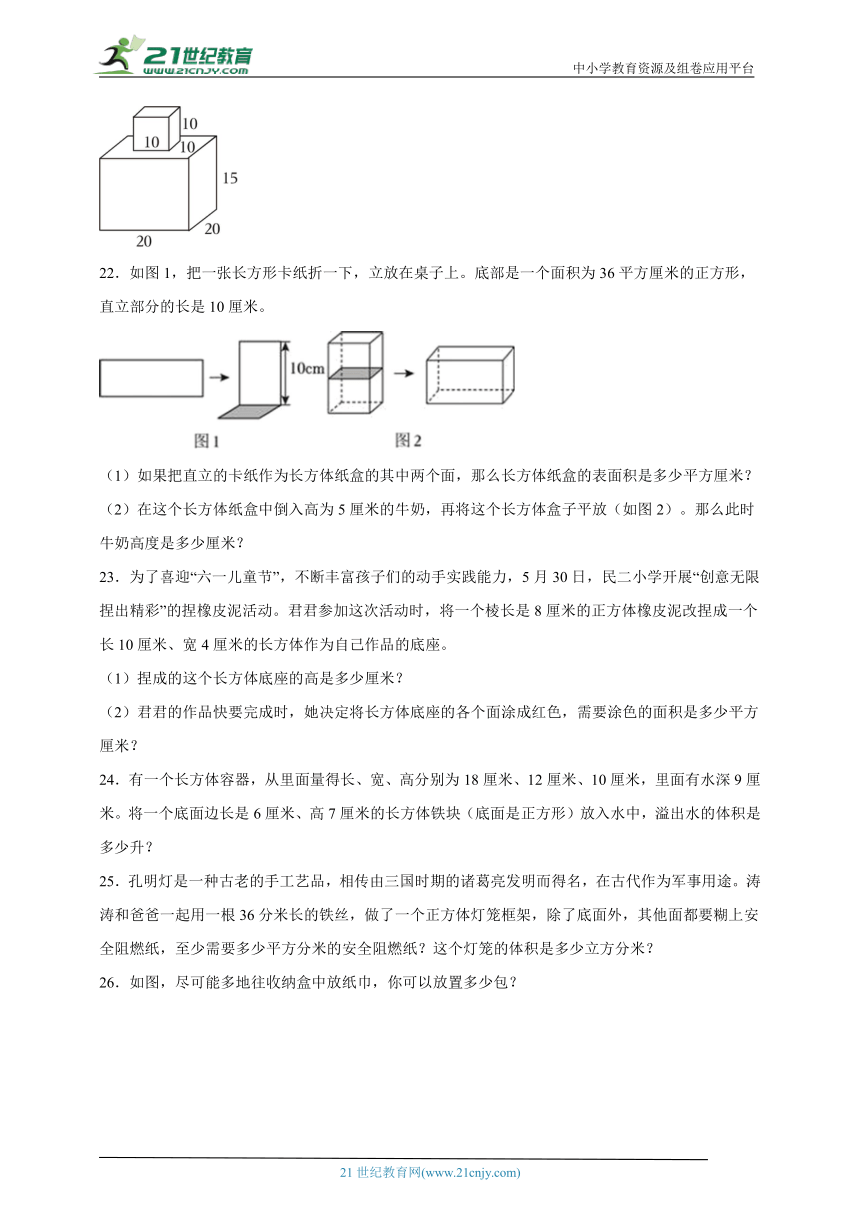
4.一只蚂蚁,沿一个长宽高分别为10cm、8cm、5cm的长方体木块的棱爬行。如果8个顶点都要经过,那么这只蚂蚁最短的爬行路程是( )cm。
A.92 B.56 C.49 D.46
5.一个正方体相对的面分别是1点和2点、3点和4点、5点和6点。游戏规则:在方格棋盘上沿棱按照箭头方向翻动正方体,每次不能后退。开始时正方体如左图那样摆放,最后翻动到如右图所示的位置,此时正方体朝上的点数是( )。
A.6 B.5 C.3 D.4
6.魔方又叫鲁比克方块,是一款风靡全球的机械益智玩具。辰辰是魔方爱好者,他有一款三阶魔方,即3×3×3。可是,他在一次玩耍中不小心掉了一个小正方体,请问魔方的表面积会( )。
A.变大 B.变小 C.不变 D.答案不唯一
7.把两个棱长为的正方体拼成一个长方体后,表面积减少了( )。
A.6 B.9 C.12 D.18
8.一个长方体容器从里面量,它的长是8分米,宽是5分米,高是6分米,如果高减少2分米,那么该容器少装水( )升。
A.240 B.96 C.80 D.60
9.冬冬在一个长方体盒子中装了一些棱长为1分米的正方体(如图),这个盒子的容积是( )。
A.11立方分米 B.19立方分米 C.30立方分米 D.无法确定
10.一个长方体的长,宽,高分别是a厘米,b厘米,h厘米,如果高增加2厘米,则其体积增加( )立方厘米。
A.abh B.2ab C.2ah D.ab(h+2)
11.在一个透明的长方体盒子内放置棱长为1cm的小正方体(如图)。这个长方体盒子的表面积是( )cm2。
A.66 B.60 C.33 D.30
12.五年级的同学们准备去郊外春游,老师要求每位同学都要带足够的水。小明的妈妈给他准备了一瓶2升的矿泉水,为了携带方便小明需要把水分装到小瓶中,如果每个小瓶装550毫升,那么他至少需要( )个这样的小瓶。
A.2 B.3 C.4 D.5
二、填空题
13.丽丽要把下面长方体展开图折成长方体。
(1)如果A面在底面,那么( )面在上面。
(2)用胶带沿棱将所有接缝处进行粘合,她至少需要用( )厘米的胶带。(提示:可以先画一画需要粘合的边再填空。)
14.一个正方体的棱长总和是4.8m,它的表面积是( )m2,体积是( )dm3。
15.把棱长为1dm的正方体木块,切成棱长为1cm的小正方体,可以切成( )块。
16.一个长方体木块的长是15cm,宽是10cm,高是8cm。从这个木块的一头切下一个最大的正方体后,剩下部分的表面积是( )cm2,体积是( )cm3。
17.一个正方体,如果高减少3cm,就变成了一个长方体。这时表面积比原来减少60cm2。原来正方体的体积是( )cm3。
18.如图,正方体的棱长是4cm,从它的一个顶点处挖去一个棱长是2cm的小正方体,所剩下的物体的表面积是( )cm2。
19.在一个底面积为34平方分米,高7分米的长方体容器中,倒入4分米深的水。现将一个铁块完全浸没在水中,水面上升2分米。这个铁块的体积是( )立方分米。
三、解答题
20.一个长方体无盖玻璃缸(如下图),长7分米,宽6分米,高4分米,水深2.8分米。
(1)做这个玻璃缸需要多少平方分米玻璃?(不考虑玻璃厚度)
(2)如果把下图左边这块棱长为4分米的正方体铁块竖直放入缸里,缸里的水会溢出多少升?
21.一个容器由一个内空棱长10厘米的正方体和一个内空长20厘米,宽20厘米,高15厘米的长方体组合形成(如图)。正放时(长方体在下面)水深10厘米,倒放时(正方体在下面,放平)水最深处多少厘米?
22.如图1,把一张长方形卡纸折一下,立放在桌子上。底部是一个面积为36平方厘米的正方形,直立部分的长是10厘米。
(1)如果把直立的卡纸作为长方体纸盒的其中两个面,那么长方体纸盒的表面积是多少平方厘米?
(2)在这个长方体纸盒中倒入高为5厘米的牛奶,再将这个长方体盒子平放(如图2)。那么此时牛奶高度是多少厘米?
23.为了喜迎“六一儿童节”,不断丰富孩子们的动手实践能力,5月30日,民二小学开展“创意无限捏出精彩”的捏橡皮泥活动。君君参加这次活动时,将一个棱长是8厘米的正方体橡皮泥改捏成一个长10厘米、宽4厘米的长方体作为自己作品的底座。
(1)捏成的这个长方体底座的高是多少厘米?
(2)君君的作品快要完成时,她决定将长方体底座的各个面涂成红色,需要涂色的面积是多少平方厘米?
24.有一个长方体容器,从里面量得长、宽、高分别为18厘米、12厘米、10厘米,里面有水深9厘米。将一个底面边长是6厘米、高7厘米的长方体铁块(底面是正方形)放入水中,溢出水的体积是多少升?
25.孔明灯是一种古老的手工艺品,相传由三国时期的诸葛亮发明而得名,在古代作为军事用途。涛涛和爸爸一起用一根36分米长的铁丝,做了一个正方体灯笼框架,除了底面外,其他面都要糊上安全阻燃纸,至少需要多少平方分米的安全阻燃纸?这个灯笼的体积是多少立方分米?
26.如图,尽可能多地往收纳盒中放纸巾,你可以放置多少包?
结合生活实际想一想,我( )(填“同意”或“不同意")小凯的想法。如果同意,请你写出理由;如果不同意,尽可能多地往乙收纳盒中放纸巾,你可以放置多少包?写出你的思考过程,可以写一写,画一画。
27.如图,在一个棱长为5分米的正方体上面的正中间向下挖一个棱长为2分米的正方体小洞,接着在小洞的底面正中间再向下挖一个棱长为1分米的正方体小洞。求挖洞后的几何体的表面积是多少平方分米?
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D A D D C C B
题号 11 12
答案 A C
1.B
【分析】根据长方体表面积的意义可知,把3盒这样的饼干包装成一件礼品,要使需要的包装纸最少,也就是把饼干盒的最大面重合摞起来,拼成一个长3cm,宽2cm,高cm的长方体,根据长方体的表面积公式:,把数据代入公式解答。
【详解】(cm)
(cm2)
需要包装纸42cm2。
故答案为:B
2.C
【分析】根据圆柱、长方体、正方体的体积公式:V=Sh,圆锥的体积公式:V=Sh,据此解答即可。
【详解】
A.是正方体,能用“底面积×高”求体积;
B.可以看作一个长方体减去半个圆柱体的组合图形,能用“底面积×高”求体积;
C.不能用“底面积×高”求体积;
D.由一个长方体和一个正方体组成,能用“底面积×高”求体积。
故答案为:C
3.D
【分析】根据正方体体积=棱长×棱长×棱长,求出液体体积,再根据长方体的高=体积÷底面积,求出横放时液体高即可。
【详解】8×8×8÷(10×8)
=512÷80
=6.4(cm)
故答案为:D
【点睛】关键是掌握并灵活运用长方体和正方体体积公式。
4.D
【分析】长方体有12条棱,8个顶点。一只蚂蚁沿长方体木块的棱爬行,8个顶点都要经过,要想爬行路程最短,就不要爬重复的路线,尽量爬较短的棱。沿着长方体的一个面的棱爬行,只要爬3条棱就可经过4个顶点,这3条棱最短是5+5+8=18cm,这个面即左(或右)面。因此这一只蚂蚁可以沿长方体木块右面的一个顶点开始爬3条棱即18cm,再经过一条长(10cm)爬到左面,再爬3条棱即18cm,就是最短路程。
【详解】根据分析作最短的爬行路线图如下:
5×4+8×2+10
=20+16+10
=46(cm)
那么这只蚂蚁最短的爬行路程是46cm。
故答案为:D
5.A
【分析】根据箭头从左图的位置翻动到右图的位置,先向上翻动1次,再向右翻动2次:向上翻动1次,5点朝上,向右翻动第1次后,2点朝上,再向右翻动1次,6点朝上。所以此时正方体朝上的点数是6。
【详解】由分析可知:
开始时正方体如左图那样摆放,最后翻动到如右图所示的位置,此时正方体朝上的点数是6。
故答案为:A
6.D
【分析】掉了一个小正方体后,由于掉的小正方体原来的位置不同,魔方的表面积会有不同的变化,需要分类讨论。讨论时,先分析增加的部分,再分析减少的部分,最后对比出魔方的表面积是增还是减。
【详解】①掉的小正方体是魔方的8个顶点中的一处,会减少三个小正方形的面积,同时会增加三个小正方形的面积,那么魔方的表面积不变;
②掉的小正方体是魔方每条棱上非顶点位置的一处,会减少2个小正方形的面积,但同时会增加4个小正方形的面积,那么魔方的表面积变大;
③掉的小正方体在魔方每个面的中心位置,会减少1个小正方形的面积,但同时会增加5个小正方形的面积,那么魔方的表面积变大。
综上可知,魔方的表面积可能变大也可能不变,那么答案不唯一。
故答案为:D
7.D
【分析】由题意可知,表面积减少的是正方体的两个面,根据,代入数据求出正方形的面积再乘2即可得解。
【详解】
(cm2)
把两个棱长为的正方体拼成一个长方体后,表面积减少了18。
故答案为:D
8.C
【分析】根据长方体的体积(容积)=长×宽×高,代入数据计算,求出高减少的2分米的空间的大小即可,最后根据1立方分米=1升,将结果换算成升即可。
【详解】8×5×2=80(立方分米)
80立方分米=80升
该容器少装水80升。
故答案为:C
9.C
【分析】根据图可知,长方体盒子的长等于1×5=5分米,宽等于1×3=3分米,高等于1×2=2分米;根据长方体容积公式:体积=长×宽×高,代入数据,即可解答。
【详解】盒子长:1×5=5(分米)
盒子宽:1×3=3(分米)
盒子高:1×2=2(分米)
盒子容积:
5×3×2
=15×2
=30(立方分米)
冬冬在一个长方体盒子中装了一些棱长为1分米的正方体,这个盒子的容积是30立方分米。
故答案为:C
10.B
【分析】如果高增加2厘米,则其增加的体积等于长a厘米、宽b厘米、高2厘米的长方体的体积,根据长方体的体积=长×宽×高,代入数据计算即可解答。
【详解】a×b×2=2ab(立方厘米)
所以一个长方体的长,宽,高分别是a厘米,b厘米,h厘米,如果高增加2厘米,则其体积增加2ab立方厘米。
故答案为:B
11.A
【分析】根据图可知,这个长方体盒子的长等于4个小正方体的棱长和,宽等于3个小正方体的棱长和,高等于3个小正方体的棱长和,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】长:1×4=4(cm),宽:1×3=3(cm);高:1×3=3(cm)。
表面积:
(4×3+4×3+3×3)×2
=(12+12+9)×2
=(24+9)×2
=33×2
=66(cm2)
在一个透明的长方体盒子内放置棱长为1cm的小正方体(如图)。这个长方体盒子的表面积是66cm2。
故答案为:A
12.C
【分析】先将2升换算成2000毫升,再算2000毫升里有多少个550毫升,就需要多少个这样的瓶,所以用2000÷550=3(个)……350(毫升),要全部装完,不管余下多少,也要一个瓶装,因此至少需要3+1=4(个)瓶。据此解答。
【详解】2升=2000毫升
2000÷550=3(个)……350(毫升)
3+1=4(个)
那么他至少需要4个这样的小瓶。
故答案为:C
13.(1)E
(2)66
【分析】(1)根据长方体的特征,相对的面完全相同,据此解答即可;
(2)由题意可知,需要胶带的长度就是长方体所有接缝处的棱长总和。根据题干展开图可得,接缝处的棱长共有4条高、2条长和1条宽,据此进行计算即可。
【详解】(1)如果A面在底面,那么E面在上面。
(2)7×4+14×2+10
=28+28+10
=66(厘米)
则她至少需要用66厘米的胶带。
14. 0.96 64
【分析】正方体的棱长总和除以12求出它的棱长,再根据正方体的表面积=棱长×棱长×6,求出它的表面积,根据正方体的体积=棱长×棱长×棱长,求出它的体积。注意最后要换算单位,高级单位转化为低级单位乘两个单位之间的进率,1m3=1000dm3。
【详解】4.8÷12=0.4(m)
0.4×0.4×6=0.96(m2)
0.4×0.4×0.4=0.064(m3)
0.064m3=64dm3
则它的表面积是0.96m2,体积是64dm3。
15.1000
【分析】根据1dm=10cm,再根据正方体的体积公式:棱长×棱长×棱长,把数代入分别求出正方体木块和小正方体木块的体积,之后用正方体木块的体积除以小正方体木块的体积即可求出可以切成多少块。
【详解】1dm=10cm
10×10×10÷(1×1×1)
=1000÷1
=1000(块)
可以切成1000块。
16. 572 688
【分析】分析题目,从这个长方体木头上切下一个最大的正方体,则正方体的棱长就等于长方体最短的一条棱,即正方体的棱长是8cm,剩下部分的表面积等于原来长方体的表面积减去棱长是8cm的正方体的2个面的面积,剩下部分的体积等于原来长方体的体积减去切下的正方体的体积,据此根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的表面积=棱长×棱长×6,长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长代入数据列式计算即可。
【详解】(15×10+15×8+10×8)×2-8×8×2
=(150+120+80)×2-64×2
=350×2-128
=700-128
=572(cm2)
15×10×8-8×8×8
=150×8-64×8
=1200-512
=688(cm3)
一个长方体木块的长是15cm,宽是10cm,高是8cm。从这个木块的一头切下一个最大的正方体后,剩下部分的表面积是572cm2,体积是688cm3。
17.125
【分析】分析题目,如果正方体的高减少3cm,则表面积就减少了4个相同的长方形的面,这个长方形的长是正方体的棱长、宽是3cm,据此先用60除以4求出一个面的面积,再除以3即可求出正方体的棱长,最后根据正方体的体积=棱长×棱长×棱长,代入数据计算即可。
【详解】60÷4=15(cm2)
15÷3=5(cm)
5×5×5
=25×5
=125(cm3)
因此,这个正方体的体积是125cm3。
18.96
【分析】分析题目,剩下物体的表面积等于棱长是4cm的正方体的表面积,据此结合正方体的表面积=棱长×棱长×6列式计算即可。
【详解】4×4×6
=16×6
=96(cm2)
正方体的棱长是4cm,从它的一个顶点处挖去一个棱长是2cm的小正方体,所剩下的物体的表面积是96cm2。
19.68
【分析】根据题意可知,物体的体积等于上升部分水的体积,上升部分水的体积等于容器的底面积乘上升部分水的高度,已知长方体容器底面积是34平方分米,上升了2分米,代入数据解答即可求出铁块的体积。
【详解】34×2=68(立方分米)
这个铁块的体积是68立方分米。
20.(1)146平方分米;(2)13.6升
【分析】(1)无盖的长方体表面积只有5个面的面积,也就是无盖长方体的表面积=长×宽+长×高×2+宽×高×2,代入数据即可求出做这个玻璃缸需要多少平方分米玻璃;
(2)根据题意可知,正方体的体积+水的体积=长方体无盖玻璃缸的容积+溢出水的体积,根据正方体的体积=棱长×棱长×棱长以及长方体的体积(容积)=长×宽×高,分别求出对应的体积,进而求出溢出水的体积,再把单位换算成升。
【详解】(1)7×6+7×4×2+6×4×2
=42+56+48
=146(平方分米)
答:做这个玻璃缸需要146平方分米玻璃。
(2)4×4×4=64(立方分米)
7×6×2.8=117.6(立方分米)
7×6×4=168(立方分米)
64+117.6-168=13.6(立方分米)
13.6立方分米=13.6升
答:缸里的水会溢出13.6升。
21.17.5厘米
【分析】根据长方体的体积公式:V=长×宽×高计算出水的容积,根据倒置后水的容积不变计算水深即可。先判断出水的容积大于正方体的体积,则水深超过正方体的棱长,在长方体还有一部分水深。用水的容积减去正方体的体积,求出在长方体里面的水的容积,再除以长方体的底面积,即可求出此时长方体中的水深。用正方体的棱长加上此时长方体中的水深,求出水的总深度。
【详解】20×20×10
=400×10
=4000(立方厘米)
10×10×10
=100×10
=1000(立方厘米)
4000-1000=3000(立方厘米)
3000÷(20×20)
=3000÷400
=7.5(厘米)
10+7.5=17.5(厘米)
答:倒放时(正方体在下面,放平)水最深处17.5厘米。
22.(1)312平方厘米
(2)3厘米
【分析】(1)根据长方体的特征可知,长方体有两个面是正方形,那么其他四个侧面是完全相同的长方形。已知这个长方体的底面是面积为36平方厘米的正方形,根据正方形的面积=边长×边长,可知正方形的边长是6厘米,即长方体的长、宽都是6厘米;那么4个侧面都是“10×6”的长方形,根据长方形的面积=长×宽,求出侧面积,再加上2个正方形的面积,即是这个长方体纸盒的表面积。
(2)在这个长方体纸盒中倒入高为5厘米的牛奶,根据长方体的体积=底面积×高,求出牛奶的体积;再将这个长方体盒子平放,即长方体的底面变成“10×6”的长方形,根据长方体的高=体积÷底面积,即可求出此时牛奶的高度。
【详解】(1)因为36=6×6,所以正方形的边长是6厘米。
36×2+10×6×4
=72+240
=312(平方厘米)
答:长方体纸盒的表面积是312平方厘米。
(2)36×5=180(立方厘米)
180÷(10×6)
=180÷60
=3(厘米)
答:此时牛奶高度是3厘米。
23.(1)12.8厘米
(2)438.4平方厘米
【分析】(1)根据体积的意义可知,把正方体橡皮泥捏成长方体后体积不变,正方体的体积公式:正方体的体积=棱长×棱长×棱长,根据长方体的体积=长×宽 ×高可知长方体的高=体积÷(长×宽),据此代入数据计算即可;
(2)根据长方体的表面积公式:长方体的表面积=(长×宽+长×高+宽×高)×2,把数据代入公式解答即可。
【详解】(1)8×8×8÷(10×4)
=64×8÷40
=512÷40
=12.8(厘米)
答:捏成的这个长方体底座的高是12.8厘米。
(2)(10×4+10×12.8+4×12.8)×2
=(40+128+51.2)×2
=219.2×2
=438.4(平方厘米)
答:需要涂色的面积是438.4平方厘米。
24.0.036升
【分析】长方体的体积(容积)=长×宽×高,溢出水的体积=容器中水的体积+长方体铁块的体积-长方体容器的容积,最后根据“1升=1000立方厘米”把单位转化为“升”,据此解答。
【详解】18×12×9+6×6×7-18×12×10
=216×9+36×7-216×10
=1944+252-2160
=2196-2160
=36(立方厘米)
36立方厘米=0.036升
答:溢出水的体积是0.036升。
25.45平方分米;27立方分米
【分析】由正方体的棱长和=棱长×12可推导出,棱长=正方体的棱长和÷12,据此先用铁丝长度除以12求出正方体灯笼的棱长;正方体灯笼5个面要糊上安全阻燃纸,再用棱长×棱长×5即可求出安全阻燃纸的面积;最后根据正方体的体积=棱长×棱长×棱长,求出这个灯笼的体积。
【详解】(分米)
(平方分米)
(立方分米)
答:至少需要45平方分米的安全阻燃纸。这个灯笼的体积是27立方分米。
26.不同意;7包
【分析】联系生活实际可知,纸巾的形状是固定的有可能收纳盒的容积够,但是纸巾装不下,所以不能直接用收纳盒的容积除以每包纸巾的体积,应该计算收纳盒内部的长对应能放几包,内部的宽对应能放几包,最多能放几层,据此解答即可。
【详解】我不同意小凯的想法。
15÷5=3(包)
17-7=10(厘米)
10÷5=2(包)
15÷7=2(包)……1(厘米)
因为3<4,所以只能放一层纸巾,共可以放置的数量为:
2×2+3
=4+3
=7(包)
如下图所示:
答:最多可以放置7包。
27.170平方分米
【分析】分析题目,通过平移可知:这个图形的表面积就等于棱长是5分米的正方体的表面积加棱长是1分米的正方体的前后左右4个面加棱长是2分米的正方体的前后左右4个面,据此结合正方体的表面积=棱长×棱长×6列式计算即可。
【详解】5×5×6+1×1×4+2×2×4
=25×6+1×4+4×4
=150+4+16
=170(平方分米)
答:挖洞后的几何体的表面积是170平方分米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
立体图形的认识--长方体和正方体常考考点 模拟练
2024--2025学年小学数学统小升初会考复习备考
一、选择题
1.一种长方体饼干盒,长、宽、高的(如图),买3盒这样的饼干包装成一件礼品,用最节约纸的方式包装,需要包装纸( )。(接口处不计)
A. B. C. D.
2.下面各物体中,不能用“底面积×高”求它体积的物体是( )。
A. B. C. D.
3.如图,封闭玻璃容器里装有液体(单位:cm),竖放时液体刚好成正方体的形状,横放时液体高( )。
A.1.6 B.2 C.6 D.6.4
4.一只蚂蚁,沿一个长宽高分别为10cm、8cm、5cm的长方体木块的棱爬行。如果8个顶点都要经过,那么这只蚂蚁最短的爬行路程是( )cm。
A.92 B.56 C.49 D.46
5.一个正方体相对的面分别是1点和2点、3点和4点、5点和6点。游戏规则:在方格棋盘上沿棱按照箭头方向翻动正方体,每次不能后退。开始时正方体如左图那样摆放,最后翻动到如右图所示的位置,此时正方体朝上的点数是( )。
A.6 B.5 C.3 D.4
6.魔方又叫鲁比克方块,是一款风靡全球的机械益智玩具。辰辰是魔方爱好者,他有一款三阶魔方,即3×3×3。可是,他在一次玩耍中不小心掉了一个小正方体,请问魔方的表面积会( )。
A.变大 B.变小 C.不变 D.答案不唯一
7.把两个棱长为的正方体拼成一个长方体后,表面积减少了( )。
A.6 B.9 C.12 D.18
8.一个长方体容器从里面量,它的长是8分米,宽是5分米,高是6分米,如果高减少2分米,那么该容器少装水( )升。
A.240 B.96 C.80 D.60
9.冬冬在一个长方体盒子中装了一些棱长为1分米的正方体(如图),这个盒子的容积是( )。
A.11立方分米 B.19立方分米 C.30立方分米 D.无法确定
10.一个长方体的长,宽,高分别是a厘米,b厘米,h厘米,如果高增加2厘米,则其体积增加( )立方厘米。
A.abh B.2ab C.2ah D.ab(h+2)
11.在一个透明的长方体盒子内放置棱长为1cm的小正方体(如图)。这个长方体盒子的表面积是( )cm2。
A.66 B.60 C.33 D.30
12.五年级的同学们准备去郊外春游,老师要求每位同学都要带足够的水。小明的妈妈给他准备了一瓶2升的矿泉水,为了携带方便小明需要把水分装到小瓶中,如果每个小瓶装550毫升,那么他至少需要( )个这样的小瓶。
A.2 B.3 C.4 D.5
二、填空题
13.丽丽要把下面长方体展开图折成长方体。
(1)如果A面在底面,那么( )面在上面。
(2)用胶带沿棱将所有接缝处进行粘合,她至少需要用( )厘米的胶带。(提示:可以先画一画需要粘合的边再填空。)
14.一个正方体的棱长总和是4.8m,它的表面积是( )m2,体积是( )dm3。
15.把棱长为1dm的正方体木块,切成棱长为1cm的小正方体,可以切成( )块。
16.一个长方体木块的长是15cm,宽是10cm,高是8cm。从这个木块的一头切下一个最大的正方体后,剩下部分的表面积是( )cm2,体积是( )cm3。
17.一个正方体,如果高减少3cm,就变成了一个长方体。这时表面积比原来减少60cm2。原来正方体的体积是( )cm3。
18.如图,正方体的棱长是4cm,从它的一个顶点处挖去一个棱长是2cm的小正方体,所剩下的物体的表面积是( )cm2。
19.在一个底面积为34平方分米,高7分米的长方体容器中,倒入4分米深的水。现将一个铁块完全浸没在水中,水面上升2分米。这个铁块的体积是( )立方分米。
三、解答题
20.一个长方体无盖玻璃缸(如下图),长7分米,宽6分米,高4分米,水深2.8分米。
(1)做这个玻璃缸需要多少平方分米玻璃?(不考虑玻璃厚度)
(2)如果把下图左边这块棱长为4分米的正方体铁块竖直放入缸里,缸里的水会溢出多少升?
21.一个容器由一个内空棱长10厘米的正方体和一个内空长20厘米,宽20厘米,高15厘米的长方体组合形成(如图)。正放时(长方体在下面)水深10厘米,倒放时(正方体在下面,放平)水最深处多少厘米?
22.如图1,把一张长方形卡纸折一下,立放在桌子上。底部是一个面积为36平方厘米的正方形,直立部分的长是10厘米。
(1)如果把直立的卡纸作为长方体纸盒的其中两个面,那么长方体纸盒的表面积是多少平方厘米?
(2)在这个长方体纸盒中倒入高为5厘米的牛奶,再将这个长方体盒子平放(如图2)。那么此时牛奶高度是多少厘米?
23.为了喜迎“六一儿童节”,不断丰富孩子们的动手实践能力,5月30日,民二小学开展“创意无限捏出精彩”的捏橡皮泥活动。君君参加这次活动时,将一个棱长是8厘米的正方体橡皮泥改捏成一个长10厘米、宽4厘米的长方体作为自己作品的底座。
(1)捏成的这个长方体底座的高是多少厘米?
(2)君君的作品快要完成时,她决定将长方体底座的各个面涂成红色,需要涂色的面积是多少平方厘米?
24.有一个长方体容器,从里面量得长、宽、高分别为18厘米、12厘米、10厘米,里面有水深9厘米。将一个底面边长是6厘米、高7厘米的长方体铁块(底面是正方形)放入水中,溢出水的体积是多少升?
25.孔明灯是一种古老的手工艺品,相传由三国时期的诸葛亮发明而得名,在古代作为军事用途。涛涛和爸爸一起用一根36分米长的铁丝,做了一个正方体灯笼框架,除了底面外,其他面都要糊上安全阻燃纸,至少需要多少平方分米的安全阻燃纸?这个灯笼的体积是多少立方分米?
26.如图,尽可能多地往收纳盒中放纸巾,你可以放置多少包?
结合生活实际想一想,我( )(填“同意”或“不同意")小凯的想法。如果同意,请你写出理由;如果不同意,尽可能多地往乙收纳盒中放纸巾,你可以放置多少包?写出你的思考过程,可以写一写,画一画。
27.如图,在一个棱长为5分米的正方体上面的正中间向下挖一个棱长为2分米的正方体小洞,接着在小洞的底面正中间再向下挖一个棱长为1分米的正方体小洞。求挖洞后的几何体的表面积是多少平方分米?
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D A D D C C B
题号 11 12
答案 A C
1.B
【分析】根据长方体表面积的意义可知,把3盒这样的饼干包装成一件礼品,要使需要的包装纸最少,也就是把饼干盒的最大面重合摞起来,拼成一个长3cm,宽2cm,高cm的长方体,根据长方体的表面积公式:,把数据代入公式解答。
【详解】(cm)
(cm2)
需要包装纸42cm2。
故答案为:B
2.C
【分析】根据圆柱、长方体、正方体的体积公式:V=Sh,圆锥的体积公式:V=Sh,据此解答即可。
【详解】
A.是正方体,能用“底面积×高”求体积;
B.可以看作一个长方体减去半个圆柱体的组合图形,能用“底面积×高”求体积;
C.不能用“底面积×高”求体积;
D.由一个长方体和一个正方体组成,能用“底面积×高”求体积。
故答案为:C
3.D
【分析】根据正方体体积=棱长×棱长×棱长,求出液体体积,再根据长方体的高=体积÷底面积,求出横放时液体高即可。
【详解】8×8×8÷(10×8)
=512÷80
=6.4(cm)
故答案为:D
【点睛】关键是掌握并灵活运用长方体和正方体体积公式。
4.D
【分析】长方体有12条棱,8个顶点。一只蚂蚁沿长方体木块的棱爬行,8个顶点都要经过,要想爬行路程最短,就不要爬重复的路线,尽量爬较短的棱。沿着长方体的一个面的棱爬行,只要爬3条棱就可经过4个顶点,这3条棱最短是5+5+8=18cm,这个面即左(或右)面。因此这一只蚂蚁可以沿长方体木块右面的一个顶点开始爬3条棱即18cm,再经过一条长(10cm)爬到左面,再爬3条棱即18cm,就是最短路程。
【详解】根据分析作最短的爬行路线图如下:
5×4+8×2+10
=20+16+10
=46(cm)
那么这只蚂蚁最短的爬行路程是46cm。
故答案为:D
5.A
【分析】根据箭头从左图的位置翻动到右图的位置,先向上翻动1次,再向右翻动2次:向上翻动1次,5点朝上,向右翻动第1次后,2点朝上,再向右翻动1次,6点朝上。所以此时正方体朝上的点数是6。
【详解】由分析可知:
开始时正方体如左图那样摆放,最后翻动到如右图所示的位置,此时正方体朝上的点数是6。
故答案为:A
6.D
【分析】掉了一个小正方体后,由于掉的小正方体原来的位置不同,魔方的表面积会有不同的变化,需要分类讨论。讨论时,先分析增加的部分,再分析减少的部分,最后对比出魔方的表面积是增还是减。
【详解】①掉的小正方体是魔方的8个顶点中的一处,会减少三个小正方形的面积,同时会增加三个小正方形的面积,那么魔方的表面积不变;
②掉的小正方体是魔方每条棱上非顶点位置的一处,会减少2个小正方形的面积,但同时会增加4个小正方形的面积,那么魔方的表面积变大;
③掉的小正方体在魔方每个面的中心位置,会减少1个小正方形的面积,但同时会增加5个小正方形的面积,那么魔方的表面积变大。
综上可知,魔方的表面积可能变大也可能不变,那么答案不唯一。
故答案为:D
7.D
【分析】由题意可知,表面积减少的是正方体的两个面,根据,代入数据求出正方形的面积再乘2即可得解。
【详解】
(cm2)
把两个棱长为的正方体拼成一个长方体后,表面积减少了18。
故答案为:D
8.C
【分析】根据长方体的体积(容积)=长×宽×高,代入数据计算,求出高减少的2分米的空间的大小即可,最后根据1立方分米=1升,将结果换算成升即可。
【详解】8×5×2=80(立方分米)
80立方分米=80升
该容器少装水80升。
故答案为:C
9.C
【分析】根据图可知,长方体盒子的长等于1×5=5分米,宽等于1×3=3分米,高等于1×2=2分米;根据长方体容积公式:体积=长×宽×高,代入数据,即可解答。
【详解】盒子长:1×5=5(分米)
盒子宽:1×3=3(分米)
盒子高:1×2=2(分米)
盒子容积:
5×3×2
=15×2
=30(立方分米)
冬冬在一个长方体盒子中装了一些棱长为1分米的正方体,这个盒子的容积是30立方分米。
故答案为:C
10.B
【分析】如果高增加2厘米,则其增加的体积等于长a厘米、宽b厘米、高2厘米的长方体的体积,根据长方体的体积=长×宽×高,代入数据计算即可解答。
【详解】a×b×2=2ab(立方厘米)
所以一个长方体的长,宽,高分别是a厘米,b厘米,h厘米,如果高增加2厘米,则其体积增加2ab立方厘米。
故答案为:B
11.A
【分析】根据图可知,这个长方体盒子的长等于4个小正方体的棱长和,宽等于3个小正方体的棱长和,高等于3个小正方体的棱长和,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】长:1×4=4(cm),宽:1×3=3(cm);高:1×3=3(cm)。
表面积:
(4×3+4×3+3×3)×2
=(12+12+9)×2
=(24+9)×2
=33×2
=66(cm2)
在一个透明的长方体盒子内放置棱长为1cm的小正方体(如图)。这个长方体盒子的表面积是66cm2。
故答案为:A
12.C
【分析】先将2升换算成2000毫升,再算2000毫升里有多少个550毫升,就需要多少个这样的瓶,所以用2000÷550=3(个)……350(毫升),要全部装完,不管余下多少,也要一个瓶装,因此至少需要3+1=4(个)瓶。据此解答。
【详解】2升=2000毫升
2000÷550=3(个)……350(毫升)
3+1=4(个)
那么他至少需要4个这样的小瓶。
故答案为:C
13.(1)E
(2)66
【分析】(1)根据长方体的特征,相对的面完全相同,据此解答即可;
(2)由题意可知,需要胶带的长度就是长方体所有接缝处的棱长总和。根据题干展开图可得,接缝处的棱长共有4条高、2条长和1条宽,据此进行计算即可。
【详解】(1)如果A面在底面,那么E面在上面。
(2)7×4+14×2+10
=28+28+10
=66(厘米)
则她至少需要用66厘米的胶带。
14. 0.96 64
【分析】正方体的棱长总和除以12求出它的棱长,再根据正方体的表面积=棱长×棱长×6,求出它的表面积,根据正方体的体积=棱长×棱长×棱长,求出它的体积。注意最后要换算单位,高级单位转化为低级单位乘两个单位之间的进率,1m3=1000dm3。
【详解】4.8÷12=0.4(m)
0.4×0.4×6=0.96(m2)
0.4×0.4×0.4=0.064(m3)
0.064m3=64dm3
则它的表面积是0.96m2,体积是64dm3。
15.1000
【分析】根据1dm=10cm,再根据正方体的体积公式:棱长×棱长×棱长,把数代入分别求出正方体木块和小正方体木块的体积,之后用正方体木块的体积除以小正方体木块的体积即可求出可以切成多少块。
【详解】1dm=10cm
10×10×10÷(1×1×1)
=1000÷1
=1000(块)
可以切成1000块。
16. 572 688
【分析】分析题目,从这个长方体木头上切下一个最大的正方体,则正方体的棱长就等于长方体最短的一条棱,即正方体的棱长是8cm,剩下部分的表面积等于原来长方体的表面积减去棱长是8cm的正方体的2个面的面积,剩下部分的体积等于原来长方体的体积减去切下的正方体的体积,据此根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的表面积=棱长×棱长×6,长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长代入数据列式计算即可。
【详解】(15×10+15×8+10×8)×2-8×8×2
=(150+120+80)×2-64×2
=350×2-128
=700-128
=572(cm2)
15×10×8-8×8×8
=150×8-64×8
=1200-512
=688(cm3)
一个长方体木块的长是15cm,宽是10cm,高是8cm。从这个木块的一头切下一个最大的正方体后,剩下部分的表面积是572cm2,体积是688cm3。
17.125
【分析】分析题目,如果正方体的高减少3cm,则表面积就减少了4个相同的长方形的面,这个长方形的长是正方体的棱长、宽是3cm,据此先用60除以4求出一个面的面积,再除以3即可求出正方体的棱长,最后根据正方体的体积=棱长×棱长×棱长,代入数据计算即可。
【详解】60÷4=15(cm2)
15÷3=5(cm)
5×5×5
=25×5
=125(cm3)
因此,这个正方体的体积是125cm3。
18.96
【分析】分析题目,剩下物体的表面积等于棱长是4cm的正方体的表面积,据此结合正方体的表面积=棱长×棱长×6列式计算即可。
【详解】4×4×6
=16×6
=96(cm2)
正方体的棱长是4cm,从它的一个顶点处挖去一个棱长是2cm的小正方体,所剩下的物体的表面积是96cm2。
19.68
【分析】根据题意可知,物体的体积等于上升部分水的体积,上升部分水的体积等于容器的底面积乘上升部分水的高度,已知长方体容器底面积是34平方分米,上升了2分米,代入数据解答即可求出铁块的体积。
【详解】34×2=68(立方分米)
这个铁块的体积是68立方分米。
20.(1)146平方分米;(2)13.6升
【分析】(1)无盖的长方体表面积只有5个面的面积,也就是无盖长方体的表面积=长×宽+长×高×2+宽×高×2,代入数据即可求出做这个玻璃缸需要多少平方分米玻璃;
(2)根据题意可知,正方体的体积+水的体积=长方体无盖玻璃缸的容积+溢出水的体积,根据正方体的体积=棱长×棱长×棱长以及长方体的体积(容积)=长×宽×高,分别求出对应的体积,进而求出溢出水的体积,再把单位换算成升。
【详解】(1)7×6+7×4×2+6×4×2
=42+56+48
=146(平方分米)
答:做这个玻璃缸需要146平方分米玻璃。
(2)4×4×4=64(立方分米)
7×6×2.8=117.6(立方分米)
7×6×4=168(立方分米)
64+117.6-168=13.6(立方分米)
13.6立方分米=13.6升
答:缸里的水会溢出13.6升。
21.17.5厘米
【分析】根据长方体的体积公式:V=长×宽×高计算出水的容积,根据倒置后水的容积不变计算水深即可。先判断出水的容积大于正方体的体积,则水深超过正方体的棱长,在长方体还有一部分水深。用水的容积减去正方体的体积,求出在长方体里面的水的容积,再除以长方体的底面积,即可求出此时长方体中的水深。用正方体的棱长加上此时长方体中的水深,求出水的总深度。
【详解】20×20×10
=400×10
=4000(立方厘米)
10×10×10
=100×10
=1000(立方厘米)
4000-1000=3000(立方厘米)
3000÷(20×20)
=3000÷400
=7.5(厘米)
10+7.5=17.5(厘米)
答:倒放时(正方体在下面,放平)水最深处17.5厘米。
22.(1)312平方厘米
(2)3厘米
【分析】(1)根据长方体的特征可知,长方体有两个面是正方形,那么其他四个侧面是完全相同的长方形。已知这个长方体的底面是面积为36平方厘米的正方形,根据正方形的面积=边长×边长,可知正方形的边长是6厘米,即长方体的长、宽都是6厘米;那么4个侧面都是“10×6”的长方形,根据长方形的面积=长×宽,求出侧面积,再加上2个正方形的面积,即是这个长方体纸盒的表面积。
(2)在这个长方体纸盒中倒入高为5厘米的牛奶,根据长方体的体积=底面积×高,求出牛奶的体积;再将这个长方体盒子平放,即长方体的底面变成“10×6”的长方形,根据长方体的高=体积÷底面积,即可求出此时牛奶的高度。
【详解】(1)因为36=6×6,所以正方形的边长是6厘米。
36×2+10×6×4
=72+240
=312(平方厘米)
答:长方体纸盒的表面积是312平方厘米。
(2)36×5=180(立方厘米)
180÷(10×6)
=180÷60
=3(厘米)
答:此时牛奶高度是3厘米。
23.(1)12.8厘米
(2)438.4平方厘米
【分析】(1)根据体积的意义可知,把正方体橡皮泥捏成长方体后体积不变,正方体的体积公式:正方体的体积=棱长×棱长×棱长,根据长方体的体积=长×宽 ×高可知长方体的高=体积÷(长×宽),据此代入数据计算即可;
(2)根据长方体的表面积公式:长方体的表面积=(长×宽+长×高+宽×高)×2,把数据代入公式解答即可。
【详解】(1)8×8×8÷(10×4)
=64×8÷40
=512÷40
=12.8(厘米)
答:捏成的这个长方体底座的高是12.8厘米。
(2)(10×4+10×12.8+4×12.8)×2
=(40+128+51.2)×2
=219.2×2
=438.4(平方厘米)
答:需要涂色的面积是438.4平方厘米。
24.0.036升
【分析】长方体的体积(容积)=长×宽×高,溢出水的体积=容器中水的体积+长方体铁块的体积-长方体容器的容积,最后根据“1升=1000立方厘米”把单位转化为“升”,据此解答。
【详解】18×12×9+6×6×7-18×12×10
=216×9+36×7-216×10
=1944+252-2160
=2196-2160
=36(立方厘米)
36立方厘米=0.036升
答:溢出水的体积是0.036升。
25.45平方分米;27立方分米
【分析】由正方体的棱长和=棱长×12可推导出,棱长=正方体的棱长和÷12,据此先用铁丝长度除以12求出正方体灯笼的棱长;正方体灯笼5个面要糊上安全阻燃纸,再用棱长×棱长×5即可求出安全阻燃纸的面积;最后根据正方体的体积=棱长×棱长×棱长,求出这个灯笼的体积。
【详解】(分米)
(平方分米)
(立方分米)
答:至少需要45平方分米的安全阻燃纸。这个灯笼的体积是27立方分米。
26.不同意;7包
【分析】联系生活实际可知,纸巾的形状是固定的有可能收纳盒的容积够,但是纸巾装不下,所以不能直接用收纳盒的容积除以每包纸巾的体积,应该计算收纳盒内部的长对应能放几包,内部的宽对应能放几包,最多能放几层,据此解答即可。
【详解】我不同意小凯的想法。
15÷5=3(包)
17-7=10(厘米)
10÷5=2(包)
15÷7=2(包)……1(厘米)
因为3<4,所以只能放一层纸巾,共可以放置的数量为:
2×2+3
=4+3
=7(包)
如下图所示:
答:最多可以放置7包。
27.170平方分米
【分析】分析题目,通过平移可知:这个图形的表面积就等于棱长是5分米的正方体的表面积加棱长是1分米的正方体的前后左右4个面加棱长是2分米的正方体的前后左右4个面,据此结合正方体的表面积=棱长×棱长×6列式计算即可。
【详解】5×5×6+1×1×4+2×2×4
=25×6+1×4+4×4
=150+4+16
=170(平方分米)
答:挖洞后的几何体的表面积是170平方分米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
