6.1.1 空间向量的线性运算 练习(含详解)2024-2025学年高二数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 6.1.1 空间向量的线性运算 练习(含详解)2024-2025学年高二数学苏教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-18 16:38:59 | ||
图片预览

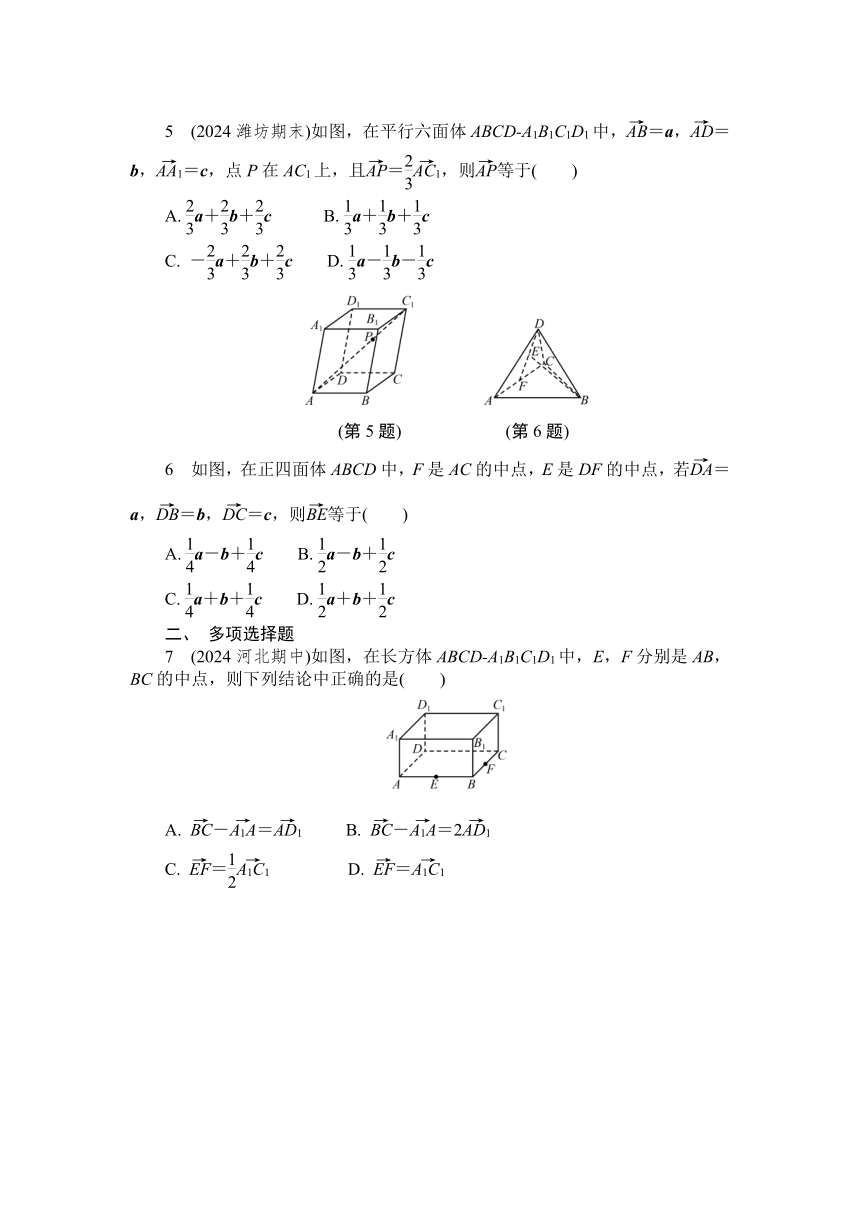

文档简介
6.1.1 空间向量的线性运算
一、 单项选择题
1 如图,在四棱柱的上底面ABCD中,=,则下列向量中相等的是( )
A. 与 B. 与
C. 与 D. 与
(第1题) (第4题)
2 (2024云浮月考)已知空间中不共线的向量a,b,且=a+2b,=-5a+6b,=7a-2b,则一定共线的三点是( )
A. A,B,C B. B,C,D
C. A,B,D D. A,C,D
3 (2023威海期末)在平行六面体ABCD-A1B1C1D1中,点E满足=-++,则下列选项中正确的是( )
A. 3= B. 3=2
C. =3 D. 2=3
4 (2023衡阳期末)如图,在四面体PABC中,E是AC的中点,=3,设=a,=b,=c,则 等于( )
A. a-b+c B. a-b+c
C. a+b+c D. a-b+c
5 (2024潍坊期末)如图,在平行六面体ABCD-A1B1C1D1中,=a,=b,=c,点P在AC1上,且=,则等于( )
A. a+b+c B. a+b+c
C. -a+b+c D. a-b-c
(第5题) (第6题)
6 如图,在正四面体ABCD中,F是AC的中点,E是DF的中点,若=a,=b,=c,则等于( )
A. a-b+c B. a-b+c
C. a+b+c D. a+b+c
二、 多项选择题
7 (2024河北期中)如图,在长方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点,则下列结论中正确的是( )
A. -= B. -=2
C. = D. =
8 (2024武汉期中)如图,在空间四边形OABC中,M,N分别是边OA,CB上的点,且AM=2MO,CN=2NB,G是线段MN的中点,则下列向量表示正确的是( )
A. =-++
B. =-+
C. =+-
D. =++
三、 填空题
9 (2024济南期末)如图,在三棱柱ABC-A1B1C1中,若=a,=b,=c,则用a,b,c表示=________.
10 (2024江苏月考)若空间非零向量e1,e2不共线,则使2ke1-e2与e1+2(k+1)e2共线的k的值为________.
11 在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=m+n,其中m=1,n∈[0,1],则△AB1P周长的最小值是________.
四、 解答题
12 如图,在长方体ABCD-A1B1C1D1中,M是对角线AC1的中点,化简下列表达式:
(1) ++;
(2) +-.
13 证明:若坐标平面内的三点A,B,C共线,O为坐标原点,则存在三个均不为零的实数l,m,n,使得l+m+n=0,且l+m+n=0,反之也成立.
6.1.1 空间向量的线性运算
1. D 由题意,得四边形ABCD是平行四边形.对于A, 与的方向相反,不是相等向量,故A错误;对于B, 与的方向相反,不是相等向量,故B错误;对于C, 与的方向不同,不是相等向量,故C错误;对于D, 与的方向相同,大小相等,属于相等向量,故D正确.
2. C 对于A,因为=+=-4a+8b,所以不存在任何λ∈R,使得=λ,所以A,B,C三点不共线,故A错误;对于B,因为=+=2a+4b,所以不存在任何μ∈R,使得=μ,所以B,C,D三点不共线,故B错误;对于C,因为=++=3a+6b,所以=3,所以A,B,D三点共线,故C正确;对于D,因为=+=-4a+8b,所以不存在任何t∈R,使得=t,所以A,C,D三点不共线,故D错误.
3. A 由=-++,得-=-(-)-+(-),整理,得3=-==.
4. B 由题意,得=-=(+)-=a-b+c.
5. A 在平行六面体ABCD-A1B1C1D1中,=++=++.因为=a,=b,=c,点P在AC1上,且=,所以=(++)=a+b+c.
6. A 由题意,得=+=-+=-+×(+)=-+=a-b+c.
7. AC -=+=,故A正确,B错误;=,故C正确,D错误.故选AC.
8. CD 在空间四边形OABC中,=2,=2,G是线段MN的中点,=+=+=+(-)=+,=(+)=×+(+)=++,故D正确;对于A,=-=++-=-++,故A错误;对于B,=-=++-=-+,故B错误;对于C,=-=++-=+-,故C正确.故选CD.
9. -a+b+c 由题意,得=+=+-=-a+b+c.
10. - 由题意,得存在实数λ使得2ke1-e2=λ[e1+2(k+1)e2]=λe1+2λ(k+1)e2,即解得
11. + 因为=m+n=m+n,其中m=1,n∈[0,1],所以点P在线段CC1上.如图所示,沿AA1展开正三棱柱ABC-A1B1C1的侧面,故△AB1P的周长为AB1+AP+B1P=+AP+B1P≥+=+,当B1,P,A三点共线时,取等号.
12. (1) ++=+=.
(2) +-=(+)-=-=+=+==.
13. ①若l+m+n=0(l,m,n均不为0),
则--=1,
所以-=1+.
又l+m+n=0,
所以=--=(1+)-=+(-)=-,
所以-=-,
所以=-,
所以A,B,C三点共线.
②若A,B,C三点共线,则存在常数λ,
使=λ(λ≠0 且λ≠1),
所以-=λ(-),
所以+(λ-1)-λ=0.
令l=1,m=λ-1,n=-λ,
则由λ≠0且λ≠1,知l,m,n,不为零,
所以l+m+n=0,
且l+m+n=0.
一、 单项选择题
1 如图,在四棱柱的上底面ABCD中,=,则下列向量中相等的是( )
A. 与 B. 与
C. 与 D. 与
(第1题) (第4题)
2 (2024云浮月考)已知空间中不共线的向量a,b,且=a+2b,=-5a+6b,=7a-2b,则一定共线的三点是( )
A. A,B,C B. B,C,D
C. A,B,D D. A,C,D
3 (2023威海期末)在平行六面体ABCD-A1B1C1D1中,点E满足=-++,则下列选项中正确的是( )
A. 3= B. 3=2
C. =3 D. 2=3
4 (2023衡阳期末)如图,在四面体PABC中,E是AC的中点,=3,设=a,=b,=c,则 等于( )
A. a-b+c B. a-b+c
C. a+b+c D. a-b+c
5 (2024潍坊期末)如图,在平行六面体ABCD-A1B1C1D1中,=a,=b,=c,点P在AC1上,且=,则等于( )
A. a+b+c B. a+b+c
C. -a+b+c D. a-b-c
(第5题) (第6题)
6 如图,在正四面体ABCD中,F是AC的中点,E是DF的中点,若=a,=b,=c,则等于( )
A. a-b+c B. a-b+c
C. a+b+c D. a+b+c
二、 多项选择题
7 (2024河北期中)如图,在长方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点,则下列结论中正确的是( )
A. -= B. -=2
C. = D. =
8 (2024武汉期中)如图,在空间四边形OABC中,M,N分别是边OA,CB上的点,且AM=2MO,CN=2NB,G是线段MN的中点,则下列向量表示正确的是( )
A. =-++
B. =-+
C. =+-
D. =++
三、 填空题
9 (2024济南期末)如图,在三棱柱ABC-A1B1C1中,若=a,=b,=c,则用a,b,c表示=________.
10 (2024江苏月考)若空间非零向量e1,e2不共线,则使2ke1-e2与e1+2(k+1)e2共线的k的值为________.
11 在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=m+n,其中m=1,n∈[0,1],则△AB1P周长的最小值是________.
四、 解答题
12 如图,在长方体ABCD-A1B1C1D1中,M是对角线AC1的中点,化简下列表达式:
(1) ++;
(2) +-.
13 证明:若坐标平面内的三点A,B,C共线,O为坐标原点,则存在三个均不为零的实数l,m,n,使得l+m+n=0,且l+m+n=0,反之也成立.
6.1.1 空间向量的线性运算
1. D 由题意,得四边形ABCD是平行四边形.对于A, 与的方向相反,不是相等向量,故A错误;对于B, 与的方向相反,不是相等向量,故B错误;对于C, 与的方向不同,不是相等向量,故C错误;对于D, 与的方向相同,大小相等,属于相等向量,故D正确.
2. C 对于A,因为=+=-4a+8b,所以不存在任何λ∈R,使得=λ,所以A,B,C三点不共线,故A错误;对于B,因为=+=2a+4b,所以不存在任何μ∈R,使得=μ,所以B,C,D三点不共线,故B错误;对于C,因为=++=3a+6b,所以=3,所以A,B,D三点共线,故C正确;对于D,因为=+=-4a+8b,所以不存在任何t∈R,使得=t,所以A,C,D三点不共线,故D错误.
3. A 由=-++,得-=-(-)-+(-),整理,得3=-==.
4. B 由题意,得=-=(+)-=a-b+c.
5. A 在平行六面体ABCD-A1B1C1D1中,=++=++.因为=a,=b,=c,点P在AC1上,且=,所以=(++)=a+b+c.
6. A 由题意,得=+=-+=-+×(+)=-+=a-b+c.
7. AC -=+=,故A正确,B错误;=,故C正确,D错误.故选AC.
8. CD 在空间四边形OABC中,=2,=2,G是线段MN的中点,=+=+=+(-)=+,=(+)=×+(+)=++,故D正确;对于A,=-=++-=-++,故A错误;对于B,=-=++-=-+,故B错误;对于C,=-=++-=+-,故C正确.故选CD.
9. -a+b+c 由题意,得=+=+-=-a+b+c.
10. - 由题意,得存在实数λ使得2ke1-e2=λ[e1+2(k+1)e2]=λe1+2λ(k+1)e2,即解得
11. + 因为=m+n=m+n,其中m=1,n∈[0,1],所以点P在线段CC1上.如图所示,沿AA1展开正三棱柱ABC-A1B1C1的侧面,故△AB1P的周长为AB1+AP+B1P=+AP+B1P≥+=+,当B1,P,A三点共线时,取等号.
12. (1) ++=+=.
(2) +-=(+)-=-=+=+==.
13. ①若l+m+n=0(l,m,n均不为0),
则--=1,
所以-=1+.
又l+m+n=0,
所以=--=(1+)-=+(-)=-,
所以-=-,
所以=-,
所以A,B,C三点共线.
②若A,B,C三点共线,则存在常数λ,
使=λ(λ≠0 且λ≠1),
所以-=λ(-),
所以+(λ-1)-λ=0.
令l=1,m=λ-1,n=-λ,
则由λ≠0且λ≠1,知l,m,n,不为零,
所以l+m+n=0,
且l+m+n=0.
