6.3.2 空间线面关系的判定 练习(2课时,含详解)2024-2025学年高二数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 6.3.2 空间线面关系的判定 练习(2课时,含详解)2024-2025学年高二数学苏教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 479.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-18 16:45:54 | ||
图片预览




文档简介
6.3.2 空间线面关系的判定(1)
一、 单项选择题
1 (2024茂名期末)已知直线l的方向向量为m=(a,1,-2),平面α的一个法向量为n=(-1,2,3),若直线l∥平面α,则实数a的值为( )
A. -7 B. 2 C. -1 D. -4
2 (2024重庆黔江月考)已知平面α的一个法向量为(1,-2,-1),平面β的一个法向量为(-1,2,k).若α∥β,则实数k的值为( )
A. -2 B. -1 C. 1 D. 2
3 (2024深圳期末)已知空间中两条不同的直线m,n,其方向向量分别为a,b,则“a,b共线”是“直线m,n平行”的( )
A. 充分且不必要条件
B. 必要且不充分条件
C. 充要条件
D. 既不充分又不必要条件
4 在长方体ABCDA1B1C1D1中,E是BB1的中点,=λ,且EF∥平面ACD1,则实数λ的值为( )
A. B.
C. D.
5 (2024广州期中)已知e1,e2,e3为空间内三个不共面的向量,平面α和平面β的法向量分别为a=e1+λe2+3e3和b=-e1+2e2+μe3,若α∥β,则λ+μ的值为( )
A. 5 B. -5 C. 3 D. -3
6 (2024台州期中)如图,在长方体ABCDA1B1C1D1中,AD=AA1=3,AB=4,E,F,G分别是棱C1D1,BC,CC1的中点,M是矩形ABCD内一动点(不含边界),若直线D1M与平面EFG平行,则·的最小值为( )
A. 2 B. 9 C. D.
二、 多项选择题
7 (2024永州期末)已知平面α与平面β平行,若平面α的一个法向量为n=(-1,2,-3),则平面β的法向量可以是( )
A. (1,-2,3) B. (-1,-2,3)
C. (2,-4,6) D. (2,-4,-6)
8 在正方体ABCDA1B1C1D1中,E为AA1的中点,若直线EF∥平面A1BC1,则点F的位置可能是( )
A. 线段CC1的中点
B. 线段BC的中点
C. 线段CD的中点
D. 线段C1D1的中点
三、 填空题
9 已知两个不重合的平面α与平面ABC,若平面α的一个法向量为n1=(2,-3,1),=(1,0,-2),=(1,1,1),则平面α与平面ABC的位置关系是________.
10 若平面α的一个法向量为u1=(-3,y,2),平面β的一个法向量为u2=(6,-2,z),且α∥β,则y=________,z=________.
11 (2024聊城期中)如图,PA⊥平面ABCD,四边形ABCD是正方形,E,F分别为PD,PB的中点,点G在线段AP上,AC与BD交于点O,PA=AB=2,若OG∥平面EFC,则AG=________.
四、 解答题
12 如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4,E为棱PD的中点,=λ(λ为常数,且0<λ<1).若直线BF∥平面ACE,求实数λ的值.
13 (2024株洲期中)如图,已知在正方体ABCDA1B1C1D1中,M,N,P分别是AD1,BD,B1C的中点.证明:
(1) MN∥平面CC1D1D;
(2) 平面MNP∥平面CC1D1D.
6.3.2 空间线面关系的判定(2)
一、 单项选择题
1 (2024菏泽期末)已知n1=(,x,2),n2=(-3,,-2)分别是平面α,β的法向量,若α⊥β,则实数x的值为( )
A. -7 B. -1
C. 1 D. 7
2 已知点A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
A. 直角三角形
B. 等腰三角形
C. 等边三角形
D. 等腰直角三角形
3 (2024盐城期中)设m为实数,若直线l垂直于平面α,且l的一个方向向量为(m,2,4),平面α的一个法向量为(2,4,8),则m的值为( )
A. 1 B. 2
C. -20 D. -10
4 (2024长沙月考)如图,在正方体ABCDA1B1C1D1中,M,N分别是棱DD1和线段BC1上的动点,则满足与AD1垂直的直线MN( )
A. 有且仅有1条
B. 有且仅有2条
C. 有且仅有3条
D. 有无数条
5 (2024扬州月考)已知正方体ABCDA1B1C1D1的棱长为1,动点M在线段CC1上,动点P在平面A1B1C1D1上,且AP⊥平面MBD1,则线段BP长度的取值范围是( )
A. [1,] B. [,]
C. [,] D. [1,]
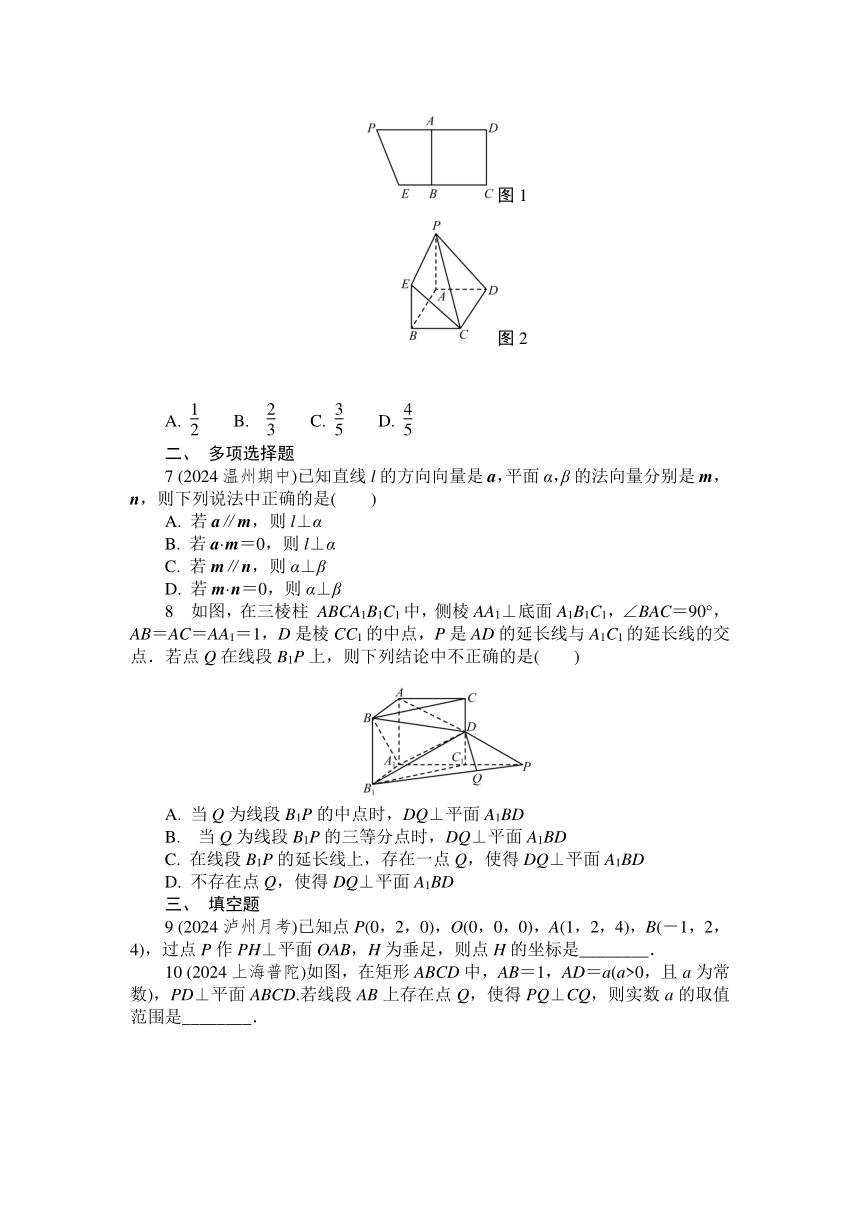
6 如图1,在梯形CEPD中,PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,如图2.已知当点F满足=λ(0<λ<1)时,平面DEF⊥平面PCE,则实数λ的值为( )
图1
图2
A. B. C. D.
二、 多项选择题
7 (2024温州期中)已知直线l的方向向量是a,平面α,β的法向量分别是m,n,则下列说法中正确的是( )
A. 若a∥m,则l⊥α
B. 若a·m=0,则l⊥α
C. 若m∥n,则α⊥β
D. 若m·n=0,则α⊥β
8 如图,在三棱柱 ABCA1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.若点Q在线段B1P上,则下列结论中不正确的是( )
A. 当Q为线段B1P的中点时,DQ⊥平面A1BD
B. 当Q为线段B1P的三等分点时,DQ⊥平面A1BD
C. 在线段B1P的延长线上,存在一点Q,使得DQ⊥平面A1BD
D. 不存在点Q,使得DQ⊥平面A1BD
三、 填空题
9 (2024泸州月考)已知点P(0,2,0),O(0,0,0),A(1,2,4),B(-1,2,4),过点P作PH⊥平面OAB,H为垂足,则点H的坐标是________.
10 (2024上海普陀)如图,在矩形ABCD中,AB=1,AD=a(a>0,且a为常数),PD⊥平面ABCD.若线段AB上存在点Q,使得PQ⊥CQ,则实数a的取值范围是________.
11 已知正方体ABCDA1B1C1D1的棱长为1,点M在线段CC1上,且=2.点P在平面A1B1C1D1上,且AP⊥平面MBD1,则线段AP的长为________.
四、 解答题
12 (2024山东月考)如图,已知在直三棱柱ABCFGE中,AC=BC=4,AC⊥BC,O为BC的中点,D为侧棱BG上一点,且BD=BG,三棱柱ABCFGE的体积为32.过点O作OQ⊥DE,垂足为Q.求证:BQ⊥平面ACQ.
13 (2024广东月考)如图,在四棱锥PABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3,E为PD的中点,点F在PC上,且=.求证:平面AEF⊥平面PCD.
6.3.2 空间线面关系的判定(1)
1. D 由直线l∥平面α,得m⊥n,则m·n=-a+2-6=0,所以a=-4.
2. C 因为平面α的一个法向量为(1,-2,-1),平面β的一个法向量为(-1,2,k),且α∥β,所以==,解得k=1.
3. C 若直线的方向向量a,b共线,则两直线平行或重合.又直线m,n是空间中两条不同的直线,所以两直线m,n平行,即“a,b共线”是“直线m,n平行”的充分条件;若直线m,n平行,则a,b共线,即“a,b共线”是“直线m,n平行”的必要条件.综上,“a,b共线”是“直线m,n平行”的充要条件.
4. B 建立如图所示的空间直角坐标系,设DA=a,DC=b,DD1=c,则A(a,0,0),C(0,b,0),D1(0,0,c),E(a,b,),B1(a,b,c),所以=(-a,b,0),=(-a,0,c),=(-a,-b,0).因为=λ,所以=(-λa,-λb,0),所以F((1-λ)a,(1-λ)b,c),所以=(-λa,-λb,).设平面ACD1的法向量为n=(x,y,z),则取x=bc,则y=ac,z=ab,所以n=(bc,ac,ab).因为EF∥平面ACD1,所以⊥n,所以·n=-λabc-λabc+=0,解得λ=.
5. B 因为e1,e2,e3为空间内三个不共面的向量,所以e1,e2,e3可以作为空间内的一个基底.又平面α和平面β的法向量分别为a=e1+λe2+3e3和b=-e1+2e2+μe3,且α∥β,所以a∥b,则a=tb,即e1+λe2+3e3=t(-e1+2e2+μe3),所以解得所以λ+μ=-5.
6. C 分别以,,的方向为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,则E(2,3,3),F(4,,0),G(4,3,),D1(0,3,3),B1(4,0,3),M(x,y,0),=(2,-,-3),=(0,,),=(x,y-3,-3).设平面EFG的法向量n=(x1,y1,z1),则得令y1=1,则n=(-,1,-1).由于直线D1M与平面EFG平行,故·n=0,则-x+y-3+3=0,即y=x.因为=(4-x,-y,3),=(-x,3-y,3),所以·=(4-x)·(-x)+(-y)·(3-y)+9=x2-4x+y2-3y+9=x2-4x+(x)2-+9=x2-x+9=(x-2)2+,由于x∈(0,4),故当x=2时,·取得最小值,最小值为.
7. AC 因为平面α与平面β平行,所以平面α的法向量与平面β的法向量平行.对于A,若(1,-2,3)=λ(-1,2,-3),则此时λ=-1,满足平面α的法向量与平面β的法向量平行,故A正确;对于B,若(-1,-2,3)=λ(-1,2,-3),则此时无解,不满足平面α的法向量与平面β的法向量平行,故B错误;对于C,若(2,-4,6)=λ(-1,2,-3),则此时λ=-2,满足平面α的法向量与平面β的法向量平行,故C正确;对于D,若(2,-4,-6)=λ(-1,2,-3),则此时无解,不满足平面α的法向量与平面β的法向量平行,故D错误.故选AC.
8. ABD 如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.设CC1,BC,CD,C1D1的中点分别为M,N,P,Q.不妨设棱长为2,则A1(2,0,2),B(2,2,0),C1(0,2,2),E(2,0,1),M(0,2,1),N(1,2,0),P(0,1,0),Q(0,1,2),=(0,2,-2),=(-2,2,0).设平面A1BC1的法向量为n=(x,y,z),则令y=1,则n=(1,1,1).又=(-2,2,0),=(-1,2,-1),=(-2,1,-1),=(-2,1,1),则·n=-2×1+2×1=0,·n=-1×1+2×1-1×1=0,·n=-2×1+1×1-1×1=-2,·n=-2×1+1×1+1×1=0,又EM,EN,EQ均不在平面A1BC1内,所以EM,EN,EQ都平行于平面A1BC1,即若直线EF∥平面A1BC1,则点F的位置可能是线段CC1的中点,线段BC的中点或线段C1D1的中点.故选ABD.
9. 平行 因为平面α的一个法向量为n1=(2,-3,1),=(1,0,-2),=(1,1,1),且n1·=(2,-3,1)·(1,0,-2)=2+0-2=0,所以n1⊥.同理可证n1⊥.又AB∩AC=A,AB 平面ABC,AC 平面ABC,所以n1⊥平面ABC.又n1为平面α的一个法向量,所以平面α∥平面ABC.
10. 1 -4 因为α∥β,所以u1∥u2,所以存在实数λ使得u1=λu2,即(-3,y,2)=λ(6,-2,z),所以解得
11. 以A为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系.由题意,得P(0,0,2),B(2,0,0),D(0,2,0),C(2,2,0),O(1,1,0),F(1,0,1),E(0,1,1),所以=(1,2,-1),=(-1,1,0).设平面EFC的法向量为n=(x,y,z),所以则取x=1,则y=1,z=3,所以n=(1,1,3).因为OG∥平面EFC,所以n·=0.设G(0,0,a),则=(-1,-1,a),所以-1-1+3a=0,解得a=,所以G(0,0,),即AG=.
12. 因为PA⊥底面ABCD,AB 平面ABCD,AD 平面ABCD,所以PA⊥AB,PA⊥AD.
由题意,得AB,AD,AP两两垂直,建立如图所示的空间直角坐标系Oxyz,
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,4,0),P(0,0,2),E(0,2,1),
所以=(2,2,0),=(0,2,1),=(-2,0,2),=(2,2,-2),
则=λ=(2λ,2λ,-2λ),
所以=+=(2λ-2,2λ,2-2λ).
设平面ACE的法向量为m=(x,y,z),
则即
取x=1,所以m=(1,-1,2).
因为BF∥平面ACE,
所以·m=2λ-2-2λ+4-4λ=0,解得λ=.
13. (1) 以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系.
设正方体的棱长为2,则A(2,0,0),C(0,2,0),D(0,0,0),M(1,0,1),N(1,1,0),P(1,2,1).
由正方体的性质知,AD⊥平面CC1D1D,
所以=(2,0,0)为平面CC1D1D的一个法向量.
因为=(0,1,-1),所以·=0×2+1×0+(-1)×0=0,
所以⊥.
又MN 平面CC1D1D,
所以MN∥平面CC1D1D.
(2) 因为=(2,0,0)为平面CC1D1D的一个法向量,且=(0,2,0),=(0,1,-1),
所以
即=(2,0,0)也是平面MNP的一个法向量,
所以平面MNP∥平面CC1D1D.
6.3.2 空间线面关系的判定(2)
1. D 因为α⊥β,所以n1⊥n2,所以n1·n2=×(-3)+x×+2×(-2)=0,解得x=7.
2. A 因为=(5,1,-7),=(2,-3,1),所以·=0,所以⊥,且||≠||,所以△ABC的形状是直角三角形.
3. A 因为直线l垂直于平面α,所以直线l的一个方向向量(m,2,4)与平面α的一个法向量(2,4,8)平行,即==,解得m=1.
4. D 以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,设正方体棱长为1,设M(0,0,a),N(x,1,1-x),则A(1,0,0),D1(0,0,1),所以=(x,1,1-x-a),=(-1,0,1).若AD1⊥MN,则·=-x+1-x-a=0,即2x=1-a(0≤x≤1,0≤a≤1),方程有无数组解.
5. D 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.由正方体ABCDA1B1C1D1的棱长为1,可得A(1,0,0),B(1,1,0),D1(0,0,1).设P(a,b,1),M(0,1,t)(0≤t≤1),则=(a-1,b,1),=(-1,-1,1),=(0,-1,1-t).因为AP⊥平面MBD1,所以AP⊥BD1,AP⊥MD1,即解得所以=(t,1-t,1),所以=+=(0,-1,0)+(t,1-t,1)=(t,-t,1),所以||==.因为0≤t≤1,结合复合函数单调性,得||=在区间[0,1]上单调递增.故||=∈[1,].
6. C 因为四边形ABCD为正方形,且平面PABE⊥平面ABCD,所以PA,AB,AD两两垂直,且PA∥BE,建立如图所示的空间直角坐标系Axyz.因为PD=8,CE=6,所以P(0,0,4),C(4,4,0),E(4,0,2),D(0,4,0),B(4,0,0),则F(4λ,0,0),=(4,-4,2),=(4λ,-4,0),=(0,-4,2),=(-4,0,2).设平面DEF的法向量为m=(x,y,z),则即所以令x=1,则m=(1,λ,2λ-2).设平面PCE的法向量为n=(a,b,c),则即所以令a=1,则n=(1,1,2).因为平面DEF⊥平面PCE,所以m·n=1+λ+2(2λ-2)=5λ-3=0,解得λ=.
7. AD 若a∥m,则l⊥α,故A正确;若a·m=0,则l∥α或l在α内,故B错误;若m∥n,则α∥β,故C错误;若m·n=0,则α⊥β,故D正确.故选AD.
8. ABC 以A1 为坐标原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1),D(0,1,),P(0,2,0),则=(1,0,1),=(0,1,),=(-1,2,0),=(1,-1,-).设平面A1BD的法向量为n=(x,y,z),则取z=-2,则x=2,y=1,所以平面A1BD的一个法向量为n=(2,1,-2).设=λ=λ(-1,2,0)=(-λ,2λ,0),则=+=(1-λ,-1+2λ,-).假设DQ⊥平面A1BD,所以也是平面A1BD的一个法向量,所以n=(2,1,-2)与=(1-λ,-1+2λ,-)共线,则===成立,所以则关于λ的方程组无解,故不存在点Q,使得DQ⊥平面A1BD,故A,B,C错误,D正确.故选ABC.
9. (0,,) 设H(a,b,c),则=(a,b-2,c),=(1,2,4),=(-1,2,4).因为PH⊥平面OAB,OA 平面OAB,OB 平面OAB,所以PH⊥OA,PH⊥OB,则解得a=0,b=2-2c,所以H(0,2-2c,c).因为PH⊥平面OAB,H为垂足,所以O,A,B,H四点共面,则存在唯一实数对(x,y)使得=x+y,即(0,2-2c,c)=(x-y,2x+2y,4x+4y),所以解得x=y=,c=,所以H(0,,).
10. (0,] 因为在矩形ABCD中,AB=1,AD=a,PD⊥平面ABCD,所以以D为坐标原点,DA,DC,DP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设DP=b,AQ=x(00,对称轴方程为x=,则f()=a2-≤0.又因为a>0,所以011. 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),C1(0,1,1).由=2,得M是靠近点C的线段CC1的三等分点,则M(0,1,),所以=(-1,-1,1),=(-1,0,).因为点P在平面A1B1C1D1上,设P(x,y,1),则=(x-1,y,1).由AP⊥平面MBD1,得解得所以=(,,1),||==,即线段AP的长为.
12. 由直三棱柱ABC-FGE,得CE⊥平面ABC.因为AC⊥BC,AC=BC=4,
所以三棱柱ABC-FGE的体积V=AC×BC×CE=×4×4×CE=32,解得EC=4.
因为三棱柱ABC-FGE为直三棱柱,
所以AC⊥CE,BC⊥CE.
因为AC⊥BC,所以CA,CB,CE两两垂直,
以C为坐标原点,CA,CB,CE所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则O(0,2,0),D(0,4,1),E(0,0,4),B(0,4,0),A(4,0,0),C(0,0,0),
则=(0,-4,3).设=λ=(0,-4λ,3λ),则Q(0,4-4λ,1+3λ),
故=(0,2-4λ,1+3λ).
因为OQ⊥DE,所以·=0,
所以0-8+16λ+3+9λ=0,解得λ=,
即Q(0,,),
所以=(0,-,),=(0,,),
所以·=(4,0,0)·(0,-,)=0,
·=(0,,)·(0,-,)=-+=0,
所以BQ⊥CA,BQ⊥CQ.
又CA 平面ACQ,CQ 平面ACQ,CA∩CQ=C,
所以BQ⊥平面ACQ.
13. 如图,以D为坐标原点,DA,DC所在直线分别为x轴,y轴,过点D作AP的平行线为z轴,建立如图所示的空间直角坐标系,则D(0,0,0),A(2,0,0),C(0,2,0),P(2,0,2),E(1,0,1),B(3,2,0),
所以=(0,2,0),=(-2,2,-2).
因为=,所以=,
所以=+=(-2,2,-2)+(2,0,2)=(,,),即F(,,),
所以=(-,,),=(-1,0,1).
设平面AEF的法向量为n=(x,y,z),
则
取x=z=1,则y=-1,所以n=(1,-1,1).
设平面PCD的法向量为m=(a,b,c),
则
取a=1,则c=-1,所以m=(1,0,-1),
所以n·m=1×1+(-1)×0+1×(-1)=0,
所以n⊥m,
所以平面AEF⊥平面PCD.
一、 单项选择题
1 (2024茂名期末)已知直线l的方向向量为m=(a,1,-2),平面α的一个法向量为n=(-1,2,3),若直线l∥平面α,则实数a的值为( )
A. -7 B. 2 C. -1 D. -4
2 (2024重庆黔江月考)已知平面α的一个法向量为(1,-2,-1),平面β的一个法向量为(-1,2,k).若α∥β,则实数k的值为( )
A. -2 B. -1 C. 1 D. 2
3 (2024深圳期末)已知空间中两条不同的直线m,n,其方向向量分别为a,b,则“a,b共线”是“直线m,n平行”的( )
A. 充分且不必要条件
B. 必要且不充分条件
C. 充要条件
D. 既不充分又不必要条件
4 在长方体ABCDA1B1C1D1中,E是BB1的中点,=λ,且EF∥平面ACD1,则实数λ的值为( )
A. B.
C. D.
5 (2024广州期中)已知e1,e2,e3为空间内三个不共面的向量,平面α和平面β的法向量分别为a=e1+λe2+3e3和b=-e1+2e2+μe3,若α∥β,则λ+μ的值为( )
A. 5 B. -5 C. 3 D. -3
6 (2024台州期中)如图,在长方体ABCDA1B1C1D1中,AD=AA1=3,AB=4,E,F,G分别是棱C1D1,BC,CC1的中点,M是矩形ABCD内一动点(不含边界),若直线D1M与平面EFG平行,则·的最小值为( )
A. 2 B. 9 C. D.
二、 多项选择题
7 (2024永州期末)已知平面α与平面β平行,若平面α的一个法向量为n=(-1,2,-3),则平面β的法向量可以是( )
A. (1,-2,3) B. (-1,-2,3)
C. (2,-4,6) D. (2,-4,-6)
8 在正方体ABCDA1B1C1D1中,E为AA1的中点,若直线EF∥平面A1BC1,则点F的位置可能是( )
A. 线段CC1的中点
B. 线段BC的中点
C. 线段CD的中点
D. 线段C1D1的中点
三、 填空题
9 已知两个不重合的平面α与平面ABC,若平面α的一个法向量为n1=(2,-3,1),=(1,0,-2),=(1,1,1),则平面α与平面ABC的位置关系是________.
10 若平面α的一个法向量为u1=(-3,y,2),平面β的一个法向量为u2=(6,-2,z),且α∥β,则y=________,z=________.
11 (2024聊城期中)如图,PA⊥平面ABCD,四边形ABCD是正方形,E,F分别为PD,PB的中点,点G在线段AP上,AC与BD交于点O,PA=AB=2,若OG∥平面EFC,则AG=________.
四、 解答题
12 如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4,E为棱PD的中点,=λ(λ为常数,且0<λ<1).若直线BF∥平面ACE,求实数λ的值.
13 (2024株洲期中)如图,已知在正方体ABCDA1B1C1D1中,M,N,P分别是AD1,BD,B1C的中点.证明:
(1) MN∥平面CC1D1D;
(2) 平面MNP∥平面CC1D1D.
6.3.2 空间线面关系的判定(2)
一、 单项选择题
1 (2024菏泽期末)已知n1=(,x,2),n2=(-3,,-2)分别是平面α,β的法向量,若α⊥β,则实数x的值为( )
A. -7 B. -1
C. 1 D. 7
2 已知点A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
A. 直角三角形
B. 等腰三角形
C. 等边三角形
D. 等腰直角三角形
3 (2024盐城期中)设m为实数,若直线l垂直于平面α,且l的一个方向向量为(m,2,4),平面α的一个法向量为(2,4,8),则m的值为( )
A. 1 B. 2
C. -20 D. -10
4 (2024长沙月考)如图,在正方体ABCDA1B1C1D1中,M,N分别是棱DD1和线段BC1上的动点,则满足与AD1垂直的直线MN( )
A. 有且仅有1条
B. 有且仅有2条
C. 有且仅有3条
D. 有无数条
5 (2024扬州月考)已知正方体ABCDA1B1C1D1的棱长为1,动点M在线段CC1上,动点P在平面A1B1C1D1上,且AP⊥平面MBD1,则线段BP长度的取值范围是( )
A. [1,] B. [,]
C. [,] D. [1,]
6 如图1,在梯形CEPD中,PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,如图2.已知当点F满足=λ(0<λ<1)时,平面DEF⊥平面PCE,则实数λ的值为( )
图1
图2
A. B. C. D.
二、 多项选择题
7 (2024温州期中)已知直线l的方向向量是a,平面α,β的法向量分别是m,n,则下列说法中正确的是( )
A. 若a∥m,则l⊥α
B. 若a·m=0,则l⊥α
C. 若m∥n,则α⊥β
D. 若m·n=0,则α⊥β
8 如图,在三棱柱 ABCA1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.若点Q在线段B1P上,则下列结论中不正确的是( )
A. 当Q为线段B1P的中点时,DQ⊥平面A1BD
B. 当Q为线段B1P的三等分点时,DQ⊥平面A1BD
C. 在线段B1P的延长线上,存在一点Q,使得DQ⊥平面A1BD
D. 不存在点Q,使得DQ⊥平面A1BD
三、 填空题
9 (2024泸州月考)已知点P(0,2,0),O(0,0,0),A(1,2,4),B(-1,2,4),过点P作PH⊥平面OAB,H为垂足,则点H的坐标是________.
10 (2024上海普陀)如图,在矩形ABCD中,AB=1,AD=a(a>0,且a为常数),PD⊥平面ABCD.若线段AB上存在点Q,使得PQ⊥CQ,则实数a的取值范围是________.
11 已知正方体ABCDA1B1C1D1的棱长为1,点M在线段CC1上,且=2.点P在平面A1B1C1D1上,且AP⊥平面MBD1,则线段AP的长为________.
四、 解答题
12 (2024山东月考)如图,已知在直三棱柱ABCFGE中,AC=BC=4,AC⊥BC,O为BC的中点,D为侧棱BG上一点,且BD=BG,三棱柱ABCFGE的体积为32.过点O作OQ⊥DE,垂足为Q.求证:BQ⊥平面ACQ.
13 (2024广东月考)如图,在四棱锥PABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3,E为PD的中点,点F在PC上,且=.求证:平面AEF⊥平面PCD.
6.3.2 空间线面关系的判定(1)
1. D 由直线l∥平面α,得m⊥n,则m·n=-a+2-6=0,所以a=-4.
2. C 因为平面α的一个法向量为(1,-2,-1),平面β的一个法向量为(-1,2,k),且α∥β,所以==,解得k=1.
3. C 若直线的方向向量a,b共线,则两直线平行或重合.又直线m,n是空间中两条不同的直线,所以两直线m,n平行,即“a,b共线”是“直线m,n平行”的充分条件;若直线m,n平行,则a,b共线,即“a,b共线”是“直线m,n平行”的必要条件.综上,“a,b共线”是“直线m,n平行”的充要条件.
4. B 建立如图所示的空间直角坐标系,设DA=a,DC=b,DD1=c,则A(a,0,0),C(0,b,0),D1(0,0,c),E(a,b,),B1(a,b,c),所以=(-a,b,0),=(-a,0,c),=(-a,-b,0).因为=λ,所以=(-λa,-λb,0),所以F((1-λ)a,(1-λ)b,c),所以=(-λa,-λb,).设平面ACD1的法向量为n=(x,y,z),则取x=bc,则y=ac,z=ab,所以n=(bc,ac,ab).因为EF∥平面ACD1,所以⊥n,所以·n=-λabc-λabc+=0,解得λ=.
5. B 因为e1,e2,e3为空间内三个不共面的向量,所以e1,e2,e3可以作为空间内的一个基底.又平面α和平面β的法向量分别为a=e1+λe2+3e3和b=-e1+2e2+μe3,且α∥β,所以a∥b,则a=tb,即e1+λe2+3e3=t(-e1+2e2+μe3),所以解得所以λ+μ=-5.
6. C 分别以,,的方向为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,则E(2,3,3),F(4,,0),G(4,3,),D1(0,3,3),B1(4,0,3),M(x,y,0),=(2,-,-3),=(0,,),=(x,y-3,-3).设平面EFG的法向量n=(x1,y1,z1),则得令y1=1,则n=(-,1,-1).由于直线D1M与平面EFG平行,故·n=0,则-x+y-3+3=0,即y=x.因为=(4-x,-y,3),=(-x,3-y,3),所以·=(4-x)·(-x)+(-y)·(3-y)+9=x2-4x+y2-3y+9=x2-4x+(x)2-+9=x2-x+9=(x-2)2+,由于x∈(0,4),故当x=2时,·取得最小值,最小值为.
7. AC 因为平面α与平面β平行,所以平面α的法向量与平面β的法向量平行.对于A,若(1,-2,3)=λ(-1,2,-3),则此时λ=-1,满足平面α的法向量与平面β的法向量平行,故A正确;对于B,若(-1,-2,3)=λ(-1,2,-3),则此时无解,不满足平面α的法向量与平面β的法向量平行,故B错误;对于C,若(2,-4,6)=λ(-1,2,-3),则此时λ=-2,满足平面α的法向量与平面β的法向量平行,故C正确;对于D,若(2,-4,-6)=λ(-1,2,-3),则此时无解,不满足平面α的法向量与平面β的法向量平行,故D错误.故选AC.
8. ABD 如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.设CC1,BC,CD,C1D1的中点分别为M,N,P,Q.不妨设棱长为2,则A1(2,0,2),B(2,2,0),C1(0,2,2),E(2,0,1),M(0,2,1),N(1,2,0),P(0,1,0),Q(0,1,2),=(0,2,-2),=(-2,2,0).设平面A1BC1的法向量为n=(x,y,z),则令y=1,则n=(1,1,1).又=(-2,2,0),=(-1,2,-1),=(-2,1,-1),=(-2,1,1),则·n=-2×1+2×1=0,·n=-1×1+2×1-1×1=0,·n=-2×1+1×1-1×1=-2,·n=-2×1+1×1+1×1=0,又EM,EN,EQ均不在平面A1BC1内,所以EM,EN,EQ都平行于平面A1BC1,即若直线EF∥平面A1BC1,则点F的位置可能是线段CC1的中点,线段BC的中点或线段C1D1的中点.故选ABD.
9. 平行 因为平面α的一个法向量为n1=(2,-3,1),=(1,0,-2),=(1,1,1),且n1·=(2,-3,1)·(1,0,-2)=2+0-2=0,所以n1⊥.同理可证n1⊥.又AB∩AC=A,AB 平面ABC,AC 平面ABC,所以n1⊥平面ABC.又n1为平面α的一个法向量,所以平面α∥平面ABC.
10. 1 -4 因为α∥β,所以u1∥u2,所以存在实数λ使得u1=λu2,即(-3,y,2)=λ(6,-2,z),所以解得
11. 以A为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系.由题意,得P(0,0,2),B(2,0,0),D(0,2,0),C(2,2,0),O(1,1,0),F(1,0,1),E(0,1,1),所以=(1,2,-1),=(-1,1,0).设平面EFC的法向量为n=(x,y,z),所以则取x=1,则y=1,z=3,所以n=(1,1,3).因为OG∥平面EFC,所以n·=0.设G(0,0,a),则=(-1,-1,a),所以-1-1+3a=0,解得a=,所以G(0,0,),即AG=.
12. 因为PA⊥底面ABCD,AB 平面ABCD,AD 平面ABCD,所以PA⊥AB,PA⊥AD.
由题意,得AB,AD,AP两两垂直,建立如图所示的空间直角坐标系Oxyz,
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,4,0),P(0,0,2),E(0,2,1),
所以=(2,2,0),=(0,2,1),=(-2,0,2),=(2,2,-2),
则=λ=(2λ,2λ,-2λ),
所以=+=(2λ-2,2λ,2-2λ).
设平面ACE的法向量为m=(x,y,z),
则即
取x=1,所以m=(1,-1,2).
因为BF∥平面ACE,
所以·m=2λ-2-2λ+4-4λ=0,解得λ=.
13. (1) 以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系.
设正方体的棱长为2,则A(2,0,0),C(0,2,0),D(0,0,0),M(1,0,1),N(1,1,0),P(1,2,1).
由正方体的性质知,AD⊥平面CC1D1D,
所以=(2,0,0)为平面CC1D1D的一个法向量.
因为=(0,1,-1),所以·=0×2+1×0+(-1)×0=0,
所以⊥.
又MN 平面CC1D1D,
所以MN∥平面CC1D1D.
(2) 因为=(2,0,0)为平面CC1D1D的一个法向量,且=(0,2,0),=(0,1,-1),
所以
即=(2,0,0)也是平面MNP的一个法向量,
所以平面MNP∥平面CC1D1D.
6.3.2 空间线面关系的判定(2)
1. D 因为α⊥β,所以n1⊥n2,所以n1·n2=×(-3)+x×+2×(-2)=0,解得x=7.
2. A 因为=(5,1,-7),=(2,-3,1),所以·=0,所以⊥,且||≠||,所以△ABC的形状是直角三角形.
3. A 因为直线l垂直于平面α,所以直线l的一个方向向量(m,2,4)与平面α的一个法向量(2,4,8)平行,即==,解得m=1.
4. D 以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,设正方体棱长为1,设M(0,0,a),N(x,1,1-x),则A(1,0,0),D1(0,0,1),所以=(x,1,1-x-a),=(-1,0,1).若AD1⊥MN,则·=-x+1-x-a=0,即2x=1-a(0≤x≤1,0≤a≤1),方程有无数组解.
5. D 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.由正方体ABCDA1B1C1D1的棱长为1,可得A(1,0,0),B(1,1,0),D1(0,0,1).设P(a,b,1),M(0,1,t)(0≤t≤1),则=(a-1,b,1),=(-1,-1,1),=(0,-1,1-t).因为AP⊥平面MBD1,所以AP⊥BD1,AP⊥MD1,即解得所以=(t,1-t,1),所以=+=(0,-1,0)+(t,1-t,1)=(t,-t,1),所以||==.因为0≤t≤1,结合复合函数单调性,得||=在区间[0,1]上单调递增.故||=∈[1,].
6. C 因为四边形ABCD为正方形,且平面PABE⊥平面ABCD,所以PA,AB,AD两两垂直,且PA∥BE,建立如图所示的空间直角坐标系Axyz.因为PD=8,CE=6,所以P(0,0,4),C(4,4,0),E(4,0,2),D(0,4,0),B(4,0,0),则F(4λ,0,0),=(4,-4,2),=(4λ,-4,0),=(0,-4,2),=(-4,0,2).设平面DEF的法向量为m=(x,y,z),则即所以令x=1,则m=(1,λ,2λ-2).设平面PCE的法向量为n=(a,b,c),则即所以令a=1,则n=(1,1,2).因为平面DEF⊥平面PCE,所以m·n=1+λ+2(2λ-2)=5λ-3=0,解得λ=.
7. AD 若a∥m,则l⊥α,故A正确;若a·m=0,则l∥α或l在α内,故B错误;若m∥n,则α∥β,故C错误;若m·n=0,则α⊥β,故D正确.故选AD.
8. ABC 以A1 为坐标原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1),D(0,1,),P(0,2,0),则=(1,0,1),=(0,1,),=(-1,2,0),=(1,-1,-).设平面A1BD的法向量为n=(x,y,z),则取z=-2,则x=2,y=1,所以平面A1BD的一个法向量为n=(2,1,-2).设=λ=λ(-1,2,0)=(-λ,2λ,0),则=+=(1-λ,-1+2λ,-).假设DQ⊥平面A1BD,所以也是平面A1BD的一个法向量,所以n=(2,1,-2)与=(1-λ,-1+2λ,-)共线,则===成立,所以则关于λ的方程组无解,故不存在点Q,使得DQ⊥平面A1BD,故A,B,C错误,D正确.故选ABC.
9. (0,,) 设H(a,b,c),则=(a,b-2,c),=(1,2,4),=(-1,2,4).因为PH⊥平面OAB,OA 平面OAB,OB 平面OAB,所以PH⊥OA,PH⊥OB,则解得a=0,b=2-2c,所以H(0,2-2c,c).因为PH⊥平面OAB,H为垂足,所以O,A,B,H四点共面,则存在唯一实数对(x,y)使得=x+y,即(0,2-2c,c)=(x-y,2x+2y,4x+4y),所以解得x=y=,c=,所以H(0,,).
10. (0,] 因为在矩形ABCD中,AB=1,AD=a,PD⊥平面ABCD,所以以D为坐标原点,DA,DC,DP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设DP=b,AQ=x(0
12. 由直三棱柱ABC-FGE,得CE⊥平面ABC.因为AC⊥BC,AC=BC=4,
所以三棱柱ABC-FGE的体积V=AC×BC×CE=×4×4×CE=32,解得EC=4.
因为三棱柱ABC-FGE为直三棱柱,
所以AC⊥CE,BC⊥CE.
因为AC⊥BC,所以CA,CB,CE两两垂直,
以C为坐标原点,CA,CB,CE所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则O(0,2,0),D(0,4,1),E(0,0,4),B(0,4,0),A(4,0,0),C(0,0,0),
则=(0,-4,3).设=λ=(0,-4λ,3λ),则Q(0,4-4λ,1+3λ),
故=(0,2-4λ,1+3λ).
因为OQ⊥DE,所以·=0,
所以0-8+16λ+3+9λ=0,解得λ=,
即Q(0,,),
所以=(0,-,),=(0,,),
所以·=(4,0,0)·(0,-,)=0,
·=(0,,)·(0,-,)=-+=0,
所以BQ⊥CA,BQ⊥CQ.
又CA 平面ACQ,CQ 平面ACQ,CA∩CQ=C,
所以BQ⊥平面ACQ.
13. 如图,以D为坐标原点,DA,DC所在直线分别为x轴,y轴,过点D作AP的平行线为z轴,建立如图所示的空间直角坐标系,则D(0,0,0),A(2,0,0),C(0,2,0),P(2,0,2),E(1,0,1),B(3,2,0),
所以=(0,2,0),=(-2,2,-2).
因为=,所以=,
所以=+=(-2,2,-2)+(2,0,2)=(,,),即F(,,),
所以=(-,,),=(-1,0,1).
设平面AEF的法向量为n=(x,y,z),
则
取x=z=1,则y=-1,所以n=(1,-1,1).
设平面PCD的法向量为m=(a,b,c),
则
取a=1,则c=-1,所以m=(1,0,-1),
所以n·m=1×1+(-1)×0+1×(-1)=0,
所以n⊥m,
所以平面AEF⊥平面PCD.
