6.3.3 空间角的计算 练习(2课时,含详解)2024-2025学年高二数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 6.3.3 空间角的计算 练习(2课时,含详解)2024-2025学年高二数学苏教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 613.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-18 00:00:00 | ||
图片预览



文档简介
6.3.3 空间角的计算(1)
一、 单项选择题
1 (2024抚州期中)已知点O(0,0,0),A(1,0,1),B(-1,1,2),C(-1,0,-1),则异面直线OC与AB所成角的余弦值为( )
A. B. C. D.
2 (2024中山期中)如图,圆锥的轴截面ABC为等边三角形,D为弧AB的中点,E,F分别为母线BC,AC的中点,则异面直线BF和DE所成角的大小为( )
A. B. C. D.
3 (2024海南期中)在四棱锥SABCD中,底面ABCD是菱形,∠ABC=60°,SA⊥平面ABCD,SA=AB,E是BC的中点,F是棱SD上一点(不含端点),满足=λ.若异面直线AE与CF所成角的余弦值为,则实数λ的值为( )
A. 2 B. 3 C. 4 D. 5
4 (2024福州期末)在正方体ABCDA1B1C1D1中,点P满足=+,则直线AC与平面A1DP所成角的正弦值为( )
A. B. C. D.
5 (2024广西期末)在如图所示的空间直角坐标系Axyz中,P(x,y,z)是正三棱柱ABCA1B1C1的底面A1B1C1内一动点,A1A=AB=2,直线PA和底面ABC所成的角为,则点P的坐标满足( )
A. x2+y2= B. x2+y2=2
C. x2+y2=3 D. x2+y2=4
6 如图,D是正方体的一个“直角尖”OABC(OA,OB,OC两两垂直且相等)的棱OB的中点,P是BC的中点,Q是AD上的一个动点,连接PQ,则当AC与PQ所成的角最小时,AQ∶QD等于( )
A. B. C. D. 2
二、 多项选择题
7 (2024日照期末)如图,在棱长为2的正方体ABCDA1B1C1D1中,E,F分别为棱DD1,C1D1的中点,则下列说法中正确的是( )
A. BC1∥AE
B. 三棱锥C1BB1D的体积为
C. 直线AF与直线BE所成角的余弦值为
D. 直线BB1与平面BDC1所成角的正弦值为
8 如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°,则下列说法中正确的是( )
A. 直线AD与直线BC所成角的大小为90°
B. 直线AB与直线CD所成角的余弦值为
C. 直线AD与平面BCD所成角的大小为45°
D. 直线AD与平面BCD所成角的大小为60°
三、 填空题
9 在空间直角坐标系Oxyz中,若平面ABC的一个法向量为m=(0,2,1),直线AP的一个方向向量为n=(1,1,1),则直线AP与平面ABC所成角的正弦值为________.
10 (2023华南师大附中期末)如图,在直三棱柱ABCA1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为________.
11 (2024南昌期末)在棱长为2的正方体ABCDA1B1C1D1中,点Q在线段B1C上运动,则直线C1Q与平面A1C1D所成角的正弦值的取值范围为________.
四、 解答题
12 (2023广州期末)如图,在长方体ABCDA1B1C1D1中,BC=4,AB=BB1=2,E是BB1的中点.求:
(1) BD1与AE所成角的余弦值;
(2) BD1与平面ACE所成角的正弦值.
13 (2024运城期中)如图,四棱锥PABCD的底面是矩形,平面PCD⊥平面ABCD,M是棱PD上的动点,N是棱AB上的一点,且=,CD=PD=2AD=PC.
(1) 求证:MN⊥AC;
(2) 若直线MN与平面MBC所成角的正弦值是,求点M的位置.
6.3.3 空间角的计算(2)
一、 单项选择题
1 已知△ABC为等边三角形,PA⊥平面ABC,且PA=AC,则二面角PBCA的大小为( )
A. 30° B. 45° C. 60° D. 75°
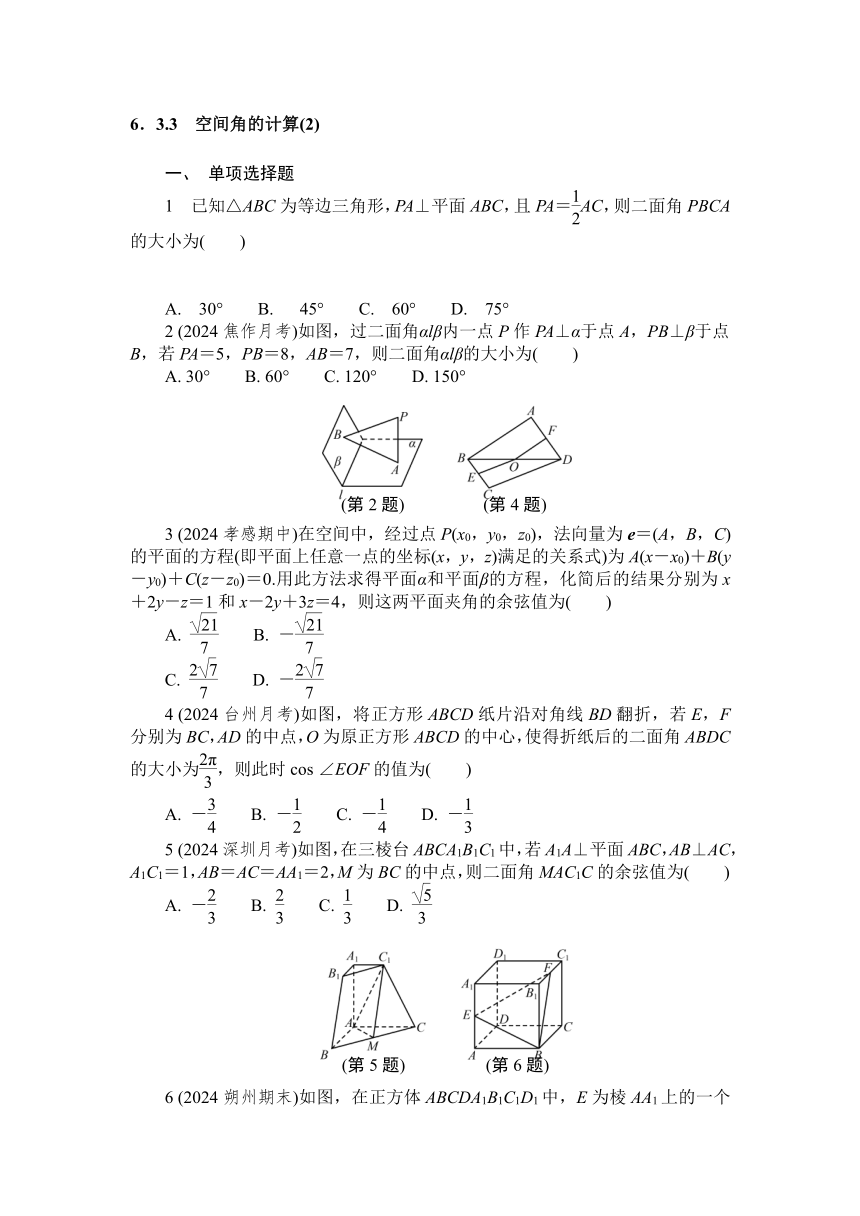
2 (2024焦作月考)如图,过二面角αlβ内一点P作PA⊥α于点A,PB⊥β于点B,若PA=5,PB=8,AB=7,则二面角αlβ的大小为( )
A. 30° B. 60° C. 120° D. 150°
3 (2024孝感期中)在空间中,经过点P(x0,y0,z0),法向量为e=(A,B,C)的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系式)为A(x-x0)+B(y-y0)+C(z-z0)=0.用此方法求得平面α和平面β的方程,化简后的结果分别为x+2y-z=1和x-2y+3z=4,则这两平面夹角的余弦值为( )
A. B. -
C. D. -
4 (2024台州月考)如图,将正方形ABCD纸片沿对角线BD翻折,若E,F分别为BC,AD的中点,O为原正方形ABCD的中心,使得折纸后的二面角ABDC的大小为,则此时cos ∠EOF的值为( )
A. - B. - C. - D. -
5 (2024深圳月考)如图,在三棱台ABCA1B1C1中,若A1A⊥平面ABC,AB⊥AC,A1C1=1,AB=AC=AA1=2,M为BC的中点,则二面角MAC1C的余弦值为( )
A. - B. C. D.
6 (2024朔州期末)如图,在正方体ABCDA1B1C1D1中,E为棱AA1上的一个动点,F为棱B1C1上的一个动点,则平面EFB与底面ABCD所成角的余弦值的取值范围是( )
A. [0,] B. [,]
C. [0,] D. [0,]
二、 多项选择题
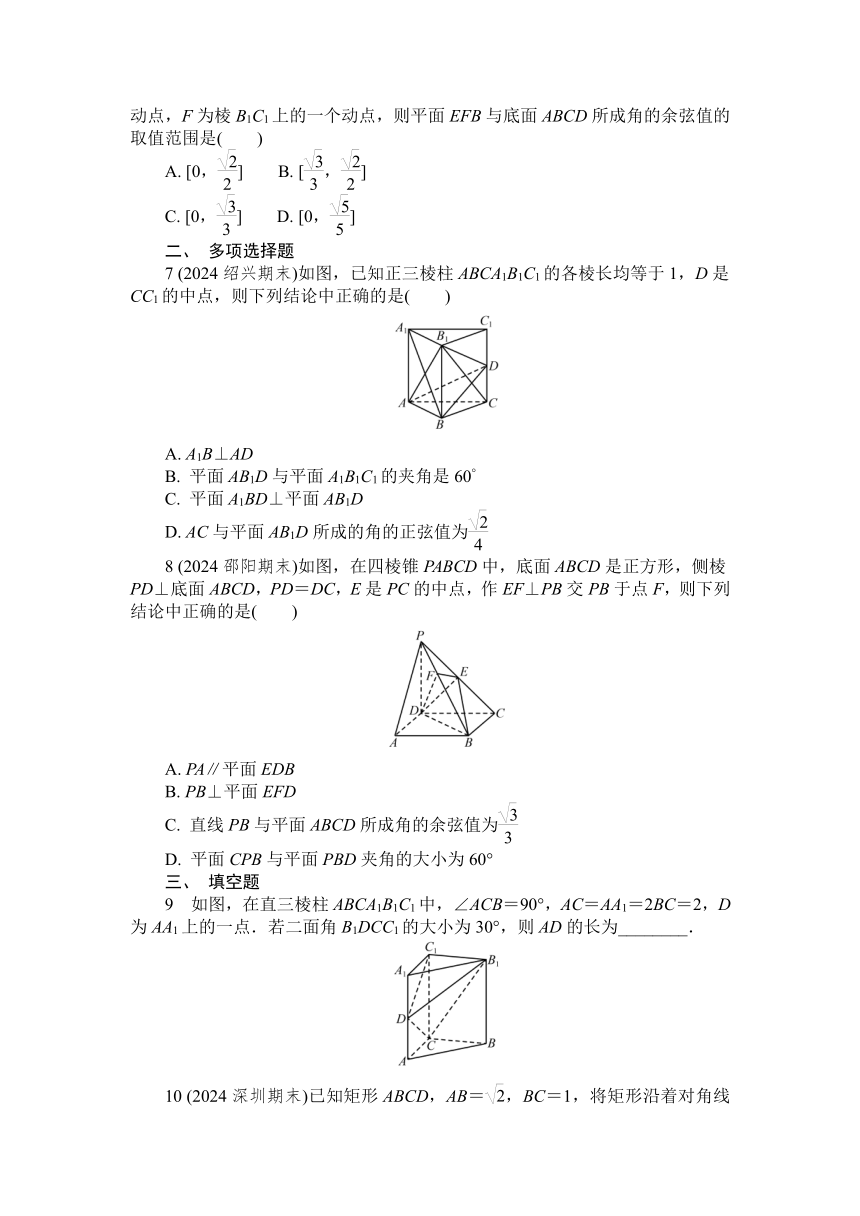
7 (2024绍兴期末)如图,已知正三棱柱ABCA1B1C1的各棱长均等于1,D是CC1的中点,则下列结论中正确的是( )
A. A1B⊥AD
B. 平面AB1D与平面A1B1C1的夹角是60°
C. 平面A1BD⊥平面AB1D
D. AC与平面AB1D所成的角的正弦值为
8 (2024邵阳期末)如图,在四棱锥PABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F,则下列结论中正确的是( )
A. PA∥平面EDB
B. PB⊥平面EFD
C. 直线PB与平面ABCD所成角的余弦值为
D. 平面CPB与平面PBD夹角的大小为60°
三、 填空题
9 如图,在直三棱柱ABCA1B1C1中,∠ACB=90°,AC=AA1=2BC=2,D为AA1上的一点.若二面角B1DCC1的大小为30°,则AD的长为________.
10 (2024深圳期末)已知矩形ABCD,AB=,BC=1,将矩形沿着对角线BD对折,形成一个空间四边形ABC′D,当AC′=时,二面角ABDC′的余弦值为________.
11 (2023深圳期末)如图,在Rt△ABC中,AB=1,BC=2,D为斜边AC上异于点A,C的动点,若将△ABD沿折痕BD翻折,使点A折至点A1处,且二面角A1BDC的大小为,则线段A1C长度的最小值为________.
四、 解答题
12 如图,在四棱锥PABCD中,PD⊥底面ABCD,底面ABCD是边长为2的菱形,∠DAB=60°,E是AD的中点.
(1) 求证:平面PBE⊥平面PAD;
(2) 直线PB与平面PAD所成的角为45°,求二面角CPED的余弦值.
13 如图,在正方体ABCDA1B1C1D1中,直线A1C与平面AB1D1和平面C1BD分别交于点G,H.
(1) 求证:G,H是线段A1C的三等分点;
(2) 在棱D1C1上是否存在点M,使得二面角MBDC1的大小为60°?若存在,求出的值;若不存在,请说明理由.
6.3.3 空间角的计算(1)
1. A 由题意,得=(-1,0,-1),=(-2,1,1).设异面直线OC与AB所成的角为θ,则cos θ=|cos 〈,〉|===.
2. C 取AB的中点O,连接OC,OD,以O为坐标原点,OD,OB,OC所在直线分别为x轴,y轴,z轴建立如图所示的空的间直角坐标系,设AB=2,则B(0,1,0),D(1,0,0),C(0,0,),A(0,-1,0).又E,F分别为BC,AC的中点,所以E(0,,),F(0,-,),则=(0,-,),=(-1,,).设异面直线BF和DE所成角为θ,则cos θ=|cos 〈,〉|===0.又θ∈(0,],所以θ=.
3. C 取CD的中点M,连接AM,AC.因为四边形ABCD是菱形,∠ABC=60°,所以△ABC,△ADC均为等边三角形.又因为M为CD的中点,所以AM⊥CD.又因为AB∥CD,所以AM⊥AB,以A为坐标原点,AB,AM,AS所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.设AB=SA=1,则A(0,0,0),S(0,0,1),E(,,0),C(,,0),D(-,,0).设m=,所以m(-,,-1)=(--xF,-yF,-zF),所以F((m-1),(1-m),m),所以=(-1,-m,m),=(,,0),所以|cos 〈,〉|===,化简,得16m2-8m+1=0,所以m=,所以=,所以=4,所以λ=4.
4. B 不妨设正方体ABCD-A1B1C1D1的棱长为3,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(3,0,0),C(3,3,0),D(0,3,0),A1(0,0,3),B1(3,0,3),所以=(0,3,0),=(0,0,3).设P(x,y,z),则=(x-3,y,z),+=(0,1,2).因为=+,所以(x-3,y,z)=(0,1,2),即解得所以P(3,1,2),=(3,-2,2),=(3,3,0),=(0,-3,3).设平面A1DP的法向量为n=(x1,y1,z1),则即令z1=1,则x1=0,y1=1,所以n=(0,1,1).设直线AC与平面A1DP所成角为θ,则sin θ=|cos 〈,n〉|===,所以直线AC与平面A1DP所成角的正弦值为.
5. A 由题意,得A(0,0,0),A1(0,0,2).因为P(x,y,z)是正三棱柱ABC-A1B1C1的底面A1B1C1内一动点,则z=2,所以=(-x,-y,-z).又AA1⊥平面ABC,所以=(0,0,2)是平面ABC的一个法向量.因为直线PA和底面ABC所成的角为,所以|cos 〈,〉|====,整理,得z2=3x2+3y2.又z=2,所以x2+y2=.
6. C 由题意,得OA,OB,OC两两垂直,故以O为坐标原点,建立如图所示的空间直角坐标系.设OA=OB=OC=2,则O(0,0,0),A(0,0,2),C(0,2,0),P(1,1,0),D(1,0,0),则=m+(1-m)=m(0,0,2)+(1-m)(1,0,0)=(1-m,0,2m),m∈[0,1],则Q(1-m,0,2m).又=(0,2,-2),=(-m,-1,2m).设直线AC,PQ所成角为θ,θ∈[0,],则cos θ=|cos 〈,〉|==×.令y==,2m+1=t,t∈[1,3],则y==.令=n,n∈,则y=≤,此时n=,t=,m=,故当m=时,cos θ取得最大值,此时θ最小,点Q(,0,),则=(,0,-),=(,0,-),故=,则AQ∶QD=.
7. BC 在棱长为2的正方体ABCD-A1B1C1D1中,建立如图所示的空间直角坐标系,则D(0,0,0),A(2,0,0),B(2,2,0),B1(2,2,2),C1(0,2,2),E(0,0,1),F(0,1,2).对于A,=(-2,0,2),=(-2,0,1),显然与不共线,所以BC1与AE不平行,故A错误;对于B,三棱锥C1-BB1D的体积VC1-BB1D=VD-BB1C1=S△BB1C1·DC=××2×2×2=,故B正确;对于C,=(-2,1,2),=(-2,-2,1),cos 〈,〉===,所以直线AF与直线BE所成角的余弦值为,故C正确;对于D,=(2,2,0),=(0,2,2),设平面BDC1的法向量n=(x,y,z),则令x=1,得n=(1,-1,1).令直线BB1与平面BDC1所成的角为θ.又=(0,0,2),所以sin θ=|cos 〈n,〉|===,故D错误.故选BC.
8. ABC 以B为坐标原点,建立如图所示的空间直角坐标系B-xyz.设AB=2,则A(0,-1,),C(0,2,0),D(,-1,0),所以=(,0,-),=(0,2,0),=(0,1,-),=(,-3,0).因为·=0,所以AD⊥BC,即直线AD与直线BC所成角的大小为90°,故A正确;因为|cos 〈,〉|==,所以直线AB与直线CD所成角的余弦值为,故B正确;设AD与平面BCD所成角为θ,因为n=(0,0,1)是平面BCD的一个法向量,所以sin θ=|cos 〈,n〉|==,所以θ=45°,即直线AD与平面BCD所成角的大小为45°,故C正确,D错误.故选ABC.
9. 设直线AP与平面ABC所成角为α.因为平面ABC的一个法向量m=(0,2,1),直线AP的一个方向向量为n=(1,1,1),所以sin α===.
10. 由题意,得CC1,CB,CA两两垂直,故以{,,}为正交基底建立空间直角坐标系C xyz.不妨设BC=CA=CC1=2.因为M,N分别是A1B1,A1C1的中点,所以N(1,0,2),A(2,0,0),B(0,2,0),M(1,1,2),则=(-1,0,2),=(1,-1,2).设直线BM与AN所成角为α,则cos α=|cos 〈,〉|===,所以BM与AN所成角的余弦值为.
11. [,] 以{,,}为正交基底,建立如图所示的空间直角坐标系,则A1(2,0,2),C1(0,2,2),D(0,0,0).设Q(a,2,a),0≤a≤2,则=(2,0,2),=(0,2,2),=(a,0,a-2).设平面A1C1D的法向量为n=(x,y,z),则取x=1,得n=(1,1,-1).设直线C1Q与平面A1C1D所成角为θ,则sin θ===,当0≤a≤2时,2≤2(a-1)2+2≤4,则≤sin θ≤.
12. (1) 以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(2,4,0),D(0,4,0),A1(0,0,2),B1(2,0,2),C1(2,4,2),D1(0,4,2),E(2,0,1),
所以=(-2,4,2),=(2,0,1),
则cos 〈,〉===-,则BD1与AE所成角的余弦值为.
(2) 设平面ACE的法向量为n=(x,y,z).
因为=(2,4,0),=(2,0,1),=(-2,4,2),
所以即
令y=1,则n=(-2,1,4),
所以cos 〈,n〉===,
故BD1与平面ACE所成角的正弦值为.
13. (1) 因为CD=PD=PC,
所以CD2+PD2=PC2,所以PD⊥CD.
因为平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,PD 平面PCD,
所以PD⊥平面ABCD.
因为AD 平面ABCD,
所以PD⊥AD.
因为四边形ABCD是矩形,所以AD⊥CD,
故DA,DC,DP两两垂直.
以D为坐标原点,DA,DC,DP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设CD=4,则A(2,0,0),C(0,4,0),B(2,4,0),N(2,1,0),M(0,0,t)(0≤t≤4),
所以=(2,1,-t),=(-2,4,0).
因为·=2×(-2)+1×4+(-t)×0=0,
所以⊥,即MN⊥AC.
(2) 由(1),得=(2,1,-t),=(2,0,0),=(0,-4,t).
设m=(x,y,z)为平面MBC的法向量,
则
令y=t,得x=0,z=4,所以m=(0,t,4).
设直线MN与平面MBC所成角为θ,
则sin θ=|cos 〈m,〉|==,
所以(t2-20)(t2-4)=0,
因为0≤t≤4,所以t=2,即M是棱PD的中点.
6.3.3 空间角的计算(2)
1. A 如图,取BC的中点D,连接AD,PD.由题意,得PD⊥BC,AD⊥BC,所以∠PDA为二面角PBCA的平面角.以A为坐标原点,AD所在的直线为y轴,AP所在的直线为z轴,建立如图所示的空间直角坐标系A-xyz,设PA=1,则A(0,0,0),D(0,,0),P(0,0,1),则=(0,-,0),=(0,-,1),所以cos 〈,〉===,所以〈,〉的大小为30°,所以∠PDA=30°,即二面角P-BC-A 的大小为30°.
2. C 设=a,=b,则=b-a,且|a|=5,|b|=8,||=7.因为||2=|b-a|2=b2+a2-2a·b,解得a·b=20,所以cos 〈a,b〉===.又0°≤〈a,b〉≤180°,所以∠APB=〈a,b〉=60°,所以二面角α-l-β的大小为120°.
3. A 由题意,得平面α和平面β的法向量分别为n1=(1,2,-1),n2=(1,-2,3),故两平面夹角的余弦值为|cos 〈n1,n2〉|===.
4. A 如图,易知OA⊥BD,OC⊥BD,所以⊥,⊥,〈,〉=π,〈,〉=,易知=(+),=(+).设正方形的边长为2,所以OA=OB=OC=OD=,OE=OF=1,cos 〈,〉==×(·+·+·+·)=-.
5. B 根据棱台的性质可知A1B1=1,由于A1A⊥平面ABC,AB 平面ABC,AC 平面ABC,故A1A⊥AB,A1A⊥AC.又AB⊥AC,所以AB,AC,AA1两两垂直,故以A为坐标原点,AB,AC,AA1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,平面CC1A的一个法向量为m=(1,0,0),M(1,1,0),C1(0,1,2),即=(1,1,0),=(0,1,2).设平面MAC1的法向量为n=(x,y,z),则故可得平面MAC1的一个法向量为n=(2,-2,1).设二面角M-AC1-C的平面角为θ,由图可知θ为锐角,所以cos θ==.
6. A 设平面EFB与底面ABCD所成的二面角的平面角为θ,由图可得θ不为钝角.以D为坐标原点,建立如图所示的空间直角坐标系,设正方体的棱长为1,则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),E(1,0,m),F(n,1,1),所以=(0,-1,m),=(n-1,0,1).设平面EFB的法向量为n=(x,y,z),则即令x=-1,则y=m(n-1),z=n-1,故n=(-1,m(n-1),n-1).又底面ABCD的一个法向量为m=(0,0,1),所以cos θ=|cos 〈n,m〉|==.因为m,n∈[0,1],所以cos θ=,当n=1时,cos θ=0;当n≠1时,cos θ=,n∈[0,1),m∈[0,1],则(1-n)2∈(0,1],m2∈[0,1],则∈[1,+∞),则当n=0,m=0时,分母取到最小值,此时(cos θ)max=;当n→1,n>0时,则→0,此时cos θ∈(0,].综上,cos θ∈[0,].
7. ACD 取线段AB的中点O,连接CO.在正三棱柱ABC-A1B1C1中,AA1⊥平面ABC.因为△ABC是边长为1的等边三角形,所以CO⊥AB,以O为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,则A(-,0,0),B(,0,0),C(0,,0),A1(-,0,1),B1(,0,1),C1(0,,1),D(0,,).对于A,=(1,0,-1),=(,,),所以·=+0-=0,则A1B⊥AD,故A正确;对于B,设平面AB1D的法向量为m=(x1,y1,z1),=(1,0,1),=(,,),则令x1=1,则z1=-1,y1=0,可得m=(1,0,-1),易知平面A1B1C1的一个法向量为u=(0,0,1),所以cos 〈m,u〉==-=-,所以平面AB1D与平面A1B1C1的夹角为45°,故B错误;对于C,设平面A1BD的法向量为n=(x2,y2,z2),=(1,0,-1),=(,,-),则取x2=1,则z2=1,y2=0,可得n=(1,0,1),则m·n=1+0-1=0,所以m⊥n,故平面A1BD⊥平面AB1D,故C正确;对于D,=(,,0),则cos 〈,m〉===,所以AC与平面AB1D所成的角的正弦值为,故D正确.故选ACD.
8. ABD 以D为坐标原点,DA,DC,DP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设DC=1.对于A,由题意,得A(1,0,0),B(1,1,0),P(0,0,1),E(0,,),所以=(1,0,-1),=(1,1,0),=(0,,).设平面EDB的法向量为m=(x1,y1,z1),则取x1=1,则y1=-1,z1=1,所以m=(1,-1,1),则·m=0.因为PA 平面EDB,所以PA∥平面EDB,故A正确;对于B,=(1,1,-1),因为·=0+-=0,所以PB⊥ED.又EF⊥PB,且EF∩DE=E,EF 平面EFD,DE 平面EFD,所以PB⊥平面EFD,故B正确;对于C,因为侧棱PD⊥底面ABCD,所以∠PBD为直线PB与平面ABCD所成的角.又因为BD==,PB==,所以cos ∠PBD===,故C错误;对于D,由题意,得C(0,1,0),且=(1,0,0),=(0,1,-1).设平面CPB的法向量为n=(x2,y2,z2),则取y2=1,则z2=1,x2=0,所以n=(0,1,1).因为PD⊥底面ABCD,AC 平面ABCD,所以PD⊥AC.因为四边形ABCD是正方形,所以DB⊥AC.又DB∩PD=D,DB 平面PBD,PD 平面PBD,所以AC⊥平面PBD,则平面PBD的一个法向量为=(1,-1,0),所以cos 〈n,〉==-,所以平面CPB与平面PBD的夹角为60°,故D正确.故选ABD.
9. 以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系C-xyz,则C(0,0,0),B1(0,1,2),B(0,1,0),所以1=(0,1,2),=(0,1,0).设AD=a(0≤a≤2),则点D的坐标为(2,0,a),=(2,0,a).设平面B1CD的法向量为m=(x,y,z),则即令z=-1,得m=(,2,-1).又平面C1DC的一个法向量为=(0,1,0),记为n,则由cos 30°===,解得a=(负值舍去),故AD=.
10. 在△ABD和△BC′D中,分别过点A,C′作AM⊥BD,C′N⊥BD,垂足分别为M,N.由S△ABD=AM·BD=AB·AD,代入BD==,AB=,AD=1,得AM==,所以DM===,同理,C′N=,BN=,所以MN=.设二面角A-BD-C′大小为θ(0≤θ≤π),则与夹角为π-θ,由=++,得||2=||2+||2+||2+2·+2·+2·,所以=+++0+2×cos (π-θ)+0,解得cos θ=,所以二面角A-BD-C′的余弦值为.
11. 过点A1在平面A1BD内作A1M⊥BD,垂足为M,过点C在平面BCD内作CN⊥直线BD,垂足为N,如图所示.因为=++,·=·=0,记∠A1BD=α,则α∈(0,),∠NBC=-α,则||=sin α,||=2sin (-α)=2cos α.因为二面角A1-BD-C的大小为,所以,的夹角为.因为·=-·=-||·||cos =-sin αcos α,且||=|||-|||=|2cos (-α)-cos α|=|2sin α-cos α|,所以||2=(++)2=||2+||2+||2+2·=sin 2α+(2sin α-cos α)2+4cos 2α-2sin αcos α=5-3sin 2α≥2,即||≥,当且仅当sin 2α=1,即α=时,等号成立,故线段A1C长度的最小值为.
12. (1) 连接BD.因为AB=AD,∠DAB=60°,所以△ABD是等边三角形.
又E是AD的中点,所以BE⊥AD.
因为PD⊥平面ABCD,BE 平面ABCD,
所以PD⊥BE,又PD∩AD=D,PD 平面PAD,AD 平面PAD,
所以BE⊥平面PAD,又BE 平面PBE,
所以平面PBE⊥平面PAD.
(2) 因为BE⊥平面PAD,所以∠BPE为PB与平面PAD所成的角,即∠BPE=45°.
又PE 平面PAD,所以BE⊥PE.
因为△ABD是边长为2的等边三角形,所以PE=BE=,所以PD==.
以E为坐标原点,建立如图所示的空间直角坐标系,则P(-1,0,),E(0,0,0),C(-2,,0),
所以=(-1,0,),=(-2,,0).
设平面PEC的法向量为m=(x,y,z),
则即
令x=1,得m=(1,,).
因为BE⊥平面PAD,所以n=(0,1,0)为平面PED的一个法向量,
所以cos 〈m,n〉===,
显然二面角C-PE-D为锐角,
所以二面角C-PE-D的余弦值为.
13. (1) 连接A1B,交AB1 于点O.
在正方体ABCD-A1B1C1D1 中,A1B⊥AB1,且BC⊥平面A1B1BA.
因为AB1 平面A1B1BA,
所以BC⊥AB1.
又A1B∩BC=B,A1B 平面A1BC,BC 平面A1BC,
所以AB1⊥平面A1BC.
因为A1C 平面A1BC,
所以AB1⊥A1C,同理B1D1⊥A1C.
又AB1∩B1D1=B1,AB1 平面AB1D1,B1D1 平面AB1D1,
所以A1C⊥平面AB1D1.
设正方体的棱长为1,
则由VA-A1B1D1=VA1-AB1D1,
得××1×1×1=××()2·A1G,
解得A1G=,
同理HC=.
由题意,得A1C=,
所以G,H是线段A1C的三等分点.
(2) 以D为坐标原点,DA,DC,DD1 所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
假设存在点M满足题意,设正方体的棱长为1,则令=m,m∈[0,1],则M(0,m,1),B(1,1,0),A1(1,0,1),C(0,1,0).
由(1)知是平面C1BD的一个法向量,且=(-1,1,-1),=(0,m,1),=(1,1,0).
设平面MBD的法向量为n=(x,y,z),
则即
取y=1,则n=(-1,1,-m).
由cos 60°=,得=,
解得m=-8±3 [0,1],
故棱D1C1 上不存在点M,使得二面角M-BD-C1 的大小为60°.
一、 单项选择题
1 (2024抚州期中)已知点O(0,0,0),A(1,0,1),B(-1,1,2),C(-1,0,-1),则异面直线OC与AB所成角的余弦值为( )
A. B. C. D.
2 (2024中山期中)如图,圆锥的轴截面ABC为等边三角形,D为弧AB的中点,E,F分别为母线BC,AC的中点,则异面直线BF和DE所成角的大小为( )
A. B. C. D.
3 (2024海南期中)在四棱锥SABCD中,底面ABCD是菱形,∠ABC=60°,SA⊥平面ABCD,SA=AB,E是BC的中点,F是棱SD上一点(不含端点),满足=λ.若异面直线AE与CF所成角的余弦值为,则实数λ的值为( )
A. 2 B. 3 C. 4 D. 5
4 (2024福州期末)在正方体ABCDA1B1C1D1中,点P满足=+,则直线AC与平面A1DP所成角的正弦值为( )
A. B. C. D.
5 (2024广西期末)在如图所示的空间直角坐标系Axyz中,P(x,y,z)是正三棱柱ABCA1B1C1的底面A1B1C1内一动点,A1A=AB=2,直线PA和底面ABC所成的角为,则点P的坐标满足( )
A. x2+y2= B. x2+y2=2
C. x2+y2=3 D. x2+y2=4
6 如图,D是正方体的一个“直角尖”OABC(OA,OB,OC两两垂直且相等)的棱OB的中点,P是BC的中点,Q是AD上的一个动点,连接PQ,则当AC与PQ所成的角最小时,AQ∶QD等于( )
A. B. C. D. 2
二、 多项选择题
7 (2024日照期末)如图,在棱长为2的正方体ABCDA1B1C1D1中,E,F分别为棱DD1,C1D1的中点,则下列说法中正确的是( )
A. BC1∥AE
B. 三棱锥C1BB1D的体积为
C. 直线AF与直线BE所成角的余弦值为
D. 直线BB1与平面BDC1所成角的正弦值为
8 如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°,则下列说法中正确的是( )
A. 直线AD与直线BC所成角的大小为90°
B. 直线AB与直线CD所成角的余弦值为
C. 直线AD与平面BCD所成角的大小为45°
D. 直线AD与平面BCD所成角的大小为60°
三、 填空题
9 在空间直角坐标系Oxyz中,若平面ABC的一个法向量为m=(0,2,1),直线AP的一个方向向量为n=(1,1,1),则直线AP与平面ABC所成角的正弦值为________.
10 (2023华南师大附中期末)如图,在直三棱柱ABCA1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为________.
11 (2024南昌期末)在棱长为2的正方体ABCDA1B1C1D1中,点Q在线段B1C上运动,则直线C1Q与平面A1C1D所成角的正弦值的取值范围为________.
四、 解答题
12 (2023广州期末)如图,在长方体ABCDA1B1C1D1中,BC=4,AB=BB1=2,E是BB1的中点.求:
(1) BD1与AE所成角的余弦值;
(2) BD1与平面ACE所成角的正弦值.
13 (2024运城期中)如图,四棱锥PABCD的底面是矩形,平面PCD⊥平面ABCD,M是棱PD上的动点,N是棱AB上的一点,且=,CD=PD=2AD=PC.
(1) 求证:MN⊥AC;
(2) 若直线MN与平面MBC所成角的正弦值是,求点M的位置.
6.3.3 空间角的计算(2)
一、 单项选择题
1 已知△ABC为等边三角形,PA⊥平面ABC,且PA=AC,则二面角PBCA的大小为( )
A. 30° B. 45° C. 60° D. 75°
2 (2024焦作月考)如图,过二面角αlβ内一点P作PA⊥α于点A,PB⊥β于点B,若PA=5,PB=8,AB=7,则二面角αlβ的大小为( )
A. 30° B. 60° C. 120° D. 150°
3 (2024孝感期中)在空间中,经过点P(x0,y0,z0),法向量为e=(A,B,C)的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系式)为A(x-x0)+B(y-y0)+C(z-z0)=0.用此方法求得平面α和平面β的方程,化简后的结果分别为x+2y-z=1和x-2y+3z=4,则这两平面夹角的余弦值为( )
A. B. -
C. D. -
4 (2024台州月考)如图,将正方形ABCD纸片沿对角线BD翻折,若E,F分别为BC,AD的中点,O为原正方形ABCD的中心,使得折纸后的二面角ABDC的大小为,则此时cos ∠EOF的值为( )
A. - B. - C. - D. -
5 (2024深圳月考)如图,在三棱台ABCA1B1C1中,若A1A⊥平面ABC,AB⊥AC,A1C1=1,AB=AC=AA1=2,M为BC的中点,则二面角MAC1C的余弦值为( )
A. - B. C. D.
6 (2024朔州期末)如图,在正方体ABCDA1B1C1D1中,E为棱AA1上的一个动点,F为棱B1C1上的一个动点,则平面EFB与底面ABCD所成角的余弦值的取值范围是( )
A. [0,] B. [,]
C. [0,] D. [0,]
二、 多项选择题
7 (2024绍兴期末)如图,已知正三棱柱ABCA1B1C1的各棱长均等于1,D是CC1的中点,则下列结论中正确的是( )
A. A1B⊥AD
B. 平面AB1D与平面A1B1C1的夹角是60°
C. 平面A1BD⊥平面AB1D
D. AC与平面AB1D所成的角的正弦值为
8 (2024邵阳期末)如图,在四棱锥PABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F,则下列结论中正确的是( )
A. PA∥平面EDB
B. PB⊥平面EFD
C. 直线PB与平面ABCD所成角的余弦值为
D. 平面CPB与平面PBD夹角的大小为60°
三、 填空题
9 如图,在直三棱柱ABCA1B1C1中,∠ACB=90°,AC=AA1=2BC=2,D为AA1上的一点.若二面角B1DCC1的大小为30°,则AD的长为________.
10 (2024深圳期末)已知矩形ABCD,AB=,BC=1,将矩形沿着对角线BD对折,形成一个空间四边形ABC′D,当AC′=时,二面角ABDC′的余弦值为________.
11 (2023深圳期末)如图,在Rt△ABC中,AB=1,BC=2,D为斜边AC上异于点A,C的动点,若将△ABD沿折痕BD翻折,使点A折至点A1处,且二面角A1BDC的大小为,则线段A1C长度的最小值为________.
四、 解答题
12 如图,在四棱锥PABCD中,PD⊥底面ABCD,底面ABCD是边长为2的菱形,∠DAB=60°,E是AD的中点.
(1) 求证:平面PBE⊥平面PAD;
(2) 直线PB与平面PAD所成的角为45°,求二面角CPED的余弦值.
13 如图,在正方体ABCDA1B1C1D1中,直线A1C与平面AB1D1和平面C1BD分别交于点G,H.
(1) 求证:G,H是线段A1C的三等分点;
(2) 在棱D1C1上是否存在点M,使得二面角MBDC1的大小为60°?若存在,求出的值;若不存在,请说明理由.
6.3.3 空间角的计算(1)
1. A 由题意,得=(-1,0,-1),=(-2,1,1).设异面直线OC与AB所成的角为θ,则cos θ=|cos 〈,〉|===.
2. C 取AB的中点O,连接OC,OD,以O为坐标原点,OD,OB,OC所在直线分别为x轴,y轴,z轴建立如图所示的空的间直角坐标系,设AB=2,则B(0,1,0),D(1,0,0),C(0,0,),A(0,-1,0).又E,F分别为BC,AC的中点,所以E(0,,),F(0,-,),则=(0,-,),=(-1,,).设异面直线BF和DE所成角为θ,则cos θ=|cos 〈,〉|===0.又θ∈(0,],所以θ=.
3. C 取CD的中点M,连接AM,AC.因为四边形ABCD是菱形,∠ABC=60°,所以△ABC,△ADC均为等边三角形.又因为M为CD的中点,所以AM⊥CD.又因为AB∥CD,所以AM⊥AB,以A为坐标原点,AB,AM,AS所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.设AB=SA=1,则A(0,0,0),S(0,0,1),E(,,0),C(,,0),D(-,,0).设m=,所以m(-,,-1)=(--xF,-yF,-zF),所以F((m-1),(1-m),m),所以=(-1,-m,m),=(,,0),所以|cos 〈,〉|===,化简,得16m2-8m+1=0,所以m=,所以=,所以=4,所以λ=4.
4. B 不妨设正方体ABCD-A1B1C1D1的棱长为3,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(3,0,0),C(3,3,0),D(0,3,0),A1(0,0,3),B1(3,0,3),所以=(0,3,0),=(0,0,3).设P(x,y,z),则=(x-3,y,z),+=(0,1,2).因为=+,所以(x-3,y,z)=(0,1,2),即解得所以P(3,1,2),=(3,-2,2),=(3,3,0),=(0,-3,3).设平面A1DP的法向量为n=(x1,y1,z1),则即令z1=1,则x1=0,y1=1,所以n=(0,1,1).设直线AC与平面A1DP所成角为θ,则sin θ=|cos 〈,n〉|===,所以直线AC与平面A1DP所成角的正弦值为.
5. A 由题意,得A(0,0,0),A1(0,0,2).因为P(x,y,z)是正三棱柱ABC-A1B1C1的底面A1B1C1内一动点,则z=2,所以=(-x,-y,-z).又AA1⊥平面ABC,所以=(0,0,2)是平面ABC的一个法向量.因为直线PA和底面ABC所成的角为,所以|cos 〈,〉|====,整理,得z2=3x2+3y2.又z=2,所以x2+y2=.
6. C 由题意,得OA,OB,OC两两垂直,故以O为坐标原点,建立如图所示的空间直角坐标系.设OA=OB=OC=2,则O(0,0,0),A(0,0,2),C(0,2,0),P(1,1,0),D(1,0,0),则=m+(1-m)=m(0,0,2)+(1-m)(1,0,0)=(1-m,0,2m),m∈[0,1],则Q(1-m,0,2m).又=(0,2,-2),=(-m,-1,2m).设直线AC,PQ所成角为θ,θ∈[0,],则cos θ=|cos 〈,〉|==×.令y==,2m+1=t,t∈[1,3],则y==.令=n,n∈,则y=≤,此时n=,t=,m=,故当m=时,cos θ取得最大值,此时θ最小,点Q(,0,),则=(,0,-),=(,0,-),故=,则AQ∶QD=.
7. BC 在棱长为2的正方体ABCD-A1B1C1D1中,建立如图所示的空间直角坐标系,则D(0,0,0),A(2,0,0),B(2,2,0),B1(2,2,2),C1(0,2,2),E(0,0,1),F(0,1,2).对于A,=(-2,0,2),=(-2,0,1),显然与不共线,所以BC1与AE不平行,故A错误;对于B,三棱锥C1-BB1D的体积VC1-BB1D=VD-BB1C1=S△BB1C1·DC=××2×2×2=,故B正确;对于C,=(-2,1,2),=(-2,-2,1),cos 〈,〉===,所以直线AF与直线BE所成角的余弦值为,故C正确;对于D,=(2,2,0),=(0,2,2),设平面BDC1的法向量n=(x,y,z),则令x=1,得n=(1,-1,1).令直线BB1与平面BDC1所成的角为θ.又=(0,0,2),所以sin θ=|cos 〈n,〉|===,故D错误.故选BC.
8. ABC 以B为坐标原点,建立如图所示的空间直角坐标系B-xyz.设AB=2,则A(0,-1,),C(0,2,0),D(,-1,0),所以=(,0,-),=(0,2,0),=(0,1,-),=(,-3,0).因为·=0,所以AD⊥BC,即直线AD与直线BC所成角的大小为90°,故A正确;因为|cos 〈,〉|==,所以直线AB与直线CD所成角的余弦值为,故B正确;设AD与平面BCD所成角为θ,因为n=(0,0,1)是平面BCD的一个法向量,所以sin θ=|cos 〈,n〉|==,所以θ=45°,即直线AD与平面BCD所成角的大小为45°,故C正确,D错误.故选ABC.
9. 设直线AP与平面ABC所成角为α.因为平面ABC的一个法向量m=(0,2,1),直线AP的一个方向向量为n=(1,1,1),所以sin α===.
10. 由题意,得CC1,CB,CA两两垂直,故以{,,}为正交基底建立空间直角坐标系C xyz.不妨设BC=CA=CC1=2.因为M,N分别是A1B1,A1C1的中点,所以N(1,0,2),A(2,0,0),B(0,2,0),M(1,1,2),则=(-1,0,2),=(1,-1,2).设直线BM与AN所成角为α,则cos α=|cos 〈,〉|===,所以BM与AN所成角的余弦值为.
11. [,] 以{,,}为正交基底,建立如图所示的空间直角坐标系,则A1(2,0,2),C1(0,2,2),D(0,0,0).设Q(a,2,a),0≤a≤2,则=(2,0,2),=(0,2,2),=(a,0,a-2).设平面A1C1D的法向量为n=(x,y,z),则取x=1,得n=(1,1,-1).设直线C1Q与平面A1C1D所成角为θ,则sin θ===,当0≤a≤2时,2≤2(a-1)2+2≤4,则≤sin θ≤.
12. (1) 以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(2,4,0),D(0,4,0),A1(0,0,2),B1(2,0,2),C1(2,4,2),D1(0,4,2),E(2,0,1),
所以=(-2,4,2),=(2,0,1),
则cos 〈,〉===-,则BD1与AE所成角的余弦值为.
(2) 设平面ACE的法向量为n=(x,y,z).
因为=(2,4,0),=(2,0,1),=(-2,4,2),
所以即
令y=1,则n=(-2,1,4),
所以cos 〈,n〉===,
故BD1与平面ACE所成角的正弦值为.
13. (1) 因为CD=PD=PC,
所以CD2+PD2=PC2,所以PD⊥CD.
因为平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,PD 平面PCD,
所以PD⊥平面ABCD.
因为AD 平面ABCD,
所以PD⊥AD.
因为四边形ABCD是矩形,所以AD⊥CD,
故DA,DC,DP两两垂直.
以D为坐标原点,DA,DC,DP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设CD=4,则A(2,0,0),C(0,4,0),B(2,4,0),N(2,1,0),M(0,0,t)(0≤t≤4),
所以=(2,1,-t),=(-2,4,0).
因为·=2×(-2)+1×4+(-t)×0=0,
所以⊥,即MN⊥AC.
(2) 由(1),得=(2,1,-t),=(2,0,0),=(0,-4,t).
设m=(x,y,z)为平面MBC的法向量,
则
令y=t,得x=0,z=4,所以m=(0,t,4).
设直线MN与平面MBC所成角为θ,
则sin θ=|cos 〈m,〉|==,
所以(t2-20)(t2-4)=0,
因为0≤t≤4,所以t=2,即M是棱PD的中点.
6.3.3 空间角的计算(2)
1. A 如图,取BC的中点D,连接AD,PD.由题意,得PD⊥BC,AD⊥BC,所以∠PDA为二面角PBCA的平面角.以A为坐标原点,AD所在的直线为y轴,AP所在的直线为z轴,建立如图所示的空间直角坐标系A-xyz,设PA=1,则A(0,0,0),D(0,,0),P(0,0,1),则=(0,-,0),=(0,-,1),所以cos 〈,〉===,所以〈,〉的大小为30°,所以∠PDA=30°,即二面角P-BC-A 的大小为30°.
2. C 设=a,=b,则=b-a,且|a|=5,|b|=8,||=7.因为||2=|b-a|2=b2+a2-2a·b,解得a·b=20,所以cos 〈a,b〉===.又0°≤〈a,b〉≤180°,所以∠APB=〈a,b〉=60°,所以二面角α-l-β的大小为120°.
3. A 由题意,得平面α和平面β的法向量分别为n1=(1,2,-1),n2=(1,-2,3),故两平面夹角的余弦值为|cos 〈n1,n2〉|===.
4. A 如图,易知OA⊥BD,OC⊥BD,所以⊥,⊥,〈,〉=π,〈,〉=,易知=(+),=(+).设正方形的边长为2,所以OA=OB=OC=OD=,OE=OF=1,cos 〈,〉==×(·+·+·+·)=-.
5. B 根据棱台的性质可知A1B1=1,由于A1A⊥平面ABC,AB 平面ABC,AC 平面ABC,故A1A⊥AB,A1A⊥AC.又AB⊥AC,所以AB,AC,AA1两两垂直,故以A为坐标原点,AB,AC,AA1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,平面CC1A的一个法向量为m=(1,0,0),M(1,1,0),C1(0,1,2),即=(1,1,0),=(0,1,2).设平面MAC1的法向量为n=(x,y,z),则故可得平面MAC1的一个法向量为n=(2,-2,1).设二面角M-AC1-C的平面角为θ,由图可知θ为锐角,所以cos θ==.
6. A 设平面EFB与底面ABCD所成的二面角的平面角为θ,由图可得θ不为钝角.以D为坐标原点,建立如图所示的空间直角坐标系,设正方体的棱长为1,则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),E(1,0,m),F(n,1,1),所以=(0,-1,m),=(n-1,0,1).设平面EFB的法向量为n=(x,y,z),则即令x=-1,则y=m(n-1),z=n-1,故n=(-1,m(n-1),n-1).又底面ABCD的一个法向量为m=(0,0,1),所以cos θ=|cos 〈n,m〉|==.因为m,n∈[0,1],所以cos θ=,当n=1时,cos θ=0;当n≠1时,cos θ=,n∈[0,1),m∈[0,1],则(1-n)2∈(0,1],m2∈[0,1],则∈[1,+∞),则当n=0,m=0时,分母取到最小值,此时(cos θ)max=;当n→1,n>0时,则→0,此时cos θ∈(0,].综上,cos θ∈[0,].
7. ACD 取线段AB的中点O,连接CO.在正三棱柱ABC-A1B1C1中,AA1⊥平面ABC.因为△ABC是边长为1的等边三角形,所以CO⊥AB,以O为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,则A(-,0,0),B(,0,0),C(0,,0),A1(-,0,1),B1(,0,1),C1(0,,1),D(0,,).对于A,=(1,0,-1),=(,,),所以·=+0-=0,则A1B⊥AD,故A正确;对于B,设平面AB1D的法向量为m=(x1,y1,z1),=(1,0,1),=(,,),则令x1=1,则z1=-1,y1=0,可得m=(1,0,-1),易知平面A1B1C1的一个法向量为u=(0,0,1),所以cos 〈m,u〉==-=-,所以平面AB1D与平面A1B1C1的夹角为45°,故B错误;对于C,设平面A1BD的法向量为n=(x2,y2,z2),=(1,0,-1),=(,,-),则取x2=1,则z2=1,y2=0,可得n=(1,0,1),则m·n=1+0-1=0,所以m⊥n,故平面A1BD⊥平面AB1D,故C正确;对于D,=(,,0),则cos 〈,m〉===,所以AC与平面AB1D所成的角的正弦值为,故D正确.故选ACD.
8. ABD 以D为坐标原点,DA,DC,DP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设DC=1.对于A,由题意,得A(1,0,0),B(1,1,0),P(0,0,1),E(0,,),所以=(1,0,-1),=(1,1,0),=(0,,).设平面EDB的法向量为m=(x1,y1,z1),则取x1=1,则y1=-1,z1=1,所以m=(1,-1,1),则·m=0.因为PA 平面EDB,所以PA∥平面EDB,故A正确;对于B,=(1,1,-1),因为·=0+-=0,所以PB⊥ED.又EF⊥PB,且EF∩DE=E,EF 平面EFD,DE 平面EFD,所以PB⊥平面EFD,故B正确;对于C,因为侧棱PD⊥底面ABCD,所以∠PBD为直线PB与平面ABCD所成的角.又因为BD==,PB==,所以cos ∠PBD===,故C错误;对于D,由题意,得C(0,1,0),且=(1,0,0),=(0,1,-1).设平面CPB的法向量为n=(x2,y2,z2),则取y2=1,则z2=1,x2=0,所以n=(0,1,1).因为PD⊥底面ABCD,AC 平面ABCD,所以PD⊥AC.因为四边形ABCD是正方形,所以DB⊥AC.又DB∩PD=D,DB 平面PBD,PD 平面PBD,所以AC⊥平面PBD,则平面PBD的一个法向量为=(1,-1,0),所以cos 〈n,〉==-,所以平面CPB与平面PBD的夹角为60°,故D正确.故选ABD.
9. 以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系C-xyz,则C(0,0,0),B1(0,1,2),B(0,1,0),所以1=(0,1,2),=(0,1,0).设AD=a(0≤a≤2),则点D的坐标为(2,0,a),=(2,0,a).设平面B1CD的法向量为m=(x,y,z),则即令z=-1,得m=(,2,-1).又平面C1DC的一个法向量为=(0,1,0),记为n,则由cos 30°===,解得a=(负值舍去),故AD=.
10. 在△ABD和△BC′D中,分别过点A,C′作AM⊥BD,C′N⊥BD,垂足分别为M,N.由S△ABD=AM·BD=AB·AD,代入BD==,AB=,AD=1,得AM==,所以DM===,同理,C′N=,BN=,所以MN=.设二面角A-BD-C′大小为θ(0≤θ≤π),则与夹角为π-θ,由=++,得||2=||2+||2+||2+2·+2·+2·,所以=+++0+2×cos (π-θ)+0,解得cos θ=,所以二面角A-BD-C′的余弦值为.
11. 过点A1在平面A1BD内作A1M⊥BD,垂足为M,过点C在平面BCD内作CN⊥直线BD,垂足为N,如图所示.因为=++,·=·=0,记∠A1BD=α,则α∈(0,),∠NBC=-α,则||=sin α,||=2sin (-α)=2cos α.因为二面角A1-BD-C的大小为,所以,的夹角为.因为·=-·=-||·||cos =-sin αcos α,且||=|||-|||=|2cos (-α)-cos α|=|2sin α-cos α|,所以||2=(++)2=||2+||2+||2+2·=sin 2α+(2sin α-cos α)2+4cos 2α-2sin αcos α=5-3sin 2α≥2,即||≥,当且仅当sin 2α=1,即α=时,等号成立,故线段A1C长度的最小值为.
12. (1) 连接BD.因为AB=AD,∠DAB=60°,所以△ABD是等边三角形.
又E是AD的中点,所以BE⊥AD.
因为PD⊥平面ABCD,BE 平面ABCD,
所以PD⊥BE,又PD∩AD=D,PD 平面PAD,AD 平面PAD,
所以BE⊥平面PAD,又BE 平面PBE,
所以平面PBE⊥平面PAD.
(2) 因为BE⊥平面PAD,所以∠BPE为PB与平面PAD所成的角,即∠BPE=45°.
又PE 平面PAD,所以BE⊥PE.
因为△ABD是边长为2的等边三角形,所以PE=BE=,所以PD==.
以E为坐标原点,建立如图所示的空间直角坐标系,则P(-1,0,),E(0,0,0),C(-2,,0),
所以=(-1,0,),=(-2,,0).
设平面PEC的法向量为m=(x,y,z),
则即
令x=1,得m=(1,,).
因为BE⊥平面PAD,所以n=(0,1,0)为平面PED的一个法向量,
所以cos 〈m,n〉===,
显然二面角C-PE-D为锐角,
所以二面角C-PE-D的余弦值为.
13. (1) 连接A1B,交AB1 于点O.
在正方体ABCD-A1B1C1D1 中,A1B⊥AB1,且BC⊥平面A1B1BA.
因为AB1 平面A1B1BA,
所以BC⊥AB1.
又A1B∩BC=B,A1B 平面A1BC,BC 平面A1BC,
所以AB1⊥平面A1BC.
因为A1C 平面A1BC,
所以AB1⊥A1C,同理B1D1⊥A1C.
又AB1∩B1D1=B1,AB1 平面AB1D1,B1D1 平面AB1D1,
所以A1C⊥平面AB1D1.
设正方体的棱长为1,
则由VA-A1B1D1=VA1-AB1D1,
得××1×1×1=××()2·A1G,
解得A1G=,
同理HC=.
由题意,得A1C=,
所以G,H是线段A1C的三等分点.
(2) 以D为坐标原点,DA,DC,DD1 所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
假设存在点M满足题意,设正方体的棱长为1,则令=m,m∈[0,1],则M(0,m,1),B(1,1,0),A1(1,0,1),C(0,1,0).
由(1)知是平面C1BD的一个法向量,且=(-1,1,-1),=(0,m,1),=(1,1,0).
设平面MBD的法向量为n=(x,y,z),
则即
取y=1,则n=(-1,1,-m).
由cos 60°=,得=,
解得m=-8±3 [0,1],
故棱D1C1 上不存在点M,使得二面角M-BD-C1 的大小为60°.
