小升初复习精讲精练《式与方程》--苏教版(复习课件)
文档属性
| 名称 | 小升初复习精讲精练《式与方程》--苏教版(复习课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-16 16:30:24 | ||
图片预览









文档简介
(共44张PPT)
(苏教版)六年级
下
数与代数
式和方程
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1.能区分、等式与方程的概念。理解方程是“含有未知数的等式”,并举例说明等式的性质。
2.熟练运用“等式性质”解方程,书写过程规范能通过代入检验方程的解是否正确。
3.能从生活情境中抽象出等量关系,用方程解决典型问题,并解释解的合理性。
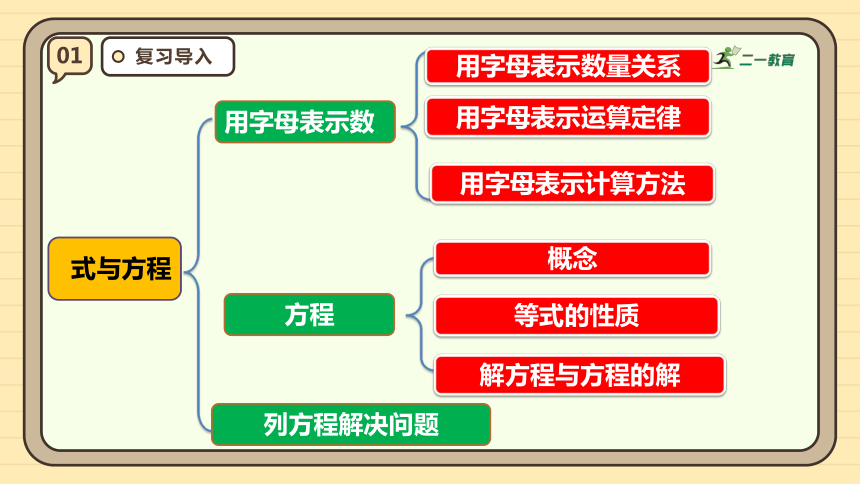
式与方程
用字母表示数
概念
等式的性质
方程
用字母表示数量关系
用字母表示运算定律
用字母表示计算方法
解方程与方程的解
列方程解决问题
01
复习导入
02
任务一
学习任务一
知识梳理
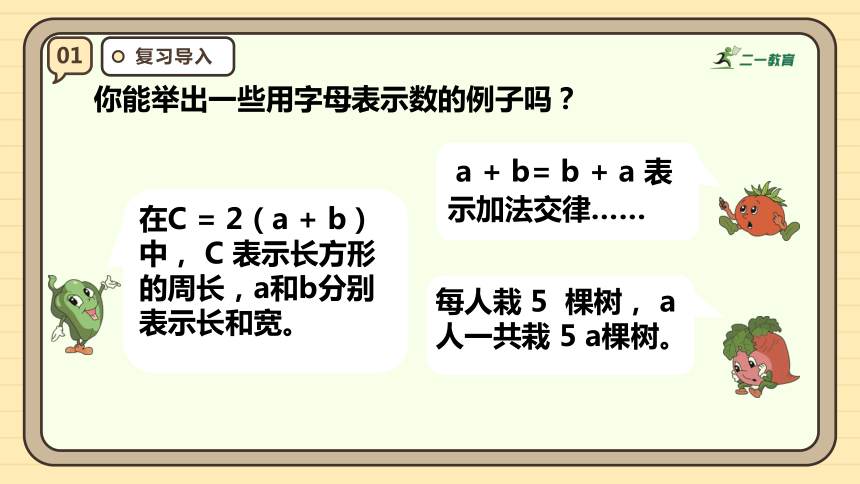
你能举出一些用字母表示数的例子吗?
在C = 2(a + b)中, C 表示长方形的周长,a和b分别表示长和宽。
a + b= b + a 表示加法交律……
每人栽 5 棵树, a 人一共栽 5 a棵树。
01
复习导入
用字母表示数、数量关系
02
知识梳理
用字母表示数:
同一个式子里,同一个字母只能表示同一个数量,同的数不量用不同的字母表示。
用字母表示数量关系:
如速度、时间、路程之间的关系是s=vt。
加法交换律 a+b=b+a
加法结合律 (a+b)+c=a+(b+c)
乘法交换律 ab=ba
乘法结合律 (ab)c=a(bc)
乘法分配律 (a+b)c=ac+bc
02
知识梳理
用字母表示运算律或运算性质
用字母表示计算周长和面积公式
长方形 C=2(a+b) S=ab
正方形 C=4a S=a
圆 C=2πr S=πr2
平行四边形 S=ah
三角形 S=ah÷2
……
02
知识梳理
用字母表示数的写法
在含有字母的乘法算式里,乘号可以省略不写或用“·”表示;加、减和除号都不能省略。
数与字母相乘时,可以省略乘号,一般把数写在字母前面(1与字母相乘时,1可以省略不写);字母与字母相乘时,积一般按字母顺序写出。
两个相同字母相乘时,乘号不能省略,但可以写成这个字母的平方。
02
知识梳理
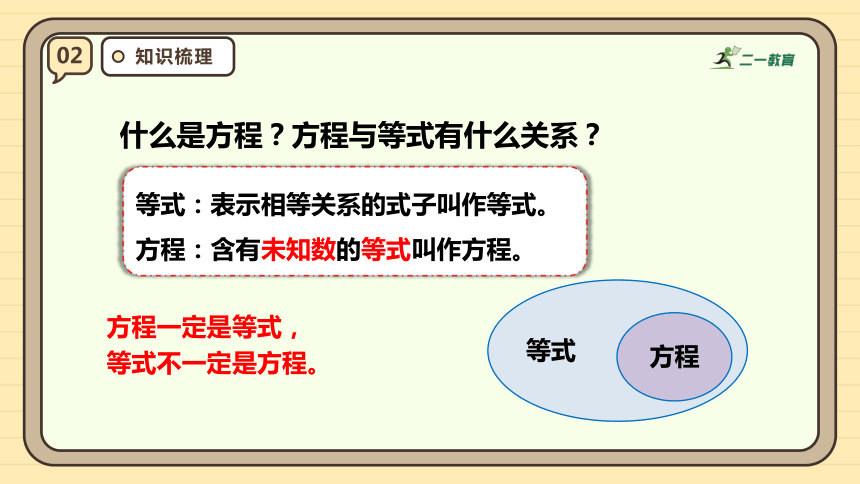
什么是方程?方程与等式有什么关系?
方程一定是等式,
等式不一定是方程。
等式
方程
等式:表示相等关系的式子叫作等式。
方程:含有未知数的等式叫作方程。
02
知识梳理
等式的性质:
性质1:等式的两边同时加上或减去同一个数,等式仍然成立。
性质2:等式两边同时乘或除以同一个数(0除外),等式仍然成立。
若a=b,则a+c=b+c或a c=b c。
若a=b,则ac=bc或a÷c=b÷c。(c≠0)
02
知识梳理
求方程的解的过程叫作解方程。
使方程左右两边相等的未知数的值叫作方程的解。
检验方程的解的方法:
将未知数的值代入方程,看方程的左右两边是否相等。
如果相等,所求的未知数的值就是方程的解,否则就不是。
02
知识梳理
(1)找出未知数,用字母x表示。
(2)分析实际问题中的数量关系,找出等量关系,列方程。
(3)解方程并检验作答。
未知数用字母表示,参与列式运算。
用方程解决问题的一般步骤
用方程解决问题的特点
02
知识梳理
找等量关系解应用题的常用方法
1.根据常见量的数量关系确定等量关系。
2.利用公式确定等式关系。
3.借助线段图确定等量关系。
4.根据题中关键句确定等量关系。
02
知识梳理
03
任务二
学习任务二
典型例题
9a 表示__________________;
58b 表示_________________;
58-a 表示_______________________________;
9a+58b 表示______________________________;
如果a=45,b=6,则9a+58b=____。
9个足球的总价
b个篮球的总价
篮球单价比足球单价贵的价钱
买9个足球和b个篮球的总价
753
足球的数量×单价
篮球的数量×单价
9×45+58×6
1.学校买来9个足球,每个a元;又买来b个篮球,每个58元。
04
例题讲解
(2)已知a=100,b=10,剩余____ t水泥。
2.(1)工地上有a t水泥,如果每天用去2.5 t,用了b 天,剩余____________ t水泥。
(a-2.5b)
75
每天用的吨数×天数=用去的吨数
总吨数-用去的吨数=剩下的吨数
100-2.5×10
04
例题讲解
3.用小棒摆六边形,如下图所示。
六边形的个数 图形 小棒的根数
1
2
3
6
6
+5
6+5
+5
……
……
……
(1)你能发现什么规律?
每增加一个六边形多用5根小棒。
04
例题讲解
六边形的个数 图形 小棒的根数
+5
6+5
1+5+5
6
+5
1+5
1
2
3
6
+5
……
……
……
(2)按这个规律摆n个六边形,需要 ______________ 根小棒。
6+5(n-1)
1
或1+5n
(3)按这个规律摆150个六边形,需要 ____ 根小棒。
1+5×150
751
04
例题讲解
4.解方程。
x+x=42
x=36
=
x=30%×4
x=1.2
解:
解:
04
例题讲解
x=42
7
6
5.全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
设大船x只,则小船(10 x)只
根据大船坐的总人数+小船坐的总人数=全班人数的等量关系列方程
5x+3(10 x)=42
2x=12
x=6
10 x=10 6=4
检验:
5×6+3×4=42(人)
6+4=10(只)
大船6只,小船4只。
04
例题讲解
6.三个连续的自然数,中间的数是a,则a 前边和后边的数
分别是________和________。
a-1
a+1
7.当n 表示所有的自然数0,1,2,3,4,5,…
时,2n 表示什么数?2n+1呢?
答:2n表示偶数,2n+1表示奇数。
04
例题讲解
1.在括号里填写含有字母的式子。
(1)一种贺卡的单价是a元/张,小英买5张,用去( )元;小明买n张,付出10元,应找回( )元。
(2)苹果的单价是6.2元/千克,梨的单价是4.5元/千克。妈妈买了a千克苹果和b千克梨,一共要付( )元。
(3)一个正方形的边长是a米,周长是( )米,面积是( )平方米。当a=3时,正方形的周长是( )米,面积是( )平方米。
5a
10-na
6.2a+4.5b
4a
a
9
12
----变式训练
05
课堂练习
2.解方程。
30x=15
30x÷30=15÷30
16+4x=40
16+4x-16=40-16
4x=24
4x÷4=24÷4
x=24÷4
x=6
x-x=
解:
解:
解:
----变式训练
05
课堂练习
x=
1
2
x=
15
30
x × = ×
5
9
10
21
5
9
5
9
x=
10
21
5
9
x=
6
7
3. 判断
(1)含有未知数的式子叫方程。………………( )
(2)n表示自然数,2n就可以表示偶数。……( )
(3)因为22=2×2,所以a2=a×2。……………( )
(4)56-x<0.7不是方程。………………… ( )
(5)c+c=2c,a×a=2a。……………… … ( )
×
√
×
×
√
----变式训练
05
课堂练习
4.学校食堂里有面粉a千克,每天用去10.5千克,用了b天,
剩下的面粉的质量用式子表示是( )千克。
如果a=100,b=6,那么剩下( )千克。
a-10.5b
37
剩下的面粉质量=原有面粉的质量-用去的质量
用去的质量=每天用去的×用的天数
----变式训练
05
课堂练习
5.一张桌子和一把椅子共144元,一张桌子的价格是
一把椅子的3倍,一张桌子多少元?
解:设一把椅子x 元,则一张桌子是3x元。
x+3x=144
4x=144
x=144÷4
x=36
3×36=108(元/张)
答:一张桌子108元。
----变式训练
05
课堂练习
06
任务四
学习任务四
培优拓展
1.用一条绳子测井的深度,折成3段来测,井外还余5米;
折成4段来测,井外还余2米,这条绳子长多少米?
5米
2米
如果设绳长x米,那么折成3段之后的长为—米,折成4段之后的长为—米;根据井的深度不变列方程解答。
x3
x4
06
培优拓展
5米
2米
解:设这条绳子长x 米。
x=36
答:这条绳子长36米。
1.用一条绳子测井的深度,折成3段来测,井外还余5米;折成4段来测,井外还余2米,这条绳子长多少米?
06
培优拓展
-5= -2
x
3
x
4
- =5-2
x
4
x
3
=3
x
12
2.8条腿的蜘蛛和6条腿的螳螂共有25只。如果它们一共有170条腿,那么蜘蛛和螳螂各有多少只?
06
培优拓展
06
培优拓展
解:设蜘蛛有x只,则螳螂有(25-x)只。
8x+(25-x)×6=170
2x+150=170
2x=20
x=10
螳螂:25-10=15(只)
答:蜘蛛有10只,螳螂有15只。
3.数学家丢番图的墓碑上刻着:“他的童年占去一生的,接着是少年时代,又过了的时光,他找到了终身伴侣。5年以后,婚姻之神赐给他一个儿子,可是儿子命运不济,只活到父亲寿数的一半,就匆匆离去。4年后,父亲也因为过分悲伤而离开人世。”丢番图活了多少岁?
丢番图的一生
1 -
7
1-
2
5年
4年
06
培优拓展
解:设丢番图活了x岁。
x=84
答:丢番图活了84岁。
06
培优拓展
x
6
x
12
x
7
x- - - -5- =4
x
2
x=9
3
28
(1- - - - )x=4+5
1
6
1
7
1
2
1
12
方程是“平衡的天平”:等式两边同步变化(同加同减、同乘同除)才能保持平衡。
字母代表数,关系是关键: 实际问题中,先设未知数再根据题目中的等量关系,列出方程。
这节课你们都学会了哪些知识?
07
课堂小结
1.填空。
(1)学校原有图书7260本,又买来a本,现在共有图书
( )本。
(2)有m吨煤,每次运5吨,需运( )次。
(3)每米花布13.60元, x米需要( )元。
(4)每小时行b千米,3小时行( )千米,
7小时行( )千米。
7260+a
m÷5
13.60 x
3b
7b
08
作业布置
作业布置---知识技能类
2.京沪高速公路全长1260千米。甲、乙两辆汽车同时分别从
北京和上海出发,相向而行,经过6小时相遇。甲车的速度
是90千米/时,乙车的速度是多少?
数量关系式:
路程÷时间=速度
列方程解应用题时要找对等量关系。
08
作业布置
作业布置---知识技能类
解:设乙车速度是xkm/h。
(x+90)×6=1260
6x+540=1260
6x+540-540=1260-540
6x=720
6x÷6=720÷6
x=120
答:乙车速度是120km/h。
08
作业布置
作业布置---知识技能类
3.小芳收集的外国邮票比中国邮票少35张,外国邮票的张数是中国邮票的,小芳收集的外国邮票和中国邮票各多少张?
答:小芳收集的中国邮票有56张,外国邮票有21张。
x=56
08
作业布置
作业布置---知识技能类
x- x =35
3
8
x=35÷
5
8
x=35
5
8
x = ×56=21
3
8
3
8
解:设小芳收集的中国邮票有x张,则外国邮票有 x 张。
3
8
4.学校开展兴趣小组活动,参加书法组的有18人,比美术组的25%少6人,参加美术组的有几人?
解:设参加美术组的有x人。
25x %-6=18
答:参加美术组的有96人。
0.25x=18+6
0.25x=24
x=96
08
作业布置
作业布置---知识技能类
09
板书设计
式 与 方程
1.式:用字母表示数
2.方程:含未知数的等式
3.解方程口诀
天平平衡两边变,逆运算来解谜题
4.应用关键
设未知数→找等量关系→列方程→解→验
https://www.21cnjy.com/recruitment/home/fine
(苏教版)六年级
下
数与代数
式和方程
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1.能区分、等式与方程的概念。理解方程是“含有未知数的等式”,并举例说明等式的性质。
2.熟练运用“等式性质”解方程,书写过程规范能通过代入检验方程的解是否正确。
3.能从生活情境中抽象出等量关系,用方程解决典型问题,并解释解的合理性。
式与方程
用字母表示数
概念
等式的性质
方程
用字母表示数量关系
用字母表示运算定律
用字母表示计算方法
解方程与方程的解
列方程解决问题
01
复习导入
02
任务一
学习任务一
知识梳理
你能举出一些用字母表示数的例子吗?
在C = 2(a + b)中, C 表示长方形的周长,a和b分别表示长和宽。
a + b= b + a 表示加法交律……
每人栽 5 棵树, a 人一共栽 5 a棵树。
01
复习导入
用字母表示数、数量关系
02
知识梳理
用字母表示数:
同一个式子里,同一个字母只能表示同一个数量,同的数不量用不同的字母表示。
用字母表示数量关系:
如速度、时间、路程之间的关系是s=vt。
加法交换律 a+b=b+a
加法结合律 (a+b)+c=a+(b+c)
乘法交换律 ab=ba
乘法结合律 (ab)c=a(bc)
乘法分配律 (a+b)c=ac+bc
02
知识梳理
用字母表示运算律或运算性质
用字母表示计算周长和面积公式
长方形 C=2(a+b) S=ab
正方形 C=4a S=a
圆 C=2πr S=πr2
平行四边形 S=ah
三角形 S=ah÷2
……
02
知识梳理
用字母表示数的写法
在含有字母的乘法算式里,乘号可以省略不写或用“·”表示;加、减和除号都不能省略。
数与字母相乘时,可以省略乘号,一般把数写在字母前面(1与字母相乘时,1可以省略不写);字母与字母相乘时,积一般按字母顺序写出。
两个相同字母相乘时,乘号不能省略,但可以写成这个字母的平方。
02
知识梳理
什么是方程?方程与等式有什么关系?
方程一定是等式,
等式不一定是方程。
等式
方程
等式:表示相等关系的式子叫作等式。
方程:含有未知数的等式叫作方程。
02
知识梳理
等式的性质:
性质1:等式的两边同时加上或减去同一个数,等式仍然成立。
性质2:等式两边同时乘或除以同一个数(0除外),等式仍然成立。
若a=b,则a+c=b+c或a c=b c。
若a=b,则ac=bc或a÷c=b÷c。(c≠0)
02
知识梳理
求方程的解的过程叫作解方程。
使方程左右两边相等的未知数的值叫作方程的解。
检验方程的解的方法:
将未知数的值代入方程,看方程的左右两边是否相等。
如果相等,所求的未知数的值就是方程的解,否则就不是。
02
知识梳理
(1)找出未知数,用字母x表示。
(2)分析实际问题中的数量关系,找出等量关系,列方程。
(3)解方程并检验作答。
未知数用字母表示,参与列式运算。
用方程解决问题的一般步骤
用方程解决问题的特点
02
知识梳理
找等量关系解应用题的常用方法
1.根据常见量的数量关系确定等量关系。
2.利用公式确定等式关系。
3.借助线段图确定等量关系。
4.根据题中关键句确定等量关系。
02
知识梳理
03
任务二
学习任务二
典型例题
9a 表示__________________;
58b 表示_________________;
58-a 表示_______________________________;
9a+58b 表示______________________________;
如果a=45,b=6,则9a+58b=____。
9个足球的总价
b个篮球的总价
篮球单价比足球单价贵的价钱
买9个足球和b个篮球的总价
753
足球的数量×单价
篮球的数量×单价
9×45+58×6
1.学校买来9个足球,每个a元;又买来b个篮球,每个58元。
04
例题讲解
(2)已知a=100,b=10,剩余____ t水泥。
2.(1)工地上有a t水泥,如果每天用去2.5 t,用了b 天,剩余____________ t水泥。
(a-2.5b)
75
每天用的吨数×天数=用去的吨数
总吨数-用去的吨数=剩下的吨数
100-2.5×10
04
例题讲解
3.用小棒摆六边形,如下图所示。
六边形的个数 图形 小棒的根数
1
2
3
6
6
+5
6+5
+5
……
……
……
(1)你能发现什么规律?
每增加一个六边形多用5根小棒。
04
例题讲解
六边形的个数 图形 小棒的根数
+5
6+5
1+5+5
6
+5
1+5
1
2
3
6
+5
……
……
……
(2)按这个规律摆n个六边形,需要 ______________ 根小棒。
6+5(n-1)
1
或1+5n
(3)按这个规律摆150个六边形,需要 ____ 根小棒。
1+5×150
751
04
例题讲解
4.解方程。
x+x=42
x=36
=
x=30%×4
x=1.2
解:
解:
04
例题讲解
x=42
7
6
5.全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
设大船x只,则小船(10 x)只
根据大船坐的总人数+小船坐的总人数=全班人数的等量关系列方程
5x+3(10 x)=42
2x=12
x=6
10 x=10 6=4
检验:
5×6+3×4=42(人)
6+4=10(只)
大船6只,小船4只。
04
例题讲解
6.三个连续的自然数,中间的数是a,则a 前边和后边的数
分别是________和________。
a-1
a+1
7.当n 表示所有的自然数0,1,2,3,4,5,…
时,2n 表示什么数?2n+1呢?
答:2n表示偶数,2n+1表示奇数。
04
例题讲解
1.在括号里填写含有字母的式子。
(1)一种贺卡的单价是a元/张,小英买5张,用去( )元;小明买n张,付出10元,应找回( )元。
(2)苹果的单价是6.2元/千克,梨的单价是4.5元/千克。妈妈买了a千克苹果和b千克梨,一共要付( )元。
(3)一个正方形的边长是a米,周长是( )米,面积是( )平方米。当a=3时,正方形的周长是( )米,面积是( )平方米。
5a
10-na
6.2a+4.5b
4a
a
9
12
----变式训练
05
课堂练习
2.解方程。
30x=15
30x÷30=15÷30
16+4x=40
16+4x-16=40-16
4x=24
4x÷4=24÷4
x=24÷4
x=6
x-x=
解:
解:
解:
----变式训练
05
课堂练习
x=
1
2
x=
15
30
x × = ×
5
9
10
21
5
9
5
9
x=
10
21
5
9
x=
6
7
3. 判断
(1)含有未知数的式子叫方程。………………( )
(2)n表示自然数,2n就可以表示偶数。……( )
(3)因为22=2×2,所以a2=a×2。……………( )
(4)56-x<0.7不是方程。………………… ( )
(5)c+c=2c,a×a=2a。……………… … ( )
×
√
×
×
√
----变式训练
05
课堂练习
4.学校食堂里有面粉a千克,每天用去10.5千克,用了b天,
剩下的面粉的质量用式子表示是( )千克。
如果a=100,b=6,那么剩下( )千克。
a-10.5b
37
剩下的面粉质量=原有面粉的质量-用去的质量
用去的质量=每天用去的×用的天数
----变式训练
05
课堂练习
5.一张桌子和一把椅子共144元,一张桌子的价格是
一把椅子的3倍,一张桌子多少元?
解:设一把椅子x 元,则一张桌子是3x元。
x+3x=144
4x=144
x=144÷4
x=36
3×36=108(元/张)
答:一张桌子108元。
----变式训练
05
课堂练习
06
任务四
学习任务四
培优拓展
1.用一条绳子测井的深度,折成3段来测,井外还余5米;
折成4段来测,井外还余2米,这条绳子长多少米?
5米
2米
如果设绳长x米,那么折成3段之后的长为—米,折成4段之后的长为—米;根据井的深度不变列方程解答。
x3
x4
06
培优拓展
5米
2米
解:设这条绳子长x 米。
x=36
答:这条绳子长36米。
1.用一条绳子测井的深度,折成3段来测,井外还余5米;折成4段来测,井外还余2米,这条绳子长多少米?
06
培优拓展
-5= -2
x
3
x
4
- =5-2
x
4
x
3
=3
x
12
2.8条腿的蜘蛛和6条腿的螳螂共有25只。如果它们一共有170条腿,那么蜘蛛和螳螂各有多少只?
06
培优拓展
06
培优拓展
解:设蜘蛛有x只,则螳螂有(25-x)只。
8x+(25-x)×6=170
2x+150=170
2x=20
x=10
螳螂:25-10=15(只)
答:蜘蛛有10只,螳螂有15只。
3.数学家丢番图的墓碑上刻着:“他的童年占去一生的,接着是少年时代,又过了的时光,他找到了终身伴侣。5年以后,婚姻之神赐给他一个儿子,可是儿子命运不济,只活到父亲寿数的一半,就匆匆离去。4年后,父亲也因为过分悲伤而离开人世。”丢番图活了多少岁?
丢番图的一生
1 -
7
1-
2
5年
4年
06
培优拓展
解:设丢番图活了x岁。
x=84
答:丢番图活了84岁。
06
培优拓展
x
6
x
12
x
7
x- - - -5- =4
x
2
x=9
3
28
(1- - - - )x=4+5
1
6
1
7
1
2
1
12
方程是“平衡的天平”:等式两边同步变化(同加同减、同乘同除)才能保持平衡。
字母代表数,关系是关键: 实际问题中,先设未知数再根据题目中的等量关系,列出方程。
这节课你们都学会了哪些知识?
07
课堂小结
1.填空。
(1)学校原有图书7260本,又买来a本,现在共有图书
( )本。
(2)有m吨煤,每次运5吨,需运( )次。
(3)每米花布13.60元, x米需要( )元。
(4)每小时行b千米,3小时行( )千米,
7小时行( )千米。
7260+a
m÷5
13.60 x
3b
7b
08
作业布置
作业布置---知识技能类
2.京沪高速公路全长1260千米。甲、乙两辆汽车同时分别从
北京和上海出发,相向而行,经过6小时相遇。甲车的速度
是90千米/时,乙车的速度是多少?
数量关系式:
路程÷时间=速度
列方程解应用题时要找对等量关系。
08
作业布置
作业布置---知识技能类
解:设乙车速度是xkm/h。
(x+90)×6=1260
6x+540=1260
6x+540-540=1260-540
6x=720
6x÷6=720÷6
x=120
答:乙车速度是120km/h。
08
作业布置
作业布置---知识技能类
3.小芳收集的外国邮票比中国邮票少35张,外国邮票的张数是中国邮票的,小芳收集的外国邮票和中国邮票各多少张?
答:小芳收集的中国邮票有56张,外国邮票有21张。
x=56
08
作业布置
作业布置---知识技能类
x- x =35
3
8
x=35÷
5
8
x=35
5
8
x = ×56=21
3
8
3
8
解:设小芳收集的中国邮票有x张,则外国邮票有 x 张。
3
8
4.学校开展兴趣小组活动,参加书法组的有18人,比美术组的25%少6人,参加美术组的有几人?
解:设参加美术组的有x人。
25x %-6=18
答:参加美术组的有96人。
0.25x=18+6
0.25x=24
x=96
08
作业布置
作业布置---知识技能类
09
板书设计
式 与 方程
1.式:用字母表示数
2.方程:含未知数的等式
3.解方程口诀
天平平衡两边变,逆运算来解谜题
4.应用关键
设未知数→找等量关系→列方程→解→验
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
