8.1.3.1 三角形的三边关系 课件(共28张PPT)
文档属性
| 名称 | 8.1.3.1 三角形的三边关系 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 16:34:27 | ||
图片预览





文档简介
(共28张PPT)
三角形的三边关系
第一课时:三角形的三边关系
华东师大版 七年级 下册
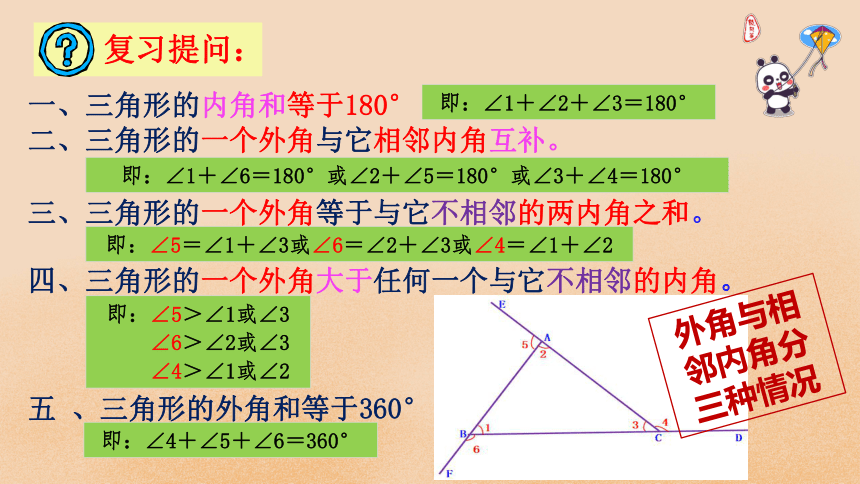
复习提问:
三、三角形的一个外角等于与它不相邻的两内角之和。
四、三角形的一个外角大于任何一个与它不相邻的内角。
一、三角形的内角和等于180°
二、三角形的一个外角与它相邻内角互补。
五 、三角形的外角和等于360°
即:∠1+∠2+∠3=180°
即:∠1+∠6=180°或∠2+∠5=180°或∠3+∠4=180°
即:∠5=∠1+∠3或∠6=∠2+∠3或∠4=∠1+∠2
即:∠5>∠1或∠3
∠6>∠2或∠3
∠4>∠1或∠2
外角与相邻内角分三种情况
即:∠4+∠5+∠6=360°
1、钓鱼神器中的几何模型,若AB∥CD,
∠ABE=132°,∠ADC=65°则∠COD的度数为( )
A.65° B.67° C.60° D.48°
2、比较∠1、∠2、∠B大小,下列结论正确的是( )
A.∠2>∠1>∠B B.∠1>∠B>∠2
C.∠1>∠2>∠B D.∠B>∠2>∠1
3、某中学数学课上,同学们用一张等宽的纸条折成如图所示的图案,若∠1=35°,
则∠2的度数为 。
练一练
B
C
110°
情境导入
是真的吗?CCTV2有一个节目《这是真的吗》,有一期节目是这样的:
说用火柴可以在桌子旁边挂起一瓶矿泉水,问是真的吗?有的嘉宾说不可能,也有些嘉宾说这里有玄机,最后由实验者完成了用三根火柴棍挂起了一瓶矿泉水。
用火柴棍吊起一瓶水,应用了三角形的稳定性。
现实生活中,桥梁设计通常会用到这个性质。学好数学是很有用的!
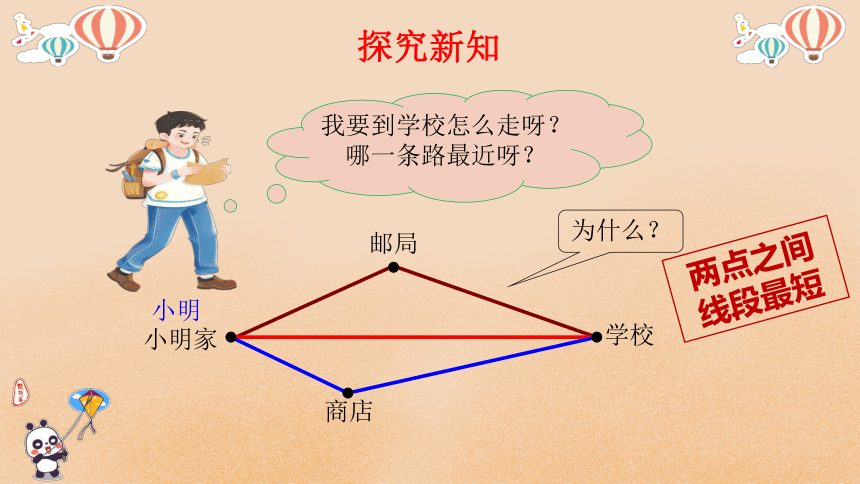
探究新知
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
商店
小明家
小明
两点之间线段最短
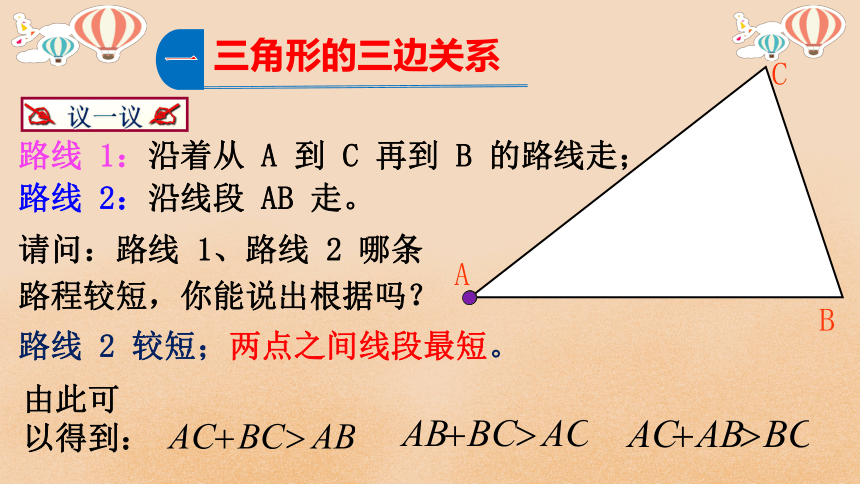
A
B
C
路线 1:沿着从 A 到 C 再到 B 的路线走;
路线 2:沿线段 AB 走。
请问:路线 1、路线 2 哪条路程较短,你能说出根据吗?
路线 2 较短;两点之间线段最短。
由此可以得到:
三角形的三边关系
一
议一议
多
听
多
思
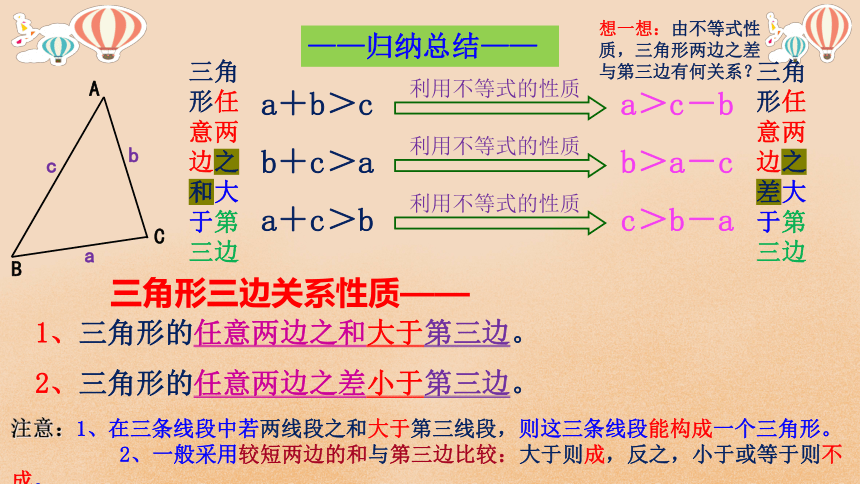
——归纳总结——
a+b>c
b+c>a
a+c>b
a>c-b
b>a-c
c>b-a
A
B
C
a
b
c
利用不等式的性质
利用不等式的性质
利用不等式的性质
三角形任意两边之和大于第三边
三角形任意两边之差大于第三边
想一想:由不等式性质,三角形两边之差与第三边有何关系?
三角形三边关系性质——
2、三角形的任意两边之差小于第三边。
1、三角形的任意两边之和大于第三边。
注意:1、在三条线段中若两线段之和大于第三线段,则这三条线段能构成一个三角形。
2、一般采用较短两边的和与第三边比较:大于则成,反之,小于或等于则不成。
——当堂学会——
例1、下列各组线段中,能组成三角形的是( )
A.4,3,2 B.2,3,5 C.4,4,9 D.3,4,12
方法指导:
已知三条线段,先找到最短的两条线段,
再利用三角形的两边之和大于第三边来判断。
A
例2、如果等腰三角形的一边长是5cm,另一边长是11cm,
求这个等腰三角形的周长。
解:当腰为5cm时,则三边分别为5,5,11。
∵ 5+5<11
∴ 不能组成三角形(不符合题意舍去)
当腰为11cm时,则三边分别为11,11,5。
∵ 5+11>11
∴ 能组成三角形
∴ C=11+11+5=27(cm)
∴ 综上所述,该等腰三角形的周长为27cm。
分类讨论和单位是易错点。
——当堂学会——
(3)3cm、8cm、5cm;
(4)4cm、5cm、6cm;
(1)15cm、10cm、7cm;
(2)4cm、5cm、10cm;
判断下列长度的各组线段能否组成一个三角形?
(5)9cm、9cm、2cm;
7+10>15
能组成三角形
4+5<10
不能组成三角形
3+5=8
不能组成三角形
4+5>6
能组成三角形
2+9>9
能组成三角形
练一练
若一平面上有A、B、C三个点,则:
1、AB+AC BC
2、若AB+AC>BC 则以A、B、C为顶点一定能构成△ABC吗?
≥
A
B
C
想一想
注意:分两种情况考虑:一种是三点不在同一直线上;
另一种是三点在同一条直线上。
不一定
分类讨论:(1)当A、B、C三点不共线时,由三角形任意两边大于第三边知AB+AC>BC
(2)当A、B、C三点共线时,①点A在点B左侧(图1):AB+AC>BC;②点A在点C右侧(图2):AB+AC>BC。③点A在点B与点C中间(图3):AB+AC=BC
分类讨论
三角形边的取值范围
二
a-b<c<a+b
已知三角形两边确定第三边取值范围的方法:
已知两边之差<第三边<已知两边之和
BC-AC<AB<BC+AC
友情提醒——
1、选择两边必须是相同的两边;
2、两边之和选取原则是:较短两边。
例3、已知三角形的两边分别为6、4,求另一边的取值范围?
解:设另一边为x,由三角形三边关系可知:
6-4<x<6+4 解得:2<x<10
∴ 另一边的取值范围是2<x<10。
知两边求第三边
用三边关系求解
——例题讲解——
变式:已知三角形三边长分别为5、x-1、8,则三角形周长C的取值范围是 。
解:由三角形三边关系可知:
8-5<x-1<8+5 解得:4<x<14
∵ C=5+8+x-1=12+x
∴ 周长的范围是:16<12+x<26
两边同时+12
16<C<26
例4、在△ABC中:AC=5,BC=2,AB是奇数且是整数,求△ABC的周长?并判断三角形的形状?
——例题讲解——
解:由三角形三边关系可知:
AC-BC<AB<AC+BC
∵ AC=5 BC=2
∴ 5-2<AB<5+2 解得:3<AB<7
∵ AB是奇数且是整数
∴ AB=5
∴ C△ABC=5+2+5=12 形状是等腰三角形
——例题讲解——
例5、若一个等腰三角形的周长为18cm。
(1)腰长的3倍比底边的2倍多6cm,求各边的长。
(2)已知其中一边的长为4cm,求各边的长。
(3)已知其中一边的长为5cm,求各边的长。
解:(1)设腰为x,底为y,由题意可知:
3x=2y+6 x=6
2x+y=18 解得:y=6
∴ 三边分别为6cm、6cm、6cm。
(2)当4cm是腰时,则底是18-4-4=10(cm)
∵ 4+4<10(不符合题意)
∴ 此种情况不存在。
当4cm是底时,则腰是(18-4)÷2=6(cm)
∵ 4+6>6(符合题意)
∴ 三边分别为4cm、6cm、6cm。
(3)当腰是5cm时,则底是18-5-5=8(cm)
∵ 5+5>8(符合题意)
∴ 三边分别为5cm、5cm、8cm。
当底是5cm时,则腰是(18-5)÷2=6.5(cm)
∵ 5+6.5>6.5(符合题意)
∴ 三边分别为5cm、6.5cm、6.5cm。
练一练
1、若一个等腰三角形的已知两边分别为8cm与5cm,求周长。
(提示:一种考虑8、8、5;另一种考虑5、5、8。)
(周长为21cm或18cm)
2、若一个等腰三角形的已知两边分别为8cm与3cm,求周长。
(提示:一种考虑8、3、3;另一种考虑8、8、3。)
(周长为14cm)
注意:计算等腰三角形周长或三边时,一定要考虑三边能否成一个三角形。
例6、如图,O为△ABC内一点。试证明:
证明:由三角形的三边关系可知:
在△ABO中:AO+BO>AB ①
在△ACO中:AO+CO>AC ②
在△BCO中:BO+CO>BC ③
由①+②+③得:
AO+BO+AO+CO+BO+CO>AB+AC+BC
即:2(AO+BO+CO)>AB+AC+BC
∴ AO+BO+CO>0.5(AB+AC+BC)
——难点突破——
思考:
这些
建筑
物当
中都
有那
些相
似之
处 ?
请同学们观察下面两幅图片:
再观察下面的图形:
想:为什么都用三角形图形 ?
一
想
三角形的稳定性
三
如图,盖房子时,在木框未安装好之前,木工师傅常常先在木框上斜钉一根木条,为什么要这样做呢?
归纳:三角形形状与大小不会改变,四边形形状会改变,这就是说:三角形具有稳定性,四边形不具有稳定性。
理解“稳定性”
三角形的稳定性不是“拉得动、拉不动”的问题,
其实质应是“三角形边长确定,其形状和大小就确定了”。
经验分享归纳——
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”。
例7、要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形使它保持形状,那么要使五边形、六边形木架、七边形木架保持稳定该怎么办呢
——例题讲解——
五边形需要2条
六边形需要3条
七边形需要4条
n边形需要(n-2)
1、下列图形中具有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
2、想想:要使下列木架稳定各至少需要多少根木棍?
3、下列图中具有稳定性有( )
A.1个 B.2个 C.3个 D.4个
C
C
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
不具有稳定性
具有稳定性
练一练
三角形的三边关系
三角形的三边关系:任何两边的和大于第三边,任何两边的差小于第三边。
应用
稳定性
三角形
独有性质
应用
课堂小结
1、判断三条已知线段能否组成三角形的方法:
一种用两条较短边的和与最长边比较:大则能;小或等则不能。
已知两边之差<第三边<已知两边之和
2、已知三角形两边确定第三边取值范围的方法:
3、当等腰三角形腰与底不确定时,要计算周长或边长应注意:
一要分两种情况计算或讨论;
二要看看所求三边能否构成一个三角形。
二种用两条较长边的差与最短边比较:小则能;大或等则不能。
1、从课后习题中选取;
2、完成练习册本课时的习题。
课后作业
谢谢欣赏
THANK YOU FOR LISTENING
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
三角形的三边关系
第一课时:三角形的三边关系
华东师大版 七年级 下册
复习提问:
三、三角形的一个外角等于与它不相邻的两内角之和。
四、三角形的一个外角大于任何一个与它不相邻的内角。
一、三角形的内角和等于180°
二、三角形的一个外角与它相邻内角互补。
五 、三角形的外角和等于360°
即:∠1+∠2+∠3=180°
即:∠1+∠6=180°或∠2+∠5=180°或∠3+∠4=180°
即:∠5=∠1+∠3或∠6=∠2+∠3或∠4=∠1+∠2
即:∠5>∠1或∠3
∠6>∠2或∠3
∠4>∠1或∠2
外角与相邻内角分三种情况
即:∠4+∠5+∠6=360°
1、钓鱼神器中的几何模型,若AB∥CD,
∠ABE=132°,∠ADC=65°则∠COD的度数为( )
A.65° B.67° C.60° D.48°
2、比较∠1、∠2、∠B大小,下列结论正确的是( )
A.∠2>∠1>∠B B.∠1>∠B>∠2
C.∠1>∠2>∠B D.∠B>∠2>∠1
3、某中学数学课上,同学们用一张等宽的纸条折成如图所示的图案,若∠1=35°,
则∠2的度数为 。
练一练
B
C
110°
情境导入
是真的吗?CCTV2有一个节目《这是真的吗》,有一期节目是这样的:
说用火柴可以在桌子旁边挂起一瓶矿泉水,问是真的吗?有的嘉宾说不可能,也有些嘉宾说这里有玄机,最后由实验者完成了用三根火柴棍挂起了一瓶矿泉水。
用火柴棍吊起一瓶水,应用了三角形的稳定性。
现实生活中,桥梁设计通常会用到这个性质。学好数学是很有用的!
探究新知
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
商店
小明家
小明
两点之间线段最短
A
B
C
路线 1:沿着从 A 到 C 再到 B 的路线走;
路线 2:沿线段 AB 走。
请问:路线 1、路线 2 哪条路程较短,你能说出根据吗?
路线 2 较短;两点之间线段最短。
由此可以得到:
三角形的三边关系
一
议一议
多
听
多
思
——归纳总结——
a+b>c
b+c>a
a+c>b
a>c-b
b>a-c
c>b-a
A
B
C
a
b
c
利用不等式的性质
利用不等式的性质
利用不等式的性质
三角形任意两边之和大于第三边
三角形任意两边之差大于第三边
想一想:由不等式性质,三角形两边之差与第三边有何关系?
三角形三边关系性质——
2、三角形的任意两边之差小于第三边。
1、三角形的任意两边之和大于第三边。
注意:1、在三条线段中若两线段之和大于第三线段,则这三条线段能构成一个三角形。
2、一般采用较短两边的和与第三边比较:大于则成,反之,小于或等于则不成。
——当堂学会——
例1、下列各组线段中,能组成三角形的是( )
A.4,3,2 B.2,3,5 C.4,4,9 D.3,4,12
方法指导:
已知三条线段,先找到最短的两条线段,
再利用三角形的两边之和大于第三边来判断。
A
例2、如果等腰三角形的一边长是5cm,另一边长是11cm,
求这个等腰三角形的周长。
解:当腰为5cm时,则三边分别为5,5,11。
∵ 5+5<11
∴ 不能组成三角形(不符合题意舍去)
当腰为11cm时,则三边分别为11,11,5。
∵ 5+11>11
∴ 能组成三角形
∴ C=11+11+5=27(cm)
∴ 综上所述,该等腰三角形的周长为27cm。
分类讨论和单位是易错点。
——当堂学会——
(3)3cm、8cm、5cm;
(4)4cm、5cm、6cm;
(1)15cm、10cm、7cm;
(2)4cm、5cm、10cm;
判断下列长度的各组线段能否组成一个三角形?
(5)9cm、9cm、2cm;
7+10>15
能组成三角形
4+5<10
不能组成三角形
3+5=8
不能组成三角形
4+5>6
能组成三角形
2+9>9
能组成三角形
练一练
若一平面上有A、B、C三个点,则:
1、AB+AC BC
2、若AB+AC>BC 则以A、B、C为顶点一定能构成△ABC吗?
≥
A
B
C
想一想
注意:分两种情况考虑:一种是三点不在同一直线上;
另一种是三点在同一条直线上。
不一定
分类讨论:(1)当A、B、C三点不共线时,由三角形任意两边大于第三边知AB+AC>BC
(2)当A、B、C三点共线时,①点A在点B左侧(图1):AB+AC>BC;②点A在点C右侧(图2):AB+AC>BC。③点A在点B与点C中间(图3):AB+AC=BC
分类讨论
三角形边的取值范围
二
a-b<c<a+b
已知三角形两边确定第三边取值范围的方法:
已知两边之差<第三边<已知两边之和
BC-AC<AB<BC+AC
友情提醒——
1、选择两边必须是相同的两边;
2、两边之和选取原则是:较短两边。
例3、已知三角形的两边分别为6、4,求另一边的取值范围?
解:设另一边为x,由三角形三边关系可知:
6-4<x<6+4 解得:2<x<10
∴ 另一边的取值范围是2<x<10。
知两边求第三边
用三边关系求解
——例题讲解——
变式:已知三角形三边长分别为5、x-1、8,则三角形周长C的取值范围是 。
解:由三角形三边关系可知:
8-5<x-1<8+5 解得:4<x<14
∵ C=5+8+x-1=12+x
∴ 周长的范围是:16<12+x<26
两边同时+12
16<C<26
例4、在△ABC中:AC=5,BC=2,AB是奇数且是整数,求△ABC的周长?并判断三角形的形状?
——例题讲解——
解:由三角形三边关系可知:
AC-BC<AB<AC+BC
∵ AC=5 BC=2
∴ 5-2<AB<5+2 解得:3<AB<7
∵ AB是奇数且是整数
∴ AB=5
∴ C△ABC=5+2+5=12 形状是等腰三角形
——例题讲解——
例5、若一个等腰三角形的周长为18cm。
(1)腰长的3倍比底边的2倍多6cm,求各边的长。
(2)已知其中一边的长为4cm,求各边的长。
(3)已知其中一边的长为5cm,求各边的长。
解:(1)设腰为x,底为y,由题意可知:
3x=2y+6 x=6
2x+y=18 解得:y=6
∴ 三边分别为6cm、6cm、6cm。
(2)当4cm是腰时,则底是18-4-4=10(cm)
∵ 4+4<10(不符合题意)
∴ 此种情况不存在。
当4cm是底时,则腰是(18-4)÷2=6(cm)
∵ 4+6>6(符合题意)
∴ 三边分别为4cm、6cm、6cm。
(3)当腰是5cm时,则底是18-5-5=8(cm)
∵ 5+5>8(符合题意)
∴ 三边分别为5cm、5cm、8cm。
当底是5cm时,则腰是(18-5)÷2=6.5(cm)
∵ 5+6.5>6.5(符合题意)
∴ 三边分别为5cm、6.5cm、6.5cm。
练一练
1、若一个等腰三角形的已知两边分别为8cm与5cm,求周长。
(提示:一种考虑8、8、5;另一种考虑5、5、8。)
(周长为21cm或18cm)
2、若一个等腰三角形的已知两边分别为8cm与3cm,求周长。
(提示:一种考虑8、3、3;另一种考虑8、8、3。)
(周长为14cm)
注意:计算等腰三角形周长或三边时,一定要考虑三边能否成一个三角形。
例6、如图,O为△ABC内一点。试证明:
证明:由三角形的三边关系可知:
在△ABO中:AO+BO>AB ①
在△ACO中:AO+CO>AC ②
在△BCO中:BO+CO>BC ③
由①+②+③得:
AO+BO+AO+CO+BO+CO>AB+AC+BC
即:2(AO+BO+CO)>AB+AC+BC
∴ AO+BO+CO>0.5(AB+AC+BC)
——难点突破——
思考:
这些
建筑
物当
中都
有那
些相
似之
处 ?
请同学们观察下面两幅图片:
再观察下面的图形:
想:为什么都用三角形图形 ?
一
想
三角形的稳定性
三
如图,盖房子时,在木框未安装好之前,木工师傅常常先在木框上斜钉一根木条,为什么要这样做呢?
归纳:三角形形状与大小不会改变,四边形形状会改变,这就是说:三角形具有稳定性,四边形不具有稳定性。
理解“稳定性”
三角形的稳定性不是“拉得动、拉不动”的问题,
其实质应是“三角形边长确定,其形状和大小就确定了”。
经验分享归纳——
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”。
例7、要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形使它保持形状,那么要使五边形、六边形木架、七边形木架保持稳定该怎么办呢
——例题讲解——
五边形需要2条
六边形需要3条
七边形需要4条
n边形需要(n-2)
1、下列图形中具有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
2、想想:要使下列木架稳定各至少需要多少根木棍?
3、下列图中具有稳定性有( )
A.1个 B.2个 C.3个 D.4个
C
C
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
不具有稳定性
具有稳定性
练一练
三角形的三边关系
三角形的三边关系:任何两边的和大于第三边,任何两边的差小于第三边。
应用
稳定性
三角形
独有性质
应用
课堂小结
1、判断三条已知线段能否组成三角形的方法:
一种用两条较短边的和与最长边比较:大则能;小或等则不能。
已知两边之差<第三边<已知两边之和
2、已知三角形两边确定第三边取值范围的方法:
3、当等腰三角形腰与底不确定时,要计算周长或边长应注意:
一要分两种情况计算或讨论;
二要看看所求三边能否构成一个三角形。
二种用两条较长边的差与最短边比较:小则能;大或等则不能。
1、从课后习题中选取;
2、完成练习册本课时的习题。
课后作业
谢谢欣赏
THANK YOU FOR LISTENING
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
