5.4.3 正切函数的性质与图象 课件(共14张PPT)2024-2025学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 5.4.3 正切函数的性质与图象 课件(共14张PPT)2024-2025学年高一上学期数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 312.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-19 06:49:54 | ||
图片预览






文档简介
(共14张PPT)
正切函数的性质与图象
学习目标:
1、掌握利用正切线画正切函数图象的方法
2、能够利用正切函数图象准确归纳其性质并能简单地应用
3、体会数学思想:数形结合类比思想讨论
2、周期性
tan(x+π)=tanx,x≠π/2+kπ,k∈Z
正切函数是周期函数,周期T= π
1、正切函数定义域
3、奇偶性
tan(-x)=-tanx,x∈R,x≠π/2+kπ ,k∈Z
正切函数是奇函数,原点(0,0)是其对称中心
一、正切函数的性质
画出下列各角的正切线:
4、单调性
温故而知新
(0,π/2)时,角改变时,正切怎样变化?其他区间呢?
5、值域
正切函数的值域是实数集R.
二、正切函数的图象
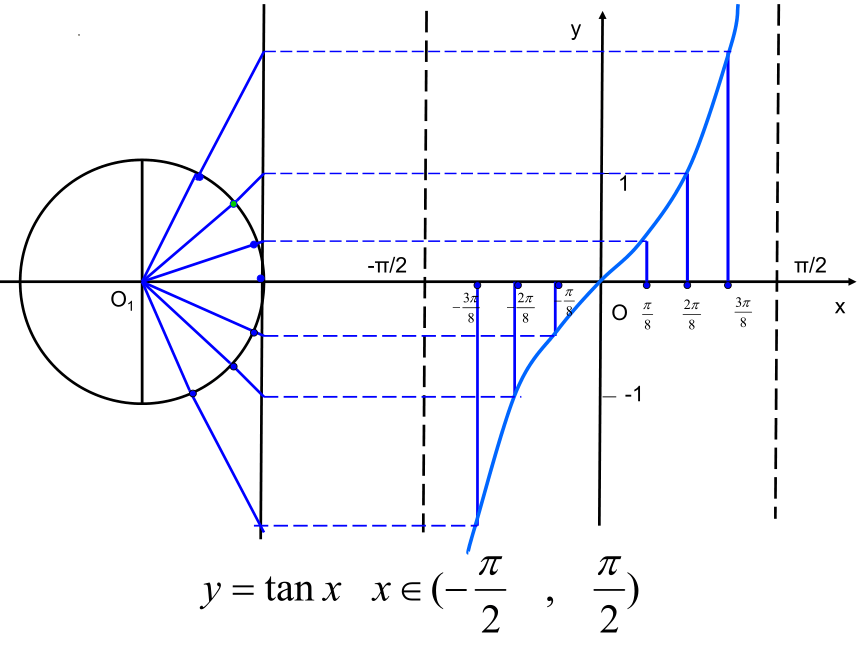
探究,如何通过正切线作出正切函数的图 象??
1、根据正切函数的定义域和周期,
取 x∈ (-π/2,π/2) ,先画函数y=tanx 在
(-π/2,π/2)一个周期上的图象 。
O1
1
-1
O
y
x
-π/2
π/2
2、 把y=tanx,x∈ (-π/2,π/2)图象向左或者
向右平移,每次平移π个单位长度就得到y=tanx
x∈R,且x≠π/2+kπ,k∈Z 的图象。
O
y
x
1
-1
正切函数的图象叫正切曲线,其特征是:
1、被相互平行的直线 x=π/2+kπ,k∈Z
所隔开的无穷多支曲线组成的。
O
π/2
-π/2
-3π/2
3π/2
π
-π
y
x
-π/4
π/4
1
-1
正切曲线的简图的画法:
“三点两线法”
请看在(-π/2,π/2)三点两线在图中的位置。
例6.求函数 的定义域.周期.单调区间.
奇偶性.对称中心。
解(1)原函数要有意义,自变量x应满足
所以,原函数的定义域是
得 T=2 所以原函数的周期是2.
(3)由
所以原函数的单调递增区间是
解得
1.正切函数 的性质:
定义域:
值域:
周期性:
正切函数是周期函数,
周期是
奇偶性:
奇函数
单调性:
在
内是增函数
x
y
o
对称性:
对称中心是
正切函数的性质和图象
小结回顾
课后作业
1.书本P45练习,做书上.
2.P46习题A组6,7,8,9;B组2 做练习本上
谢谢指导
再见
正切函数的性质与图象
学习目标:
1、掌握利用正切线画正切函数图象的方法
2、能够利用正切函数图象准确归纳其性质并能简单地应用
3、体会数学思想:数形结合类比思想讨论
2、周期性
tan(x+π)=tanx,x≠π/2+kπ,k∈Z
正切函数是周期函数,周期T= π
1、正切函数定义域
3、奇偶性
tan(-x)=-tanx,x∈R,x≠π/2+kπ ,k∈Z
正切函数是奇函数,原点(0,0)是其对称中心
一、正切函数的性质
画出下列各角的正切线:
4、单调性
温故而知新
(0,π/2)时,角改变时,正切怎样变化?其他区间呢?
5、值域
正切函数的值域是实数集R.
二、正切函数的图象
探究,如何通过正切线作出正切函数的图 象??
1、根据正切函数的定义域和周期,
取 x∈ (-π/2,π/2) ,先画函数y=tanx 在
(-π/2,π/2)一个周期上的图象 。
O1
1
-1
O
y
x
-π/2
π/2
2、 把y=tanx,x∈ (-π/2,π/2)图象向左或者
向右平移,每次平移π个单位长度就得到y=tanx
x∈R,且x≠π/2+kπ,k∈Z 的图象。
O
y
x
1
-1
正切函数的图象叫正切曲线,其特征是:
1、被相互平行的直线 x=π/2+kπ,k∈Z
所隔开的无穷多支曲线组成的。
O
π/2
-π/2
-3π/2
3π/2
π
-π
y
x
-π/4
π/4
1
-1
正切曲线的简图的画法:
“三点两线法”
请看在(-π/2,π/2)三点两线在图中的位置。
例6.求函数 的定义域.周期.单调区间.
奇偶性.对称中心。
解(1)原函数要有意义,自变量x应满足
所以,原函数的定义域是
得 T=2 所以原函数的周期是2.
(3)由
所以原函数的单调递增区间是
解得
1.正切函数 的性质:
定义域:
值域:
周期性:
正切函数是周期函数,
周期是
奇偶性:
奇函数
单调性:
在
内是增函数
x
y
o
对称性:
对称中心是
正切函数的性质和图象
小结回顾
课后作业
1.书本P45练习,做书上.
2.P46习题A组6,7,8,9;B组2 做练习本上
谢谢指导
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
