5.6 二次函数的图象与一元二次方程 课件(共15张PPT) 2024—2025年青岛版数学九年级下册
文档属性
| 名称 | 5.6 二次函数的图象与一元二次方程 课件(共15张PPT) 2024—2025年青岛版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 06:10:54 | ||
图片预览




文档简介
(共15张PPT)
第5章 对函数的再探索
5.6 二次函数的图象与一元二次方程
情 境 导 入
1.一次函数y=2x-4与x轴的交点坐标是( , )
2.说一说,你是怎样得到的?
2
0
令y=0代入函数解析式即可.
3.怎样求二次函数y=x2-2x-3与x轴的交点?
5.6 二次函数的图象与一元二次方程
新 课 探 究
相等
(1)抛物线与x轴有几个公共点?公共点的坐标分别是什么?
观察抛物线y=x2-2x-3,思考下面的问题:
(2)当x取何值时,函数y=x2-2x-3的值是0?
(3)一元二次方程x2-2x-3=0有没有如果有根它的根是什么?
(4)一元二次方程x2-2x-3=0的根和抛物线y=x2-2x-3与x轴的公共点的横坐标有什么关系?
抛物线与x轴有两个公共点(-1,0),(3,0).
.
.
当x=-1,x=3时,函数y的值是0.即x2-2x-3=0.
一元二次方程x2-2x-3=0的根是x1=-1,x2=3.
.
.
.
探究
5.6 二次函数的图象与一元二次方程
.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
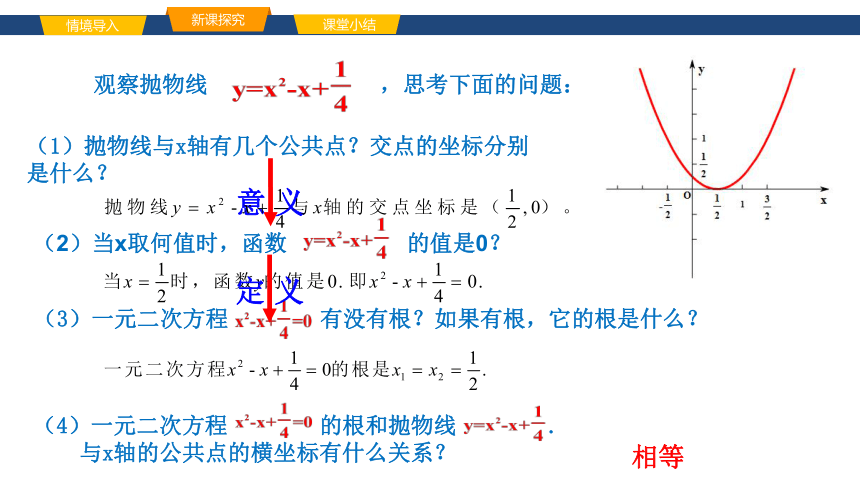
(1)抛物线与x轴有几个公共点?交点的坐标分别
是什么?
观察抛物线 ,思考下面的问题:
(2)当x取何值时,函数 的值是0?
(3)一元二次方程 有没有根?如果有根,它的根是什么?
(4)一元二次方程 的根和抛物线 .
与x轴的公共点的横坐标有什么关系?
定 义
意 义
.
.
相等
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
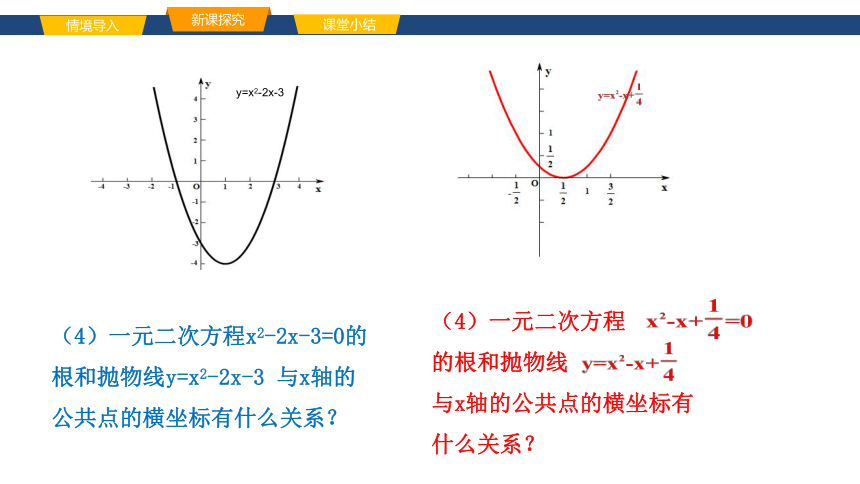
y=x2-2x-3
(4)一元二次方程x2-2x-3=0的
根和抛物线y=x2-2x-3 与x轴的
公共点的横坐标有什么关系?
(4)一元二次方程 的根和抛物线 与x轴的公共点的横坐标有什么关系?
新课探究
情境导入
课堂小结
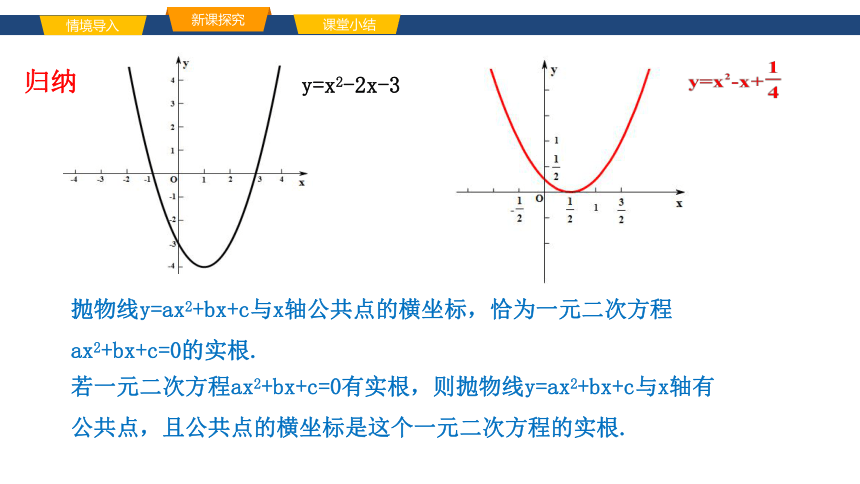
抛物线y=ax2+bx+c与x轴公共点的横坐标,恰为一元二次方程ax2+bx+c=0的实根.
若一元二次方程ax2+bx+c=0有实根,则抛物线y=ax2+bx+c与x轴有公共点,且公共点的横坐标是这个一元二次方程的实根.
y=x2-2x-3
归纳
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例1
用图象法讨论一元二次方程x2-3x-2=0的根.
解:
(1)画抛物线y=x2-3x-2.
(2)由图象可知,在-1与0 之间以及 3与4之间各有一个根.
分别计算x=0,x=-1,x=-0.5的函数值,列表如下:
x
y
-1
-0.5
0
2
-0.25
-2
由于当x=-1时,y>0,当x=-0.5时,y<0,所以方程的根在-1和-0.5之间.
由于在画图和观察过程中
存在误差,所以得到的往往
是二次方程根的近似值
(精确到0.1)
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
可再将-1和-0.5之间分为5等份,每个分点作为x值,利用计算器求出所对应的函数值,列表:
x
y
-1.0
-0.7
-0.9
-0.8
2
-0.5
-0.6
1.04
1.51
0.16
0.59
-0.25
可以看出,这个根在-0.6和-0.5之间,由于本题要求精确到0.1,所以可以将-0.6或-0.5看作二次方程
x2-3x-2=0较小根的近似值,即二次方程x2-3x-2=0的较小根为x≈-0.6或x≈-0.5.
你能求出二次方程x2-3x-2=0较大根
的近似值吗?试试看!
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
同样的,可以求出一元二次方程x2-3x-2=0的较大根的近似值,列表如下:
由上表可见,方程的较大根在3.5和3.6之间,
所以可以将3.5或3.6看作二次方程x2-3x-2=0较大根的近似值,即二次方程x2-3x-2=0的较大根为x≈3.5或x≈3.6.
3.0
-0.25
-2
0.16
3.7
3.6
3.5
1.04
0.59
3.9
3.8
2
1.51
4.0
x
y
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例2 用图象法讨论一元二次方程x2-2x+3=0的根.
x
y
解:
(1)画出抛物线y=x2-2x+3.
(2)由于图象与x轴没有公共点,
所以一元二次方程x2-2x+3=0没有实数根.
抛物线y=ax2+bx+c
与x轴无公共点
二次方程ax2+bx+c=0无实根
转化为
单击此处添加标题文本内容
挑战自我
已知抛物线y=ax2+bx+c.当a,b,c满足什么条件时,
(1)抛物线与x轴有两个公共点?
(2)抛物线与x轴只有一个公共点?
(3)抛物线与x轴没有公共点?
二次方程ax2+bx+c=0中Δ>0
二次方程ax2+bx+c=0中Δ=0
二次方程ax2+bx+c=0中Δ<0
新课探究
情境导入
课堂小结
单击此处添加标题文本内容
抛物线y=ax2+bx+c
与x轴有公共点
二次方程ax2+bx+c=0
有实根
二次方程ax2+bx+c=0
的根的判别式Δ≥ 0
转化为
为化转
转化为
为化转
转化为
新课探究
情境导入
课堂小结
抛物线y=ax2+bx+c
与x轴无公共点
二次方程ax2+bx+c=0
无实根
二次方程ax2+bx+c=0
的根的判别式Δ<0
转化为
为化转
转化为
为化转
转化为
新课探究
情境导入
课堂小结
单击此处添加标题文本内容
课堂检测:
2、如果关于x的一元二次方程x2-2x+m=0有两个相等的实数根,则m= ,此时抛物线y=x2-2x+m与x轴有 个公共点.
1、二次方程x2+x-6=0的两根为x1=-3,x2=2,则二次函数y=x2+x-6的图象与x轴公共点的坐标为 .
(-3,0),(2,0)
1
1
新课探究
情境导入
课堂小结
课 堂 小 结
二次函数y=ax2+bx+c的图象与一元二次方程 ax2+bx+c=0的关系.
二次函数y=ax2+bx+c的图象
二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象与x轴公共点个数
二次方程ax2+bx+c=0的根的判别式
两个公共点
一个公共点
没有公共点
有两个不等实根
有两个相等实根
没有实根
=0
>0
<0
5.6 二次函数的图象与一元二次方程
第5章 对函数的再探索
5.6 二次函数的图象与一元二次方程
情 境 导 入
1.一次函数y=2x-4与x轴的交点坐标是( , )
2.说一说,你是怎样得到的?
2
0
令y=0代入函数解析式即可.
3.怎样求二次函数y=x2-2x-3与x轴的交点?
5.6 二次函数的图象与一元二次方程
新 课 探 究
相等
(1)抛物线与x轴有几个公共点?公共点的坐标分别是什么?
观察抛物线y=x2-2x-3,思考下面的问题:
(2)当x取何值时,函数y=x2-2x-3的值是0?
(3)一元二次方程x2-2x-3=0有没有如果有根它的根是什么?
(4)一元二次方程x2-2x-3=0的根和抛物线y=x2-2x-3与x轴的公共点的横坐标有什么关系?
抛物线与x轴有两个公共点(-1,0),(3,0).
.
.
当x=-1,x=3时,函数y的值是0.即x2-2x-3=0.
一元二次方程x2-2x-3=0的根是x1=-1,x2=3.
.
.
.
探究
5.6 二次函数的图象与一元二次方程
.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
(1)抛物线与x轴有几个公共点?交点的坐标分别
是什么?
观察抛物线 ,思考下面的问题:
(2)当x取何值时,函数 的值是0?
(3)一元二次方程 有没有根?如果有根,它的根是什么?
(4)一元二次方程 的根和抛物线 .
与x轴的公共点的横坐标有什么关系?
定 义
意 义
.
.
相等
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
y=x2-2x-3
(4)一元二次方程x2-2x-3=0的
根和抛物线y=x2-2x-3 与x轴的
公共点的横坐标有什么关系?
(4)一元二次方程 的根和抛物线 与x轴的公共点的横坐标有什么关系?
新课探究
情境导入
课堂小结
抛物线y=ax2+bx+c与x轴公共点的横坐标,恰为一元二次方程ax2+bx+c=0的实根.
若一元二次方程ax2+bx+c=0有实根,则抛物线y=ax2+bx+c与x轴有公共点,且公共点的横坐标是这个一元二次方程的实根.
y=x2-2x-3
归纳
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例1
用图象法讨论一元二次方程x2-3x-2=0的根.
解:
(1)画抛物线y=x2-3x-2.
(2)由图象可知,在-1与0 之间以及 3与4之间各有一个根.
分别计算x=0,x=-1,x=-0.5的函数值,列表如下:
x
y
-1
-0.5
0
2
-0.25
-2
由于当x=-1时,y>0,当x=-0.5时,y<0,所以方程的根在-1和-0.5之间.
由于在画图和观察过程中
存在误差,所以得到的往往
是二次方程根的近似值
(精确到0.1)
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
可再将-1和-0.5之间分为5等份,每个分点作为x值,利用计算器求出所对应的函数值,列表:
x
y
-1.0
-0.7
-0.9
-0.8
2
-0.5
-0.6
1.04
1.51
0.16
0.59
-0.25
可以看出,这个根在-0.6和-0.5之间,由于本题要求精确到0.1,所以可以将-0.6或-0.5看作二次方程
x2-3x-2=0较小根的近似值,即二次方程x2-3x-2=0的较小根为x≈-0.6或x≈-0.5.
你能求出二次方程x2-3x-2=0较大根
的近似值吗?试试看!
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
同样的,可以求出一元二次方程x2-3x-2=0的较大根的近似值,列表如下:
由上表可见,方程的较大根在3.5和3.6之间,
所以可以将3.5或3.6看作二次方程x2-3x-2=0较大根的近似值,即二次方程x2-3x-2=0的较大根为x≈3.5或x≈3.6.
3.0
-0.25
-2
0.16
3.7
3.6
3.5
1.04
0.59
3.9
3.8
2
1.51
4.0
x
y
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例2 用图象法讨论一元二次方程x2-2x+3=0的根.
x
y
解:
(1)画出抛物线y=x2-2x+3.
(2)由于图象与x轴没有公共点,
所以一元二次方程x2-2x+3=0没有实数根.
抛物线y=ax2+bx+c
与x轴无公共点
二次方程ax2+bx+c=0无实根
转化为
单击此处添加标题文本内容
挑战自我
已知抛物线y=ax2+bx+c.当a,b,c满足什么条件时,
(1)抛物线与x轴有两个公共点?
(2)抛物线与x轴只有一个公共点?
(3)抛物线与x轴没有公共点?
二次方程ax2+bx+c=0中Δ>0
二次方程ax2+bx+c=0中Δ=0
二次方程ax2+bx+c=0中Δ<0
新课探究
情境导入
课堂小结
单击此处添加标题文本内容
抛物线y=ax2+bx+c
与x轴有公共点
二次方程ax2+bx+c=0
有实根
二次方程ax2+bx+c=0
的根的判别式Δ≥ 0
转化为
为化转
转化为
为化转
转化为
新课探究
情境导入
课堂小结
抛物线y=ax2+bx+c
与x轴无公共点
二次方程ax2+bx+c=0
无实根
二次方程ax2+bx+c=0
的根的判别式Δ<0
转化为
为化转
转化为
为化转
转化为
新课探究
情境导入
课堂小结
单击此处添加标题文本内容
课堂检测:
2、如果关于x的一元二次方程x2-2x+m=0有两个相等的实数根,则m= ,此时抛物线y=x2-2x+m与x轴有 个公共点.
1、二次方程x2+x-6=0的两根为x1=-3,x2=2,则二次函数y=x2+x-6的图象与x轴公共点的坐标为 .
(-3,0),(2,0)
1
1
新课探究
情境导入
课堂小结
课 堂 小 结
二次函数y=ax2+bx+c的图象与一元二次方程 ax2+bx+c=0的关系.
二次函数y=ax2+bx+c的图象
二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象与x轴公共点个数
二次方程ax2+bx+c=0的根的判别式
两个公共点
一个公共点
没有公共点
有两个不等实根
有两个相等实根
没有实根
=0
>0
<0
5.6 二次函数的图象与一元二次方程
