6.7 第2课时 概率的实际应用 课件(共15张PPT) 2024—2025年青岛版数学九年级下册
文档属性
| 名称 | 6.7 第2课时 概率的实际应用 课件(共15张PPT) 2024—2025年青岛版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 06:11:30 | ||
图片预览




文档简介
(共15张PPT)
第6章 事件的概率
6.7 利用画树状图和列表计算概率
第2课时 概率的实际应用
情 境 导 入
第2课时 概率的实际应用
1.等可能性事件的两个特征:
(1)出现的结果有限多个;
(2)各结果发生的可能性相等.
2.如何求等可能性事件的概率
树状图
列表法
单击此处添加标题文本内容
情境导入
新课探究
课堂小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.
用列表法和树状图法求概率有什么优点?
新 课 探 究
第2课时 概率的实际应用
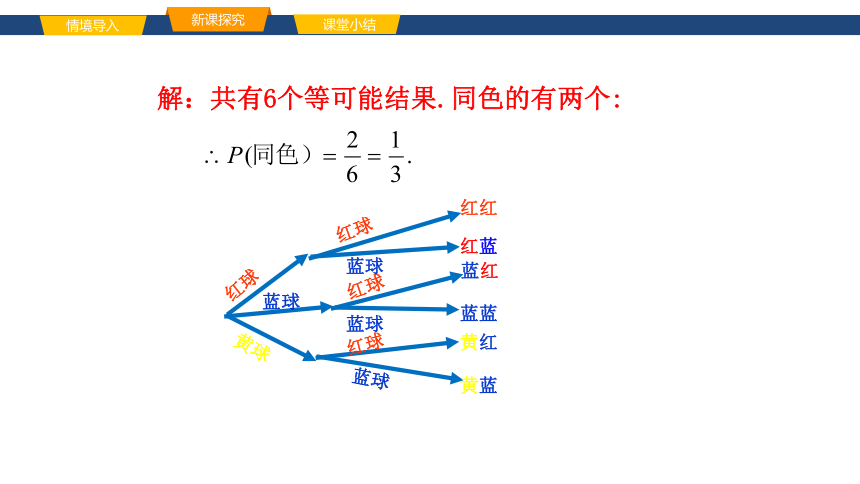
例1 甲乙两只不透明的袋子里装有除颜色之外都相同的球,甲袋装有红、蓝、黄色球各一个,乙袋装有红、蓝色球各一个,从每个袋子里分别随机地摸出一个球,两个球恰为同色的概率是多少?
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:共有6个等可能结果.同色的有两个:
红红
红球
红球
红球
红球
蓝球
蓝球
蓝球
蓝球
黄球
红蓝
蓝红
蓝蓝
黄红
黄蓝
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
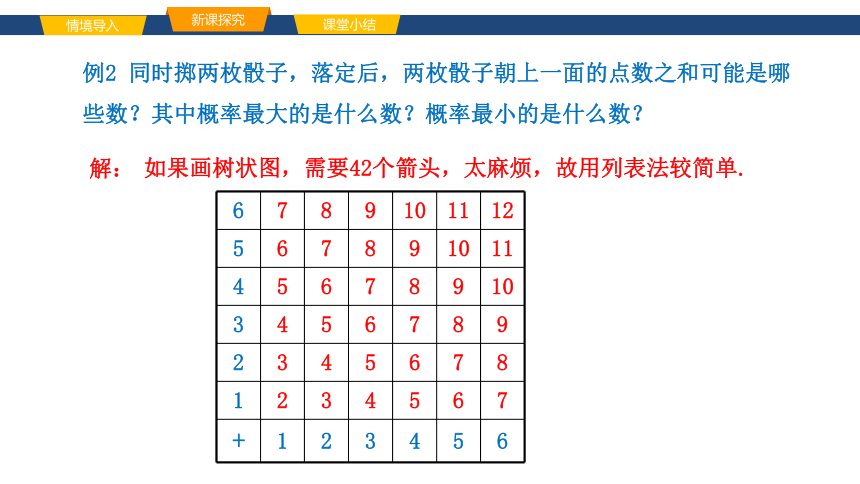
例2 同时掷两枚骰子,落定后,两枚骰子朝上一面的点数之和可能是哪些数?其中概率最大的是什么数?概率最小的是什么数?
解:
如果画树状图,需要42个箭头,太麻烦,故用列表法较简单.
6 7 8 9 10 11 12
5 6 7 8 9 10 11
4 5 6 7 8 9 10
3 4 5 6 7 8 9
2 3 4 5 6 7 8
1 2 3 4 5 6 7
+ 1 2 3 4 5 6
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
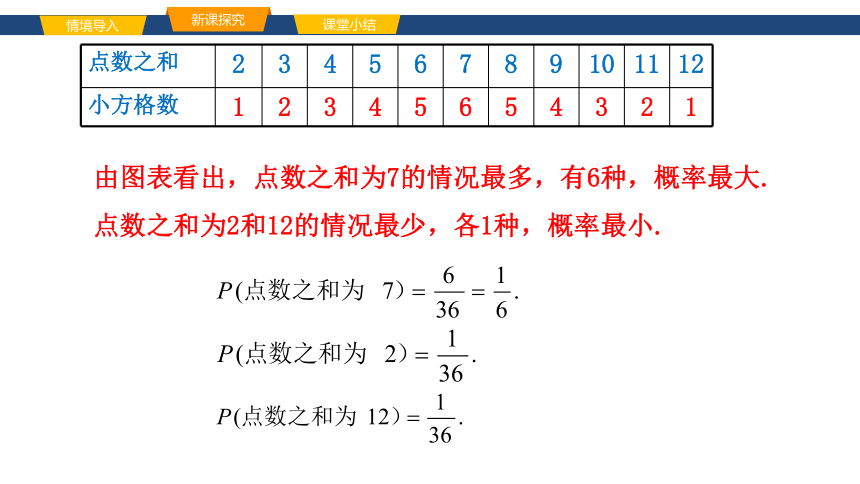
点数之和 2 3 4 5 6 7 8 9 10 11 12
小方格数 1 2 3 4 5 6 5 4 3 2 1
由图表看出,点数之和为7的情况最多,有6种,概率最大.点数之和为2和12的情况最少,各1种,概率最小.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用画树状图法方便.
归纳
新课探究
情境导入
课堂小结
挑战自我
下午放学后,小亮、小莹和大刚到学校乒乓球室去打乒乓球.当时只有一副空球桌,他们打算用“手心、手背“的方法决定哪两人先上场.游戏规则是:三人同时伸手心或手背,如果恰好其中有两人伸出的手势相同,那么这两人上场,否则重新开始.
假如这三个人每个人伸出手心或手背都是随机的,经过一次伸手实验,小亮上场的概率是多少?
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
手心
手背
小亮
小莹
手背
手心
手背
手心
手背
手心
手背
手心
手背
手心
手背
手心
解:根据题意,我们可以画出如下的树状图.
大刚
P(小亮出场)=
1.某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意拿一件衬衫和一条长裤,求正好是一套白色的概率_______.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
2.一个袋子中装有2个红球和2个绿球,任意摸出一球,记录颜色放回,再任意摸出一球,记录颜色放回,请你估计两次都摸到红球的概率是________.
9
1
4
1
课堂检测
3.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,当有三辆汽车经过这个十字路口时,求下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
左
右
直
第
一
辆
第
二
辆
第
三
辆
左直右
左
右
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种行驶方向
解:画树形图如下:
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
4.如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).
游戏规则是:如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
1
2
3
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:每次游戏时,所有可能出现的结果如下:
总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为.
转盘
摸球
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
(1,3)
(2,3)
课 堂 小 结
第2课时 概率的实际应用
本节课进一步学习利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用画树状图法方便.
第6章 事件的概率
6.7 利用画树状图和列表计算概率
第2课时 概率的实际应用
情 境 导 入
第2课时 概率的实际应用
1.等可能性事件的两个特征:
(1)出现的结果有限多个;
(2)各结果发生的可能性相等.
2.如何求等可能性事件的概率
树状图
列表法
单击此处添加标题文本内容
情境导入
新课探究
课堂小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.
用列表法和树状图法求概率有什么优点?
新 课 探 究
第2课时 概率的实际应用
例1 甲乙两只不透明的袋子里装有除颜色之外都相同的球,甲袋装有红、蓝、黄色球各一个,乙袋装有红、蓝色球各一个,从每个袋子里分别随机地摸出一个球,两个球恰为同色的概率是多少?
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:共有6个等可能结果.同色的有两个:
红红
红球
红球
红球
红球
蓝球
蓝球
蓝球
蓝球
黄球
红蓝
蓝红
蓝蓝
黄红
黄蓝
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例2 同时掷两枚骰子,落定后,两枚骰子朝上一面的点数之和可能是哪些数?其中概率最大的是什么数?概率最小的是什么数?
解:
如果画树状图,需要42个箭头,太麻烦,故用列表法较简单.
6 7 8 9 10 11 12
5 6 7 8 9 10 11
4 5 6 7 8 9 10
3 4 5 6 7 8 9
2 3 4 5 6 7 8
1 2 3 4 5 6 7
+ 1 2 3 4 5 6
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
点数之和 2 3 4 5 6 7 8 9 10 11 12
小方格数 1 2 3 4 5 6 5 4 3 2 1
由图表看出,点数之和为7的情况最多,有6种,概率最大.点数之和为2和12的情况最少,各1种,概率最小.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用画树状图法方便.
归纳
新课探究
情境导入
课堂小结
挑战自我
下午放学后,小亮、小莹和大刚到学校乒乓球室去打乒乓球.当时只有一副空球桌,他们打算用“手心、手背“的方法决定哪两人先上场.游戏规则是:三人同时伸手心或手背,如果恰好其中有两人伸出的手势相同,那么这两人上场,否则重新开始.
假如这三个人每个人伸出手心或手背都是随机的,经过一次伸手实验,小亮上场的概率是多少?
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
手心
手背
小亮
小莹
手背
手心
手背
手心
手背
手心
手背
手心
手背
手心
手背
手心
解:根据题意,我们可以画出如下的树状图.
大刚
P(小亮出场)=
1.某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意拿一件衬衫和一条长裤,求正好是一套白色的概率_______.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
2.一个袋子中装有2个红球和2个绿球,任意摸出一球,记录颜色放回,再任意摸出一球,记录颜色放回,请你估计两次都摸到红球的概率是________.
9
1
4
1
课堂检测
3.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,当有三辆汽车经过这个十字路口时,求下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
左
右
直
第
一
辆
第
二
辆
第
三
辆
左直右
左
右
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种行驶方向
解:画树形图如下:
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
4.如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).
游戏规则是:如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
1
2
3
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:每次游戏时,所有可能出现的结果如下:
总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为.
转盘
摸球
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
(1,3)
(2,3)
课 堂 小 结
第2课时 概率的实际应用
本节课进一步学习利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用画树状图法方便.
