7.4 第1课时 圆锥的有关概念及侧面积的计算 课件(共15张PPT) 2024—2025年青岛版数学九年级下册
文档属性
| 名称 | 7.4 第1课时 圆锥的有关概念及侧面积的计算 课件(共15张PPT) 2024—2025年青岛版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 06:12:29 | ||
图片预览



文档简介
(共15张PPT)
第7章 空间图形的
初步认识
7.4 圆锥的侧面展开图
第1课时 圆锥的有关概念及
侧面积的计算
情 境 导 入
第1课时 圆锥的有关概念及
侧面积的计算
圆的周长公式
圆的面积公式
C=2πr
S=πr2
弧长的计算公式
扇形面积计算公式
180
n R
l
p
=
2
360
n R
S
p
=
1
2
S lR
=
或
单击此处添加标题文本内容
情境导入
新课探究
课堂小结
新 课 探 究
第1课时 圆锥的有关概念及
侧面积的计算
圆锥的结构特征
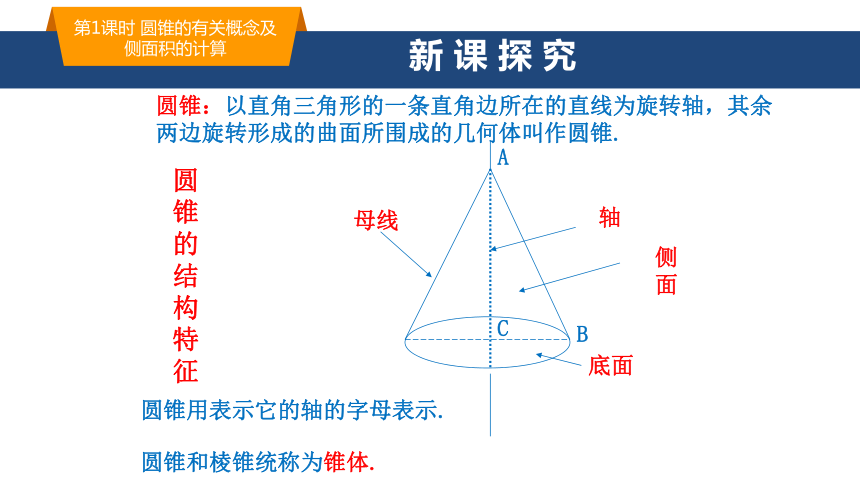
圆锥:以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫作圆锥.
轴
A
C
B
母线
侧面
底面
圆锥和棱锥统称为锥体.
圆锥用表示它的轴的字母表示.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
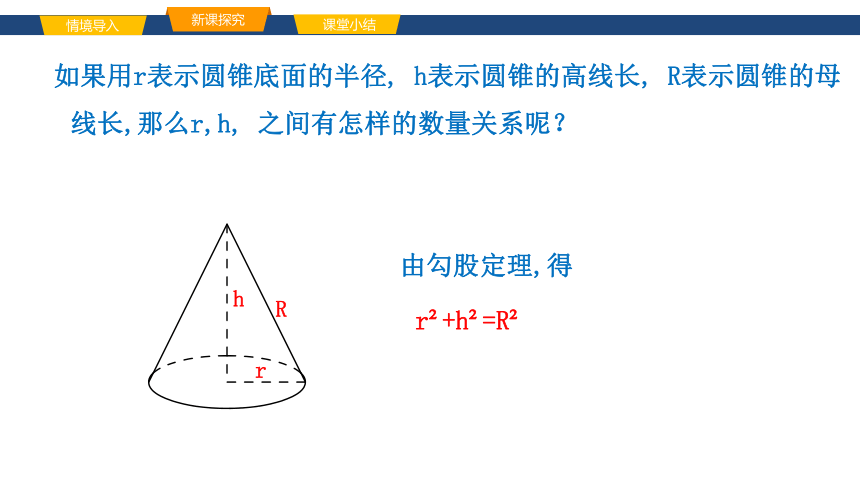
如果用r表示圆锥底面的半径, h表示圆锥的高线长, R表示圆锥的母线长,那么r,h, 之间有怎样的数量关系呢?
h
R
r
由勾股定理,得
r +h =R
新课探究
情境导入
课堂小结
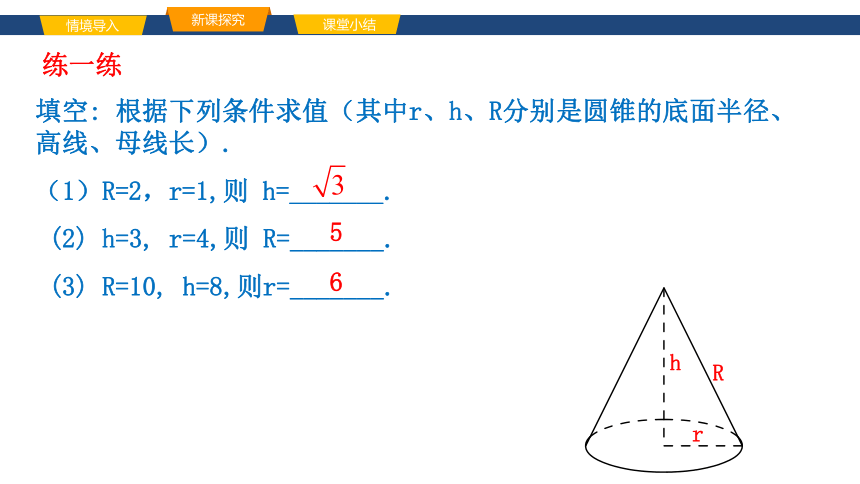
填空: 根据下列条件求值(其中r、h、R分别是圆锥的底面半径、高线、母线长).
(1)R=2,r=1,则 h=_______.
(2) h=3, r=4,则 R=_______.
(3) R=10, h=8,则r=_______.
5
6
h
R
r
练一练
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
展开
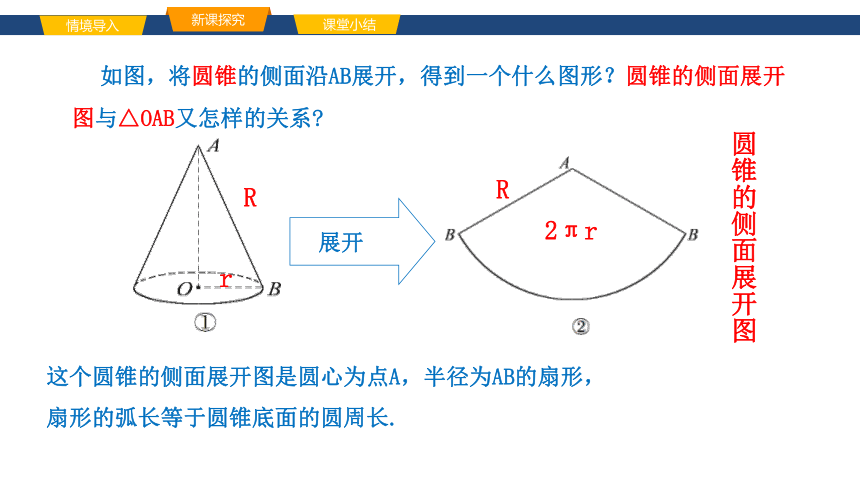
如图,将圆锥的侧面沿AB展开,得到一个什么图形?圆锥的侧面展开图与△OAB又怎样的关系
圆锥的侧面展开图
r
R
R
2πr
这个圆锥的侧面展开图是圆心为点A,半径为AB的扇形,
扇形的弧长等于圆锥底面的圆周长.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
圆锥的侧面积和全(表)面积
圆锥的底面周长就是其侧面展开图扇形的弧长,
圆锥的母线就是其侧面展开图扇形的半径.
即360r= nR
2
360
n R
s
p
=
侧
R
r
新课探究
情境导入
课堂小结
(2)已知一个圆锥的底面半径为12cm,母线长为20cm,则这个圆锥的侧面积为_________,全面积为___________.
(1)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为_______.
练一练
10cm
240πcm2
384πcm2
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例1 如图,已知圆锥形工件的地面直径是80cm、母线长50cm.
(1)求侧面展开图的圆心角,并画出侧面展开图:
(2)求圆锥的侧面积(精确到1cm2)
解:(1)由题意可知,圆锥的侧面展开图的扇形半径为 50cm,扇形弧长为80πcm.
∴扇形圆心角的度数n=(180×80π)÷50π=288(度).
(2)S侧=×50×80π≈6 283.
所以这个圆锥的侧面积为6 283cm2.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例2 如图,已知圆锥的底面直径为2、高为 2.求圆锥的母线长及表面积.
A
C
B
O
解:连接圆锥的顶点A与地面圆心O.
在Rt△AOB中,由题意可知
AO=2,OB=1.
由勾股定理,得
AB=
S侧=cl=×2π×3=3π.
S底=πr2=π×12=π.
∴S全=S侧+S全=3π+π=4π.
所以这个圆锥的母线长为3,表面积为4π.
1.一个圆锥的底面圆的周长是4π cm,母线长是6 cm,则该圆锥的侧面展开图的圆心角的度数是( )
(A)40° (B)80° (C)120° (D)150°
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
C
课堂检测
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
8 cm
4π
2.现有一个圆心角为90°,半径为8 cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为 cm.
2
3.根据下列条件求圆锥侧面积展开图的圆心θ角 (r、h、R
分别是圆锥的底面半径、高线、母线长)
(1)R = 2,r = 1 则θ=________.
(2)h=3, r=4 则θ=__________.
新课探究
情境导入
课堂小结
r
h
R
180°
288°
θ
课 堂 小 结
第1课时 圆锥的有关概念及
侧面积的计算
本节课我们认识了圆锥的侧面展开图,学会计算圆锥的侧面积和全面积,在认识圆锥的侧面积展开图时,应知道圆锥的底面周长就是其侧面展开图扇形的弧长.圆锥的母线就是其侧面展开图扇形的半径,这样在计算侧面积和全面积时才能做到熟练、准确.
第7章 空间图形的
初步认识
7.4 圆锥的侧面展开图
第1课时 圆锥的有关概念及
侧面积的计算
情 境 导 入
第1课时 圆锥的有关概念及
侧面积的计算
圆的周长公式
圆的面积公式
C=2πr
S=πr2
弧长的计算公式
扇形面积计算公式
180
n R
l
p
=
2
360
n R
S
p
=
1
2
S lR
=
或
单击此处添加标题文本内容
情境导入
新课探究
课堂小结
新 课 探 究
第1课时 圆锥的有关概念及
侧面积的计算
圆锥的结构特征
圆锥:以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫作圆锥.
轴
A
C
B
母线
侧面
底面
圆锥和棱锥统称为锥体.
圆锥用表示它的轴的字母表示.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
如果用r表示圆锥底面的半径, h表示圆锥的高线长, R表示圆锥的母线长,那么r,h, 之间有怎样的数量关系呢?
h
R
r
由勾股定理,得
r +h =R
新课探究
情境导入
课堂小结
填空: 根据下列条件求值(其中r、h、R分别是圆锥的底面半径、高线、母线长).
(1)R=2,r=1,则 h=_______.
(2) h=3, r=4,则 R=_______.
(3) R=10, h=8,则r=_______.
5
6
h
R
r
练一练
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
展开
如图,将圆锥的侧面沿AB展开,得到一个什么图形?圆锥的侧面展开图与△OAB又怎样的关系
圆锥的侧面展开图
r
R
R
2πr
这个圆锥的侧面展开图是圆心为点A,半径为AB的扇形,
扇形的弧长等于圆锥底面的圆周长.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
圆锥的侧面积和全(表)面积
圆锥的底面周长就是其侧面展开图扇形的弧长,
圆锥的母线就是其侧面展开图扇形的半径.
即360r= nR
2
360
n R
s
p
=
侧
R
r
新课探究
情境导入
课堂小结
(2)已知一个圆锥的底面半径为12cm,母线长为20cm,则这个圆锥的侧面积为_________,全面积为___________.
(1)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为_______.
练一练
10cm
240πcm2
384πcm2
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例1 如图,已知圆锥形工件的地面直径是80cm、母线长50cm.
(1)求侧面展开图的圆心角,并画出侧面展开图:
(2)求圆锥的侧面积(精确到1cm2)
解:(1)由题意可知,圆锥的侧面展开图的扇形半径为 50cm,扇形弧长为80πcm.
∴扇形圆心角的度数n=(180×80π)÷50π=288(度).
(2)S侧=×50×80π≈6 283.
所以这个圆锥的侧面积为6 283cm2.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例2 如图,已知圆锥的底面直径为2、高为 2.求圆锥的母线长及表面积.
A
C
B
O
解:连接圆锥的顶点A与地面圆心O.
在Rt△AOB中,由题意可知
AO=2,OB=1.
由勾股定理,得
AB=
S侧=cl=×2π×3=3π.
S底=πr2=π×12=π.
∴S全=S侧+S全=3π+π=4π.
所以这个圆锥的母线长为3,表面积为4π.
1.一个圆锥的底面圆的周长是4π cm,母线长是6 cm,则该圆锥的侧面展开图的圆心角的度数是( )
(A)40° (B)80° (C)120° (D)150°
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
C
课堂检测
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
8 cm
4π
2.现有一个圆心角为90°,半径为8 cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为 cm.
2
3.根据下列条件求圆锥侧面积展开图的圆心θ角 (r、h、R
分别是圆锥的底面半径、高线、母线长)
(1)R = 2,r = 1 则θ=________.
(2)h=3, r=4 则θ=__________.
新课探究
情境导入
课堂小结
r
h
R
180°
288°
θ
课 堂 小 结
第1课时 圆锥的有关概念及
侧面积的计算
本节课我们认识了圆锥的侧面展开图,学会计算圆锥的侧面积和全面积,在认识圆锥的侧面积展开图时,应知道圆锥的底面周长就是其侧面展开图扇形的弧长.圆锥的母线就是其侧面展开图扇形的半径,这样在计算侧面积和全面积时才能做到熟练、准确.
