8.3 第3课时 三视图的应用 课件(共15张PPT) 2024—2025年青岛版数学九年级下册
文档属性
| 名称 | 8.3 第3课时 三视图的应用 课件(共15张PPT) 2024—2025年青岛版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 06:12:54 | ||
图片预览





文档简介
(共15张PPT)
第8章 投影与识图
8.3 物体的三视图
第3课时 三视图的应用
情 境 导 入
第3课时 三视图的应用
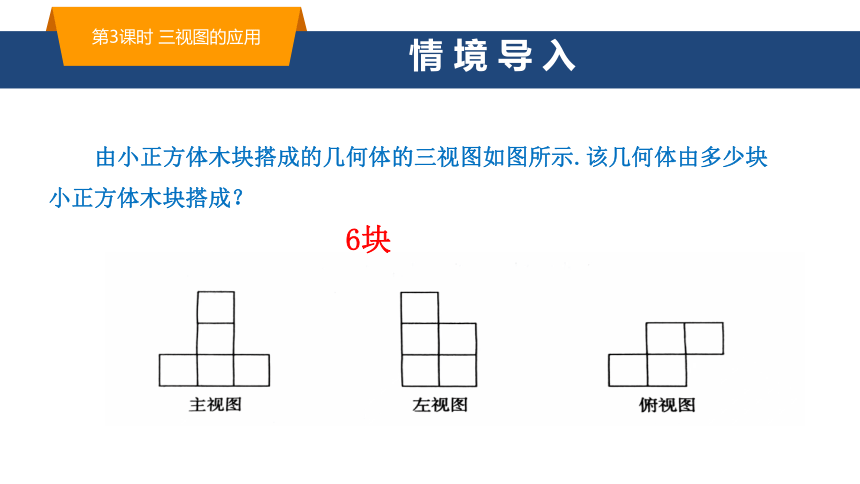
由小正方体木块搭成的几何体的三视图如图所示.该几何体由多少块小正方体木块搭成?
6块
新 课 探 究
第3课时 三视图的应用
例1 (1)一个几何体的三视图如图所示(单位:mm)根据三视图描述这个几何体的形状;
(2)画出这个几何体的表面展开图,并计算这个几何体的表面积(精确到1 mm );
(3)用硬纸板制作这个几何体的模型.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:(1)由主视图是等腰三角形,俯视图是半圆,左视图是直角三角形,并且左视图中直角三角形的底边等于俯视图中半圆的半径,还等于主视图中的等腰三角形底边的一半,可以想象这个几何体是由一个等腰三角形、一个半圆和半个圆锥面围成,等腰三角形的两腰是圆锥的母线,等腰三角形底边是底面半圆的直径,等腰三角形的高是圆锥的高.它是用圆锥的轴截面截得的半圆锥(如图),底面半圆的直径为300 mm,半圆锥的高为300 mm.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
(2)如图,在Rt△AOB中,由勾股定理
故这个几何体侧面展开图中扇形的半径AB约为335.4 mm.
扇形的圆心角为
根据以上数据,可画出这个几何体的表面展开图(如图).
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
几何体的表面积:
所以半圆锥的表面积
S=S扇形BAC′ + S半圆 + S△ABC.
≈79029.4+35342.9+45000≈159372(mm2).
因此,这个几何体的表面积约为159372 mm .
S扇形BAC′=
S半圆=
S△ABC=
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
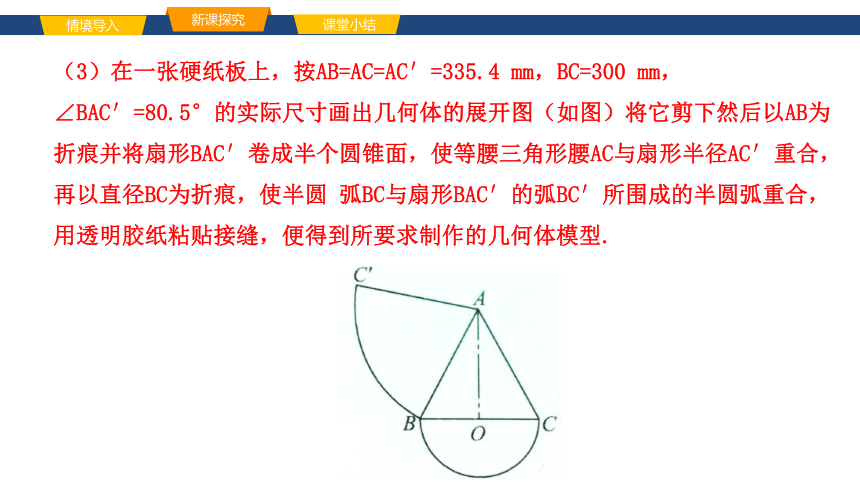
(3)在一张硬纸板上,按AB=AC=AC′=335.4 mm,BC=300 mm,∠BAC′=80.5°的实际尺寸画出几何体的展开图(如图)将它剪下然后以AB为折痕并将扇形BAC′卷成半个圆锥面,使等腰三角形腰AC与扇形半径AC′重合,再以直径BC为折痕,使半圆 弧BC与扇形BAC′的弧BC′所围成的半圆弧重合,用透明胶纸粘贴接缝,便得到所要求制作的几何体模型.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例2 用小正方体块搭成一个几何体,似的它的主视图和俯视图如图所示.这样的几何体只有一种吗?它最少需要多少个小正方体块?最多需要多少个小正方体块?请你画出这个几何体的所有可能的左视图.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:组成几何体可能8块、9块、10块或11块小正方体,最多需要11块,最少需要8块.因此主视图、俯视图所示的几何体有五种,其左视图分别为
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
1.已知一个几何体如图所示,画出它的主视图、俯视图和左视图.
课堂检测
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
2.一个几何体的三视图如图所示(单位:mm).
(1)根据三视图,画出这个几何体的表面展开图,并计算这个几何体的表面积;
(2)用硬纸板制作这个几何体的模型.
课堂检测
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
课堂检测
(2)如图所示.
解:(1)如图,表面积为200×200-2×2+(200+200+)×200
=(120000+40000)mm2.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
3.如图,是由一些大小相同的小正方体组成的几何体的我是图其中正方体中的数字表示该位置上的小正方体的个数,这个几何体的左视图( )
A
B
C
D
A
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
4.如图是由几个相同的小正方体叠成一个几何体,它的三视图如下。那么这个几何体是由( )小正方体组成
A 6块 B 5块 C 4块 D 3块
B
课 堂 小 结
第3课时 三视图的应用
三视图可以解决一些实际问题中的计算,同时也可以增强学生的空间观念,感悟平面图形与立体图形之间的相互转化.
几何体搭建这类问题,我们把前后称为行,左右称为列,上下称为层.由俯视图先确定行与列的分布,再由主视图确定每一列的最高层数.
第8章 投影与识图
8.3 物体的三视图
第3课时 三视图的应用
情 境 导 入
第3课时 三视图的应用
由小正方体木块搭成的几何体的三视图如图所示.该几何体由多少块小正方体木块搭成?
6块
新 课 探 究
第3课时 三视图的应用
例1 (1)一个几何体的三视图如图所示(单位:mm)根据三视图描述这个几何体的形状;
(2)画出这个几何体的表面展开图,并计算这个几何体的表面积(精确到1 mm );
(3)用硬纸板制作这个几何体的模型.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:(1)由主视图是等腰三角形,俯视图是半圆,左视图是直角三角形,并且左视图中直角三角形的底边等于俯视图中半圆的半径,还等于主视图中的等腰三角形底边的一半,可以想象这个几何体是由一个等腰三角形、一个半圆和半个圆锥面围成,等腰三角形的两腰是圆锥的母线,等腰三角形底边是底面半圆的直径,等腰三角形的高是圆锥的高.它是用圆锥的轴截面截得的半圆锥(如图),底面半圆的直径为300 mm,半圆锥的高为300 mm.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
(2)如图,在Rt△AOB中,由勾股定理
故这个几何体侧面展开图中扇形的半径AB约为335.4 mm.
扇形的圆心角为
根据以上数据,可画出这个几何体的表面展开图(如图).
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
几何体的表面积:
所以半圆锥的表面积
S=S扇形BAC′ + S半圆 + S△ABC.
≈79029.4+35342.9+45000≈159372(mm2).
因此,这个几何体的表面积约为159372 mm .
S扇形BAC′=
S半圆=
S△ABC=
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
(3)在一张硬纸板上,按AB=AC=AC′=335.4 mm,BC=300 mm,∠BAC′=80.5°的实际尺寸画出几何体的展开图(如图)将它剪下然后以AB为折痕并将扇形BAC′卷成半个圆锥面,使等腰三角形腰AC与扇形半径AC′重合,再以直径BC为折痕,使半圆 弧BC与扇形BAC′的弧BC′所围成的半圆弧重合,用透明胶纸粘贴接缝,便得到所要求制作的几何体模型.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例2 用小正方体块搭成一个几何体,似的它的主视图和俯视图如图所示.这样的几何体只有一种吗?它最少需要多少个小正方体块?最多需要多少个小正方体块?请你画出这个几何体的所有可能的左视图.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:组成几何体可能8块、9块、10块或11块小正方体,最多需要11块,最少需要8块.因此主视图、俯视图所示的几何体有五种,其左视图分别为
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
1.已知一个几何体如图所示,画出它的主视图、俯视图和左视图.
课堂检测
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
2.一个几何体的三视图如图所示(单位:mm).
(1)根据三视图,画出这个几何体的表面展开图,并计算这个几何体的表面积;
(2)用硬纸板制作这个几何体的模型.
课堂检测
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
课堂检测
(2)如图所示.
解:(1)如图,表面积为200×200-2×2+(200+200+)×200
=(120000+40000)mm2.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
3.如图,是由一些大小相同的小正方体组成的几何体的我是图其中正方体中的数字表示该位置上的小正方体的个数,这个几何体的左视图( )
A
B
C
D
A
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
4.如图是由几个相同的小正方体叠成一个几何体,它的三视图如下。那么这个几何体是由( )小正方体组成
A 6块 B 5块 C 4块 D 3块
B
课 堂 小 结
第3课时 三视图的应用
三视图可以解决一些实际问题中的计算,同时也可以增强学生的空间观念,感悟平面图形与立体图形之间的相互转化.
几何体搭建这类问题,我们把前后称为行,左右称为列,上下称为层.由俯视图先确定行与列的分布,再由主视图确定每一列的最高层数.
