4.3 探索三角形全等的条件(第二课时)课件 (共20张PPT) 2024-2025学年北师大版七年级数学下册
文档属性
| 名称 | 4.3 探索三角形全等的条件(第二课时)课件 (共20张PPT) 2024-2025学年北师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 06:18:03 | ||
图片预览


文档简介
(共20张PPT)
北师大版 数学七年级下册
第4章 三角形
4.3.2 探索三角形全等的条件
第2课时 ASA、AAS
1) 理解并区别“角边角”(ASA),
“角角边”(AAS)定理
2) 能运用定理判定两个三角形全等
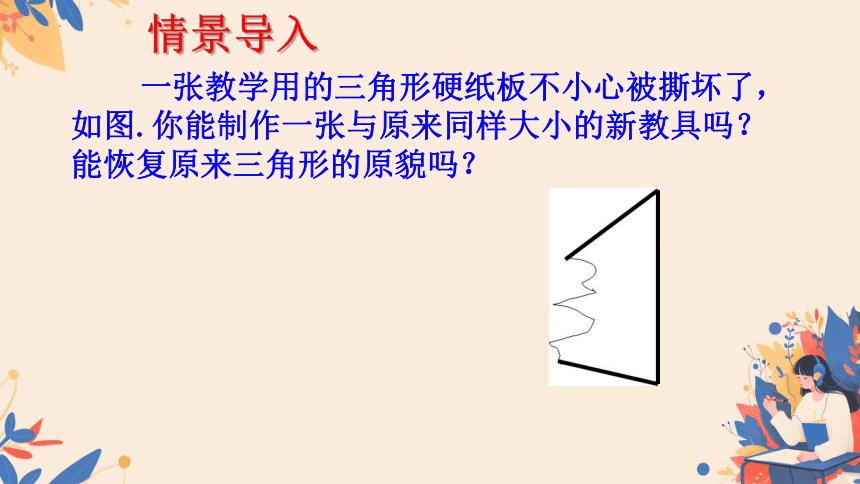
一张教学用的三角形硬纸板不小心被撕坏了,如图.你能制作一张与原来同样大小的新教具吗?能恢复原来三角形的原貌吗?
情景导入
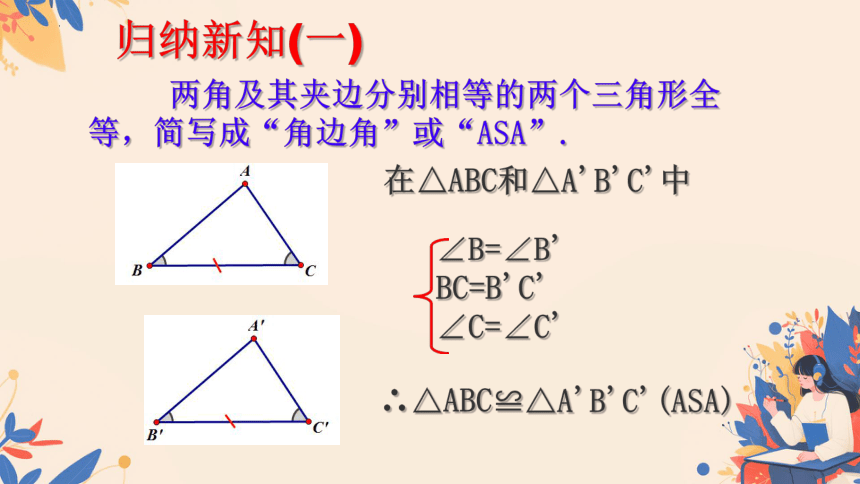
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
归纳新知(一)
在△ABC和△A'B'C'中
∠B=∠B' BC=B'C'
∠C=∠C'
∴△ABC≌△A'B'C'(ASA)
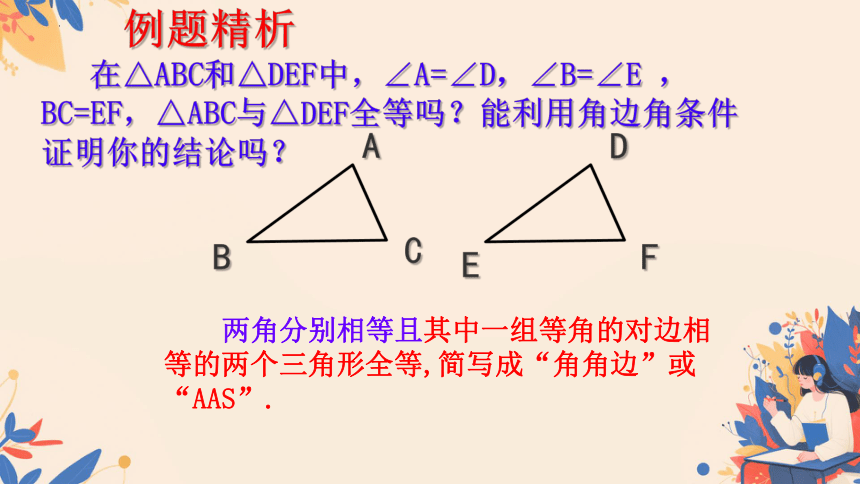
在△ABC和△DEF中,∠A=∠D,∠B=∠E ,
BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
例题精析
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
A
E
F
C
D
B
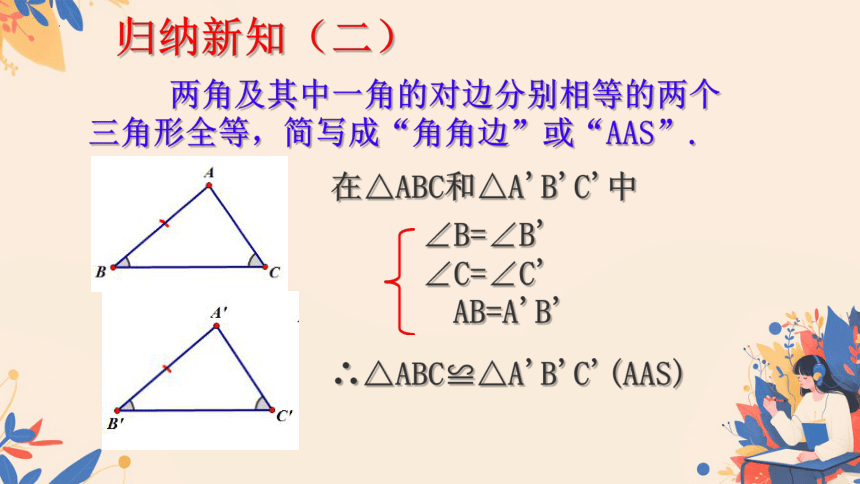
两角及其中一角的对边分别相等的两个三角形全等,简写成“角角边”或“AAS”.
归纳新知(二)
在△ABC和△A'B'C'中
∠B=∠B'
∠C=∠C'
AB=A'B'
∴△ABC≌△A'B'C'(AAS)
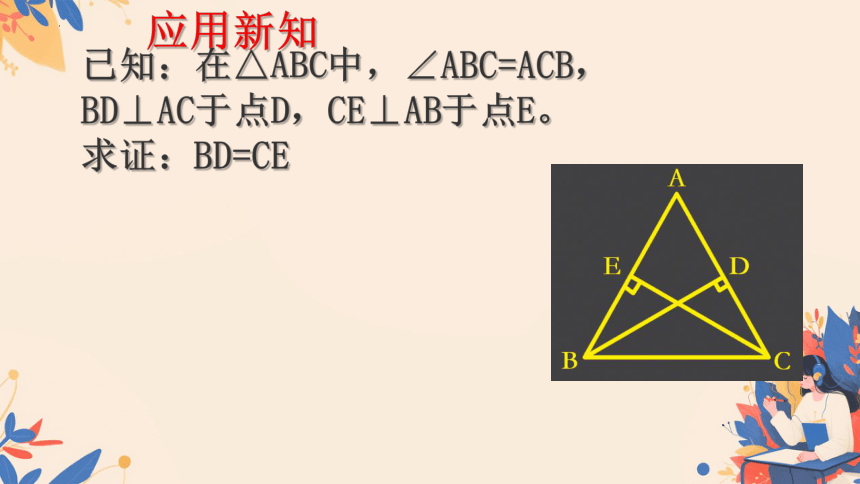
已知:在△ABC中,∠ABC=ACB,
BD⊥AC于点D,CE⊥AB于点E。
求证:BD=CE
应用新知
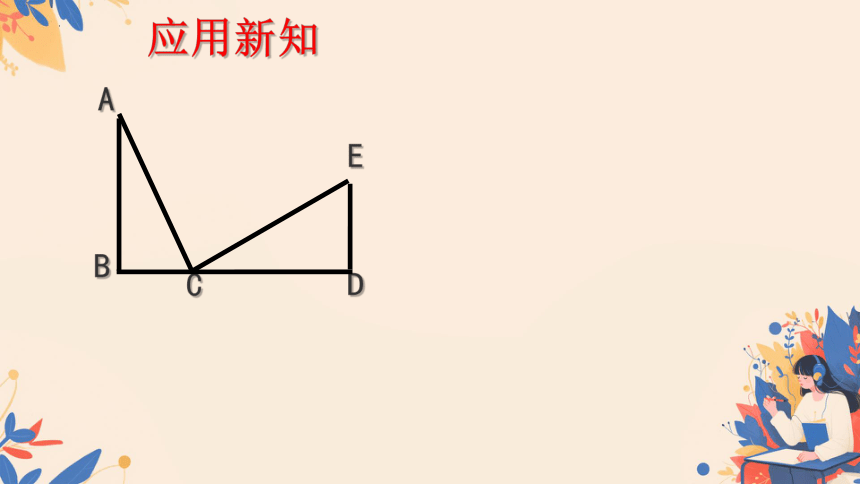
应用新知
A
D
C
B
E
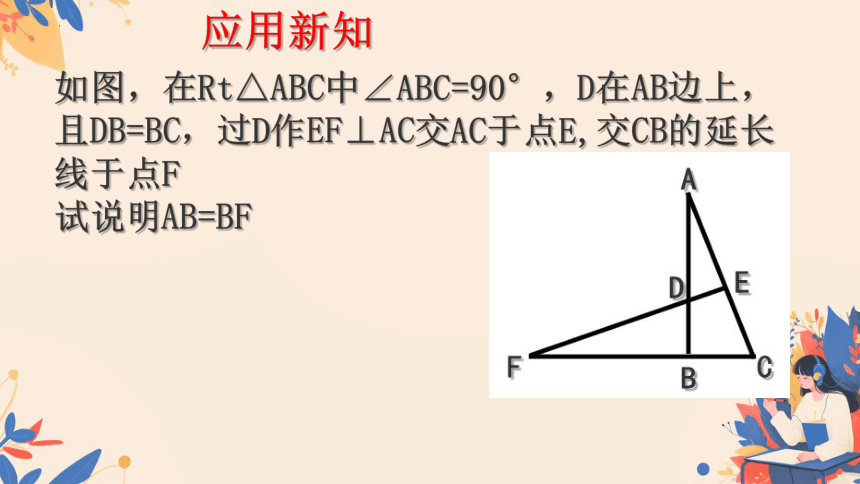
如图,在Rt△ABC中∠ABC=90°,D在AB边上,且DB=BC,过D作EF⊥AC交AC于点E,交CB的延长线于点F
试说明AB=BF
应用新知
应用新知
如图,AC平分∠DAB,∠D=∠B
说明:
已知:∠B=∠D,∠1=∠2,
说明:△ABC≌△ADC
例2.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长.为什么?
应用新知
【跟踪训练】
有几种填法
1.如图,应填什么就有 △AOC≌
△BOD
∠A=∠B(已知)
_______(已知)
∠C=∠D(已知)
所以△AOC≌△BOD( )
AC=BD
ASA
如图,应填什么就有△AOC≌△BOD
∠A=∠B (已知)
________ (已知)
∠C=∠D (已知)
所以△AOC≌△BOD( )
CO=DO
AAS
如图,应填什么就有△AOC≌△BOD
∠A=∠B(已知)
_______(已知)
∠C=∠D (已知)
所以△AOC≌△BOD( )
AO=BO
AAS
2.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长.为什么?
【解析】利用定理ASA判
定△ABC≌△EDC,
从而得DE=BA.
1.已知,如图,∠1=∠2,∠C=∠D,
求证:AC=AD.
【证明】
在△ABD和△ABC中
∠1=∠2 (已知)
所以△ABD≌△ABC (AAS)
∠D = ∠C (已知)
AB=AB(公共边)
所以AC=AD (全等三角形对应边相等)
2.如图,四边形ABCD是边长为2的正方形,点G是BC 延长线上一点,连接AG,点E,F分别在AG上, 连接BE,DF,∠1=∠2 , ∠3=∠4.
(1)证明:△ABE≌△DAF.
(2)若∠AGB=30°,求EF的长.
通过本课时的学习,需要我们掌握:
判定三角形全等的三种方法,它们分别是:
1.边边边(SSS)
2.角边角(ASA)
3.角角边(AAS)
“
”
THANKS
北师大版 数学七年级下册
第4章 三角形
4.3.2 探索三角形全等的条件
第2课时 ASA、AAS
1) 理解并区别“角边角”(ASA),
“角角边”(AAS)定理
2) 能运用定理判定两个三角形全等
一张教学用的三角形硬纸板不小心被撕坏了,如图.你能制作一张与原来同样大小的新教具吗?能恢复原来三角形的原貌吗?
情景导入
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
归纳新知(一)
在△ABC和△A'B'C'中
∠B=∠B' BC=B'C'
∠C=∠C'
∴△ABC≌△A'B'C'(ASA)
在△ABC和△DEF中,∠A=∠D,∠B=∠E ,
BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
例题精析
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
A
E
F
C
D
B
两角及其中一角的对边分别相等的两个三角形全等,简写成“角角边”或“AAS”.
归纳新知(二)
在△ABC和△A'B'C'中
∠B=∠B'
∠C=∠C'
AB=A'B'
∴△ABC≌△A'B'C'(AAS)
已知:在△ABC中,∠ABC=ACB,
BD⊥AC于点D,CE⊥AB于点E。
求证:BD=CE
应用新知
应用新知
A
D
C
B
E
如图,在Rt△ABC中∠ABC=90°,D在AB边上,且DB=BC,过D作EF⊥AC交AC于点E,交CB的延长线于点F
试说明AB=BF
应用新知
应用新知
如图,AC平分∠DAB,∠D=∠B
说明:
已知:∠B=∠D,∠1=∠2,
说明:△ABC≌△ADC
例2.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长.为什么?
应用新知
【跟踪训练】
有几种填法
1.如图,应填什么就有 △AOC≌
△BOD
∠A=∠B(已知)
_______(已知)
∠C=∠D(已知)
所以△AOC≌△BOD( )
AC=BD
ASA
如图,应填什么就有△AOC≌△BOD
∠A=∠B (已知)
________ (已知)
∠C=∠D (已知)
所以△AOC≌△BOD( )
CO=DO
AAS
如图,应填什么就有△AOC≌△BOD
∠A=∠B(已知)
_______(已知)
∠C=∠D (已知)
所以△AOC≌△BOD( )
AO=BO
AAS
2.如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长.为什么?
【解析】利用定理ASA判
定△ABC≌△EDC,
从而得DE=BA.
1.已知,如图,∠1=∠2,∠C=∠D,
求证:AC=AD.
【证明】
在△ABD和△ABC中
∠1=∠2 (已知)
所以△ABD≌△ABC (AAS)
∠D = ∠C (已知)
AB=AB(公共边)
所以AC=AD (全等三角形对应边相等)
2.如图,四边形ABCD是边长为2的正方形,点G是BC 延长线上一点,连接AG,点E,F分别在AG上, 连接BE,DF,∠1=∠2 , ∠3=∠4.
(1)证明:△ABE≌△DAF.
(2)若∠AGB=30°,求EF的长.
通过本课时的学习,需要我们掌握:
判定三角形全等的三种方法,它们分别是:
1.边边边(SSS)
2.角边角(ASA)
3.角角边(AAS)
“
”
THANKS
同课章节目录
