第五章专题复习:线段垂直平分线与角平分线的应用类型 课件(共29张PPT)
文档属性
| 名称 | 第五章专题复习:线段垂直平分线与角平分线的应用类型 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 09:22:55 | ||
图片预览

文档简介
(共29张PPT)
2025新七年级数学下册
第五章
——线段垂直平分线与角平分线
的应用类型专题复习
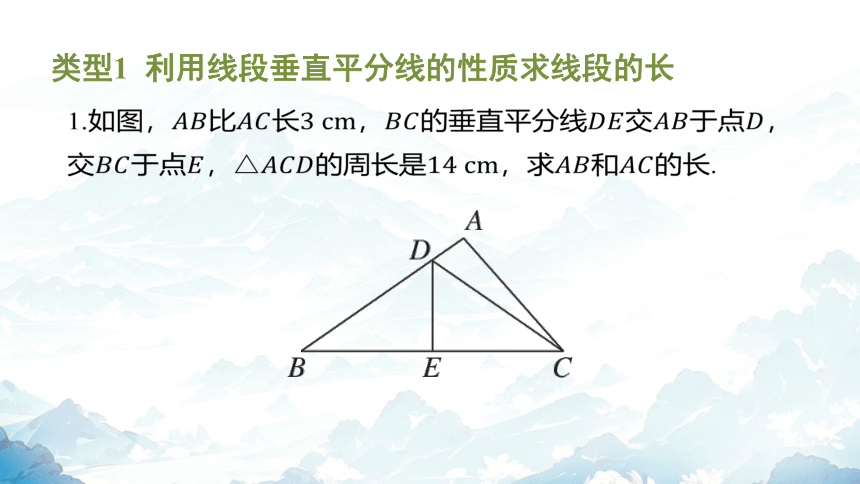
类型1 利用线段垂直平分线的性质求线段的长
1.如图,比长,的垂直平分线交于点 ,
交于点,的周长是,求和 的长.
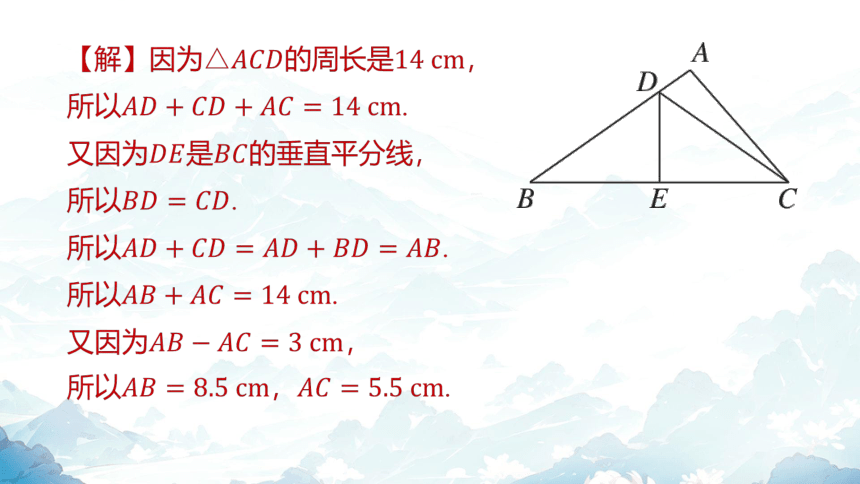
【解】因为的周长是 ,
所以 .
又因为是 的垂直平分线,
所以 .
所以 .
所以 .
又因为 ,
所以, .
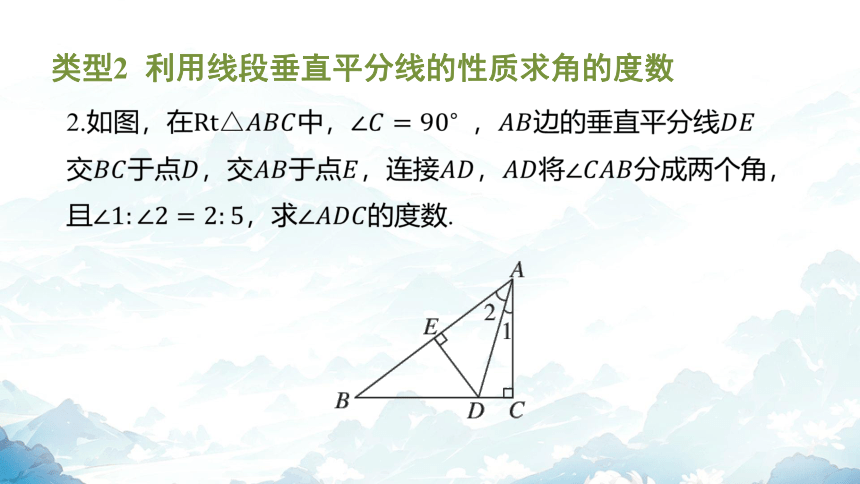
类型2 利用线段垂直平分线的性质求角的度数
2.如图,在中, ,边的垂直平分线
交于点,交于点,连接,将 分成两个角,
且,求 的度数.
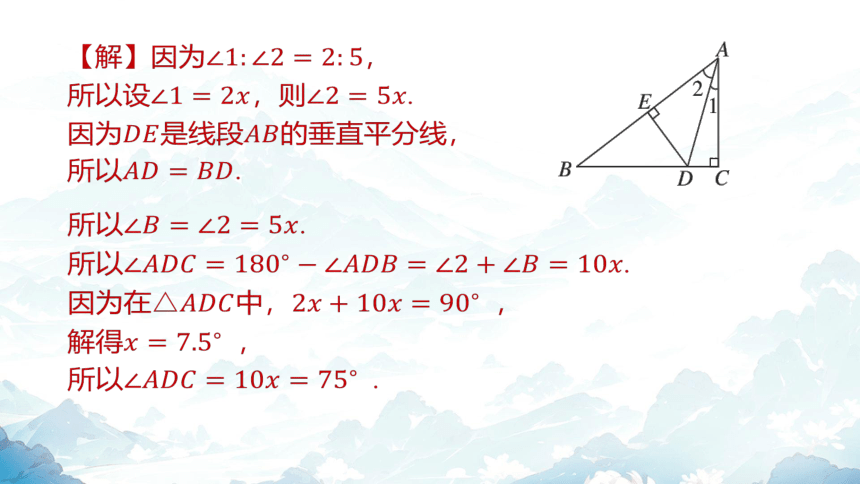
【解】因为 ,
所以设,则 .
因为是线段 的垂直平分线,
所以 .
所以 .
所以 .
因为在中, ,
解得 ,
所以 .
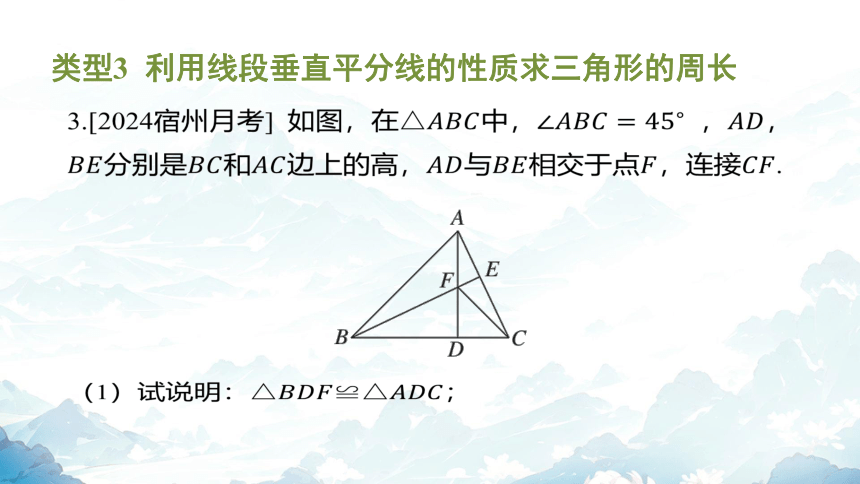
类型3 利用线段垂直平分线的性质求三角形的周长
3.[2024宿州月考] 如图,在中, , ,
分别是和边上的高,与相交于点,连接 .
(1)试说明: ;
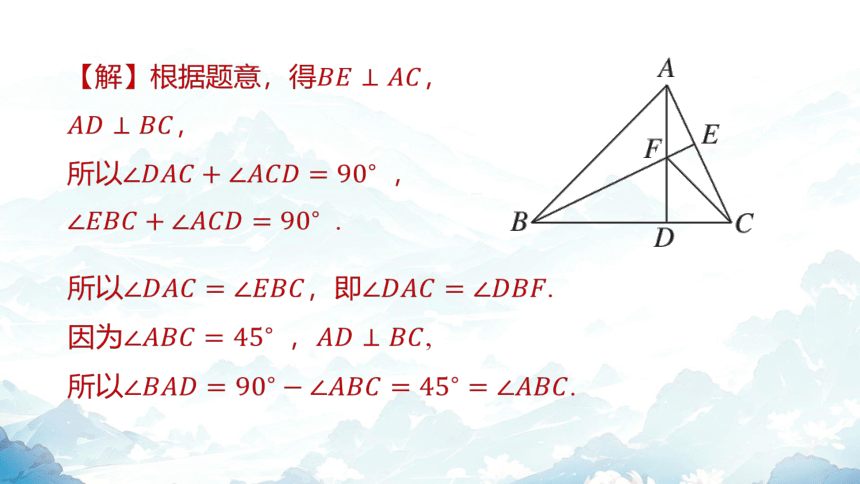
【解】根据题意,得 ,
,
所以 ,
.
所以,即 .
因为 , ,
所以 .
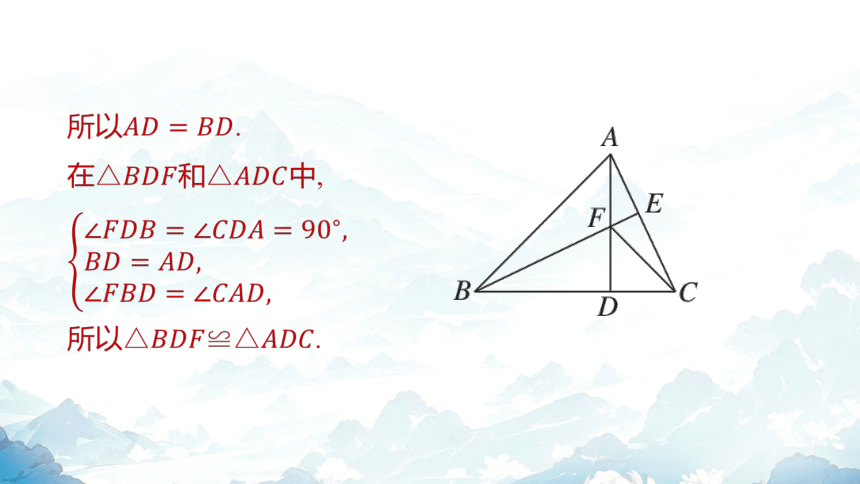
所以 .
在和 中,
所以 .
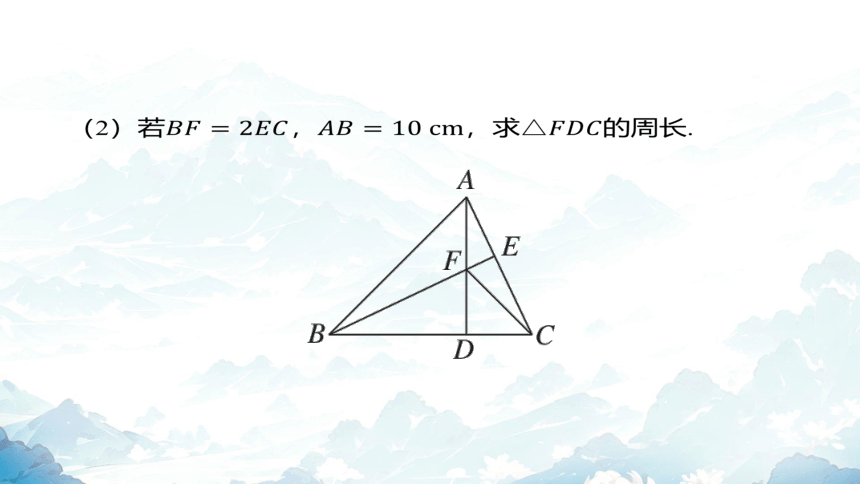
(2)若,,求 的周长.
【解】根据(1)得 ,
所以, .
又因为,所以 .
所以.因为 .
所以, .
所以 的周长
,
所以的周长为 .
类型4 利用线段垂直平分线、角平分线的性质解决实际
问题
4. 如图,某小区绿化带
内部有两个喷水管, ,现欲在
内部建一个水泵,使得水泵 到
,的距离相等,且到两个喷水管, 的距离也相等,
请你在图中标出水泵 的位置(保留作图痕迹).
【解】如图,以点 为圆心,任意长为
半径作弧交于,交于 ;分别以
,为圆心,大于 的长为半径作弧,
两弧交于;作射线;分别以, 为
圆心,大于的长为半径作弧,两弧交于点, ,连接
交于点, 即为水泵位置.
类型5 利用角平分线的性质解决面积问题
5. 如图, 的两条内角平分线相
交于点,过点作一条平分 面积
的直线,那么这条直线分成的两个图
形的周长比是( )
B
A. B. C. D.
【解析】
如图,连接,过点作于点,作于点 ,作
于点 ,
因为的两条内角平分线相交于点 ,
所以也是的角平分线,所以 .
过点作直线,设平分 的面积,则
.
因为, ,
,, ,
所以 .
所以 .
所以 .
所以 .
即这条直线分成的两个图形的周长比是 .
6.如图,在中,和的平分线相交于点 ,
过点作交于点,交于点,过点 作
于,,, .
(1)求 的周长;
【解】如图,因为与 的平
分线相交于点 ,
所以, .
因为 ,
所以, .
所以易得, .
所以 的周长为
,即 的周长为8.
(2)若,试求 的面积.
【解】如图,作于点 ,连接
,作于点 ,
因为和 的平分线相交于
点 ,
所以为 的三个内角平分线的交点.
所以平分 .
因为,, ,
所以 .
又因为 ,
所以 . 所以 .
所以 .
类型6 利用角平分线的性质说明线段的数量关系
7.已知是的平分线,点是射线上一点,点 ,
分别在射线,上,连接, .
(1)如图①,当,时,与 的数量关
系是_______________.
(2)如图②,点,在射线, 上滑动,且
,当时,与 在(1)中的数量关
系还成立吗?请说明理由.
【解】成立.理由:过点作于,
于,如图①,所以 .
又因为是 的平分线,
所以 .
因为,所以 .
又因为 ,
所以 .
又因为 ,
所以 .
在和中,
所以 .
所以 .
(3)如图③,如果 ,那么(1)中探
究的结论是否仍然成立?请说明理由.
【解】(1)中的结论仍然成立.
理由如下:如图②,过点作 于
,作于 ,
又因为平分,所以 .
因为 ,
,
所以 .
在和 中,
所以 ,
所以 .
2025新七年级数学下册
第五章
——线段垂直平分线与角平分线
的应用类型专题复习
类型1 利用线段垂直平分线的性质求线段的长
1.如图,比长,的垂直平分线交于点 ,
交于点,的周长是,求和 的长.
【解】因为的周长是 ,
所以 .
又因为是 的垂直平分线,
所以 .
所以 .
所以 .
又因为 ,
所以, .
类型2 利用线段垂直平分线的性质求角的度数
2.如图,在中, ,边的垂直平分线
交于点,交于点,连接,将 分成两个角,
且,求 的度数.
【解】因为 ,
所以设,则 .
因为是线段 的垂直平分线,
所以 .
所以 .
所以 .
因为在中, ,
解得 ,
所以 .
类型3 利用线段垂直平分线的性质求三角形的周长
3.[2024宿州月考] 如图,在中, , ,
分别是和边上的高,与相交于点,连接 .
(1)试说明: ;
【解】根据题意,得 ,
,
所以 ,
.
所以,即 .
因为 , ,
所以 .
所以 .
在和 中,
所以 .
(2)若,,求 的周长.
【解】根据(1)得 ,
所以, .
又因为,所以 .
所以.因为 .
所以, .
所以 的周长
,
所以的周长为 .
类型4 利用线段垂直平分线、角平分线的性质解决实际
问题
4. 如图,某小区绿化带
内部有两个喷水管, ,现欲在
内部建一个水泵,使得水泵 到
,的距离相等,且到两个喷水管, 的距离也相等,
请你在图中标出水泵 的位置(保留作图痕迹).
【解】如图,以点 为圆心,任意长为
半径作弧交于,交于 ;分别以
,为圆心,大于 的长为半径作弧,
两弧交于;作射线;分别以, 为
圆心,大于的长为半径作弧,两弧交于点, ,连接
交于点, 即为水泵位置.
类型5 利用角平分线的性质解决面积问题
5. 如图, 的两条内角平分线相
交于点,过点作一条平分 面积
的直线,那么这条直线分成的两个图
形的周长比是( )
B
A. B. C. D.
【解析】
如图,连接,过点作于点,作于点 ,作
于点 ,
因为的两条内角平分线相交于点 ,
所以也是的角平分线,所以 .
过点作直线,设平分 的面积,则
.
因为, ,
,, ,
所以 .
所以 .
所以 .
所以 .
即这条直线分成的两个图形的周长比是 .
6.如图,在中,和的平分线相交于点 ,
过点作交于点,交于点,过点 作
于,,, .
(1)求 的周长;
【解】如图,因为与 的平
分线相交于点 ,
所以, .
因为 ,
所以, .
所以易得, .
所以 的周长为
,即 的周长为8.
(2)若,试求 的面积.
【解】如图,作于点 ,连接
,作于点 ,
因为和 的平分线相交于
点 ,
所以为 的三个内角平分线的交点.
所以平分 .
因为,, ,
所以 .
又因为 ,
所以 . 所以 .
所以 .
类型6 利用角平分线的性质说明线段的数量关系
7.已知是的平分线,点是射线上一点,点 ,
分别在射线,上,连接, .
(1)如图①,当,时,与 的数量关
系是_______________.
(2)如图②,点,在射线, 上滑动,且
,当时,与 在(1)中的数量关
系还成立吗?请说明理由.
【解】成立.理由:过点作于,
于,如图①,所以 .
又因为是 的平分线,
所以 .
因为,所以 .
又因为 ,
所以 .
又因为 ,
所以 .
在和中,
所以 .
所以 .
(3)如图③,如果 ,那么(1)中探
究的结论是否仍然成立?请说明理由.
【解】(1)中的结论仍然成立.
理由如下:如图②,过点作 于
,作于 ,
又因为平分,所以 .
因为 ,
,
所以 .
在和 中,
所以 ,
所以 .
同课章节目录
