【中考押题卷】2025年广东省广州市中考数学模拟预测卷(含解析)
文档属性
| 名称 | 【中考押题卷】2025年广东省广州市中考数学模拟预测卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 00:00:00 | ||
图片预览




文档简介
2025年广州市中考数学模拟预测卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2025 广陵区一模)实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.|m|<|n| B.m+n>0 C.m﹣n<0 D.mn>0
2.(3分)(2025 浙江模拟)2025年2月12日,中国载人航天工程办公室宣布,载人月球探测任务的登月服命名为“望字”.已知月球距离地球的距离约为384000km,将384000用科学记数法表示为( )
A.3.84×105 B.384×103 C.3.84×103 D.0.384×106
3.(3分)(2024秋 遵义期中)将直角三角板(含30°)和直尺按如图方式摆放,则∠1的度数为( )
A.40° B.45° C.50° D.60°
4.(3分)(2022 华龙区校级模拟)下列各式计算正确的是( )
A.a2+2a3=a5 B.a a2=a3 C.a6÷a2=a3 D.(a2)3=a5
5.(3分)(2023秋 郑州期末)甲、乙两名战士在相同条件下各射击10次,每次命中的环数如下:甲:8,6,7,7,9,10,7,5,4,7;乙:7,9,8,5,6,7,7,6,7,8;以下选项正确的是( )
A.甲的平均数大于乙的平均数
B.甲的方差大于乙的方差
C.甲的中位数大于乙的中位数
D.甲的众数大于乙的众数
6.(3分)(2025 合肥二模)当x>0时,下列函数值y随x增大而增大的是( )
A.y=﹣5x+1 B. C.y=﹣x2 D.y=﹣x2+2x
7.(3分)(2024秋 洞口县期中)方程的根的情况是( )
A.没有实数根
B.两个相等的实数根
C.两个不相等的实数根
D.两个根分别为一个正根,一个负根
8.(3分)(2022 阿克苏地区一模)如图,O的直径AB=8,∠A=30°,点P在线段AB上,则PC的最小值为( )
A.2 B. C.4 D.
9.(3分)(2024 顺庆区二模)数学实践小组测量某路段上一处标识脱落的车辆限高杆MN的高度AB,如图,他们先用测角仪在C处测得点A的仰角∠AEG=30°,然后在D处测得点A的仰角∠AFG=45°,已知点C,D,B在同一条直线上,测角仪离地面高度CE=1m,CD=2m,则AB高( )
A.(2)m B.(1)m C.(3)m D.(2)m
10.(3分)护眼台灯亮度调节的原理是台灯内电路的电压为定值,通过控制可变电阻从而调节台灯的亮度,已知台灯的电流I(A)是电阻R(Ω)(R>0)的反比例函数,其函数图象如图所示,则下列说法正确的是( )
A.
B.该护眼台灯的电压为110V
C.若I≤5A,则R≥44Ω
D.当R=55Ω时,I=6A
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2025 东城区校级模拟)若二次根式有意义,则x的取值范围是 .
12.(3分)(2024 海淀区校级模拟)分式方程的解x= .
13.(3分)计算2025×5.052﹣2025×4.952的结果是 .
14.(3分)(2025 朝阳区一模)图①是小区围墙上的镂空花窗,其形状是扇形的一部分,图②是其示意图(阴影部分为镂空花窗).通过测量得到扇形AOB的圆心角为90°,OA=60cm,点C、D分别为OA、OB上靠近点O的三等分点,则这个镂空花窗的面积为 cm2(结果保留π).
15.(3分)(2024秋 苏州期末)对于一个函数,当自变量x取n时,其函数值y等于3n,我们称n为这个函数的“三倍数”.若二次函数y=x2+7x+2c有且只有一个“三倍数”,则c的值为 .
16.(3分)(2025 杭州一模)菱形ABCD绕点A旋转得到菱形AB'C'D',点B'在BC上,B'C'交CD于点E.若AB=2BB'=4,则CE的长为 .
三.解答题(共9小题,满分72分)
17.(4分)(2025 中宁县二模)解不等式组:.
18.(4分)(2022秋 道外区校级期中)化简求值:(2x+3y)2﹣(2x+y) (2x﹣y),其中x,y.
19.(6分)(2023秋 西城区校级期中)尺规作图,不写作法,保留作图痕迹.
(1)已知△ABC,现将△ABC绕点B逆时针旋转,使点A落在射线BP上,可得△A′C'B.
作法:
①在射线BP上截BA'=BA;
②以点B为圆心,BC长为半径作弧,以点A′为圆心,AC长为半径作弧,两弧在射线BP的右侧交于点C′;
③连接A'C',BC',则△A'C'B即为所求.
经过上述操作可知△A'C'B与△ACB的关系是 ,理由是 .
(2)如图,在直线MN上求作一点P,使点P到射线OA,OB的距离相等.
20.(6分)(2024 黄石开学)在浓度为15%的盐水中加入39千克水和1千克盐,浓度变为10%,这时,再加入多少千克盐,浓度变为20%?
21.(8分)(2025 禄丰市一模)“一寸光阴不可轻,最是书香能致远.”阅读是美好的,阅读是快乐的.某校社团将《西游记》中的四位人物的肖像制成编号为 A、B、C、D的四张卡片(除编号和人物肖像外其余完全相同),活动时学生根据所抽取的卡片来讲述他们在书中的故事.游戏规则如下:先将四张卡片背面朝上,洗匀放好,小东先从中随机抽取一张,记卡片上的人物为x,再把剩下的3张卡片洗匀后,背面向上放好,小华再从3张卡片中随机抽取一张,记卡片上的人物为y.若他们取出的两张卡片上对应的人物为师徒关系,则由小东讲,否则由小华讲.
(1)用列表法或画树状图法中的一种方法,列出(x,y)所有可能出现的结果;
(2)你认为这个游戏是否公平?请说明理由.
22.(10分)(2023 长安区一模)如图,在Rt△ABC中,∠BAC=90°,O为边BC上一点,以OB为半径的⊙O与AC相切于点D,连接BD.
(1)求证:BD平分∠ABC;
(2)连接AO,若∠AOB=90°,AB=4,求⊙O的半径.
23.(10分)(2024 广西三模)综合与实践
小涛在学习过程中发现:周长为定值的矩形中面积最大的是正方形.那么,面积为定值的矩形中,其周长的取值范围会如何呢?小涛尝试从函数的角度进行探究:
【建立模型】设一矩形的面积为4,周长为m,相邻的两边长分别为x,y,则,即,那么满足要求的(x,y)可以看作是函数与的图象在第 象限内的公共点坐标.
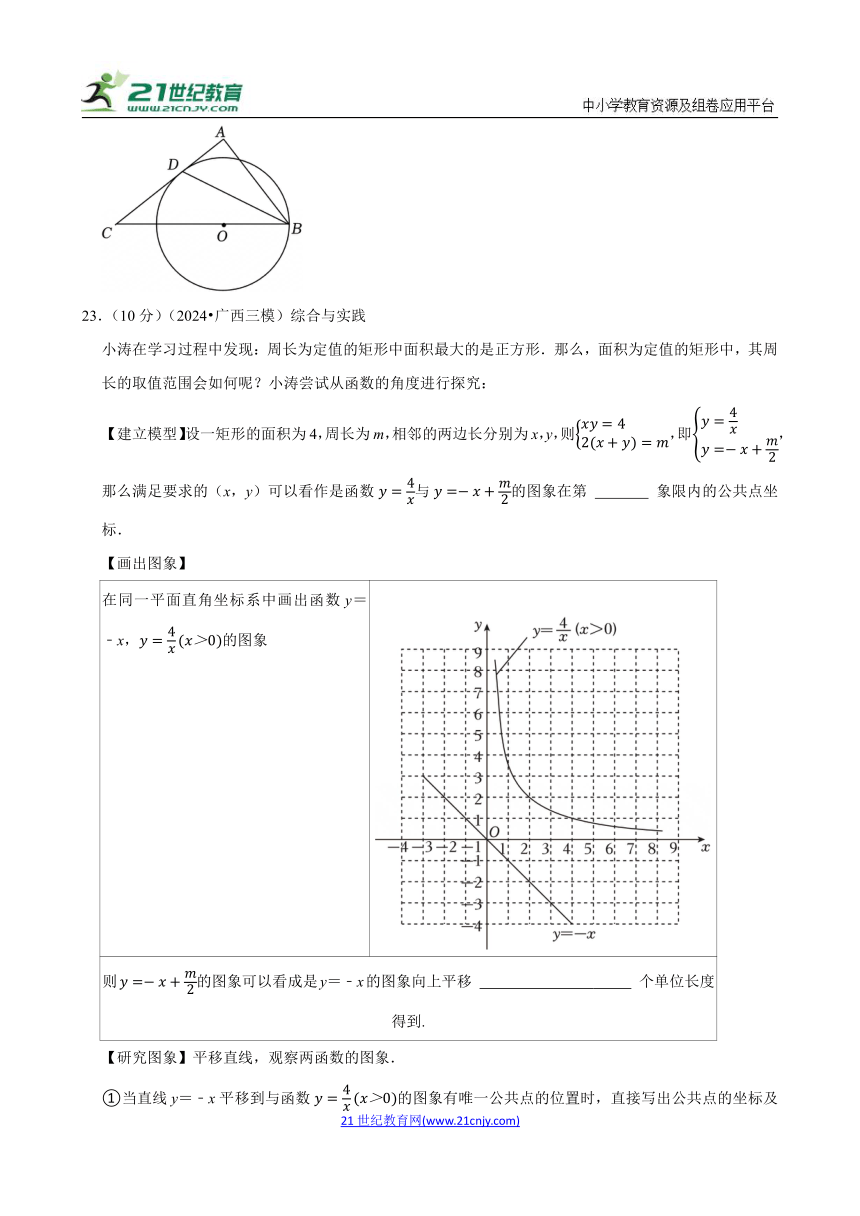
【画出图象】
在同一平面直角坐标系中画出函数y=﹣x,的图象
则的图象可以看成是y=﹣x的图象向上平移 个单位长度得到.
【研究图象】平移直线,观察两函数的图象.
①当直线y=﹣x平移到与函数的图象有唯一公共点的位置时,直接写出公共点的坐标及周长m的值.
②在直线平移的过程中,两函数图象公共点的个数还有什么情况?请直接写出公共点的个数及对应周长m的取值范围.
【结论运用】求面积为9的矩形的周长m的取值范围.
24.(12分)(2022 济源一模)已知抛物线y1=ax2﹣2ax+a+4(a≠0).
(1)求抛物线y1的顶点坐标;
(2)如图,当a=﹣1时,抛物线y1与x轴的负半轴、y轴分别交于点A、点B.
①将抛物线y1向右平移,使点A与原点重合.求平移后的抛物线y2的解析式;
②点P为抛物线y1上的一个动点,过点P作x轴的平行线l,若点P在由点B向顶点运动的过程中,直线l与抛物线y1、y2共有4个交点,请直接写出点P的纵坐标yp的取值范围.
25.(12分)(2022秋 汕尾期中)已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? (填“是”或“否”),∠BOE= 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
(2)如图c,在AB和AC上分别截取点B'和C',使AB'=AC',连接B′C′,将△AB'C'绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
2025年广州市中考数学模拟预测卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2025 广陵区一模)实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.|m|<|n| B.m+n>0 C.m﹣n<0 D.mn>0
【考点】实数与数轴;绝对值.
【专题】实数;运算能力.
【答案】B
【分析】根据实数m,n在数轴上的对应点的位置得到m和n的取值范围,逐个进行判断即可.
【解答】解:由题意得:﹣2<n<﹣1,3<m<4,m>n,
A、∵3<|m|<4,1<|n|<2,∴|m|>|n|,故A选项错误;
B、∵|m|>|n|,m+n>0,故B选项正确;
C、∵m>n,∴m﹣n>0,故C选项错误;
D、∵﹣2<n<﹣1,3<m<4,∴mn<0,故D选项错误.
故选:B.
【点评】本题考查了实数与数轴,绝对值,熟练掌握实数与数轴的对应关系是解题的关键.
2.(3分)(2025 浙江模拟)2025年2月12日,中国载人航天工程办公室宣布,载人月球探测任务的登月服命名为“望字”.已知月球距离地球的距离约为384000km,将384000用科学记数法表示为( )
A.3.84×105 B.384×103 C.3.84×103 D.0.384×106
【考点】科学记数法—表示较大的数.
【专题】实数;符号意识.
【答案】A.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:384000=3.84×105.
故选:A.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.(3分)(2024秋 遵义期中)将直角三角板(含30°)和直尺按如图方式摆放,则∠1的度数为( )
A.40° B.45° C.50° D.60°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】D
【分析】由两直线平行,内错角相等,即可得到答案.
【解答】解:∵AB∥CD,
∴∠1=∠2=60°.
故选:D.
【点评】本题考查平行线的性质,关键是掌握两直线平行,内错角相等.
4.(3分)(2022 华龙区校级模拟)下列各式计算正确的是( )
A.a2+2a3=a5 B.a a2=a3 C.a6÷a2=a3 D.(a2)3=a5
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】B
【分析】根据幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减;同底数幂相乘,底数不变指数相加,对各选项分析判断利用排除法求解.
【解答】解:A、a2与2a3不是同类项,不能合并,故本选项错误;
B、a a2=a1+2=a3,故本选项正确;
C、a6÷a2=a6﹣2=a4,故本选项错误;
D、(a2)3=a2×3=a6,故本选项错误.
故选:B.
【点评】本题考查了同底数幂的除法,同底数幂的乘法,幂的乘方的性质,熟记性质并理清指数的变化是解题的关键.
5.(3分)(2023秋 郑州期末)甲、乙两名战士在相同条件下各射击10次,每次命中的环数如下:甲:8,6,7,7,9,10,7,5,4,7;乙:7,9,8,5,6,7,7,6,7,8;以下选项正确的是( )
A.甲的平均数大于乙的平均数
B.甲的方差大于乙的方差
C.甲的中位数大于乙的中位数
D.甲的众数大于乙的众数
【考点】方差;算术平均数;中位数;众数.
【专题】统计的应用;应用意识.
【答案】B
【分析】本题考查平均数、方差、中位数和众数,解题的关键是掌握相关知识.分别求出甲、乙的平均数、方差、中位数、众数,即可求解.
【解答】解:A、∵7,7,
∴甲的平均数等于乙的平均数,A错误;
B、∵2.8,
2,
∴甲的方差大于乙的方差,B正确;
C、∵甲的中为数为:7,乙的中位数为:7,
∴甲的中位数等于乙的中位数,C错误;
D、∵甲的众数为7,乙的众数为7,
∴甲的众数等于乙的众数,D错误;
故选:B.
【点评】此题考查了平均数、中位数、众数和方差的意义,解题的关键是正确理解各概念的含义.
6.(3分)(2025 合肥二模)当x>0时,下列函数值y随x增大而增大的是( )
A.y=﹣5x+1 B. C.y=﹣x2 D.y=﹣x2+2x
【考点】反比例函数的性质;二次函数的性质;一次函数的性质.
【专题】一次函数及其应用;反比例函数及其应用;二次函数图象及其性质;推理能力.
【答案】B
【分析】分别根据一次函数的性质、反比例函数的性质、二次函数的性质逐项分析即可得出结论.
【解答】解:A、一次函数y=﹣5x+1的﹣5<0,函数值y随x增大而减小,不符合题意;
B、反比例函数的﹣5<0,当x>0时,函数值y随x增大而增大,正确,符合题意;
C、二次函数y=﹣x2的﹣1<0,开口向下,当x>0时,函数值y随x增大而减小,不符合题意;
D、二次函数y=﹣x2+2x的﹣1<0,开口向下,对称轴x=1,当x>1时,函数值y随x增大而减小,不符合题意.
故选:B.
【点评】本题考查了一次函数的性质、反比例函数的性质、二次函数的性质,熟知以上知识是解题的关键.
7.(3分)(2024秋 洞口县期中)方程的根的情况是( )
A.没有实数根
B.两个相等的实数根
C.两个不相等的实数根
D.两个根分别为一个正根,一个负根
【考点】根的判别式.
【专题】一元二次方程及应用;运算能力.
【答案】B
【分析】根据一元二次方程根的判别式即可解决问题.
【解答】解:由题知,
原方程可化为2x2x+3=0,
则0,
所以原方程有两个相等的实数根.
故选:B.
【点评】本题主要考查了根的判别式,熟知一元二次方程根的判别式是解题的关键.
8.(3分)(2022 阿克苏地区一模)如图,O的直径AB=8,∠A=30°,点P在线段AB上,则PC的最小值为( )
A.2 B. C.4 D.
【考点】圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】B
【分析】连接BC,由圆周角定理得出∠ACB=90°,由∠A=30°得出BC=4,求出AC=4,当CP⊥AB时,CP最小,CPAC=2得出答案.
【解答】解:连接BC,
∵AB是直径,
∴∠ACB=90°,
∵AB=8,∠A=30°,
∴BC=4,AC=4,
当CP⊥AB时,PC最小,
∵∠A=30°,
∴CPAC=2.
故选:B.
【点评】本题主要考查了圆周角定理,熟练掌握圆周角定理是解题的关键.
9.(3分)(2024 顺庆区二模)数学实践小组测量某路段上一处标识脱落的车辆限高杆MN的高度AB,如图,他们先用测角仪在C处测得点A的仰角∠AEG=30°,然后在D处测得点A的仰角∠AFG=45°,已知点C,D,B在同一条直线上,测角仪离地面高度CE=1m,CD=2m,则AB高( )
A.(2)m B.(1)m C.(3)m D.(2)m
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力;应用意识.
【答案】A
【分析】延长EF,交AB于点H,设HF=x米,在Rt△AHF中,可得AH=HF=x米,在Rt△AHE中,tan30°,求出x的值,进而可得出答案.
【解答】解:延长EF,交AB于点H,
由题意得,HB=DF=CE=1米,CD=FE=2米,
设HF=x米,
则EH=HF+FE=(x+2)米,
在Rt△AHF中,∠AFH=45°,
∴∠FAH=45°,
∴AH=HF=x米,
在Rt△AHE中,tan30°,
解得x1,
∴AB=AH+BH1+1(米).
故选:A.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
10.(3分)护眼台灯亮度调节的原理是台灯内电路的电压为定值,通过控制可变电阻从而调节台灯的亮度,已知台灯的电流I(A)是电阻R(Ω)(R>0)的反比例函数,其函数图象如图所示,则下列说法正确的是( )
A.
B.该护眼台灯的电压为110V
C.若I≤5A,则R≥44Ω
D.当R=55Ω时,I=6A
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】C
【分析】依据题意,先求出反比例函数的解析式,然后根据反比例函数性质逐项分析判断即可.
【解答】解:由题意,I,
∴U=2×110=220.
∴该反比例函数的解析式为I,故A错误.
∴该护眼台灯的电压为220V,故B错误.
若I≤5A,
∴5.
∴R≥44Ω,故C正确.
又当R=55Ω时,I=220÷55=4(A),
∴D错误.
故选:C.
【点评】本题主要考查了反比例函数的应用,解题时要熟练掌握并能灵活运用反比例函数的性质是关键.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2025 东城区校级模拟)若二次根式有意义,则x的取值范围是 x .
【考点】二次根式有意义的条件;解一元一次不等式.
【专题】二次根式;一元一次不等式(组)及应用;运算能力.
【答案】见试题解答内容
【分析】先根据二次根式有意义的条件得出5x﹣1≥0,再求出x的取值范围即可.
【解答】解:要使二次根式有意义,必须5x﹣1≥0,
解得:x,
所以x的取值范围是x.
故答案为:x.
【点评】本题考查了二次根式有意义的条件和解一元一次不等式,能根据二次根式有意义的条件得出5x﹣1≥0是解此题的关键.
12.(3分)(2024 海淀区校级模拟)分式方程的解x= .
【考点】解分式方程.
【专题】分式方程及应用;运算能力.
【答案】见试题解答内容
【分析】利用解分式方程的一般步骤解答即可.
【解答】解:去分母得:
2x=3﹣2×2(x﹣1),
去括号得:
2x=3﹣4x+4,
移项,合并同类项得:
6x=7,
∴x,
经检验,x是原方程的解,
∴x.
故答案为:.
【点评】本题主要考查了分式方程的解法,熟练掌握分式方程的解法的一般步骤是解题的关键.
13.(3分)计算2025×5.052﹣2025×4.952的结果是 2025 .
【考点】提公因式法与公式法的综合运用.
【专题】计算题;运算能力.
【答案】2025.
【分析】先提公因式法2025,再运用平方差公式计算即可.
【解答】解:原式=2025×(5.052﹣4.952)
=2025×(5.05+4.95)×(5.05﹣4.95)
=2025×10×0.1
=2025.
故答案为:1.
【点评】本题考查了提公因式法与公式法的综合运用,掌握因式分解的提公因式法、公式法是解决本题的关键.
14.(3分)(2025 朝阳区一模)图①是小区围墙上的镂空花窗,其形状是扇形的一部分,图②是其示意图(阴影部分为镂空花窗).通过测量得到扇形AOB的圆心角为90°,OA=60cm,点C、D分别为OA、OB上靠近点O的三等分点,则这个镂空花窗的面积为 (900π﹣200) cm2(结果保留π).
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(900π﹣200).
【分析】利用三角形和扇形的面积公式分别求出△COD和扇形AOB的面积,再根据“镂空花窗的面积=扇形AOB的面积﹣△COD的面积”计算即可.
【解答】解:∵OA=OB=60cm,点C、D分别为OA、OB上靠近点O的三等分点,
∴OC=OD60=20(cm),
∴SRt△COD OC OD 20×20=200(cm2),S扇形AOBπ×602=900π(cm2),
∴S阴影=S扇形AOB﹣SRt△COD =(900π﹣200)(cm2).
故答案为:(900π﹣200).
【点评】本题考查扇形面积的计算,掌握三角形和扇形面积计算公式是解题的关键.
15.(3分)(2024秋 苏州期末)对于一个函数,当自变量x取n时,其函数值y等于3n,我们称n为这个函数的“三倍数”.若二次函数y=x2+7x+2c有且只有一个“三倍数”,则c的值为 2 .
【考点】二次函数的性质.
【专题】新定义;二次函数图象及其性质;运算能力.
【答案】2.
【分析】先设二次函数y=x2+7x+2c的三倍点为(m,3m),然后即可得到方程m2+4m+2c=0,再根据二次函数y=x2+7x+2c有且只有一个“三倍数”,可知方程m2+4m+2c=0有两个相等的实数根,从而可以求得c的值.
【解答】解:设二次函数y=x2+7x+2c的三倍点为(m,3m),
则3m=m2+7m+2c,
∴m2+7m+2c﹣3m=0,
∴m2+4m+2c=0,
∵二次函数y=x2+7x+2c有且只有一个“三倍数”,
∴Δ=42﹣4×1×2c=0,
解得c=2,
故答案为:2.
【点评】本题考查二次函数的性质、新定义,解答本题的关键是明确题意,利用二次函数与方程的关系解答.
16.(3分)(2025 杭州一模)菱形ABCD绕点A旋转得到菱形AB'C'D',点B'在BC上,B'C'交CD于点E.若AB=2BB'=4,则CE的长为 .
【考点】旋转的性质;菱形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力;应用意识.
【答案】.
【分析】如图,过点C作CF∥C′D′,交B′C′于点F,根据等腰三角形的性质得到∠B=∠AB′B,根据平行线的性质得到∠B′CF=∠AB′B,根据相似三角形的性质得到FC,由旋转可知DD′=BB′=2求得C′D=2,又由CF∥C′D,根据相似三角形的性质即可得到结论.
【解答】解:如图,过点C作CF∥C′D′,交B′C′于点F,
∵菱形AB′C′D′中,AB′∥C′D′,
∴AB′∥CF∥C′D′,
∵AB=AB′,
∴∠B=∠AB′B,
∵∠AB′C′=∠B,
∴∠FB′C=∠BAB′,
∵AB′∥FC,
∴∠B′CF=∠AB′B,
∵AB=2BB'=4,
∴B′C=BB′=2,
∴△ABB′∽△B′CF,
∴,
∴,
∴FC=1,
由旋转可知,△ABB′≌△ADD′,
∴DD′=BB′=2,
∴C′D=2,
又由CF∥C′D,
∴△C′DE∽△FCE,
∴,
∴,
∴,
∴CE.
故答案为:.
【点评】本题主要考查旋转的性质,菱形的性质,等腰三角形三线合一,相似三角形的性质与判定,解直角三角形的应用等,正确地作出辅助线是解题关键.
三.解答题(共9小题,满分72分)
17.(4分)(2025 中宁县二模)解不等式组:.
【考点】解一元一次不等式组.
【专题】一元一次不等式(组)及应用;运算能力.
【答案】.
【分析】根据解一元一次不等式组的步骤,对所给不等式组进行求解即可.
【解答】解:,
解不等式①得,x≤3;
解不等式②得,x,
所以不等式组的解集为:.
【点评】本题主要考查了解一元一次不等式组,熟知解一元一次不等式组的步骤是解题的关键.
18.(4分)(2022秋 道外区校级期中)化简求值:(2x+3y)2﹣(2x+y) (2x﹣y),其中x,y.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】12xy+10y2,.
【分析】先用平方差公式和完全平方公式展开,再去括号,合并同类项,化简后将x,y的值代入计算即可.
【解答】解:原式=4x2+12xy+9y2﹣(4x2﹣y2)
=4x2+12xy+9y2﹣4x2+y2
=12xy+10y2,
当x,y时,
原式=12()+10×()2
=﹣2+10
=﹣2
.
【点评】本题考查整式化简求值,解题的关键是掌握平方差公式和完全平方公式,把所求式子化简.
19.(6分)(2023秋 西城区校级期中)尺规作图,不写作法,保留作图痕迹.
(1)已知△ABC,现将△ABC绕点B逆时针旋转,使点A落在射线BP上,可得△A′C'B.
作法:
①在射线BP上截BA'=BA;
②以点B为圆心,BC长为半径作弧,以点A′为圆心,AC长为半径作弧,两弧在射线BP的右侧交于点C′;
③连接A'C',BC',则△A'C'B即为所求.
经过上述操作可知△A'C'B与△ACB的关系是 △A'C'B≌△ACB ,理由是 SSS .
(2)如图,在直线MN上求作一点P,使点P到射线OA,OB的距离相等.
【考点】作图﹣旋转变换;角平分线的性质;作图—基本作图.
【专题】图形的全等;平移、旋转与对称;几何直观.
【答案】(1)△A'C'B≌△ACB;SSS.
(2)见解答.
【分析】(1)根据全等三角形的判定可得答案.
(2)作∠AOB的平分线,交MN于点P,则点P即为所求.
【解答】解:(1)由作图可得,BC=BC',AC=A'C',
∵BA'=BA,
∴△A'C'B≌△ACB(SSS).
故答案为:△A'C'B≌△ACB;SSS.
(2)如图2,点P即为所求.
【点评】本题考查作图﹣基本作图、角平分线的性质、全等三角形的判定,熟练掌握角平分线的性质、全等三角形的判定是解答本题的关键.
20.(6分)(2024 黄石开学)在浓度为15%的盐水中加入39千克水和1千克盐,浓度变为10%,这时,再加入多少千克盐,浓度变为20%?
【考点】一元一次方程的应用;百分数的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】再加入12.5千克盐,浓度变为20%.
【分析】先设原来有15%的盐水x千克,根据“浓度变为10%”列方程求出x的值,再依据新浓度列出算式计算即可.
【解答】解:设原来有15%的盐水x千克,
由题意,得(15% x+1)÷(x+39+1)=10%,
解得:x=60,
(60+39+1)(1﹣10% )÷(1﹣20% )﹣(60+39+1)
=100×(1﹣0.1)÷(1﹣0.2)﹣100
=90÷0.8﹣100
=112.5﹣100
=12.5(千克),
答:再加入12.5千克盐,浓度变为20%.
【点评】本题考查百分数的应用,一元一次方程的应用,解题的关键是读懂题意,列出方程,掌握解一元一次方程的方法是解题的关键.
21.(8分)(2025 禄丰市一模)“一寸光阴不可轻,最是书香能致远.”阅读是美好的,阅读是快乐的.某校社团将《西游记》中的四位人物的肖像制成编号为 A、B、C、D的四张卡片(除编号和人物肖像外其余完全相同),活动时学生根据所抽取的卡片来讲述他们在书中的故事.游戏规则如下:先将四张卡片背面朝上,洗匀放好,小东先从中随机抽取一张,记卡片上的人物为x,再把剩下的3张卡片洗匀后,背面向上放好,小华再从3张卡片中随机抽取一张,记卡片上的人物为y.若他们取出的两张卡片上对应的人物为师徒关系,则由小东讲,否则由小华讲.
(1)用列表法或画树状图法中的一种方法,列出(x,y)所有可能出现的结果;
(2)你认为这个游戏是否公平?请说明理由.
【考点】游戏公平性;列表法与树状图法.
【专题】概率及其应用;数据分析观念.
【答案】(1)见解答;
(2)游戏规则公平,理由见解答.
【分析】(1)列表可得所有等可能结果;
(2)从表格中得出取出的两张卡片上对应的人物为师徒关系的结果数,继而求出小东、小华讲的概率,从而得出答案.
【解答】解:(1)列表如下:
A B C D
A (B,A) (C,A) (D,A)
B (A,B) (C,B) (D,B)
C (A,C) (B,C) (D,C)
D (A,D) (B,D) (C,D)
共有12种等可能的结果;
(2)游戏规则公平,理由如下:
由表知,他们取出的两张卡片上对应的人物为师徒关系的结果有6种,
∴由小东讲的概率为,
则由小华讲的概率为1,
∵,
∴此游戏规则公平.
【点评】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
22.(10分)(2023 长安区一模)如图,在Rt△ABC中,∠BAC=90°,O为边BC上一点,以OB为半径的⊙O与AC相切于点D,连接BD.
(1)求证:BD平分∠ABC;
(2)连接AO,若∠AOB=90°,AB=4,求⊙O的半径.
【考点】相似三角形的判定与性质;垂径定理;圆周角定理;切线的性质.
【专题】等腰三角形与直角三角形;与圆有关的位置关系;图形的相似;运算能力;推理能力.
【答案】(1)证明见解答;
(2)⊙O的半径为22.
【分析】(1)连接OD,则OD=OB,得∠ODB=∠CBD,由切线的性质得∠ODC=∠BAC=90°,则DO∥AB,所以∠ODB=∠ABD,则∠CBD=∠ABD,所以BD平分∠ABC;
(2)设OB=DO=r,由OD∥AB,得△DOC∽△ABC,则,所以DO CB=AB CO,再证明△COD≌△ABO,得CO=AB=4,于是得r(4+r)=4×4,解方程求出符合题意的r的值即可.
【解答】(1)证明:连接OD,则OD=OB,
∴∠ODB=∠CBD,
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ODC=∠BAC=90°,
∴DO∥AB,
∴∠ODB=∠ABD,
∴∠CBD=∠ABD,
∴BD平分∠ABC.
(2)解:设OB=DO=r,
∵OD∥AB,
∴△DOC∽△ABC,
∴,
∴DO CB=AB CO,
∵∠COD=∠ABO,DO=OB,∠ODC=∠BAC=90°,
∴△COD≌△ABO(ASA),
∴CO=AB=4,
∴r(4+r)=4×4,
解得r1=22,r2=﹣22(不符合题意,舍去),
∴⊙O的半径为22.
【点评】此题重点考查等腰三角形的性质、平行线的判定与性质、角平分线的定义、切线的性质、相似三角形的判定与性质等知识,正确地作出所需要的辅助线是解题的关键.
23.(10分)(2024 广西三模)综合与实践
小涛在学习过程中发现:周长为定值的矩形中面积最大的是正方形.那么,面积为定值的矩形中,其周长的取值范围会如何呢?小涛尝试从函数的角度进行探究:
【建立模型】设一矩形的面积为4,周长为m,相邻的两边长分别为x,y,则,即,那么满足要求的(x,y)可以看作是函数与的图象在第 一 象限内的公共点坐标.
【画出图象】
在同一平面直角坐标系中画出函数y=﹣x,的图象
则的图象可以看成是y=﹣x的图象向上平移 个单位长度得到.
【研究图象】平移直线,观察两函数的图象.
①当直线y=﹣x平移到与函数的图象有唯一公共点的位置时,直接写出公共点的坐标及周长m的值.
②在直线平移的过程中,两函数图象公共点的个数还有什么情况?请直接写出公共点的个数及对应周长m的取值范围.
【结论运用】求面积为9的矩形的周长m的取值范围.
【考点】反比例函数综合题.
【专题】代数综合题;运算能力;推理能力.
【答案】【建立模型】一;
【画出图象】;
【研究图象】①(2,2),8;
②0个交点时,0<m<8;2个交点时,m>8;1个交点时,m=8;
【结论运用】m≥12.
【分析】【建立模型】由x>0,y>0,可得(x,y)在第一象限;
【画出图象】求出y=﹣x与x轴的交点坐标,即可求解;
【研究图象】①联立方程组,可求解;②在直线平移过程中,交点个数有:0个、1个、2个三种情况,结合图象可求解;
【结论运用】联立方程组,可得2x2﹣mx+18=0,由根的判别式可求解.
【解答】解:【建立模型】x,y都是边长,因此,都是正数,
故点(x,y)在第一象限,
故答案为:一;
【画出图象】∵y=﹣x与x轴的交点为(,0),
∴y=﹣x+的图象可以看成是由y=﹣x的图象向右平移个单位长度得到,
故答案为:;
【研究图象】①联立方程组可得,
整理得:x2mx+4=0,
∵两图象有唯一交点,
∴Δm2﹣16=0,
∴m=8,
∴x28x+4=0,
解得:x=2,
∴交点坐标为(2,2),
故答案为:(2,2),8;
②由①知:0个交点时,0<m<8;2个交点时,m>8;1个交点时,m=8;
【结论运用】设相邻的两边长为x、y,则x y=9,2(x+y)=m,即y,y=﹣x,
联立方程组可得,
整理得:2x2﹣mx+18=0,
∵两函数有交点,
∴Δ=m2﹣4×2×18≥0,
解得m≥12或m≤﹣12(不符合题意,舍去),
∴m≥12.
【点评】本题属于反比例函数综合题,考查了反比例函数的性质,一次函数的性质,矩形的性质等知识,解题的关键是理解题意,学会利用数形结合的思想解决问题,属于中考压轴题.
24.(12分)(2022 济源一模)已知抛物线y1=ax2﹣2ax+a+4(a≠0).
(1)求抛物线y1的顶点坐标;
(2)如图,当a=﹣1时,抛物线y1与x轴的负半轴、y轴分别交于点A、点B.
①将抛物线y1向右平移,使点A与原点重合.求平移后的抛物线y2的解析式;
②点P为抛物线y1上的一个动点,过点P作x轴的平行线l,若点P在由点B向顶点运动的过程中,直线l与抛物线y1、y2共有4个交点,请直接写出点P的纵坐标yp的取值范围.
【考点】二次函数综合题.
【专题】代数几何综合题;二次函数图象及其性质;平移、旋转与对称;运算能力;推理能力.
【答案】(1)(1,4);
(2)①y2=﹣x2+4x;
②3≤yp或yp<4.
【分析】(1)根据顶点坐标公式求出该函数图象的顶点的横坐标,代入y1=ax2﹣2ax+a+4求出顶点的纵坐标,即可得抛物线y1的顶点坐标;
(2)①将抛物线y1写成顶点式,求出点B的坐标为(0,3),点A的坐标为(﹣1,0),根据二次函数平移的性质即可得抛物线y2的解析式;
②画出图形,求出抛物线y1和抛物线y2的交点坐标,根据直线l与抛物线y1、y2共有4个交点,即可得点P的纵坐标yp的取值范围.
【解答】解:(1)∵y1=ax2﹣2ax+a+4(a≠0).
该函数图象的顶点的横坐标为:x1,
当x=1时,y1=a﹣2a+a+4=4,
∴抛物线y1的顶点坐标为(1,4);
(2)①当a=﹣1时,该抛物线的解析式为y1=﹣x2+2x+3=﹣(x﹣1)2+4,
令x=0,则y1=3,
令y1=0,则﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
故点B的坐标为(0,3),点A的坐标为(﹣1,0),把y1的图象向右平移1个单位长度,点A与原点O重合,
此时抛物线y2=﹣(x﹣1﹣1)2+4=﹣x2+4x;
②平移的图象如下:
当y1=y2时,﹣x2+2x+3=﹣x2+4x,
解得x,
此时y1=y2=﹣()2+4,
故y1、y2图象的交点C的坐标为(,),
∴P点的纵坐标在介于B点的纵坐标和C点的纵坐标之间移动,在C点的纵坐标和抛物线顶点的纵坐标之间移动,直线l与抛物线y1、y2共有4个交点,
∵点B的坐标为(0,3),抛物线y1的顶点坐标为(1,4),
∴当P的纵坐标为3≤yp或yp<4时,直线l与抛物线y1、y2共有4个交点.
【点评】本题是二次函数综合题,考查二次函数的性质、二次函数图象与几何变换、二次函数图象上点的坐标特征等知识,解题的关键是熟练掌握二次函数平移的性质.
25.(12分)(2022秋 汕尾期中)已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? 是 (填“是”或“否”),∠BOE= 120 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
(2)如图c,在AB和AC上分别截取点B'和C',使AB'=AC',连接B′C′,将△AB'C'绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1)①是,120;
②120°;
(2)当0°<θ<30°时,∠BOE=∠BOC=60°,
当θ=30°时,点B,点O,点E共线.
当30°<θ<180°时,∠BOE=180°﹣∠BOC=180°﹣60°=120°.
【分析】(1)①根据旋转变换的性质以及等边三角形的性质可得AB=AD=AC=AE,∠BAD=∠CAE,然后利用“边角边”证明△ABD与△ACE全等;根据三角形的内角和等于180°求出∠ABD与∠AEC的度数,再根据旋转角为20°求出∠BAE的度数,然后利用四边形的内角和公式求解即可;
②先利用“边角边”证明△BAD和△CAE全等,根据全等三角形对应角相等可得∠ADB=∠AEC,再利用四边形ABOE的内角和等于360°推出∠BOE+∠DAE=180°,再根据等边三角形的每一个角都是60°得到∠DAE=60°,从而得解;
(2)先求出B′C′∥BC,证明△AB′C′是等边三角形,再根据旋转变换的性质可得AD=AE,∠BAD=∠CAE,然后利用“边角边”证明△ABD和△ACE全等,根据全等三角形对应角相等可得∠ABD=∠ACE,再利用三角形的内角和定理求出∠BOC的度数,然后分0°<θ≤30°与30°<θ<180°两种情况求解.
【解答】解:(1)①∵△ADE是由△ABC绕点A旋转θ得到,△ABC是等边三角形,
∴AB=AD=AC=AE,∠BAD=∠CAE=20°,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS);
∵θ=20°,
∴∠ABD=∠AEC(180°﹣20°)=80°,
又∵∠BAE=θ+∠BAC=20°+60°=80°,
∴在四边形ABOE中,∠BOE=360°﹣80°﹣80°﹣80°=120°;
故答案为:是,120;
②由已知得:△ABC和△ADE是全等的等边三角形,
∴AB=AD=AC=AE,
∵△ADE是由△ABC绕点A旋转θ得到的,
∴∠BAD=∠CAE=θ,
∴△BAD≌△CAE,
∴∠ADB=∠AEC,
∵∠ADB+∠ABD+∠BAD=180°,
∴∠AEC+∠ABD+∠BAD=180°,
∵∠ABO+∠AEC+∠BAE+∠BOE=360°,
∵∠BAE=∠BAD+∠DAE,
∴∠DAE+∠BOE=180°,
又∵∠DAE=60°,
∴∠BOE=120°;
(2)如图,∵ABAB′,ACAC′,
∴,
∴B′C′∥BC,
∵△ABC是等边三角形,
∴△AB′C′是等边三角形,
根据旋转变换的性质可得AD=AE,∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∴∠BOC=180°﹣(∠OBC+∠OCB),
=180°﹣(∠OBC+∠ACB+∠ACE),
=180°﹣(∠OBC+∠ACB+∠ABD),
=180°﹣(∠ACB+∠ABC),
=180°﹣(60°+60°),
=60°,
当0°<θ<30°时,∠BOE=∠BOC=60°,
当θ=30°时,点B,点O,点E共线.
当30°<θ<180°时,∠BOE=180°﹣∠BOC=180°﹣60°=120°.
【点评】本题属于几何变换综合题,考查了旋转变换的性质,等边三角形的性质,全等三角形的判定与性质,根据旋转变换的性质找出证明全等三角形的条件是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2025 广陵区一模)实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.|m|<|n| B.m+n>0 C.m﹣n<0 D.mn>0
2.(3分)(2025 浙江模拟)2025年2月12日,中国载人航天工程办公室宣布,载人月球探测任务的登月服命名为“望字”.已知月球距离地球的距离约为384000km,将384000用科学记数法表示为( )
A.3.84×105 B.384×103 C.3.84×103 D.0.384×106
3.(3分)(2024秋 遵义期中)将直角三角板(含30°)和直尺按如图方式摆放,则∠1的度数为( )
A.40° B.45° C.50° D.60°
4.(3分)(2022 华龙区校级模拟)下列各式计算正确的是( )
A.a2+2a3=a5 B.a a2=a3 C.a6÷a2=a3 D.(a2)3=a5
5.(3分)(2023秋 郑州期末)甲、乙两名战士在相同条件下各射击10次,每次命中的环数如下:甲:8,6,7,7,9,10,7,5,4,7;乙:7,9,8,5,6,7,7,6,7,8;以下选项正确的是( )
A.甲的平均数大于乙的平均数
B.甲的方差大于乙的方差
C.甲的中位数大于乙的中位数
D.甲的众数大于乙的众数
6.(3分)(2025 合肥二模)当x>0时,下列函数值y随x增大而增大的是( )
A.y=﹣5x+1 B. C.y=﹣x2 D.y=﹣x2+2x
7.(3分)(2024秋 洞口县期中)方程的根的情况是( )
A.没有实数根
B.两个相等的实数根
C.两个不相等的实数根
D.两个根分别为一个正根,一个负根
8.(3分)(2022 阿克苏地区一模)如图,O的直径AB=8,∠A=30°,点P在线段AB上,则PC的最小值为( )
A.2 B. C.4 D.
9.(3分)(2024 顺庆区二模)数学实践小组测量某路段上一处标识脱落的车辆限高杆MN的高度AB,如图,他们先用测角仪在C处测得点A的仰角∠AEG=30°,然后在D处测得点A的仰角∠AFG=45°,已知点C,D,B在同一条直线上,测角仪离地面高度CE=1m,CD=2m,则AB高( )
A.(2)m B.(1)m C.(3)m D.(2)m
10.(3分)护眼台灯亮度调节的原理是台灯内电路的电压为定值,通过控制可变电阻从而调节台灯的亮度,已知台灯的电流I(A)是电阻R(Ω)(R>0)的反比例函数,其函数图象如图所示,则下列说法正确的是( )
A.
B.该护眼台灯的电压为110V
C.若I≤5A,则R≥44Ω
D.当R=55Ω时,I=6A
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2025 东城区校级模拟)若二次根式有意义,则x的取值范围是 .
12.(3分)(2024 海淀区校级模拟)分式方程的解x= .
13.(3分)计算2025×5.052﹣2025×4.952的结果是 .
14.(3分)(2025 朝阳区一模)图①是小区围墙上的镂空花窗,其形状是扇形的一部分,图②是其示意图(阴影部分为镂空花窗).通过测量得到扇形AOB的圆心角为90°,OA=60cm,点C、D分别为OA、OB上靠近点O的三等分点,则这个镂空花窗的面积为 cm2(结果保留π).
15.(3分)(2024秋 苏州期末)对于一个函数,当自变量x取n时,其函数值y等于3n,我们称n为这个函数的“三倍数”.若二次函数y=x2+7x+2c有且只有一个“三倍数”,则c的值为 .
16.(3分)(2025 杭州一模)菱形ABCD绕点A旋转得到菱形AB'C'D',点B'在BC上,B'C'交CD于点E.若AB=2BB'=4,则CE的长为 .
三.解答题(共9小题,满分72分)
17.(4分)(2025 中宁县二模)解不等式组:.
18.(4分)(2022秋 道外区校级期中)化简求值:(2x+3y)2﹣(2x+y) (2x﹣y),其中x,y.
19.(6分)(2023秋 西城区校级期中)尺规作图,不写作法,保留作图痕迹.
(1)已知△ABC,现将△ABC绕点B逆时针旋转,使点A落在射线BP上,可得△A′C'B.
作法:
①在射线BP上截BA'=BA;
②以点B为圆心,BC长为半径作弧,以点A′为圆心,AC长为半径作弧,两弧在射线BP的右侧交于点C′;
③连接A'C',BC',则△A'C'B即为所求.
经过上述操作可知△A'C'B与△ACB的关系是 ,理由是 .
(2)如图,在直线MN上求作一点P,使点P到射线OA,OB的距离相等.
20.(6分)(2024 黄石开学)在浓度为15%的盐水中加入39千克水和1千克盐,浓度变为10%,这时,再加入多少千克盐,浓度变为20%?
21.(8分)(2025 禄丰市一模)“一寸光阴不可轻,最是书香能致远.”阅读是美好的,阅读是快乐的.某校社团将《西游记》中的四位人物的肖像制成编号为 A、B、C、D的四张卡片(除编号和人物肖像外其余完全相同),活动时学生根据所抽取的卡片来讲述他们在书中的故事.游戏规则如下:先将四张卡片背面朝上,洗匀放好,小东先从中随机抽取一张,记卡片上的人物为x,再把剩下的3张卡片洗匀后,背面向上放好,小华再从3张卡片中随机抽取一张,记卡片上的人物为y.若他们取出的两张卡片上对应的人物为师徒关系,则由小东讲,否则由小华讲.
(1)用列表法或画树状图法中的一种方法,列出(x,y)所有可能出现的结果;
(2)你认为这个游戏是否公平?请说明理由.
22.(10分)(2023 长安区一模)如图,在Rt△ABC中,∠BAC=90°,O为边BC上一点,以OB为半径的⊙O与AC相切于点D,连接BD.
(1)求证:BD平分∠ABC;
(2)连接AO,若∠AOB=90°,AB=4,求⊙O的半径.
23.(10分)(2024 广西三模)综合与实践
小涛在学习过程中发现:周长为定值的矩形中面积最大的是正方形.那么,面积为定值的矩形中,其周长的取值范围会如何呢?小涛尝试从函数的角度进行探究:
【建立模型】设一矩形的面积为4,周长为m,相邻的两边长分别为x,y,则,即,那么满足要求的(x,y)可以看作是函数与的图象在第 象限内的公共点坐标.
【画出图象】
在同一平面直角坐标系中画出函数y=﹣x,的图象
则的图象可以看成是y=﹣x的图象向上平移 个单位长度得到.
【研究图象】平移直线,观察两函数的图象.
①当直线y=﹣x平移到与函数的图象有唯一公共点的位置时,直接写出公共点的坐标及周长m的值.
②在直线平移的过程中,两函数图象公共点的个数还有什么情况?请直接写出公共点的个数及对应周长m的取值范围.
【结论运用】求面积为9的矩形的周长m的取值范围.
24.(12分)(2022 济源一模)已知抛物线y1=ax2﹣2ax+a+4(a≠0).
(1)求抛物线y1的顶点坐标;
(2)如图,当a=﹣1时,抛物线y1与x轴的负半轴、y轴分别交于点A、点B.
①将抛物线y1向右平移,使点A与原点重合.求平移后的抛物线y2的解析式;
②点P为抛物线y1上的一个动点,过点P作x轴的平行线l,若点P在由点B向顶点运动的过程中,直线l与抛物线y1、y2共有4个交点,请直接写出点P的纵坐标yp的取值范围.
25.(12分)(2022秋 汕尾期中)已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? (填“是”或“否”),∠BOE= 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
(2)如图c,在AB和AC上分别截取点B'和C',使AB'=AC',连接B′C′,将△AB'C'绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
2025年广州市中考数学模拟预测卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)(2025 广陵区一模)实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.|m|<|n| B.m+n>0 C.m﹣n<0 D.mn>0
【考点】实数与数轴;绝对值.
【专题】实数;运算能力.
【答案】B
【分析】根据实数m,n在数轴上的对应点的位置得到m和n的取值范围,逐个进行判断即可.
【解答】解:由题意得:﹣2<n<﹣1,3<m<4,m>n,
A、∵3<|m|<4,1<|n|<2,∴|m|>|n|,故A选项错误;
B、∵|m|>|n|,m+n>0,故B选项正确;
C、∵m>n,∴m﹣n>0,故C选项错误;
D、∵﹣2<n<﹣1,3<m<4,∴mn<0,故D选项错误.
故选:B.
【点评】本题考查了实数与数轴,绝对值,熟练掌握实数与数轴的对应关系是解题的关键.
2.(3分)(2025 浙江模拟)2025年2月12日,中国载人航天工程办公室宣布,载人月球探测任务的登月服命名为“望字”.已知月球距离地球的距离约为384000km,将384000用科学记数法表示为( )
A.3.84×105 B.384×103 C.3.84×103 D.0.384×106
【考点】科学记数法—表示较大的数.
【专题】实数;符号意识.
【答案】A.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:384000=3.84×105.
故选:A.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.(3分)(2024秋 遵义期中)将直角三角板(含30°)和直尺按如图方式摆放,则∠1的度数为( )
A.40° B.45° C.50° D.60°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】D
【分析】由两直线平行,内错角相等,即可得到答案.
【解答】解:∵AB∥CD,
∴∠1=∠2=60°.
故选:D.
【点评】本题考查平行线的性质,关键是掌握两直线平行,内错角相等.
4.(3分)(2022 华龙区校级模拟)下列各式计算正确的是( )
A.a2+2a3=a5 B.a a2=a3 C.a6÷a2=a3 D.(a2)3=a5
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】B
【分析】根据幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减;同底数幂相乘,底数不变指数相加,对各选项分析判断利用排除法求解.
【解答】解:A、a2与2a3不是同类项,不能合并,故本选项错误;
B、a a2=a1+2=a3,故本选项正确;
C、a6÷a2=a6﹣2=a4,故本选项错误;
D、(a2)3=a2×3=a6,故本选项错误.
故选:B.
【点评】本题考查了同底数幂的除法,同底数幂的乘法,幂的乘方的性质,熟记性质并理清指数的变化是解题的关键.
5.(3分)(2023秋 郑州期末)甲、乙两名战士在相同条件下各射击10次,每次命中的环数如下:甲:8,6,7,7,9,10,7,5,4,7;乙:7,9,8,5,6,7,7,6,7,8;以下选项正确的是( )
A.甲的平均数大于乙的平均数
B.甲的方差大于乙的方差
C.甲的中位数大于乙的中位数
D.甲的众数大于乙的众数
【考点】方差;算术平均数;中位数;众数.
【专题】统计的应用;应用意识.
【答案】B
【分析】本题考查平均数、方差、中位数和众数,解题的关键是掌握相关知识.分别求出甲、乙的平均数、方差、中位数、众数,即可求解.
【解答】解:A、∵7,7,
∴甲的平均数等于乙的平均数,A错误;
B、∵2.8,
2,
∴甲的方差大于乙的方差,B正确;
C、∵甲的中为数为:7,乙的中位数为:7,
∴甲的中位数等于乙的中位数,C错误;
D、∵甲的众数为7,乙的众数为7,
∴甲的众数等于乙的众数,D错误;
故选:B.
【点评】此题考查了平均数、中位数、众数和方差的意义,解题的关键是正确理解各概念的含义.
6.(3分)(2025 合肥二模)当x>0时,下列函数值y随x增大而增大的是( )
A.y=﹣5x+1 B. C.y=﹣x2 D.y=﹣x2+2x
【考点】反比例函数的性质;二次函数的性质;一次函数的性质.
【专题】一次函数及其应用;反比例函数及其应用;二次函数图象及其性质;推理能力.
【答案】B
【分析】分别根据一次函数的性质、反比例函数的性质、二次函数的性质逐项分析即可得出结论.
【解答】解:A、一次函数y=﹣5x+1的﹣5<0,函数值y随x增大而减小,不符合题意;
B、反比例函数的﹣5<0,当x>0时,函数值y随x增大而增大,正确,符合题意;
C、二次函数y=﹣x2的﹣1<0,开口向下,当x>0时,函数值y随x增大而减小,不符合题意;
D、二次函数y=﹣x2+2x的﹣1<0,开口向下,对称轴x=1,当x>1时,函数值y随x增大而减小,不符合题意.
故选:B.
【点评】本题考查了一次函数的性质、反比例函数的性质、二次函数的性质,熟知以上知识是解题的关键.
7.(3分)(2024秋 洞口县期中)方程的根的情况是( )
A.没有实数根
B.两个相等的实数根
C.两个不相等的实数根
D.两个根分别为一个正根,一个负根
【考点】根的判别式.
【专题】一元二次方程及应用;运算能力.
【答案】B
【分析】根据一元二次方程根的判别式即可解决问题.
【解答】解:由题知,
原方程可化为2x2x+3=0,
则0,
所以原方程有两个相等的实数根.
故选:B.
【点评】本题主要考查了根的判别式,熟知一元二次方程根的判别式是解题的关键.
8.(3分)(2022 阿克苏地区一模)如图,O的直径AB=8,∠A=30°,点P在线段AB上,则PC的最小值为( )
A.2 B. C.4 D.
【考点】圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】B
【分析】连接BC,由圆周角定理得出∠ACB=90°,由∠A=30°得出BC=4,求出AC=4,当CP⊥AB时,CP最小,CPAC=2得出答案.
【解答】解:连接BC,
∵AB是直径,
∴∠ACB=90°,
∵AB=8,∠A=30°,
∴BC=4,AC=4,
当CP⊥AB时,PC最小,
∵∠A=30°,
∴CPAC=2.
故选:B.
【点评】本题主要考查了圆周角定理,熟练掌握圆周角定理是解题的关键.
9.(3分)(2024 顺庆区二模)数学实践小组测量某路段上一处标识脱落的车辆限高杆MN的高度AB,如图,他们先用测角仪在C处测得点A的仰角∠AEG=30°,然后在D处测得点A的仰角∠AFG=45°,已知点C,D,B在同一条直线上,测角仪离地面高度CE=1m,CD=2m,则AB高( )
A.(2)m B.(1)m C.(3)m D.(2)m
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力;应用意识.
【答案】A
【分析】延长EF,交AB于点H,设HF=x米,在Rt△AHF中,可得AH=HF=x米,在Rt△AHE中,tan30°,求出x的值,进而可得出答案.
【解答】解:延长EF,交AB于点H,
由题意得,HB=DF=CE=1米,CD=FE=2米,
设HF=x米,
则EH=HF+FE=(x+2)米,
在Rt△AHF中,∠AFH=45°,
∴∠FAH=45°,
∴AH=HF=x米,
在Rt△AHE中,tan30°,
解得x1,
∴AB=AH+BH1+1(米).
故选:A.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
10.(3分)护眼台灯亮度调节的原理是台灯内电路的电压为定值,通过控制可变电阻从而调节台灯的亮度,已知台灯的电流I(A)是电阻R(Ω)(R>0)的反比例函数,其函数图象如图所示,则下列说法正确的是( )
A.
B.该护眼台灯的电压为110V
C.若I≤5A,则R≥44Ω
D.当R=55Ω时,I=6A
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】C
【分析】依据题意,先求出反比例函数的解析式,然后根据反比例函数性质逐项分析判断即可.
【解答】解:由题意,I,
∴U=2×110=220.
∴该反比例函数的解析式为I,故A错误.
∴该护眼台灯的电压为220V,故B错误.
若I≤5A,
∴5.
∴R≥44Ω,故C正确.
又当R=55Ω时,I=220÷55=4(A),
∴D错误.
故选:C.
【点评】本题主要考查了反比例函数的应用,解题时要熟练掌握并能灵活运用反比例函数的性质是关键.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2025 东城区校级模拟)若二次根式有意义,则x的取值范围是 x .
【考点】二次根式有意义的条件;解一元一次不等式.
【专题】二次根式;一元一次不等式(组)及应用;运算能力.
【答案】见试题解答内容
【分析】先根据二次根式有意义的条件得出5x﹣1≥0,再求出x的取值范围即可.
【解答】解:要使二次根式有意义,必须5x﹣1≥0,
解得:x,
所以x的取值范围是x.
故答案为:x.
【点评】本题考查了二次根式有意义的条件和解一元一次不等式,能根据二次根式有意义的条件得出5x﹣1≥0是解此题的关键.
12.(3分)(2024 海淀区校级模拟)分式方程的解x= .
【考点】解分式方程.
【专题】分式方程及应用;运算能力.
【答案】见试题解答内容
【分析】利用解分式方程的一般步骤解答即可.
【解答】解:去分母得:
2x=3﹣2×2(x﹣1),
去括号得:
2x=3﹣4x+4,
移项,合并同类项得:
6x=7,
∴x,
经检验,x是原方程的解,
∴x.
故答案为:.
【点评】本题主要考查了分式方程的解法,熟练掌握分式方程的解法的一般步骤是解题的关键.
13.(3分)计算2025×5.052﹣2025×4.952的结果是 2025 .
【考点】提公因式法与公式法的综合运用.
【专题】计算题;运算能力.
【答案】2025.
【分析】先提公因式法2025,再运用平方差公式计算即可.
【解答】解:原式=2025×(5.052﹣4.952)
=2025×(5.05+4.95)×(5.05﹣4.95)
=2025×10×0.1
=2025.
故答案为:1.
【点评】本题考查了提公因式法与公式法的综合运用,掌握因式分解的提公因式法、公式法是解决本题的关键.
14.(3分)(2025 朝阳区一模)图①是小区围墙上的镂空花窗,其形状是扇形的一部分,图②是其示意图(阴影部分为镂空花窗).通过测量得到扇形AOB的圆心角为90°,OA=60cm,点C、D分别为OA、OB上靠近点O的三等分点,则这个镂空花窗的面积为 (900π﹣200) cm2(结果保留π).
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(900π﹣200).
【分析】利用三角形和扇形的面积公式分别求出△COD和扇形AOB的面积,再根据“镂空花窗的面积=扇形AOB的面积﹣△COD的面积”计算即可.
【解答】解:∵OA=OB=60cm,点C、D分别为OA、OB上靠近点O的三等分点,
∴OC=OD60=20(cm),
∴SRt△COD OC OD 20×20=200(cm2),S扇形AOBπ×602=900π(cm2),
∴S阴影=S扇形AOB﹣SRt△COD =(900π﹣200)(cm2).
故答案为:(900π﹣200).
【点评】本题考查扇形面积的计算,掌握三角形和扇形面积计算公式是解题的关键.
15.(3分)(2024秋 苏州期末)对于一个函数,当自变量x取n时,其函数值y等于3n,我们称n为这个函数的“三倍数”.若二次函数y=x2+7x+2c有且只有一个“三倍数”,则c的值为 2 .
【考点】二次函数的性质.
【专题】新定义;二次函数图象及其性质;运算能力.
【答案】2.
【分析】先设二次函数y=x2+7x+2c的三倍点为(m,3m),然后即可得到方程m2+4m+2c=0,再根据二次函数y=x2+7x+2c有且只有一个“三倍数”,可知方程m2+4m+2c=0有两个相等的实数根,从而可以求得c的值.
【解答】解:设二次函数y=x2+7x+2c的三倍点为(m,3m),
则3m=m2+7m+2c,
∴m2+7m+2c﹣3m=0,
∴m2+4m+2c=0,
∵二次函数y=x2+7x+2c有且只有一个“三倍数”,
∴Δ=42﹣4×1×2c=0,
解得c=2,
故答案为:2.
【点评】本题考查二次函数的性质、新定义,解答本题的关键是明确题意,利用二次函数与方程的关系解答.
16.(3分)(2025 杭州一模)菱形ABCD绕点A旋转得到菱形AB'C'D',点B'在BC上,B'C'交CD于点E.若AB=2BB'=4,则CE的长为 .
【考点】旋转的性质;菱形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力;应用意识.
【答案】.
【分析】如图,过点C作CF∥C′D′,交B′C′于点F,根据等腰三角形的性质得到∠B=∠AB′B,根据平行线的性质得到∠B′CF=∠AB′B,根据相似三角形的性质得到FC,由旋转可知DD′=BB′=2求得C′D=2,又由CF∥C′D,根据相似三角形的性质即可得到结论.
【解答】解:如图,过点C作CF∥C′D′,交B′C′于点F,
∵菱形AB′C′D′中,AB′∥C′D′,
∴AB′∥CF∥C′D′,
∵AB=AB′,
∴∠B=∠AB′B,
∵∠AB′C′=∠B,
∴∠FB′C=∠BAB′,
∵AB′∥FC,
∴∠B′CF=∠AB′B,
∵AB=2BB'=4,
∴B′C=BB′=2,
∴△ABB′∽△B′CF,
∴,
∴,
∴FC=1,
由旋转可知,△ABB′≌△ADD′,
∴DD′=BB′=2,
∴C′D=2,
又由CF∥C′D,
∴△C′DE∽△FCE,
∴,
∴,
∴,
∴CE.
故答案为:.
【点评】本题主要考查旋转的性质,菱形的性质,等腰三角形三线合一,相似三角形的性质与判定,解直角三角形的应用等,正确地作出辅助线是解题关键.
三.解答题(共9小题,满分72分)
17.(4分)(2025 中宁县二模)解不等式组:.
【考点】解一元一次不等式组.
【专题】一元一次不等式(组)及应用;运算能力.
【答案】.
【分析】根据解一元一次不等式组的步骤,对所给不等式组进行求解即可.
【解答】解:,
解不等式①得,x≤3;
解不等式②得,x,
所以不等式组的解集为:.
【点评】本题主要考查了解一元一次不等式组,熟知解一元一次不等式组的步骤是解题的关键.
18.(4分)(2022秋 道外区校级期中)化简求值:(2x+3y)2﹣(2x+y) (2x﹣y),其中x,y.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】12xy+10y2,.
【分析】先用平方差公式和完全平方公式展开,再去括号,合并同类项,化简后将x,y的值代入计算即可.
【解答】解:原式=4x2+12xy+9y2﹣(4x2﹣y2)
=4x2+12xy+9y2﹣4x2+y2
=12xy+10y2,
当x,y时,
原式=12()+10×()2
=﹣2+10
=﹣2
.
【点评】本题考查整式化简求值,解题的关键是掌握平方差公式和完全平方公式,把所求式子化简.
19.(6分)(2023秋 西城区校级期中)尺规作图,不写作法,保留作图痕迹.
(1)已知△ABC,现将△ABC绕点B逆时针旋转,使点A落在射线BP上,可得△A′C'B.
作法:
①在射线BP上截BA'=BA;
②以点B为圆心,BC长为半径作弧,以点A′为圆心,AC长为半径作弧,两弧在射线BP的右侧交于点C′;
③连接A'C',BC',则△A'C'B即为所求.
经过上述操作可知△A'C'B与△ACB的关系是 △A'C'B≌△ACB ,理由是 SSS .
(2)如图,在直线MN上求作一点P,使点P到射线OA,OB的距离相等.
【考点】作图﹣旋转变换;角平分线的性质;作图—基本作图.
【专题】图形的全等;平移、旋转与对称;几何直观.
【答案】(1)△A'C'B≌△ACB;SSS.
(2)见解答.
【分析】(1)根据全等三角形的判定可得答案.
(2)作∠AOB的平分线,交MN于点P,则点P即为所求.
【解答】解:(1)由作图可得,BC=BC',AC=A'C',
∵BA'=BA,
∴△A'C'B≌△ACB(SSS).
故答案为:△A'C'B≌△ACB;SSS.
(2)如图2,点P即为所求.
【点评】本题考查作图﹣基本作图、角平分线的性质、全等三角形的判定,熟练掌握角平分线的性质、全等三角形的判定是解答本题的关键.
20.(6分)(2024 黄石开学)在浓度为15%的盐水中加入39千克水和1千克盐,浓度变为10%,这时,再加入多少千克盐,浓度变为20%?
【考点】一元一次方程的应用;百分数的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】再加入12.5千克盐,浓度变为20%.
【分析】先设原来有15%的盐水x千克,根据“浓度变为10%”列方程求出x的值,再依据新浓度列出算式计算即可.
【解答】解:设原来有15%的盐水x千克,
由题意,得(15% x+1)÷(x+39+1)=10%,
解得:x=60,
(60+39+1)(1﹣10% )÷(1﹣20% )﹣(60+39+1)
=100×(1﹣0.1)÷(1﹣0.2)﹣100
=90÷0.8﹣100
=112.5﹣100
=12.5(千克),
答:再加入12.5千克盐,浓度变为20%.
【点评】本题考查百分数的应用,一元一次方程的应用,解题的关键是读懂题意,列出方程,掌握解一元一次方程的方法是解题的关键.
21.(8分)(2025 禄丰市一模)“一寸光阴不可轻,最是书香能致远.”阅读是美好的,阅读是快乐的.某校社团将《西游记》中的四位人物的肖像制成编号为 A、B、C、D的四张卡片(除编号和人物肖像外其余完全相同),活动时学生根据所抽取的卡片来讲述他们在书中的故事.游戏规则如下:先将四张卡片背面朝上,洗匀放好,小东先从中随机抽取一张,记卡片上的人物为x,再把剩下的3张卡片洗匀后,背面向上放好,小华再从3张卡片中随机抽取一张,记卡片上的人物为y.若他们取出的两张卡片上对应的人物为师徒关系,则由小东讲,否则由小华讲.
(1)用列表法或画树状图法中的一种方法,列出(x,y)所有可能出现的结果;
(2)你认为这个游戏是否公平?请说明理由.
【考点】游戏公平性;列表法与树状图法.
【专题】概率及其应用;数据分析观念.
【答案】(1)见解答;
(2)游戏规则公平,理由见解答.
【分析】(1)列表可得所有等可能结果;
(2)从表格中得出取出的两张卡片上对应的人物为师徒关系的结果数,继而求出小东、小华讲的概率,从而得出答案.
【解答】解:(1)列表如下:
A B C D
A (B,A) (C,A) (D,A)
B (A,B) (C,B) (D,B)
C (A,C) (B,C) (D,C)
D (A,D) (B,D) (C,D)
共有12种等可能的结果;
(2)游戏规则公平,理由如下:
由表知,他们取出的两张卡片上对应的人物为师徒关系的结果有6种,
∴由小东讲的概率为,
则由小华讲的概率为1,
∵,
∴此游戏规则公平.
【点评】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
22.(10分)(2023 长安区一模)如图,在Rt△ABC中,∠BAC=90°,O为边BC上一点,以OB为半径的⊙O与AC相切于点D,连接BD.
(1)求证:BD平分∠ABC;
(2)连接AO,若∠AOB=90°,AB=4,求⊙O的半径.
【考点】相似三角形的判定与性质;垂径定理;圆周角定理;切线的性质.
【专题】等腰三角形与直角三角形;与圆有关的位置关系;图形的相似;运算能力;推理能力.
【答案】(1)证明见解答;
(2)⊙O的半径为22.
【分析】(1)连接OD,则OD=OB,得∠ODB=∠CBD,由切线的性质得∠ODC=∠BAC=90°,则DO∥AB,所以∠ODB=∠ABD,则∠CBD=∠ABD,所以BD平分∠ABC;
(2)设OB=DO=r,由OD∥AB,得△DOC∽△ABC,则,所以DO CB=AB CO,再证明△COD≌△ABO,得CO=AB=4,于是得r(4+r)=4×4,解方程求出符合题意的r的值即可.
【解答】(1)证明:连接OD,则OD=OB,
∴∠ODB=∠CBD,
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ODC=∠BAC=90°,
∴DO∥AB,
∴∠ODB=∠ABD,
∴∠CBD=∠ABD,
∴BD平分∠ABC.
(2)解:设OB=DO=r,
∵OD∥AB,
∴△DOC∽△ABC,
∴,
∴DO CB=AB CO,
∵∠COD=∠ABO,DO=OB,∠ODC=∠BAC=90°,
∴△COD≌△ABO(ASA),
∴CO=AB=4,
∴r(4+r)=4×4,
解得r1=22,r2=﹣22(不符合题意,舍去),
∴⊙O的半径为22.
【点评】此题重点考查等腰三角形的性质、平行线的判定与性质、角平分线的定义、切线的性质、相似三角形的判定与性质等知识,正确地作出所需要的辅助线是解题的关键.
23.(10分)(2024 广西三模)综合与实践
小涛在学习过程中发现:周长为定值的矩形中面积最大的是正方形.那么,面积为定值的矩形中,其周长的取值范围会如何呢?小涛尝试从函数的角度进行探究:
【建立模型】设一矩形的面积为4,周长为m,相邻的两边长分别为x,y,则,即,那么满足要求的(x,y)可以看作是函数与的图象在第 一 象限内的公共点坐标.
【画出图象】
在同一平面直角坐标系中画出函数y=﹣x,的图象
则的图象可以看成是y=﹣x的图象向上平移 个单位长度得到.
【研究图象】平移直线,观察两函数的图象.
①当直线y=﹣x平移到与函数的图象有唯一公共点的位置时,直接写出公共点的坐标及周长m的值.
②在直线平移的过程中,两函数图象公共点的个数还有什么情况?请直接写出公共点的个数及对应周长m的取值范围.
【结论运用】求面积为9的矩形的周长m的取值范围.
【考点】反比例函数综合题.
【专题】代数综合题;运算能力;推理能力.
【答案】【建立模型】一;
【画出图象】;
【研究图象】①(2,2),8;
②0个交点时,0<m<8;2个交点时,m>8;1个交点时,m=8;
【结论运用】m≥12.
【分析】【建立模型】由x>0,y>0,可得(x,y)在第一象限;
【画出图象】求出y=﹣x与x轴的交点坐标,即可求解;
【研究图象】①联立方程组,可求解;②在直线平移过程中,交点个数有:0个、1个、2个三种情况,结合图象可求解;
【结论运用】联立方程组,可得2x2﹣mx+18=0,由根的判别式可求解.
【解答】解:【建立模型】x,y都是边长,因此,都是正数,
故点(x,y)在第一象限,
故答案为:一;
【画出图象】∵y=﹣x与x轴的交点为(,0),
∴y=﹣x+的图象可以看成是由y=﹣x的图象向右平移个单位长度得到,
故答案为:;
【研究图象】①联立方程组可得,
整理得:x2mx+4=0,
∵两图象有唯一交点,
∴Δm2﹣16=0,
∴m=8,
∴x28x+4=0,
解得:x=2,
∴交点坐标为(2,2),
故答案为:(2,2),8;
②由①知:0个交点时,0<m<8;2个交点时,m>8;1个交点时,m=8;
【结论运用】设相邻的两边长为x、y,则x y=9,2(x+y)=m,即y,y=﹣x,
联立方程组可得,
整理得:2x2﹣mx+18=0,
∵两函数有交点,
∴Δ=m2﹣4×2×18≥0,
解得m≥12或m≤﹣12(不符合题意,舍去),
∴m≥12.
【点评】本题属于反比例函数综合题,考查了反比例函数的性质,一次函数的性质,矩形的性质等知识,解题的关键是理解题意,学会利用数形结合的思想解决问题,属于中考压轴题.
24.(12分)(2022 济源一模)已知抛物线y1=ax2﹣2ax+a+4(a≠0).
(1)求抛物线y1的顶点坐标;
(2)如图,当a=﹣1时,抛物线y1与x轴的负半轴、y轴分别交于点A、点B.
①将抛物线y1向右平移,使点A与原点重合.求平移后的抛物线y2的解析式;
②点P为抛物线y1上的一个动点,过点P作x轴的平行线l,若点P在由点B向顶点运动的过程中,直线l与抛物线y1、y2共有4个交点,请直接写出点P的纵坐标yp的取值范围.
【考点】二次函数综合题.
【专题】代数几何综合题;二次函数图象及其性质;平移、旋转与对称;运算能力;推理能力.
【答案】(1)(1,4);
(2)①y2=﹣x2+4x;
②3≤yp或yp<4.
【分析】(1)根据顶点坐标公式求出该函数图象的顶点的横坐标,代入y1=ax2﹣2ax+a+4求出顶点的纵坐标,即可得抛物线y1的顶点坐标;
(2)①将抛物线y1写成顶点式,求出点B的坐标为(0,3),点A的坐标为(﹣1,0),根据二次函数平移的性质即可得抛物线y2的解析式;
②画出图形,求出抛物线y1和抛物线y2的交点坐标,根据直线l与抛物线y1、y2共有4个交点,即可得点P的纵坐标yp的取值范围.
【解答】解:(1)∵y1=ax2﹣2ax+a+4(a≠0).
该函数图象的顶点的横坐标为:x1,
当x=1时,y1=a﹣2a+a+4=4,
∴抛物线y1的顶点坐标为(1,4);
(2)①当a=﹣1时,该抛物线的解析式为y1=﹣x2+2x+3=﹣(x﹣1)2+4,
令x=0,则y1=3,
令y1=0,则﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
故点B的坐标为(0,3),点A的坐标为(﹣1,0),把y1的图象向右平移1个单位长度,点A与原点O重合,
此时抛物线y2=﹣(x﹣1﹣1)2+4=﹣x2+4x;
②平移的图象如下:
当y1=y2时,﹣x2+2x+3=﹣x2+4x,
解得x,
此时y1=y2=﹣()2+4,
故y1、y2图象的交点C的坐标为(,),
∴P点的纵坐标在介于B点的纵坐标和C点的纵坐标之间移动,在C点的纵坐标和抛物线顶点的纵坐标之间移动,直线l与抛物线y1、y2共有4个交点,
∵点B的坐标为(0,3),抛物线y1的顶点坐标为(1,4),
∴当P的纵坐标为3≤yp或yp<4时,直线l与抛物线y1、y2共有4个交点.
【点评】本题是二次函数综合题,考查二次函数的性质、二次函数图象与几何变换、二次函数图象上点的坐标特征等知识,解题的关键是熟练掌握二次函数平移的性质.
25.(12分)(2022秋 汕尾期中)已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? 是 (填“是”或“否”),∠BOE= 120 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
(2)如图c,在AB和AC上分别截取点B'和C',使AB'=AC',连接B′C′,将△AB'C'绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1)①是,120;
②120°;
(2)当0°<θ<30°时,∠BOE=∠BOC=60°,
当θ=30°时,点B,点O,点E共线.
当30°<θ<180°时,∠BOE=180°﹣∠BOC=180°﹣60°=120°.
【分析】(1)①根据旋转变换的性质以及等边三角形的性质可得AB=AD=AC=AE,∠BAD=∠CAE,然后利用“边角边”证明△ABD与△ACE全等;根据三角形的内角和等于180°求出∠ABD与∠AEC的度数,再根据旋转角为20°求出∠BAE的度数,然后利用四边形的内角和公式求解即可;
②先利用“边角边”证明△BAD和△CAE全等,根据全等三角形对应角相等可得∠ADB=∠AEC,再利用四边形ABOE的内角和等于360°推出∠BOE+∠DAE=180°,再根据等边三角形的每一个角都是60°得到∠DAE=60°,从而得解;
(2)先求出B′C′∥BC,证明△AB′C′是等边三角形,再根据旋转变换的性质可得AD=AE,∠BAD=∠CAE,然后利用“边角边”证明△ABD和△ACE全等,根据全等三角形对应角相等可得∠ABD=∠ACE,再利用三角形的内角和定理求出∠BOC的度数,然后分0°<θ≤30°与30°<θ<180°两种情况求解.
【解答】解:(1)①∵△ADE是由△ABC绕点A旋转θ得到,△ABC是等边三角形,
∴AB=AD=AC=AE,∠BAD=∠CAE=20°,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS);
∵θ=20°,
∴∠ABD=∠AEC(180°﹣20°)=80°,
又∵∠BAE=θ+∠BAC=20°+60°=80°,
∴在四边形ABOE中,∠BOE=360°﹣80°﹣80°﹣80°=120°;
故答案为:是,120;
②由已知得:△ABC和△ADE是全等的等边三角形,
∴AB=AD=AC=AE,
∵△ADE是由△ABC绕点A旋转θ得到的,
∴∠BAD=∠CAE=θ,
∴△BAD≌△CAE,
∴∠ADB=∠AEC,
∵∠ADB+∠ABD+∠BAD=180°,
∴∠AEC+∠ABD+∠BAD=180°,
∵∠ABO+∠AEC+∠BAE+∠BOE=360°,
∵∠BAE=∠BAD+∠DAE,
∴∠DAE+∠BOE=180°,
又∵∠DAE=60°,
∴∠BOE=120°;
(2)如图,∵ABAB′,ACAC′,
∴,
∴B′C′∥BC,
∵△ABC是等边三角形,
∴△AB′C′是等边三角形,
根据旋转变换的性质可得AD=AE,∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∴∠BOC=180°﹣(∠OBC+∠OCB),
=180°﹣(∠OBC+∠ACB+∠ACE),
=180°﹣(∠OBC+∠ACB+∠ABD),
=180°﹣(∠ACB+∠ABC),
=180°﹣(60°+60°),
=60°,
当0°<θ<30°时,∠BOE=∠BOC=60°,
当θ=30°时,点B,点O,点E共线.
当30°<θ<180°时,∠BOE=180°﹣∠BOC=180°﹣60°=120°.
【点评】本题属于几何变换综合题,考查了旋转变换的性质,等边三角形的性质,全等三角形的判定与性质,根据旋转变换的性质找出证明全等三角形的条件是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
