2024-2025学年浙教版八年级数学下册月考测试卷(含答案)
文档属性
| 名称 | 2024-2025学年浙教版八年级数学下册月考测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 295.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 10:01:35 | ||
图片预览


文档简介
2024-2025学年八年级数学下册月考测试卷
(浙江专用)
【5月】
测试范围:第1~5单元(浙教版 八年级下册)。
考试时间:120分钟 满分:120分
题号 一 二 三 总分
评分
注意事项:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分。答卷前,考生务必将自己的姓名、准考
证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
【卷I】基础知识与基本能力
阅卷人
得分
一、反复比较,合理选择(每题3分,共30分)
1. 下列交通标志中是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2. 估计的运算结果在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
3. 面试时,小王的基本知识、表达能力、工作态度的得分分别是89分、78分、85分,若依次按40%, 30%, 30%的比例确定面试成绩,则小王的面试成绩为( )
A. 82分 B. 84.5分 C. 85.5分 D. 85分
4. 下列命题是假命题的是( )
A.若|a|=|b|,则a=b
B.两直线平行,同位角相等
C.对顶角相等
D.若b2﹣4ac>0,则方程ax2+bx+c=0(a≠0)有两个不等的实数根
5. 如图放置的五块拼图中,①②③为正方形,④⑤为等腰直角三角形,若正方形③的面积为2,则正方形②的面积为( )
A.4 B.6 C.8 D.12
6. 将式子根式外的因式移到根式内的结果是( )
A. B. C. D.
7. 用一条长40cm的绳子怎样围成一个面积为75cm2的矩形?设矩形的一边为x米,根据题意,可列方程为( )
A.x(40-x)=75 B.x(20-x)=75 C.x(x+40)=75 D.x(x+20)=7
8. 某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛,而这9名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的( )
A.平均数 B.中位数 C.众数 D.方差
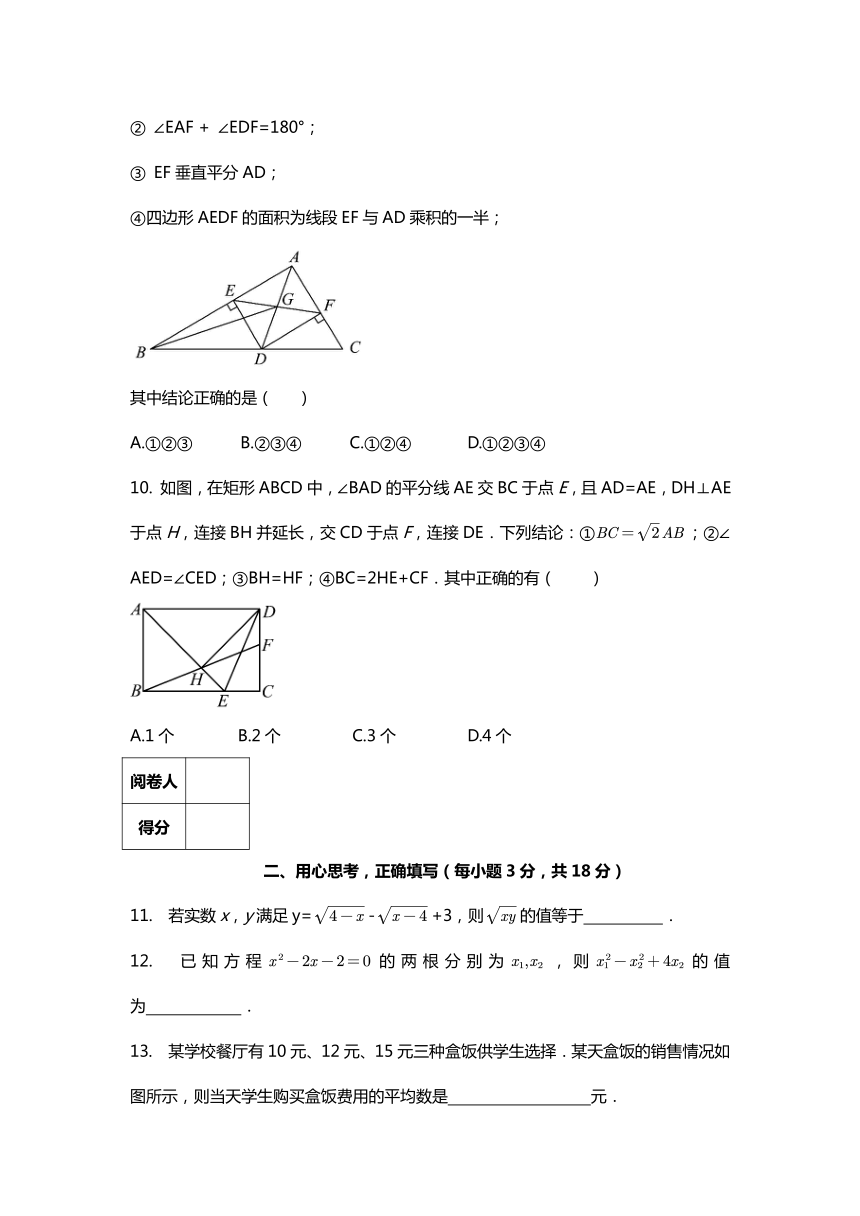
9. 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF交AD于点G.下列结论:
① AE=AF;
② ∠EAF + ∠EDF=180°;
③ EF垂直平分AD;
④四边形AEDF的面积为线段EF与AD乘积的一半;
其中结论正确的是( )
A.①②③ B.②③④ C.①②④ D.①②③④
10. 如图,在矩形ABCD中,∠BAD的平分线AE交BC于点E,且AD=AE,DH⊥AE于点H,连接BH并延长,交CD于点F,连接DE.下列结论:①;②∠AED=∠CED;③BH=HF;④BC=2HE+CF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
阅卷人
得分
二、用心思考,正确填写(每小题3分,共18分)
11. 若实数x,y满足y=-+3,则的值等于 .
12. 已知方程的两根分别为,则的值为 .
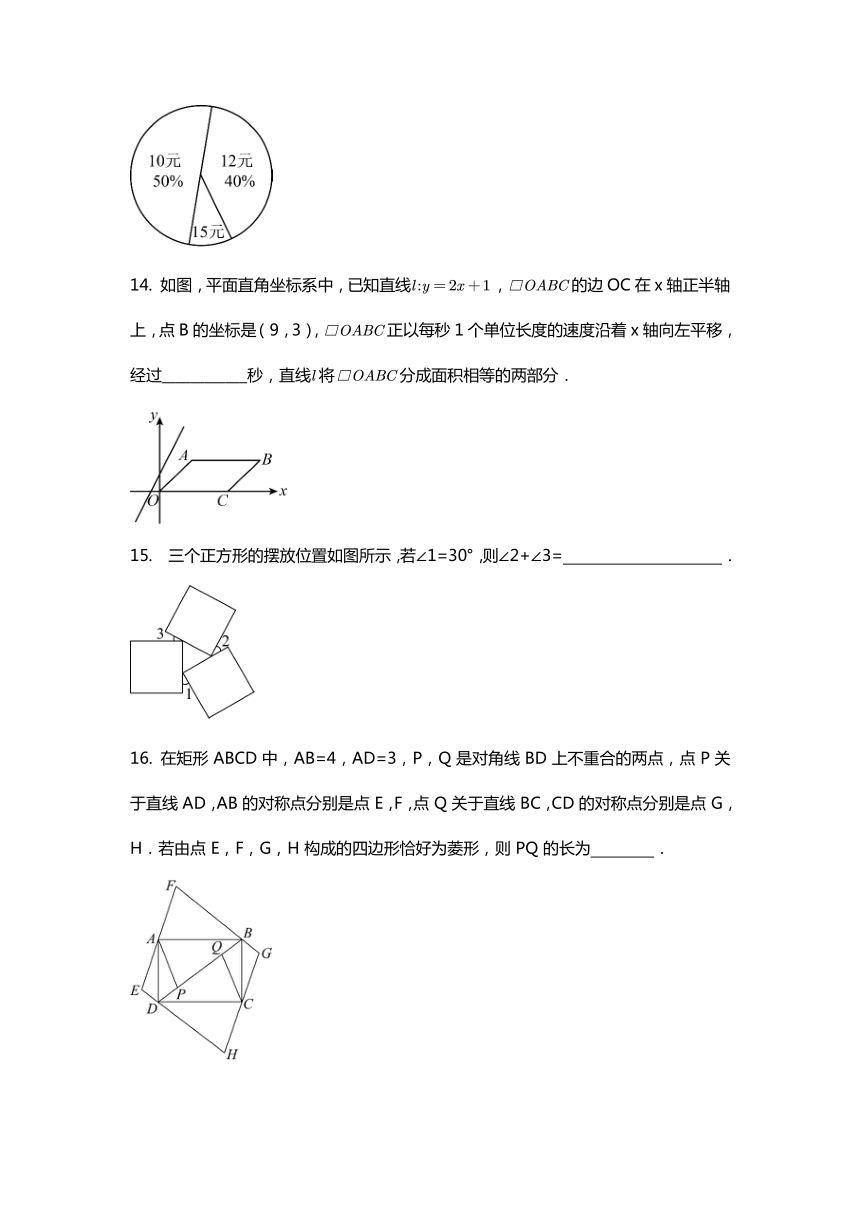
13. 某学校餐厅有10元、12元、15元三种盒饭供学生选择.某天盒饭的销售情况如图所示,则当天学生购买盒饭费用的平均数是 元.
14. 如图,平面直角坐标系中,已知直线,的边OC在x轴正半轴上,点B的坐标是(9,3),正以每秒1个单位长度的速度沿着x轴向左平移,经过____________秒,直线将分成面积相等的两部分.
15. 三个正方形的摆放位置如图所示,若∠1=30°,则∠2+∠3= .
16. 在矩形 ABCD 中,AB=4,AD=3,P,Q 是对角线 BD 上不重合的两点,点 P 关于直线 AD,AB 的对称点分别是点 E,F,点 Q 关于直线 BC,CD 的对称点分别是点 G,H.若由点 E,F,G,H 构成的四边形恰好为菱形,则 PQ 的长为 .
【卷II】基础运算与基本技能
阅卷人
得分
三、解答题(共72分)
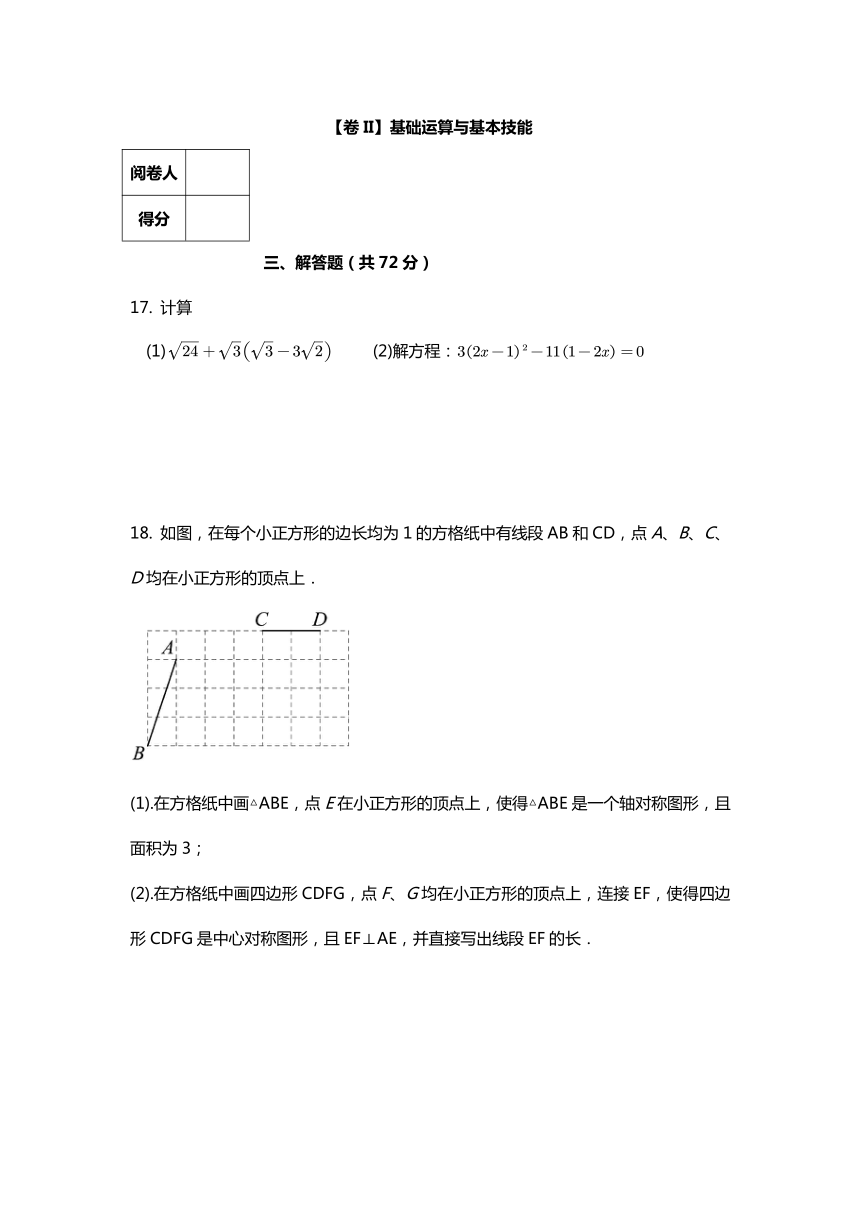
17. 计算
(1) (2)解方程:
18. 如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上.
(1).在方格纸中画△ABE,点E在小正方形的顶点上,使得△ABE是一个轴对称图形,且面积为3;
(2).在方格纸中画四边形CDFG,点F、G均在小正方形的顶点上,连接EF,使得四边形CDFG是中心对称图形,且EF⊥AE,并直接写出线段EF的长.
19. 2024年4月25日,神舟十八号载人飞船发射取得成功,将我国航天事业推向了新的高峰.南沙区某中学为了丰富学生们航天知识,组织全校学生进行航天知识竞赛,并随机抽取50名学生的成绩,整理成如下统计表:
分数 60 70 80 90 100
频数 2 3 15 16 14
(1).该50名同学这次竞赛成绩的中位数是________;
(2).求该50名同学这次竞赛成绩的平均数;
(3).若竞赛成绩90分以上(含90分)为优秀,该校有1500名学生,请估计竞赛成绩为优秀的人数.
20. 为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神,2024年10月21日至24日某市开展青少年机器人竞赛活动.某商家为本次比赛供应器材,因供过于求,还余20套器材需要进行零售.为了尽快减少库存,商家决定采取降价措施,原来每套器材的售价为100元,经过两次降价后每套器材的售价为81元,并且每次降价的百分率相同.
(1).求每次降价的百分率;
(2).若每套器材的进价为76元,通过以上两次降价的方式,将剩余的20套器材全部售出,并且确保两次降价销售的总利润不少于200元,那么第一降价至少售出多少套器材后方可进行第二次降价?
21. 如图1,△ABC的两条高AD与BE交于点O,AD=BD,
(1).若BE平分∠ABC,请求出∠BAC的度数;
(2).如图2,连接OC,请判断△ODC的形状,并说明理由;
(3).若AC=5,F是射线BC上一点,且CF=AO,动点P从点O出发,沿线段OB以每秒1个单位长度的速度向终点B运动,同时动点Q从点A出发,沿射线AC以每秒3个单位长度的速度运动,当点P到达点B时,P,Q两点同时停止运动,设运动时间为t秒,当△AOP与△FCQ全等时,请直接写出此时t的值.
22. 在四边形ABCD中,对角线AC, BD相交于点O.在线段AO上任取一点P(端点除外),连接PD,PB.点Q在BA的延长线上且PQ=PD.
(1).如图1,若四边形ABCD是正方形.
①求∠DPQ的度数;
②探究AQ与OP的数量关系并说明理由.
(2).如图2,若四边形ABCD是菱形且∠ABC=60°.探究AQ与CP的数量关系并说明理由.
参考答案
一、选择题
1. C . 2. C 3. B 4. A 5. C 6. C . 7. B .8. B 9. C 10. D
二、填空题
11.
12. 4
13. 11.3
14.
15. 60°
16. 2.8
三、解答题
17. (1) (2)
18.
(1)
(2)
19. (1). 90 (2). 87.4 (3). 估计竞赛成绩为优秀的人数为900人
20. (1)10%, (2)12套
21. (1)67.5° (2)△ODC是等腰直角三角形 (3)
22 (1). 90°; AQ=OP (2)AQ=CP
(浙江专用)
【5月】
测试范围:第1~5单元(浙教版 八年级下册)。
考试时间:120分钟 满分:120分
题号 一 二 三 总分
评分
注意事项:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分。答卷前,考生务必将自己的姓名、准考
证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
【卷I】基础知识与基本能力
阅卷人
得分
一、反复比较,合理选择(每题3分,共30分)
1. 下列交通标志中是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2. 估计的运算结果在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
3. 面试时,小王的基本知识、表达能力、工作态度的得分分别是89分、78分、85分,若依次按40%, 30%, 30%的比例确定面试成绩,则小王的面试成绩为( )
A. 82分 B. 84.5分 C. 85.5分 D. 85分
4. 下列命题是假命题的是( )
A.若|a|=|b|,则a=b
B.两直线平行,同位角相等
C.对顶角相等
D.若b2﹣4ac>0,则方程ax2+bx+c=0(a≠0)有两个不等的实数根
5. 如图放置的五块拼图中,①②③为正方形,④⑤为等腰直角三角形,若正方形③的面积为2,则正方形②的面积为( )
A.4 B.6 C.8 D.12
6. 将式子根式外的因式移到根式内的结果是( )
A. B. C. D.
7. 用一条长40cm的绳子怎样围成一个面积为75cm2的矩形?设矩形的一边为x米,根据题意,可列方程为( )
A.x(40-x)=75 B.x(20-x)=75 C.x(x+40)=75 D.x(x+20)=7
8. 某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛,而这9名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的( )
A.平均数 B.中位数 C.众数 D.方差
9. 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF交AD于点G.下列结论:
① AE=AF;
② ∠EAF + ∠EDF=180°;
③ EF垂直平分AD;
④四边形AEDF的面积为线段EF与AD乘积的一半;
其中结论正确的是( )
A.①②③ B.②③④ C.①②④ D.①②③④
10. 如图,在矩形ABCD中,∠BAD的平分线AE交BC于点E,且AD=AE,DH⊥AE于点H,连接BH并延长,交CD于点F,连接DE.下列结论:①;②∠AED=∠CED;③BH=HF;④BC=2HE+CF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
阅卷人
得分
二、用心思考,正确填写(每小题3分,共18分)
11. 若实数x,y满足y=-+3,则的值等于 .
12. 已知方程的两根分别为,则的值为 .
13. 某学校餐厅有10元、12元、15元三种盒饭供学生选择.某天盒饭的销售情况如图所示,则当天学生购买盒饭费用的平均数是 元.
14. 如图,平面直角坐标系中,已知直线,的边OC在x轴正半轴上,点B的坐标是(9,3),正以每秒1个单位长度的速度沿着x轴向左平移,经过____________秒,直线将分成面积相等的两部分.
15. 三个正方形的摆放位置如图所示,若∠1=30°,则∠2+∠3= .
16. 在矩形 ABCD 中,AB=4,AD=3,P,Q 是对角线 BD 上不重合的两点,点 P 关于直线 AD,AB 的对称点分别是点 E,F,点 Q 关于直线 BC,CD 的对称点分别是点 G,H.若由点 E,F,G,H 构成的四边形恰好为菱形,则 PQ 的长为 .
【卷II】基础运算与基本技能
阅卷人
得分
三、解答题(共72分)
17. 计算
(1) (2)解方程:
18. 如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上.
(1).在方格纸中画△ABE,点E在小正方形的顶点上,使得△ABE是一个轴对称图形,且面积为3;
(2).在方格纸中画四边形CDFG,点F、G均在小正方形的顶点上,连接EF,使得四边形CDFG是中心对称图形,且EF⊥AE,并直接写出线段EF的长.
19. 2024年4月25日,神舟十八号载人飞船发射取得成功,将我国航天事业推向了新的高峰.南沙区某中学为了丰富学生们航天知识,组织全校学生进行航天知识竞赛,并随机抽取50名学生的成绩,整理成如下统计表:
分数 60 70 80 90 100
频数 2 3 15 16 14
(1).该50名同学这次竞赛成绩的中位数是________;
(2).求该50名同学这次竞赛成绩的平均数;
(3).若竞赛成绩90分以上(含90分)为优秀,该校有1500名学生,请估计竞赛成绩为优秀的人数.
20. 为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神,2024年10月21日至24日某市开展青少年机器人竞赛活动.某商家为本次比赛供应器材,因供过于求,还余20套器材需要进行零售.为了尽快减少库存,商家决定采取降价措施,原来每套器材的售价为100元,经过两次降价后每套器材的售价为81元,并且每次降价的百分率相同.
(1).求每次降价的百分率;
(2).若每套器材的进价为76元,通过以上两次降价的方式,将剩余的20套器材全部售出,并且确保两次降价销售的总利润不少于200元,那么第一降价至少售出多少套器材后方可进行第二次降价?
21. 如图1,△ABC的两条高AD与BE交于点O,AD=BD,
(1).若BE平分∠ABC,请求出∠BAC的度数;
(2).如图2,连接OC,请判断△ODC的形状,并说明理由;
(3).若AC=5,F是射线BC上一点,且CF=AO,动点P从点O出发,沿线段OB以每秒1个单位长度的速度向终点B运动,同时动点Q从点A出发,沿射线AC以每秒3个单位长度的速度运动,当点P到达点B时,P,Q两点同时停止运动,设运动时间为t秒,当△AOP与△FCQ全等时,请直接写出此时t的值.
22. 在四边形ABCD中,对角线AC, BD相交于点O.在线段AO上任取一点P(端点除外),连接PD,PB.点Q在BA的延长线上且PQ=PD.
(1).如图1,若四边形ABCD是正方形.
①求∠DPQ的度数;
②探究AQ与OP的数量关系并说明理由.
(2).如图2,若四边形ABCD是菱形且∠ABC=60°.探究AQ与CP的数量关系并说明理由.
参考答案
一、选择题
1. C . 2. C 3. B 4. A 5. C 6. C . 7. B .8. B 9. C 10. D
二、填空题
11.
12. 4
13. 11.3
14.
15. 60°
16. 2.8
三、解答题
17. (1) (2)
18.
(1)
(2)
19. (1). 90 (2). 87.4 (3). 估计竞赛成绩为优秀的人数为900人
20. (1)10%, (2)12套
21. (1)67.5° (2)△ODC是等腰直角三角形 (3)
22 (1). 90°; AQ=OP (2)AQ=CP
同课章节目录
