浙教版2024—2025学年八年级下学期数学第三次月考全真模拟试卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下学期数学第三次月考全真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 508.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 17:38:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下学期数学第三次月考全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,中心对称图形是( )
A. B. C. D.
2.估计的值在( )
A.8到9之间 B.7到8之间 C.6到7之间 D.5到6之间
3.某校举办水浒文化进校园朗诵大赛,比赛中七位评委给某位参赛选手的分数,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A.中位数 B.众数 C.平均数 D.方差
4.某校竞选学生会主席分为现场演讲和答辩两个环节,其中现场演讲分占80%,答辩分占20%,小明参加并在这两个环节中分别取得85分和90分的成绩,则小明的最终成绩为( )
A.80分 B.84分 C.86分 D.88分
5.关于x的一元二次方程x2+mx﹣4=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
6.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠B,∠C=∠D B.AB=AD,CB=CD
C.AB=CD,AD=BC D.AB∥CD,AD=BC
7.公安部交管局部署“一盔一带”安全守护行动,某头盔经销商经统计发现某品牌头盔5月份销售量144个,7月份销售量225个,从5月份到7月份销售量的月增长率相同,则此月增长率为( )
A.83% B.69% C.25% D.20%
8.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,首先应假设这个直角三角形中( )
A.两个锐角都大于45°
B.两个锐角都小于45°
C.两个锐角都不大于45°
D.两个锐角都等于45°
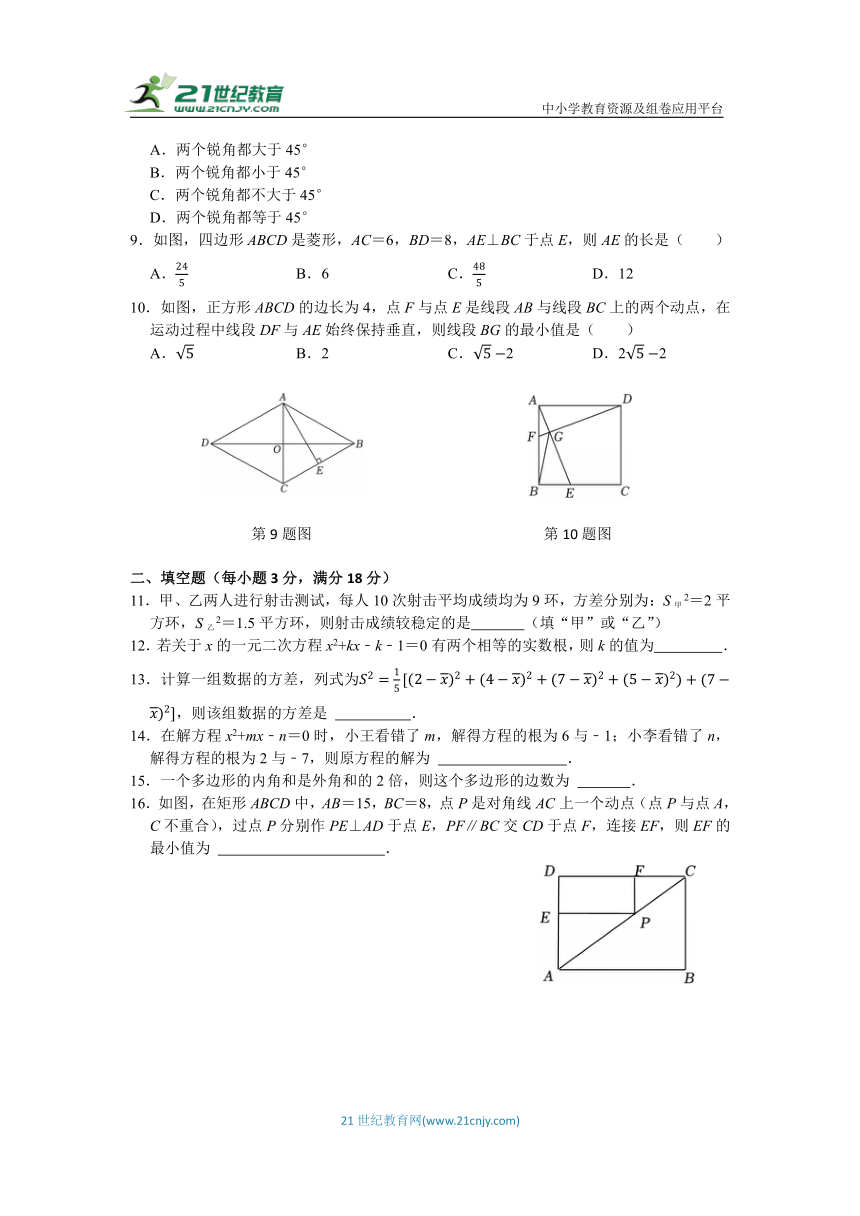
9.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
10.如图,正方形ABCD的边长为4,点F与点E是线段AB与线段BC上的两个动点,在运动过程中线段DF与AE始终保持垂直,则线段BG的最小值是( )
A. B.2 C.2 D.22
二、填空题(每小题3分,满分18分)
11.甲、乙两人进行射击测试,每人10次射击平均成绩均为9环,方差分别为:S甲2=2平方环,S乙2=1.5平方环,则射击成绩较稳定的是 (填“甲”或“乙”)
12.若关于x的一元二次方程x2+kx﹣k﹣1=0有两个相等的实数根,则k的值为 .
13.计算一组数据的方差,列式为,则该组数据的方差是 .
14.在解方程x2+mx﹣n=0时,小王看错了m,解得方程的根为6与﹣1;小李看错了n,解得方程的根为2与﹣7,则原方程的解为 .
15.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.如图,在矩形ABCD中,AB=15,BC=8,点P是对角线AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥AD于点E,PF∥BC交CD于点F,连接EF,则EF的最小值为 .
浙教版2024—2025学年八年级下学期数学第三次月考全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.按要求解下列问题:
(1)计算: (2)若,求代数式:的值.
18.解方程:
(1)x2﹣2x=15. (2)(x﹣1)(x+5)=﹣2(x+5).
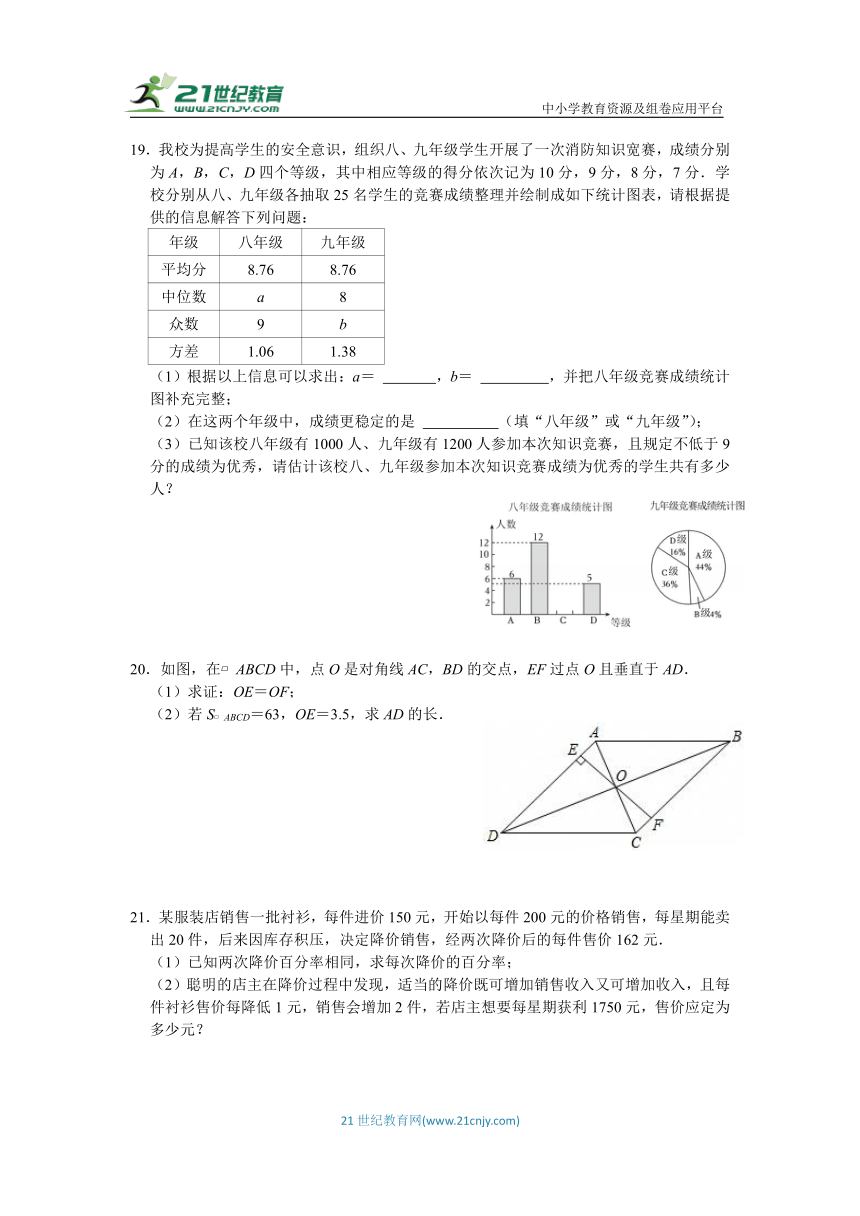
19.我校为提高学生的安全意识,组织八、九年级学生开展了一次消防知识宽赛,成绩分别为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分,8分,7分.学校分别从八、九年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:
年级 八年级 九年级
平均分 8.76 8.76
中位数 a 8
众数 9 b
方差 1.06 1.38
(1)根据以上信息可以求出:a= ,b= ,并把八年级竞赛成绩统计图补充完整;
(2)在这两个年级中,成绩更稳定的是 (填“八年级”或“九年级”);
(3)已知该校八年级有1000人、九年级有1200人参加本次知识竞赛,且规定不低于9分的成绩为优秀,请估计该校八、九年级参加本次知识竞赛成绩为优秀的学生共有多少人?
20.如图,在 ABCD中,点O是对角线AC,BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
21.某服装店销售一批衬衫,每件进价150元,开始以每件200元的价格销售,每星期能卖出20件,后来因库存积压,决定降价销售,经两次降价后的每件售价162元.
(1)已知两次降价百分率相同,求每次降价的百分率;
(2)聪明的店主在降价过程中发现,适当的降价既可增加销售收入又可增加收入,且每件衬衫售价每降低1元,销售会增加2件,若店主想要每星期获利1750元,售价应定为多少元?
22.阅读与思考
配方思想,是初中数学重要的思想方法之一,用配方思想方法,可以简化数学运算,常用的配方公式有:a2+b2=(a+b)2﹣2ab,a2+b2=(a﹣b)2+2ab.用配方思想方法,解答下面问题:
(1)已知:,求的值;
(2)已知:,,求3x2﹣2xy+3y2的值;
(3)已知:,,(a≥0,b≥0),求a+2b的值.
23.已知关于x的方程x2﹣(k+3)x+3k=0.
(1)求证:无论k取任何实数,该方程总有实数根;
(2)若等腰三角形的三边长分别为a,b,c,其中a=1,并且b,c恰好是此方程的两个实数根,求此三角形的周长.
24.如图1,在平行四边形ABCD中,∠ABC为钝角,BE,BF分别为边AD,CD上的高,交边AD,CD于点E,F,连结EF,BF=EF.
(1)求证:∠EBF=∠C;
(2)求证:CF=DF;
(3)如图2,若∠DBC=45°,以点B为原点建立平面直角坐标系,点C坐标为,点P为直线CE上一动点,当S△BCP=S△BDE时,求出此时点P的坐标.
25.如图,点E是正方形ABCD边BC上一动点(不与B、C重合),CM是外角∠DCN的平分线,点F在射线CM上.
(1)当∠CEF=∠BAE时,判断AE与EF是否垂直,并证明结论;
(2)若在点E运动过程中,线段CF与BE始终满足关系式CF=BE.
①连接AF,证明的值为常量;
②设AF与CD的交点为G,△CEG的周长为a,求正方形ABCD的面积.
参考答案
一、选择题
1—10:DCACACCAAD
二、填空题
11.【解答】解:∵S甲2=2>S乙2=1.5,方差小的为乙,
∴本题中成绩比较稳定的是乙.
故答案为:乙.
12.【解答】解:∵方程x2+kx﹣k﹣1=0有两个相等的实数根,
∴Δ=k2﹣4(﹣k﹣1)=k2+4k+4=(k+2)2=0,
解得:k=﹣2.
故答案为:﹣2.
13.【解答】解:由方差计算公式得这组数据为:2,4,7,5,7,
∴,
∴
=3.6;
故答案为:3.6.
14.【解答】解:根据根与系数关系得,
﹣n=6×(﹣1),﹣m=2﹣7,
解得:n=6,m=5,
∴原方程为x2+5x﹣6=0,
(x﹣1)(x+6)=0,
x﹣1=0或x+6=0,
∴x1=1,x2=﹣6,
故答案为:x1=1,x2=﹣6.
15.【解答】解:∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形的边数为6.
故答案为:6.
16.【解答】解:如图,过点D作DP′⊥AC于P′,连接EF,DP,
∵四边形ABCD是矩形,AB=15,BC=8,
∴CD=AB=15,AD=BC=8,∠ADC=90°,
∴,
∵PF∥BC,
∴∠PFD+∠ADC=180°,
∴∠PFD=90°,
∵PE⊥AD,
∴∠PED=∠EDF=∠PFD=90°,
∴四边形DEPF是矩形,
∴EF=DP,
要使EF最小,只需DP最小,当DP⊥AC时,DP最小,最小值为DP′的长,
∵,
∴,
故EF的最小值为,
故答案为:.
三、解答题
17.【解答】解:(1)
=2
;
(2)∵a1,
∴a>2,
则原式
=a﹣(a﹣2)
=2.
18.【解答】解:(1)x2﹣2x=15,
(x﹣5)(x+3)=0,
即:x﹣5=0或x+3=0,
∴x=5或x=﹣3.
(2)(x﹣1)(x+5)=﹣2(x+5),
(x﹣1)(x+5)+2(x+5)=0,
(x﹣1+2)(x+5)=0,
即:x+1=0或x+5=0,
∴x=﹣1或x=﹣5.
19.【解答】解:(1)由条件可知:八年级中位数为从小到大排序后的第13名同学的成绩,
由条形统计图可知;从小到大排序后的第13名同学的成绩在等级B中,
故八年级中位数a=9,
由扇形图可知:44%>36%>16%>4%即等级A所占比例最多,
∴九年级众数b=10,
由题可知:八年级等级C人数为:25﹣6﹣12﹣5=2(人),
补全条形统计图如下:
故答案为:9,10;
(2)∵八、九年级平均分相同,而八年级中位数大于九年级中位数,八年级方差小于九年级方差,
∴八年级成绩更好,更稳定;
故答案为:八年级;
(3)八年级优秀人数为人.
九年级优秀人数为1200×(44%+4%)=576人.
∴两个年级优秀学生总人数为720+576=1296人.
20.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AEO≌△CFO,(ASA)
∴OE=OF;
(2)解:∵OE=OF,OE=3.5,
∴EF=2OE=7,
又∵EF⊥AD,
∴S ABCD=AD×EF=63,
∴AD=9.
21.【解答】解:(1)设每次降价的百分率为x,
依题意得:200(1﹣x)2=162,
解得:x1=0.1=10%,x2=1.9(不符合题意,舍去),
答:每次降价的百分率为10%;
(2)设售价应定为y元,则每件的销售利润为(y﹣150)元,每星期可卖出20+(200﹣y)×2=(420﹣2y)(件),
依题意得:(y﹣150)(420﹣2y)=1750,
整理得:y2﹣360y+32375=0,
解得:y1=175,y2=185(不符合题意,舍去).
答:售价应定为175元.
22.【解答】解:(1)由条件可知;
(2),
,
,
,
原式=3[(x+y)2﹣2xy]﹣2xy
=3(x+y)2﹣8xy
=3×122﹣8×1
=424;
(3)∵,,
∴.
23.【解答】(1)证明:∵关于x的方程x2﹣(k+3)x+3k=0,
∴Δ=[﹣(k+3)]2﹣12k
=k2+6k+9﹣12k
=k2﹣6k+9
=(k﹣3)2≥0,
则无论k取何实数值,方程总有实数根;
(2)解:当b=c时,k=3,方程为x2﹣6x+9=0,
解得:x1=x2=3,
此时三边长为1,3,3,周长为1+3+3=7;
当a=b=1或a=c=1时,把x=1代入方程得:1﹣(k+3)+3k=0,
解得:k=1,此时方程为:x2﹣4x+3=0,
解得:x1=3,x2=1,
当x'=1时,
此时三边长为1,1,3,不能组成三角形,
当x=3时,此时三边长为1,3,3,周长为3+3+1=7,
综上所述,△ABC的周长为7.
24.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵BE,BF分别为边AD,CD上的高,
∴AD⊥BE,∠BFC=90°,
∴BE⊥BC,
∴∠EBC=90°=∠BFC,
∴∠EBF+∠CBF=90°=∠C+∠CBF,
∴∠EBF=∠C;
(2)证明:如图2,延长EF,BC交于点H,
∵BF=EF,
∴∠FEB=∠FBE,
∵∠EBC=90°,
∴∠FBH=∠FHB,
∴BF=FH,
∴EF=FH,
∵AD∥BC,
∴∠ADC=∠DCH,
在△EDF和△HCF中,
,
∴△EDF≌△HCF(AAS),
∴DF=CF;
(3)解:分两种情况:
①如图3,点P在x轴的上方,过点P作PG⊥x轴于G,
∵点C坐标为,
∴BC,
∵BF⊥CD,DF=CF,
∴BD=BC,
∵AD∥BC,
∴∠ADB=∠DBC=45°,
∴△BED是等腰直角三角形,
∴BE=DE=1,
∴S△BED1×1,
∵S△BCP=S△BDE,
∴ PG,
∴PG,
∵E(0,1),C(,0),
设直线CE的解析式为:y=kx+b,
∴,
解得:,
∴直线CE的解析式为:yx+1,
当y时,x+1,
∴x1,
∴点P的坐标为(1,);
如图4,P在x轴的下方,过点P作PG⊥x轴于G,
由①可知:PG,直线CE的解析式为:yx+1,
当y时,x+1,
∴x1,
∴点P的坐标为(1,);
综上,点P的坐标为(1,)或(1,).
25.【解答】(1)解:垂直,理由如下:
∵四边形ABCD是正方形,
∴∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠CEF=∠BAE,
∴∠CEF+∠AEB=90°,
∴∠AEF=90°,
∴AE⊥EF;
(2)①证明:如图1,
作FG⊥BN于G,
∵四边形ABCD是正方形,
∴∠DCN=∠BCD=90°,AB=BC,
∵CMP平分∠DCN,
∴∠DCM=∠MCN=45°,
∴CF=,
∵CF=,
∴BE=CG=CF,
∴BE+EC=CG+EC,
∴BC=EG,
∴EG=AB,
∵∠FCG=∠B=90°,
∴△ABE≌△EGF(SAS),
∴AE=EF,∠FEG=∠BAE,
∴由(1)得:∠AEF=90°,
∴=;
②解:如图2,
在CB的延长线上截取BH=DG,连接AH,
∵四边形ABCD是正方形,
∴∠ABH=∠ABC=∠BAD=∠D=90°,AB=AD=BC=CD,
∴△ABH≌△ADG(SAS),
∴∠DAG=∠BAH,AH=AG,
由①知:∠EAF=45°,
∴∠BAE+∠DAG=45°,
∴∠BAE+∠BAH=45°,
∴∠EAH=45°,
∴∠EAH=∠EAF,
∵AE=AE,
∴△AEH≌△AEG,
∴EG=EH=BH+BE=DG+BE,
∴EG+CG+EC=DG+BE+CG+EC=CD+BC=2BC=a,
∴BC=,
∴S正方形ABCD=BC2=.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下学期数学第三次月考全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,中心对称图形是( )
A. B. C. D.
2.估计的值在( )
A.8到9之间 B.7到8之间 C.6到7之间 D.5到6之间
3.某校举办水浒文化进校园朗诵大赛,比赛中七位评委给某位参赛选手的分数,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A.中位数 B.众数 C.平均数 D.方差
4.某校竞选学生会主席分为现场演讲和答辩两个环节,其中现场演讲分占80%,答辩分占20%,小明参加并在这两个环节中分别取得85分和90分的成绩,则小明的最终成绩为( )
A.80分 B.84分 C.86分 D.88分
5.关于x的一元二次方程x2+mx﹣4=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
6.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠B,∠C=∠D B.AB=AD,CB=CD
C.AB=CD,AD=BC D.AB∥CD,AD=BC
7.公安部交管局部署“一盔一带”安全守护行动,某头盔经销商经统计发现某品牌头盔5月份销售量144个,7月份销售量225个,从5月份到7月份销售量的月增长率相同,则此月增长率为( )
A.83% B.69% C.25% D.20%
8.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,首先应假设这个直角三角形中( )
A.两个锐角都大于45°
B.两个锐角都小于45°
C.两个锐角都不大于45°
D.两个锐角都等于45°
9.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
10.如图,正方形ABCD的边长为4,点F与点E是线段AB与线段BC上的两个动点,在运动过程中线段DF与AE始终保持垂直,则线段BG的最小值是( )
A. B.2 C.2 D.22
二、填空题(每小题3分,满分18分)
11.甲、乙两人进行射击测试,每人10次射击平均成绩均为9环,方差分别为:S甲2=2平方环,S乙2=1.5平方环,则射击成绩较稳定的是 (填“甲”或“乙”)
12.若关于x的一元二次方程x2+kx﹣k﹣1=0有两个相等的实数根,则k的值为 .
13.计算一组数据的方差,列式为,则该组数据的方差是 .
14.在解方程x2+mx﹣n=0时,小王看错了m,解得方程的根为6与﹣1;小李看错了n,解得方程的根为2与﹣7,则原方程的解为 .
15.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
16.如图,在矩形ABCD中,AB=15,BC=8,点P是对角线AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥AD于点E,PF∥BC交CD于点F,连接EF,则EF的最小值为 .
浙教版2024—2025学年八年级下学期数学第三次月考全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.按要求解下列问题:
(1)计算: (2)若,求代数式:的值.
18.解方程:
(1)x2﹣2x=15. (2)(x﹣1)(x+5)=﹣2(x+5).
19.我校为提高学生的安全意识,组织八、九年级学生开展了一次消防知识宽赛,成绩分别为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分,8分,7分.学校分别从八、九年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:
年级 八年级 九年级
平均分 8.76 8.76
中位数 a 8
众数 9 b
方差 1.06 1.38
(1)根据以上信息可以求出:a= ,b= ,并把八年级竞赛成绩统计图补充完整;
(2)在这两个年级中,成绩更稳定的是 (填“八年级”或“九年级”);
(3)已知该校八年级有1000人、九年级有1200人参加本次知识竞赛,且规定不低于9分的成绩为优秀,请估计该校八、九年级参加本次知识竞赛成绩为优秀的学生共有多少人?
20.如图,在 ABCD中,点O是对角线AC,BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
21.某服装店销售一批衬衫,每件进价150元,开始以每件200元的价格销售,每星期能卖出20件,后来因库存积压,决定降价销售,经两次降价后的每件售价162元.
(1)已知两次降价百分率相同,求每次降价的百分率;
(2)聪明的店主在降价过程中发现,适当的降价既可增加销售收入又可增加收入,且每件衬衫售价每降低1元,销售会增加2件,若店主想要每星期获利1750元,售价应定为多少元?
22.阅读与思考
配方思想,是初中数学重要的思想方法之一,用配方思想方法,可以简化数学运算,常用的配方公式有:a2+b2=(a+b)2﹣2ab,a2+b2=(a﹣b)2+2ab.用配方思想方法,解答下面问题:
(1)已知:,求的值;
(2)已知:,,求3x2﹣2xy+3y2的值;
(3)已知:,,(a≥0,b≥0),求a+2b的值.
23.已知关于x的方程x2﹣(k+3)x+3k=0.
(1)求证:无论k取任何实数,该方程总有实数根;
(2)若等腰三角形的三边长分别为a,b,c,其中a=1,并且b,c恰好是此方程的两个实数根,求此三角形的周长.
24.如图1,在平行四边形ABCD中,∠ABC为钝角,BE,BF分别为边AD,CD上的高,交边AD,CD于点E,F,连结EF,BF=EF.
(1)求证:∠EBF=∠C;
(2)求证:CF=DF;
(3)如图2,若∠DBC=45°,以点B为原点建立平面直角坐标系,点C坐标为,点P为直线CE上一动点,当S△BCP=S△BDE时,求出此时点P的坐标.
25.如图,点E是正方形ABCD边BC上一动点(不与B、C重合),CM是外角∠DCN的平分线,点F在射线CM上.
(1)当∠CEF=∠BAE时,判断AE与EF是否垂直,并证明结论;
(2)若在点E运动过程中,线段CF与BE始终满足关系式CF=BE.
①连接AF,证明的值为常量;
②设AF与CD的交点为G,△CEG的周长为a,求正方形ABCD的面积.
参考答案
一、选择题
1—10:DCACACCAAD
二、填空题
11.【解答】解:∵S甲2=2>S乙2=1.5,方差小的为乙,
∴本题中成绩比较稳定的是乙.
故答案为:乙.
12.【解答】解:∵方程x2+kx﹣k﹣1=0有两个相等的实数根,
∴Δ=k2﹣4(﹣k﹣1)=k2+4k+4=(k+2)2=0,
解得:k=﹣2.
故答案为:﹣2.
13.【解答】解:由方差计算公式得这组数据为:2,4,7,5,7,
∴,
∴
=3.6;
故答案为:3.6.
14.【解答】解:根据根与系数关系得,
﹣n=6×(﹣1),﹣m=2﹣7,
解得:n=6,m=5,
∴原方程为x2+5x﹣6=0,
(x﹣1)(x+6)=0,
x﹣1=0或x+6=0,
∴x1=1,x2=﹣6,
故答案为:x1=1,x2=﹣6.
15.【解答】解:∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形的边数为6.
故答案为:6.
16.【解答】解:如图,过点D作DP′⊥AC于P′,连接EF,DP,
∵四边形ABCD是矩形,AB=15,BC=8,
∴CD=AB=15,AD=BC=8,∠ADC=90°,
∴,
∵PF∥BC,
∴∠PFD+∠ADC=180°,
∴∠PFD=90°,
∵PE⊥AD,
∴∠PED=∠EDF=∠PFD=90°,
∴四边形DEPF是矩形,
∴EF=DP,
要使EF最小,只需DP最小,当DP⊥AC时,DP最小,最小值为DP′的长,
∵,
∴,
故EF的最小值为,
故答案为:.
三、解答题
17.【解答】解:(1)
=2
;
(2)∵a1,
∴a>2,
则原式
=a﹣(a﹣2)
=2.
18.【解答】解:(1)x2﹣2x=15,
(x﹣5)(x+3)=0,
即:x﹣5=0或x+3=0,
∴x=5或x=﹣3.
(2)(x﹣1)(x+5)=﹣2(x+5),
(x﹣1)(x+5)+2(x+5)=0,
(x﹣1+2)(x+5)=0,
即:x+1=0或x+5=0,
∴x=﹣1或x=﹣5.
19.【解答】解:(1)由条件可知:八年级中位数为从小到大排序后的第13名同学的成绩,
由条形统计图可知;从小到大排序后的第13名同学的成绩在等级B中,
故八年级中位数a=9,
由扇形图可知:44%>36%>16%>4%即等级A所占比例最多,
∴九年级众数b=10,
由题可知:八年级等级C人数为:25﹣6﹣12﹣5=2(人),
补全条形统计图如下:
故答案为:9,10;
(2)∵八、九年级平均分相同,而八年级中位数大于九年级中位数,八年级方差小于九年级方差,
∴八年级成绩更好,更稳定;
故答案为:八年级;
(3)八年级优秀人数为人.
九年级优秀人数为1200×(44%+4%)=576人.
∴两个年级优秀学生总人数为720+576=1296人.
20.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AEO≌△CFO,(ASA)
∴OE=OF;
(2)解:∵OE=OF,OE=3.5,
∴EF=2OE=7,
又∵EF⊥AD,
∴S ABCD=AD×EF=63,
∴AD=9.
21.【解答】解:(1)设每次降价的百分率为x,
依题意得:200(1﹣x)2=162,
解得:x1=0.1=10%,x2=1.9(不符合题意,舍去),
答:每次降价的百分率为10%;
(2)设售价应定为y元,则每件的销售利润为(y﹣150)元,每星期可卖出20+(200﹣y)×2=(420﹣2y)(件),
依题意得:(y﹣150)(420﹣2y)=1750,
整理得:y2﹣360y+32375=0,
解得:y1=175,y2=185(不符合题意,舍去).
答:售价应定为175元.
22.【解答】解:(1)由条件可知;
(2),
,
,
,
原式=3[(x+y)2﹣2xy]﹣2xy
=3(x+y)2﹣8xy
=3×122﹣8×1
=424;
(3)∵,,
∴.
23.【解答】(1)证明:∵关于x的方程x2﹣(k+3)x+3k=0,
∴Δ=[﹣(k+3)]2﹣12k
=k2+6k+9﹣12k
=k2﹣6k+9
=(k﹣3)2≥0,
则无论k取何实数值,方程总有实数根;
(2)解:当b=c时,k=3,方程为x2﹣6x+9=0,
解得:x1=x2=3,
此时三边长为1,3,3,周长为1+3+3=7;
当a=b=1或a=c=1时,把x=1代入方程得:1﹣(k+3)+3k=0,
解得:k=1,此时方程为:x2﹣4x+3=0,
解得:x1=3,x2=1,
当x'=1时,
此时三边长为1,1,3,不能组成三角形,
当x=3时,此时三边长为1,3,3,周长为3+3+1=7,
综上所述,△ABC的周长为7.
24.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵BE,BF分别为边AD,CD上的高,
∴AD⊥BE,∠BFC=90°,
∴BE⊥BC,
∴∠EBC=90°=∠BFC,
∴∠EBF+∠CBF=90°=∠C+∠CBF,
∴∠EBF=∠C;
(2)证明:如图2,延长EF,BC交于点H,
∵BF=EF,
∴∠FEB=∠FBE,
∵∠EBC=90°,
∴∠FBH=∠FHB,
∴BF=FH,
∴EF=FH,
∵AD∥BC,
∴∠ADC=∠DCH,
在△EDF和△HCF中,
,
∴△EDF≌△HCF(AAS),
∴DF=CF;
(3)解:分两种情况:
①如图3,点P在x轴的上方,过点P作PG⊥x轴于G,
∵点C坐标为,
∴BC,
∵BF⊥CD,DF=CF,
∴BD=BC,
∵AD∥BC,
∴∠ADB=∠DBC=45°,
∴△BED是等腰直角三角形,
∴BE=DE=1,
∴S△BED1×1,
∵S△BCP=S△BDE,
∴ PG,
∴PG,
∵E(0,1),C(,0),
设直线CE的解析式为:y=kx+b,
∴,
解得:,
∴直线CE的解析式为:yx+1,
当y时,x+1,
∴x1,
∴点P的坐标为(1,);
如图4,P在x轴的下方,过点P作PG⊥x轴于G,
由①可知:PG,直线CE的解析式为:yx+1,
当y时,x+1,
∴x1,
∴点P的坐标为(1,);
综上,点P的坐标为(1,)或(1,).
25.【解答】(1)解:垂直,理由如下:
∵四边形ABCD是正方形,
∴∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠CEF=∠BAE,
∴∠CEF+∠AEB=90°,
∴∠AEF=90°,
∴AE⊥EF;
(2)①证明:如图1,
作FG⊥BN于G,
∵四边形ABCD是正方形,
∴∠DCN=∠BCD=90°,AB=BC,
∵CMP平分∠DCN,
∴∠DCM=∠MCN=45°,
∴CF=,
∵CF=,
∴BE=CG=CF,
∴BE+EC=CG+EC,
∴BC=EG,
∴EG=AB,
∵∠FCG=∠B=90°,
∴△ABE≌△EGF(SAS),
∴AE=EF,∠FEG=∠BAE,
∴由(1)得:∠AEF=90°,
∴=;
②解:如图2,
在CB的延长线上截取BH=DG,连接AH,
∵四边形ABCD是正方形,
∴∠ABH=∠ABC=∠BAD=∠D=90°,AB=AD=BC=CD,
∴△ABH≌△ADG(SAS),
∴∠DAG=∠BAH,AH=AG,
由①知:∠EAF=45°,
∴∠BAE+∠DAG=45°,
∴∠BAE+∠BAH=45°,
∴∠EAH=45°,
∴∠EAH=∠EAF,
∵AE=AE,
∴△AEH≌△AEG,
∴EG=EH=BH+BE=DG+BE,
∴EG+CG+EC=DG+BE+CG+EC=CD+BC=2BC=a,
∴BC=,
∴S正方形ABCD=BC2=.
21世纪教育网(www.21cnjy.com)
同课章节目录
