浙教版2024—2025学年八年级下学期数学第三次月考模拟试卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年八年级下学期数学第三次月考模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 644.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 17:15:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年八年级下学期数学第三次月考模拟试卷
满分:120分 时间:120分钟 范围:第一章二次根式到第五章特殊平行四边形
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.二次根式中x的取值范围是( )
A.x=2 B.x≥2 C.x>2 D.x<2
2.用反证法证明命题“一个多边形最多有四个内角是直角”时,我们可以先假设( )
A.有三个直角
B.有四个直角
C.至少有四个内角是直角
D.至少有五个内角是直角
3.已知实数a,b在数轴上的位置如图所示,化简的正确结果是( )
A.a+b﹣1 B.1﹣a﹣b C.a﹣b+3 D.b﹣a﹣3
4.下列图标中,是中心对称图形的是( )
A. B. C. D.
5.以下说法正确的是( )
A.菱形的对角线互相垂直且相等
B.矩形的对角线互相平分且互相垂直
C.正方形的对角线互相垂直且平分
D.平行四边形的对角线互相平分且相等
6.如图,在直角坐标系中,菱形OABC的顶点C(3,4),反比例函数图象交线段AB,射线BC于点E,F,连接EF,则S△BEF的值是( )
A.6 B.7 C.8 D.9
7.已知正比例函数y1=﹣2x与反比例函数.对于实数m,当x=m时,y1>y2;当x=m+1时,y1<y2,则m的取值范围为( )
A.m<﹣2或0<m<2 B.﹣2<m<2
C.﹣3<m<﹣2或1<m<2 D.﹣2<m<0或m>2
8.如图,在矩形ABCD中,M是矩形内一点,设△ABM,△ADM,△CDM,△BCM的面积分别表示S1,S2,S3,S4,要求出S3﹣S4的值,只需知道( )
A.S4﹣S1 B.S2﹣S1 C.S3+S2 D.S3﹣S2
9.若一元二次方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围是( )
A.k>1 B.k<1 C.k<1且k≠0 D.k≥1
10.如图,矩形ABCD中,AB=3,AD=5,E,F分别是边AD,BC的中点,CP⊥BE于P,DP的延长线交AB于G.下列结论:①PF=2.5;②PF⊥DG;③.其中结论正确的有( )
A.①② B.②③ C.①③ D.①②③
二、填空题(每小题3分,满分18分)
11.甲、乙两人进行射击测试,每人10次射击平均成绩均为9环,方差分别为:S甲2=2平方环,S乙2=1.5平方环,则射击成绩较稳定的是 (填“甲”或“乙”)
12.若关于x的一元二次方程x2+kx﹣k﹣1=0有两个相等的实数根,则k的值为 .
13.计算一组数据的方差,列式为,则该组数据的方差是 .
14.二次根式在实数范围内有意义,则x的取值范围为 .
15.已知方程3x2+kx﹣2=0的一个根为2,则另一个根为 .
16.如图,已知菱形ABCD的面积为,,点P,Q分别是在边BC,CD上(不与C点重合),且CP=CQ,连结DP,AQ,则DP+AQ的最小值为 .
浙教版2024—2025学年八年级下学期数学第三次月考模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.(1)解方程:x(x﹣2)=x﹣2;(2)解方程:(3x﹣4)2=(4x﹣3)2.
18.(1)计算:;(2)计算:.
19.已知关于x的方程x2﹣(m+5)x+3m=0.
(1)求证:无论m取何值,此方程一定有实数根;
(2)若方程有一个实数根是5,求方程的另一个根.
20.如图,在菱形ABCD中,点P是BC边上的点,连结AP交对角线BD于点E,连结EC.
(1)求证:AE=CE.
(2)若∠ABC=45°,AE=PC,求∠BAP的度数.
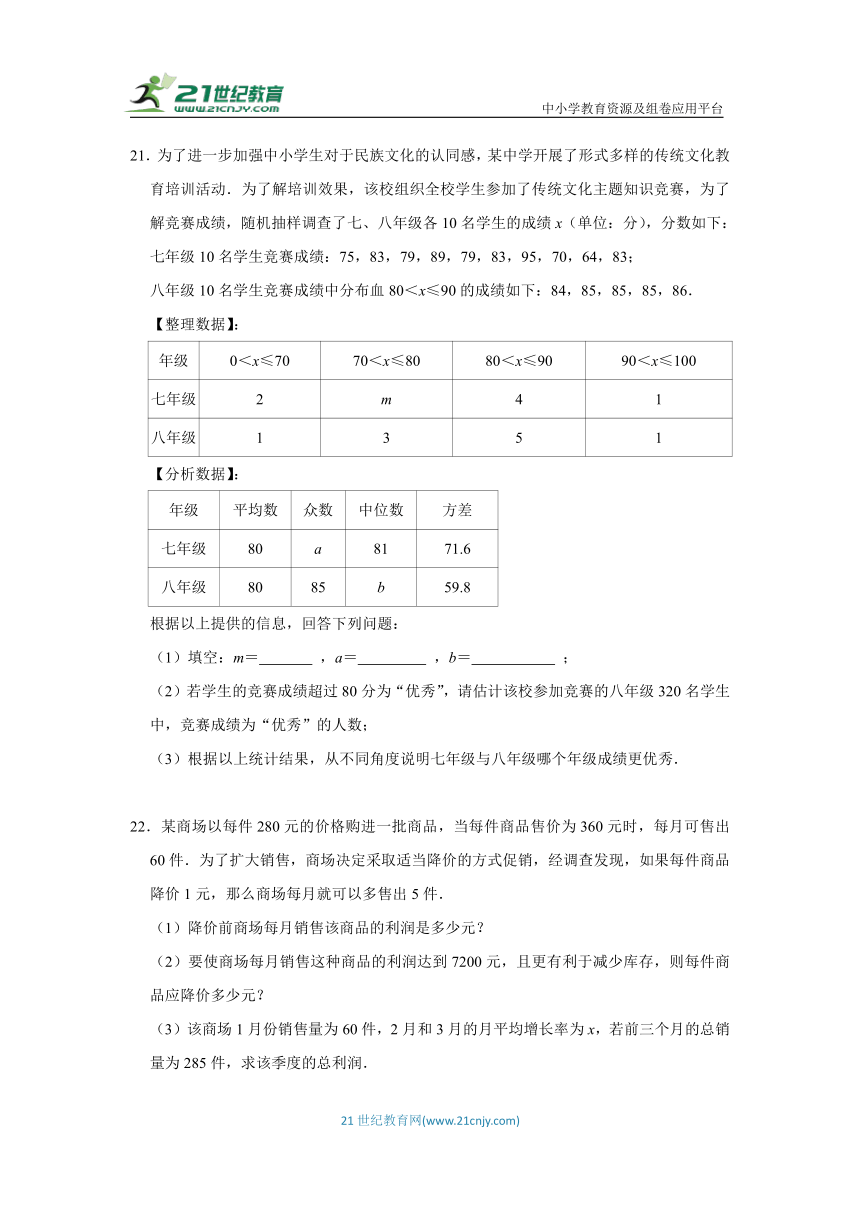
21.为了进一步加强中小学生对于民族文化的认同感,某中学开展了形式多样的传统文化教育培训活动.为了解培训效果,该校组织全校学生参加了传统文化主题知识竞赛,为了解竞赛成绩,随机抽样调查了七、八年级各10名学生的成绩x(单位:分),分数如下:
七年级10名学生竞赛成绩:75,83,79,89,79,83,95,70,64,83;
八年级10名学生竞赛成绩中分布血80<x≤90的成绩如下:84,85,85,85,86.
【整理数据】:
年级 0<x≤70 70<x≤80 80<x≤90 90<x≤100
七年级 2 m 4 1
八年级 1 3 5 1
【分析数据】:
年级 平均数 众数 中位数 方差
七年级 80 a 81 71.6
八年级 80 85 b 59.8
根据以上提供的信息,回答下列问题:
(1)填空:m= ,a= ,b= ;
(2)若学生的竞赛成绩超过80分为“优秀”,请估计该校参加竞赛的八年级320名学生中,竞赛成绩为“优秀”的人数;
(3)根据以上统计结果,从不同角度说明七年级与八年级哪个年级成绩更优秀.
22.某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件.为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.
(1)降价前商场每月销售该商品的利润是多少元?
(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
(3)该商场1月份销售量为60件,2月和3月的月平均增长率为x,若前三个月的总销量为285件,求该季度的总利润.
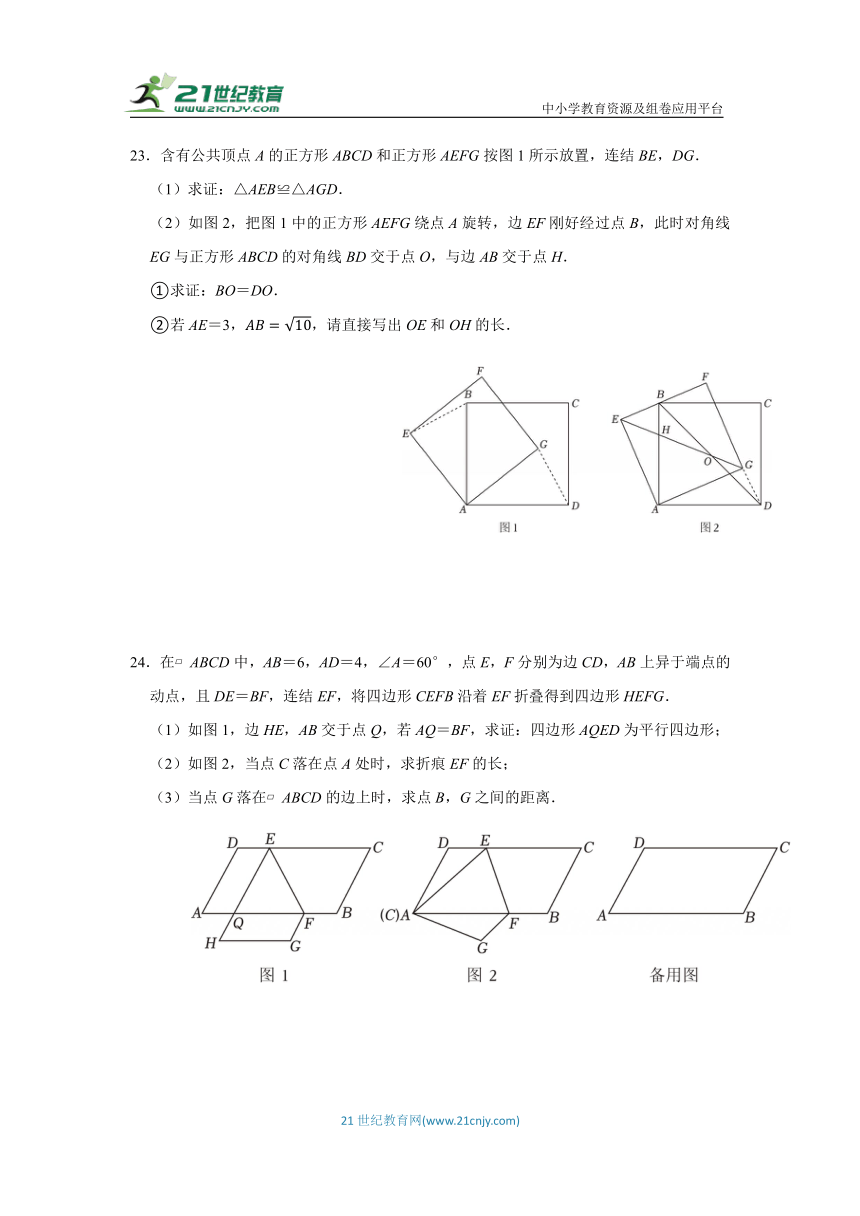
23.含有公共顶点A的正方形ABCD和正方形AEFG按图1所示放置,连结BE,DG.
(1)求证:△AEB≌△AGD.
(2)如图2,把图1中的正方形AEFG绕点A旋转,边EF刚好经过点B,此时对角线EG与正方形ABCD的对角线BD交于点O,与边AB交于点H.
①求证:BO=DO.
②若AE=3,,请直接写出OE和OH的长.
24.在 ABCD中,AB=6,AD=4,∠A=60°,点E,F分别为边CD,AB上异于端点的动点,且DE=BF,连结EF,将四边形CEFB沿着EF折叠得到四边形HEFG.
(1)如图1,边HE,AB交于点Q,若AQ=BF,求证:四边形AQED为平行四边形;
(2)如图2,当点C落在点A处时,求折痕EF的长;
(3)当点G落在 ABCD的边上时,求点B,G之间的距离.
25.关于x的一元二次方程x2+mx﹣1=0,当m=1时,该方程的正根称为黄金分割数.宽与长的比是黄金分割数的矩形叫做黄金矩形,希腊的巴特农神庙采用的就是黄金矩形的设计;我国著名数学家华罗庚的优选法中也应用到了黄金分割数.
(1)求黄金分割数;
(2)已知实数a,b满足a2+ma=1,b2﹣2mb=4,且b≠﹣2a,请证明:a,是一元二次方程x2+mx﹣1=0的两个根;
(3)已知两个不相等的实数p,q满足p2+np﹣1=q,q2+nq﹣1=p,求pq﹣n的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C B C C C B B D
1.【解答】解:由题意可得:x﹣2≥0,
解得:x≥2,
故选:B.
2.【解答】解:用反证法证明命题“一个多边形最多有四个内角是直角”时,首先应该假设至少有五个内角是直角,
故选:D.
3.【解答】解:由实数a,b在数轴上的位置可知,﹣1<a<0<1<b<2,
∴a+1>0,b﹣2<0,
∴原式=|a+1|+|b﹣2|
=a+1﹣b+2
=a﹣b+3.
故选:C.
4.【解答】解:选项A、C、D的图形都不能找到某一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形;
选项B的图形能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形;
故选:B.
5.【解答】解:A、菱形的对角线互相垂直且互相平分,故原选项错误,不符合题意;
B、矩形的对角线互相平分且相等,故原选项错误,不符合题意;
C、正方形的对角线互相垂直且平分,故原选项正确,符合题意;
D、平行四边形的对角线互相平分,故原选项错误,不符合题意.
故选:C.
6.【解答】解:∵C(3,4),
∴OC=BC5,
∴B(8,4),
在反比例函数y中,当y=4时,x=2,
F(2,4),
BF=8﹣2=6.
设直线AB的解析式为y=kx+b,A(5,0)、B(8,4)在直线上,
,解得,
∴直线AB的解析式为yx,
联立方程组,解得,,
∴E(6,),
∴S△BEF8.
故选:C.
7.【解答】解:联立方程组,解得或,
列函数的交点坐标为(2,﹣4),(﹣2,4),
∵当x=m时,y1>y2;
∴m<﹣2,或0<m<2,
∵当x=m+1时,y1<y2,
∴﹣2<m+1<0或m+1>2,
解得:﹣3<m<﹣1,或m>1.
∴﹣3<m<﹣2或1<m<2.
故选:C.
8.【解答】解:如图所示:连接MC,分别过点M作ME⊥AB交AB于点E,MF⊥AD交AD于点F,延长EM交CD于点G,延长FM交BC于点H,
∴∠AEM=∠MGD=90°,∠AFM=∠BHM=90°,
∵四边形ABCD是矩形,
∴∠BAD=∠ADC=∠ABC=∠BCD=90°,
∴四边形AEFM、BHME、MHCG和FMGD都是矩形,
∴AE=MF,BE=MH,EM=AF,MG=DF,
∴MF+MH=AE+BE=AB,EM+MG=AF+DF=AD,
∵△ABM的面积S1,△ADM的面积,△CDM的面积,△BCM的面积,
∴
,
S2+S4
,
∴S1+S3=S2+S4,
∴S3﹣S4=S2﹣S1,
∴要求出S3﹣S4的值,只需知道S2﹣S1,
故选:B.
9【解答】解:由题意知,Δ=4﹣4k>0,
解得:k<1.
故选:B.
10.【解答】解:连接GF,由矩形ABCD中,AB=3,AD=5,E,F分别是边AD,BC的中点,CP⊥BE于P,
得PF=BF=CF=2.5,故①对;
由DEADBC=BF,DE∥BF,
得四边形BEDF是平行四边形,
得BE∥DF,
得CP⊥DF,
由PF=CF,
得CP垂直平分DF,
得PD=CD=3,
得△DPF≌△DCF(SSS),
得∠DPF=∠DCF=90°,即PF⊥DG,故②对;
由∠GPF=∠GBF=90°,PF=BF,GF=GF,
得△GPF≌△GBF(HL),
得BG=PG=x,
由AG2+AD2=GD2,
得(3﹣x)2+52=(3+x)2,
得PG=x,故③对.
故选:D.
二、填空题
11.【解答】解:∵S甲2=2>S乙2=1.5,方差小的为乙,
∴本题中成绩比较稳定的是乙.
故答案为:乙.
12.【解答】解:∵方程x2+kx﹣k﹣1=0有两个相等的实数根,
∴Δ=k2﹣4(﹣k﹣1)=k2+4k+4=(k+2)2=0,
解得:k=﹣2.
故答案为:﹣2.
13.【解答】解:由方差计算公式得这组数据为:2,4,7,5,7,
∴,
∴
=3.6;
故答案为:3.6.
14.【解答】解:∵二次根式在实数范围内有意义,
∴x+2≥0,解得x≥﹣2.
故答案为:x≥﹣2.
15.【解答】解:令方程的另一个根为m,
则2m,
所以m,
即方程的另一个根为.
故答案为:.
16.【解答】解:如图,过点A作AM⊥BC于点M,延长AM到点A′,使A′M=AM,
∵四边形ABCD是菱形,
∴AB=BC=AD,∠ABC=∠ADC,
∵菱形ABCD的面积为,,
∴AM=2,
在Rt△ABM中,根据勾股定理得:
BM1,
以点B为原点,BC为x轴,垂直于BC方向为y轴,建立平面直角坐标系,
∴B(0,0),A(1,2),C(,0),D(1,2),A′(1,﹣2),
∵PC=CQ,BC=CD,
∴BP=DQ,
在△ABP和△ADQ中,
,
∴△ABP≌△ADQ(SAS),
∴AP=AQ=A′P,
连接A′D,AP,A′P,
∵A′P+PD>A′D,
∴A′,P,D三点共线时,PD+A′P取最小值,
∴PD+AQ的最小值=PD+A′P的最小值=A′D.
故答案为:.
三、解答题
17.【解答】解:(1)x(x﹣2)=x﹣2,
x(x﹣2)﹣(x﹣2)=0,
(x﹣2)(x﹣1)=0,
则x﹣2=0或x﹣1=0,
所以x1=2,x2=1.
(2)(3x﹣4)2=(4x﹣3)2,
(3x﹣4)2﹣(4x﹣3)2=0,
(3x﹣4+4x﹣3)(3x﹣4﹣4x+3)=0,
(7x﹣7)(﹣x﹣1)=0,
则7x﹣7=0或﹣x﹣1=0,
所以x1=1,x2=﹣1.
18.【解答】解:(1)原式=263
;
(2)原式=(2)2
=2﹣22
=2.
19.【解答】(1)证明:∵Δ=[﹣(m+5)]2﹣4×1×3m
=m2+10m+25﹣12m
=m2﹣2m+25
=(m﹣1)2+24,
∵(m﹣1)2≥0,
∴Δ>0,
∴无论m取何值,此方程一定有实数根;
(2)解:∵方程一个根为5,
∴25﹣5(m+5)+3m=0,
∴m=0,
∴方程为x2﹣5x=0,
∴x1=0,x2=5,
∴另一个根为0.
20.【解答】(1)证明:∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:设∠BAP=α,
∵△ABE≌△CBE,
∴∠BAP=∠BCE=α,
∵AE=PC,AE=CE,
∴PC=CE,
∴∠CPE=∠CEP(180°﹣∠BCE)=90°α,
∵∠CPE是△ABP的一个外角,∠ABC=45°,
∴∠CPE=∠ABC+∠BAP,
∴90°α=45°+α,
∴α=30°,
∴∠BAP=α=30°.
21.【解答】解:(1)m=10﹣2﹣4﹣1=3,
在75,83,79,89,79,83,95,70,64,83中,出现次数最多的是83,
∴众数a=83;
m=10﹣2﹣4﹣1=3,
八年级成绩中处于中间的两个数据为84和85,
∴中位数b84.5;
故答案为:3,83;84.5;
(2)320192(人),
∴估计该校参加竞赛的八年级320名学生中,竞赛成绩为“优秀”的人数192人;
(3)我认为八年级成绩更好,理由如下:
因为两个年级的平均数相同,而八年级的成绩的中位数和众数均都大于七年级.
22.【解答】解:(1)根据题意得:(360﹣280)×60
=80×60
=4800(元).
答:降价前商场每月销售该商品的利润是4800元;
(2)设每件商品降价m元,则每件的销售利润为(360﹣m﹣280)元,每月可售出(60+5m)件,
根据题意得:(360﹣m﹣280)(60+5m)=7200,
整理得:m2﹣68m+480=0,
解得:m1=8,m2=60,
又∵要有利于减少库存,
∴m=60.
答:每件商品应降价60元;
(3)根据题意得:60+60(1+x)+60(1+x)2=285,
整理得:4x2+12x﹣7=0,
解得:x1=0.5=50%,x2=﹣3.5(不符合题意,舍去),
∴60(1+x)=60×(1+50%)=90(件),60(1+x)2=60×(1+50%)2=135(件),
∴2月份这种商品的售价为360354(元),3月份这种商品的售价为360345(元),
∴该季度的总利润为(360﹣280)×60+(354﹣280)×90+(345﹣280)×135=20235(元).
答:该季度的总利润为20235元.
23.【解答】(1)证明:∵四边形ABCD和四边形AEFG都是正方形,
∴AB=AD,AE=AG,∠EAG=∠BAD=90°,
∴∠EAG﹣∠BAG=∠BAD﹣∠BAG,
即∠EAB=∠GAD,
∴△AEB≌△AGD(SAS);
(2)①证明:由(1)可知△AEB≌△AGD,
∴DG=BE,∠AGD=∠AEB=90°
∴点F,G,D共线.
如图,过点D作DK⊥DG交EG延长线于点K,
∵∠DGK=∠FGE=45°,
∴△DGK是等腰直角三角形,
∴∠K=∠BEO=45°,DK=DG=BE,
又∵∠BOE=∠DOK,
∴△OBE≌△ODK(AAS),
∴BO=DO;
②解:∵AE=3,△AEG为等腰直角三角形,
∵EG=3,,
在Rt△AEB中由勾股定理可得BE1,
∴DK=BE=1,
∴GK,
∴EK=EG+GK=4,
由①知△OBE≌△ODK,
∴OE=OKEK=2,
如图,设EK交CD于点P,作PQ⊥DG于点Q,
设PQ=m,
则GQ=PQ=m,
∵∠EAB+∠BAG=90°=∠BAG+∠GAD=∠GAD+∠ADG=∠ADG+∠PDQ,
∴∠EAB=∠QDP,
∴△ABE∽△DPQ,
∴,
∴DQ=3PQ=3m,
∴DG=4m=1,
∴mPQ,
∴PG,
∵OE=2,
∴OG,
∴OH=OP,
∴OE=2,OH.
24.【解答】(1)证明:∵DE=BF,AQ=BF,
∴AQ=DE,
∵在平行四边形ABCD中,DC∥AB,
∴四边形AQED为平行四边形;
(2)解:过点A作CD的垂线,交CD延长线于点H,连结AC,交EF于点O,如图,
由轴对称性可知:EF垂直平分AC,
∴AE=EC,
在Rt△AHD中,
∵∠HAD=90°﹣∠DAB=30°,
∴DHAD=2,
∴AH=AD cos30°=2,CH=CD+DH=8.
由勾股定理得:AC2,
∴OA=OCAC.
在Rt△AHE中,
由勾股定理得:AH2+HE2=AE2,
设AE=x,则EC=x,HE=8﹣x,
∴(8﹣x)2=x2,
解得:x,
∴AE=EC,
∴OE,
由平行四边形的中心对称性,得EF=2OE.
∴折痕EF的长为.
(3)解:①当点G落在AB边上时,如图,
由折叠性质可知:FG=FB,HE=CE,∠EFG=90°,
∵DE=BF,
∴FG=DE,
在平行四边形ABCD中,
∵AB//CD,
∴四边形DEFG是平行四边形,
∴∠DGA=∠EFG=90°,
在Rt△ADG中,
∵∠ADG=30°,
∴AGAD=2,
∴BG=AB﹣AG=6﹣2=4.
②当点G落在AD边上时,连结BD交EF于点O,连接OG,如图,
由平行四边形的中心对称性,得DO=BO,
由翻折的性质得:GO=BO
∴OG=DO=OBBD,
∴△BGD为直角三角形,∠DGB=90°,
∴BG=AB sin60°=63;
③当点G落在DC边上时,连结BG交EF于点O,如图,
由折叠可知:FG=FB,
∵FB=DE,
∴FG=DE.
则BG垂直平分EF,
由轴对称性可知EF垂直平分BG,
∴点G与点D重合.
过点D作AB的垂线交于点M,
在Rt△BGM中,
∵AMAD=2,GM=DM=2,
∴BM=AB﹣AM=4,
∴由勾股定理,得BG2.
综上所述,点B,G之间的距离为4或3或2.
25.【解答】(1)解:由题意,将m=1代入x2+mx﹣1=0,得x2+x﹣1=0,
∴.
∵黄金分割数大于0,
∴黄金分割数为;
(2)证明:∵b2﹣2mb=4,
∴b2﹣2mb﹣4=0.
∴.
又b≠﹣2a,a2+ma﹣1=0,
∴是一元二次方程x2+mx﹣1=0的两个根;
(3)解:由题意,令p2+np﹣1=q①,q2+nq﹣1=p②,
∴①+②得(p2+q2)+n(p+q)﹣2=p+q,
(p+q)2﹣2pq+n(p+q)﹣2=p+q.
①﹣②得(p2﹣q2)+n(p﹣q)=﹣(p﹣q).
由条件可知p﹣q≠0.
∴(p+q)+n=﹣1,
∴p+q=﹣n﹣1,
又(p+q)2﹣2pq+n(p+q)﹣2=p+q,
∴n2+2n+1﹣2pq﹣n2﹣n﹣2=﹣n﹣1,
∴pq=n,
∴pq﹣n=0.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年八年级下学期数学第三次月考模拟试卷
满分:120分 时间:120分钟 范围:第一章二次根式到第五章特殊平行四边形
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.二次根式中x的取值范围是( )
A.x=2 B.x≥2 C.x>2 D.x<2
2.用反证法证明命题“一个多边形最多有四个内角是直角”时,我们可以先假设( )
A.有三个直角
B.有四个直角
C.至少有四个内角是直角
D.至少有五个内角是直角
3.已知实数a,b在数轴上的位置如图所示,化简的正确结果是( )
A.a+b﹣1 B.1﹣a﹣b C.a﹣b+3 D.b﹣a﹣3
4.下列图标中,是中心对称图形的是( )
A. B. C. D.
5.以下说法正确的是( )
A.菱形的对角线互相垂直且相等
B.矩形的对角线互相平分且互相垂直
C.正方形的对角线互相垂直且平分
D.平行四边形的对角线互相平分且相等
6.如图,在直角坐标系中,菱形OABC的顶点C(3,4),反比例函数图象交线段AB,射线BC于点E,F,连接EF,则S△BEF的值是( )
A.6 B.7 C.8 D.9
7.已知正比例函数y1=﹣2x与反比例函数.对于实数m,当x=m时,y1>y2;当x=m+1时,y1<y2,则m的取值范围为( )
A.m<﹣2或0<m<2 B.﹣2<m<2
C.﹣3<m<﹣2或1<m<2 D.﹣2<m<0或m>2
8.如图,在矩形ABCD中,M是矩形内一点,设△ABM,△ADM,△CDM,△BCM的面积分别表示S1,S2,S3,S4,要求出S3﹣S4的值,只需知道( )
A.S4﹣S1 B.S2﹣S1 C.S3+S2 D.S3﹣S2
9.若一元二次方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围是( )
A.k>1 B.k<1 C.k<1且k≠0 D.k≥1
10.如图,矩形ABCD中,AB=3,AD=5,E,F分别是边AD,BC的中点,CP⊥BE于P,DP的延长线交AB于G.下列结论:①PF=2.5;②PF⊥DG;③.其中结论正确的有( )
A.①② B.②③ C.①③ D.①②③
二、填空题(每小题3分,满分18分)
11.甲、乙两人进行射击测试,每人10次射击平均成绩均为9环,方差分别为:S甲2=2平方环,S乙2=1.5平方环,则射击成绩较稳定的是 (填“甲”或“乙”)
12.若关于x的一元二次方程x2+kx﹣k﹣1=0有两个相等的实数根,则k的值为 .
13.计算一组数据的方差,列式为,则该组数据的方差是 .
14.二次根式在实数范围内有意义,则x的取值范围为 .
15.已知方程3x2+kx﹣2=0的一个根为2,则另一个根为 .
16.如图,已知菱形ABCD的面积为,,点P,Q分别是在边BC,CD上(不与C点重合),且CP=CQ,连结DP,AQ,则DP+AQ的最小值为 .
浙教版2024—2025学年八年级下学期数学第三次月考模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______ ______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.(1)解方程:x(x﹣2)=x﹣2;(2)解方程:(3x﹣4)2=(4x﹣3)2.
18.(1)计算:;(2)计算:.
19.已知关于x的方程x2﹣(m+5)x+3m=0.
(1)求证:无论m取何值,此方程一定有实数根;
(2)若方程有一个实数根是5,求方程的另一个根.
20.如图,在菱形ABCD中,点P是BC边上的点,连结AP交对角线BD于点E,连结EC.
(1)求证:AE=CE.
(2)若∠ABC=45°,AE=PC,求∠BAP的度数.
21.为了进一步加强中小学生对于民族文化的认同感,某中学开展了形式多样的传统文化教育培训活动.为了解培训效果,该校组织全校学生参加了传统文化主题知识竞赛,为了解竞赛成绩,随机抽样调查了七、八年级各10名学生的成绩x(单位:分),分数如下:
七年级10名学生竞赛成绩:75,83,79,89,79,83,95,70,64,83;
八年级10名学生竞赛成绩中分布血80<x≤90的成绩如下:84,85,85,85,86.
【整理数据】:
年级 0<x≤70 70<x≤80 80<x≤90 90<x≤100
七年级 2 m 4 1
八年级 1 3 5 1
【分析数据】:
年级 平均数 众数 中位数 方差
七年级 80 a 81 71.6
八年级 80 85 b 59.8
根据以上提供的信息,回答下列问题:
(1)填空:m= ,a= ,b= ;
(2)若学生的竞赛成绩超过80分为“优秀”,请估计该校参加竞赛的八年级320名学生中,竞赛成绩为“优秀”的人数;
(3)根据以上统计结果,从不同角度说明七年级与八年级哪个年级成绩更优秀.
22.某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件.为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.
(1)降价前商场每月销售该商品的利润是多少元?
(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?
(3)该商场1月份销售量为60件,2月和3月的月平均增长率为x,若前三个月的总销量为285件,求该季度的总利润.
23.含有公共顶点A的正方形ABCD和正方形AEFG按图1所示放置,连结BE,DG.
(1)求证:△AEB≌△AGD.
(2)如图2,把图1中的正方形AEFG绕点A旋转,边EF刚好经过点B,此时对角线EG与正方形ABCD的对角线BD交于点O,与边AB交于点H.
①求证:BO=DO.
②若AE=3,,请直接写出OE和OH的长.
24.在 ABCD中,AB=6,AD=4,∠A=60°,点E,F分别为边CD,AB上异于端点的动点,且DE=BF,连结EF,将四边形CEFB沿着EF折叠得到四边形HEFG.
(1)如图1,边HE,AB交于点Q,若AQ=BF,求证:四边形AQED为平行四边形;
(2)如图2,当点C落在点A处时,求折痕EF的长;
(3)当点G落在 ABCD的边上时,求点B,G之间的距离.
25.关于x的一元二次方程x2+mx﹣1=0,当m=1时,该方程的正根称为黄金分割数.宽与长的比是黄金分割数的矩形叫做黄金矩形,希腊的巴特农神庙采用的就是黄金矩形的设计;我国著名数学家华罗庚的优选法中也应用到了黄金分割数.
(1)求黄金分割数;
(2)已知实数a,b满足a2+ma=1,b2﹣2mb=4,且b≠﹣2a,请证明:a,是一元二次方程x2+mx﹣1=0的两个根;
(3)已知两个不相等的实数p,q满足p2+np﹣1=q,q2+nq﹣1=p,求pq﹣n的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C B C C C B B D
1.【解答】解:由题意可得:x﹣2≥0,
解得:x≥2,
故选:B.
2.【解答】解:用反证法证明命题“一个多边形最多有四个内角是直角”时,首先应该假设至少有五个内角是直角,
故选:D.
3.【解答】解:由实数a,b在数轴上的位置可知,﹣1<a<0<1<b<2,
∴a+1>0,b﹣2<0,
∴原式=|a+1|+|b﹣2|
=a+1﹣b+2
=a﹣b+3.
故选:C.
4.【解答】解:选项A、C、D的图形都不能找到某一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形;
选项B的图形能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形;
故选:B.
5.【解答】解:A、菱形的对角线互相垂直且互相平分,故原选项错误,不符合题意;
B、矩形的对角线互相平分且相等,故原选项错误,不符合题意;
C、正方形的对角线互相垂直且平分,故原选项正确,符合题意;
D、平行四边形的对角线互相平分,故原选项错误,不符合题意.
故选:C.
6.【解答】解:∵C(3,4),
∴OC=BC5,
∴B(8,4),
在反比例函数y中,当y=4时,x=2,
F(2,4),
BF=8﹣2=6.
设直线AB的解析式为y=kx+b,A(5,0)、B(8,4)在直线上,
,解得,
∴直线AB的解析式为yx,
联立方程组,解得,,
∴E(6,),
∴S△BEF8.
故选:C.
7.【解答】解:联立方程组,解得或,
列函数的交点坐标为(2,﹣4),(﹣2,4),
∵当x=m时,y1>y2;
∴m<﹣2,或0<m<2,
∵当x=m+1时,y1<y2,
∴﹣2<m+1<0或m+1>2,
解得:﹣3<m<﹣1,或m>1.
∴﹣3<m<﹣2或1<m<2.
故选:C.
8.【解答】解:如图所示:连接MC,分别过点M作ME⊥AB交AB于点E,MF⊥AD交AD于点F,延长EM交CD于点G,延长FM交BC于点H,
∴∠AEM=∠MGD=90°,∠AFM=∠BHM=90°,
∵四边形ABCD是矩形,
∴∠BAD=∠ADC=∠ABC=∠BCD=90°,
∴四边形AEFM、BHME、MHCG和FMGD都是矩形,
∴AE=MF,BE=MH,EM=AF,MG=DF,
∴MF+MH=AE+BE=AB,EM+MG=AF+DF=AD,
∵△ABM的面积S1,△ADM的面积,△CDM的面积,△BCM的面积,
∴
,
S2+S4
,
∴S1+S3=S2+S4,
∴S3﹣S4=S2﹣S1,
∴要求出S3﹣S4的值,只需知道S2﹣S1,
故选:B.
9【解答】解:由题意知,Δ=4﹣4k>0,
解得:k<1.
故选:B.
10.【解答】解:连接GF,由矩形ABCD中,AB=3,AD=5,E,F分别是边AD,BC的中点,CP⊥BE于P,
得PF=BF=CF=2.5,故①对;
由DEADBC=BF,DE∥BF,
得四边形BEDF是平行四边形,
得BE∥DF,
得CP⊥DF,
由PF=CF,
得CP垂直平分DF,
得PD=CD=3,
得△DPF≌△DCF(SSS),
得∠DPF=∠DCF=90°,即PF⊥DG,故②对;
由∠GPF=∠GBF=90°,PF=BF,GF=GF,
得△GPF≌△GBF(HL),
得BG=PG=x,
由AG2+AD2=GD2,
得(3﹣x)2+52=(3+x)2,
得PG=x,故③对.
故选:D.
二、填空题
11.【解答】解:∵S甲2=2>S乙2=1.5,方差小的为乙,
∴本题中成绩比较稳定的是乙.
故答案为:乙.
12.【解答】解:∵方程x2+kx﹣k﹣1=0有两个相等的实数根,
∴Δ=k2﹣4(﹣k﹣1)=k2+4k+4=(k+2)2=0,
解得:k=﹣2.
故答案为:﹣2.
13.【解答】解:由方差计算公式得这组数据为:2,4,7,5,7,
∴,
∴
=3.6;
故答案为:3.6.
14.【解答】解:∵二次根式在实数范围内有意义,
∴x+2≥0,解得x≥﹣2.
故答案为:x≥﹣2.
15.【解答】解:令方程的另一个根为m,
则2m,
所以m,
即方程的另一个根为.
故答案为:.
16.【解答】解:如图,过点A作AM⊥BC于点M,延长AM到点A′,使A′M=AM,
∵四边形ABCD是菱形,
∴AB=BC=AD,∠ABC=∠ADC,
∵菱形ABCD的面积为,,
∴AM=2,
在Rt△ABM中,根据勾股定理得:
BM1,
以点B为原点,BC为x轴,垂直于BC方向为y轴,建立平面直角坐标系,
∴B(0,0),A(1,2),C(,0),D(1,2),A′(1,﹣2),
∵PC=CQ,BC=CD,
∴BP=DQ,
在△ABP和△ADQ中,
,
∴△ABP≌△ADQ(SAS),
∴AP=AQ=A′P,
连接A′D,AP,A′P,
∵A′P+PD>A′D,
∴A′,P,D三点共线时,PD+A′P取最小值,
∴PD+AQ的最小值=PD+A′P的最小值=A′D.
故答案为:.
三、解答题
17.【解答】解:(1)x(x﹣2)=x﹣2,
x(x﹣2)﹣(x﹣2)=0,
(x﹣2)(x﹣1)=0,
则x﹣2=0或x﹣1=0,
所以x1=2,x2=1.
(2)(3x﹣4)2=(4x﹣3)2,
(3x﹣4)2﹣(4x﹣3)2=0,
(3x﹣4+4x﹣3)(3x﹣4﹣4x+3)=0,
(7x﹣7)(﹣x﹣1)=0,
则7x﹣7=0或﹣x﹣1=0,
所以x1=1,x2=﹣1.
18.【解答】解:(1)原式=263
;
(2)原式=(2)2
=2﹣22
=2.
19.【解答】(1)证明:∵Δ=[﹣(m+5)]2﹣4×1×3m
=m2+10m+25﹣12m
=m2﹣2m+25
=(m﹣1)2+24,
∵(m﹣1)2≥0,
∴Δ>0,
∴无论m取何值,此方程一定有实数根;
(2)解:∵方程一个根为5,
∴25﹣5(m+5)+3m=0,
∴m=0,
∴方程为x2﹣5x=0,
∴x1=0,x2=5,
∴另一个根为0.
20.【解答】(1)证明:∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:设∠BAP=α,
∵△ABE≌△CBE,
∴∠BAP=∠BCE=α,
∵AE=PC,AE=CE,
∴PC=CE,
∴∠CPE=∠CEP(180°﹣∠BCE)=90°α,
∵∠CPE是△ABP的一个外角,∠ABC=45°,
∴∠CPE=∠ABC+∠BAP,
∴90°α=45°+α,
∴α=30°,
∴∠BAP=α=30°.
21.【解答】解:(1)m=10﹣2﹣4﹣1=3,
在75,83,79,89,79,83,95,70,64,83中,出现次数最多的是83,
∴众数a=83;
m=10﹣2﹣4﹣1=3,
八年级成绩中处于中间的两个数据为84和85,
∴中位数b84.5;
故答案为:3,83;84.5;
(2)320192(人),
∴估计该校参加竞赛的八年级320名学生中,竞赛成绩为“优秀”的人数192人;
(3)我认为八年级成绩更好,理由如下:
因为两个年级的平均数相同,而八年级的成绩的中位数和众数均都大于七年级.
22.【解答】解:(1)根据题意得:(360﹣280)×60
=80×60
=4800(元).
答:降价前商场每月销售该商品的利润是4800元;
(2)设每件商品降价m元,则每件的销售利润为(360﹣m﹣280)元,每月可售出(60+5m)件,
根据题意得:(360﹣m﹣280)(60+5m)=7200,
整理得:m2﹣68m+480=0,
解得:m1=8,m2=60,
又∵要有利于减少库存,
∴m=60.
答:每件商品应降价60元;
(3)根据题意得:60+60(1+x)+60(1+x)2=285,
整理得:4x2+12x﹣7=0,
解得:x1=0.5=50%,x2=﹣3.5(不符合题意,舍去),
∴60(1+x)=60×(1+50%)=90(件),60(1+x)2=60×(1+50%)2=135(件),
∴2月份这种商品的售价为360354(元),3月份这种商品的售价为360345(元),
∴该季度的总利润为(360﹣280)×60+(354﹣280)×90+(345﹣280)×135=20235(元).
答:该季度的总利润为20235元.
23.【解答】(1)证明:∵四边形ABCD和四边形AEFG都是正方形,
∴AB=AD,AE=AG,∠EAG=∠BAD=90°,
∴∠EAG﹣∠BAG=∠BAD﹣∠BAG,
即∠EAB=∠GAD,
∴△AEB≌△AGD(SAS);
(2)①证明:由(1)可知△AEB≌△AGD,
∴DG=BE,∠AGD=∠AEB=90°
∴点F,G,D共线.
如图,过点D作DK⊥DG交EG延长线于点K,
∵∠DGK=∠FGE=45°,
∴△DGK是等腰直角三角形,
∴∠K=∠BEO=45°,DK=DG=BE,
又∵∠BOE=∠DOK,
∴△OBE≌△ODK(AAS),
∴BO=DO;
②解:∵AE=3,△AEG为等腰直角三角形,
∵EG=3,,
在Rt△AEB中由勾股定理可得BE1,
∴DK=BE=1,
∴GK,
∴EK=EG+GK=4,
由①知△OBE≌△ODK,
∴OE=OKEK=2,
如图,设EK交CD于点P,作PQ⊥DG于点Q,
设PQ=m,
则GQ=PQ=m,
∵∠EAB+∠BAG=90°=∠BAG+∠GAD=∠GAD+∠ADG=∠ADG+∠PDQ,
∴∠EAB=∠QDP,
∴△ABE∽△DPQ,
∴,
∴DQ=3PQ=3m,
∴DG=4m=1,
∴mPQ,
∴PG,
∵OE=2,
∴OG,
∴OH=OP,
∴OE=2,OH.
24.【解答】(1)证明:∵DE=BF,AQ=BF,
∴AQ=DE,
∵在平行四边形ABCD中,DC∥AB,
∴四边形AQED为平行四边形;
(2)解:过点A作CD的垂线,交CD延长线于点H,连结AC,交EF于点O,如图,
由轴对称性可知:EF垂直平分AC,
∴AE=EC,
在Rt△AHD中,
∵∠HAD=90°﹣∠DAB=30°,
∴DHAD=2,
∴AH=AD cos30°=2,CH=CD+DH=8.
由勾股定理得:AC2,
∴OA=OCAC.
在Rt△AHE中,
由勾股定理得:AH2+HE2=AE2,
设AE=x,则EC=x,HE=8﹣x,
∴(8﹣x)2=x2,
解得:x,
∴AE=EC,
∴OE,
由平行四边形的中心对称性,得EF=2OE.
∴折痕EF的长为.
(3)解:①当点G落在AB边上时,如图,
由折叠性质可知:FG=FB,HE=CE,∠EFG=90°,
∵DE=BF,
∴FG=DE,
在平行四边形ABCD中,
∵AB//CD,
∴四边形DEFG是平行四边形,
∴∠DGA=∠EFG=90°,
在Rt△ADG中,
∵∠ADG=30°,
∴AGAD=2,
∴BG=AB﹣AG=6﹣2=4.
②当点G落在AD边上时,连结BD交EF于点O,连接OG,如图,
由平行四边形的中心对称性,得DO=BO,
由翻折的性质得:GO=BO
∴OG=DO=OBBD,
∴△BGD为直角三角形,∠DGB=90°,
∴BG=AB sin60°=63;
③当点G落在DC边上时,连结BG交EF于点O,如图,
由折叠可知:FG=FB,
∵FB=DE,
∴FG=DE.
则BG垂直平分EF,
由轴对称性可知EF垂直平分BG,
∴点G与点D重合.
过点D作AB的垂线交于点M,
在Rt△BGM中,
∵AMAD=2,GM=DM=2,
∴BM=AB﹣AM=4,
∴由勾股定理,得BG2.
综上所述,点B,G之间的距离为4或3或2.
25.【解答】(1)解:由题意,将m=1代入x2+mx﹣1=0,得x2+x﹣1=0,
∴.
∵黄金分割数大于0,
∴黄金分割数为;
(2)证明:∵b2﹣2mb=4,
∴b2﹣2mb﹣4=0.
∴.
又b≠﹣2a,a2+ma﹣1=0,
∴是一元二次方程x2+mx﹣1=0的两个根;
(3)解:由题意,令p2+np﹣1=q①,q2+nq﹣1=p②,
∴①+②得(p2+q2)+n(p+q)﹣2=p+q,
(p+q)2﹣2pq+n(p+q)﹣2=p+q.
①﹣②得(p2﹣q2)+n(p﹣q)=﹣(p﹣q).
由条件可知p﹣q≠0.
∴(p+q)+n=﹣1,
∴p+q=﹣n﹣1,
又(p+q)2﹣2pq+n(p+q)﹣2=p+q,
∴n2+2n+1﹣2pq﹣n2﹣n﹣2=﹣n﹣1,
∴pq=n,
∴pq﹣n=0.
21世纪教育网(www.21cnjy.com)
同课章节目录
