3.2 代数式 第3课时 课件(共16张PPT) 苏科版(2024)数学七年级上册
文档属性
| 名称 | 3.2 代数式 第3课时 课件(共16张PPT) 苏科版(2024)数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-17 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
3.2 代数式(3)
情境引入
据报纸记载,一位医生研究得出由父母身高预测子女成年后身高的公式:儿子身高是由父母身高的和的一半,再乘以1.08;女儿的身高是父亲身高的0.923倍加上母亲身高的和再除以2.
导入新课
(1)已知父亲身高是a米,母亲身高是b米,试用代数式表示儿子和女儿的身高;
(2)五年级女生小红的父亲身高是1.75米,母亲的身高是1.62米;六年级男生小明的父亲的身高是1.70,母亲的身高是1.62,试预测成年以后小明与小红谁个子高?
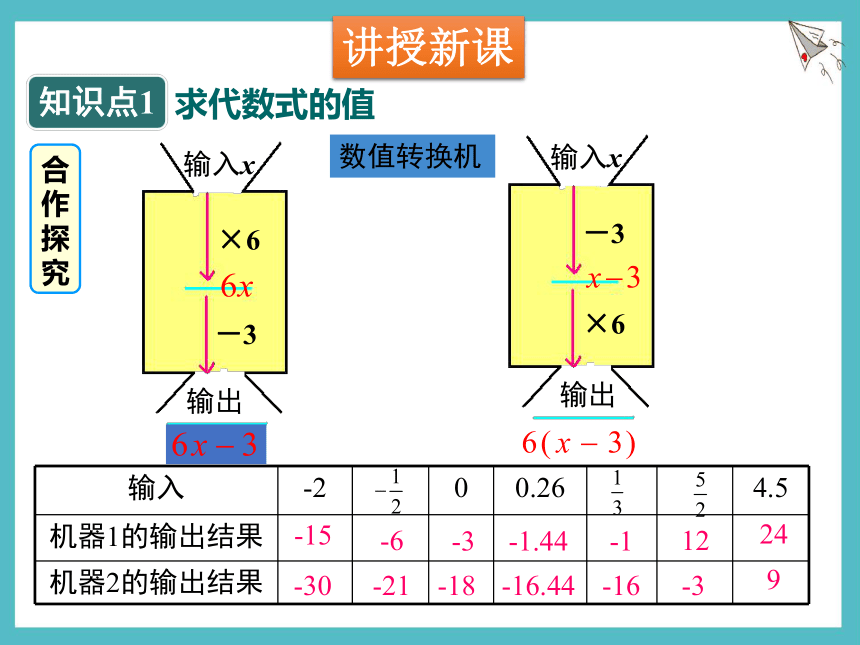
合作探究
数值转换机
输入 -2 0 0.26 4.5
机器1的输出结果
机器2的输出结果
输入x
输入x
输出
输出
×6
-3
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
×6
-3
讲授新课
求代数式的值
知识点1
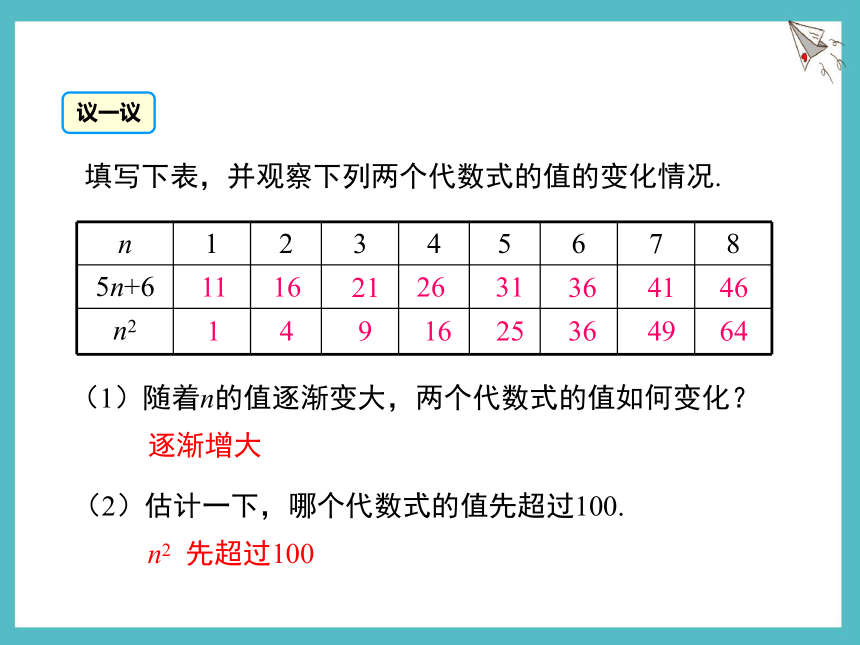
议一议
n 1 2 3 4 5 6 7 8
5n+6
n2
11
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
16
21
26
31
36
41
46
1
4
9
16
25
36
49
64
逐渐增大
n2 先超过100
填写下表,并观察下列两个代数式的值的变化情况.
典例精析
【总结】 代数式的值是由其所含的字母的取值所确定的,并随字母取值的变化而变化,字母取不同的值时,代数式的值可能不同,也可能相同.
整体代入求值
知识点2
练一练
1.已知 则 的值是多少?
解:
由
可得
将
代入上式:
2.当x=1时,代数式 ,当x=-1时,该代数式的值是多少?
解:将x=1代入代数式,得a+b=2017,当x=-1时,
1.当a=2,b=1,c=3时代数式c-(c-a)(c-b)的值是( )
A. 1 B. 2 C.3 D.4
A
2.如果2a+3b=5,那么4a+6b-7=__.
3
3.已知a+b=5,ab=6 ,则ab-(a+b)=___.
1
4.如图所示是一数值转换机,若输入的x为-5,则输出的结果为_______.
49
随堂练习
5.当x=-3,y=2时,求下列代数式的值:
解:
当x=-3,y=2时
6.已知 b=2,求代数式 的值.
解:当 b=2时,
7.某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 优惠办法
少于200元 不予优惠
低于500元但 不低于200元 九折优惠
500元或超过500元 其中500元部分给予九折优惠,
超过500元部分给予八折优惠
(1)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他应付款________元,当x大于或等于500元时,他应付款____________元(用含x的代数式表示);
0.9x
(0.8x+50)
(2)王老师一次性购物600元,他实际付款________元;
(3)王老师第一次购物用了170元,第二次购物用了387元,如果王老师将这两次的购物换作一次购买可以节省________元.
(3)解析:200×0.9=180,500×0.9=450,所以设第二次购物原价为x,则0.9x=387,x=430,两次购物的原价是170+430=600(元),所以如果一次购买只需530元,节省27元.
530
27
代数式的求值
直接代入求值
数值转换机
整体代入求值
课堂小结
3.2 代数式(3)
情境引入
据报纸记载,一位医生研究得出由父母身高预测子女成年后身高的公式:儿子身高是由父母身高的和的一半,再乘以1.08;女儿的身高是父亲身高的0.923倍加上母亲身高的和再除以2.
导入新课
(1)已知父亲身高是a米,母亲身高是b米,试用代数式表示儿子和女儿的身高;
(2)五年级女生小红的父亲身高是1.75米,母亲的身高是1.62米;六年级男生小明的父亲的身高是1.70,母亲的身高是1.62,试预测成年以后小明与小红谁个子高?
合作探究
数值转换机
输入 -2 0 0.26 4.5
机器1的输出结果
机器2的输出结果
输入x
输入x
输出
输出
×6
-3
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
×6
-3
讲授新课
求代数式的值
知识点1
议一议
n 1 2 3 4 5 6 7 8
5n+6
n2
11
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
16
21
26
31
36
41
46
1
4
9
16
25
36
49
64
逐渐增大
n2 先超过100
填写下表,并观察下列两个代数式的值的变化情况.
典例精析
【总结】 代数式的值是由其所含的字母的取值所确定的,并随字母取值的变化而变化,字母取不同的值时,代数式的值可能不同,也可能相同.
整体代入求值
知识点2
练一练
1.已知 则 的值是多少?
解:
由
可得
将
代入上式:
2.当x=1时,代数式 ,当x=-1时,该代数式的值是多少?
解:将x=1代入代数式,得a+b=2017,当x=-1时,
1.当a=2,b=1,c=3时代数式c-(c-a)(c-b)的值是( )
A. 1 B. 2 C.3 D.4
A
2.如果2a+3b=5,那么4a+6b-7=__.
3
3.已知a+b=5,ab=6 ,则ab-(a+b)=___.
1
4.如图所示是一数值转换机,若输入的x为-5,则输出的结果为_______.
49
随堂练习
5.当x=-3,y=2时,求下列代数式的值:
解:
当x=-3,y=2时
6.已知 b=2,求代数式 的值.
解:当 b=2时,
7.某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 优惠办法
少于200元 不予优惠
低于500元但 不低于200元 九折优惠
500元或超过500元 其中500元部分给予九折优惠,
超过500元部分给予八折优惠
(1)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他应付款________元,当x大于或等于500元时,他应付款____________元(用含x的代数式表示);
0.9x
(0.8x+50)
(2)王老师一次性购物600元,他实际付款________元;
(3)王老师第一次购物用了170元,第二次购物用了387元,如果王老师将这两次的购物换作一次购买可以节省________元.
(3)解析:200×0.9=180,500×0.9=450,所以设第二次购物原价为x,则0.9x=387,x=430,两次购物的原价是170+430=600(元),所以如果一次购买只需530元,节省27元.
530
27
代数式的求值
直接代入求值
数值转换机
整体代入求值
课堂小结
同课章节目录
