冀教版六年级上册数学第4课时 比例的基本性质(课件)(共17张PPT)
文档属性
| 名称 | 冀教版六年级上册数学第4课时 比例的基本性质(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-18 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
比和比例
第4课时 比例的基本性质
冀教版 数学 六年级 上册
1.经历自主探索比例基本性质以及应用性质解比例的过程。
2.理解比例的基本性质,会运用比例的基本性质解比例。
3.在探索比例的基本性质和解比例的过程中,获得成功的体验,树立学好数学的信心。
试着写出2个比值是1.5的比。
240∶160=1.5
144∶96=1.5
你能把它们组成比例吗?
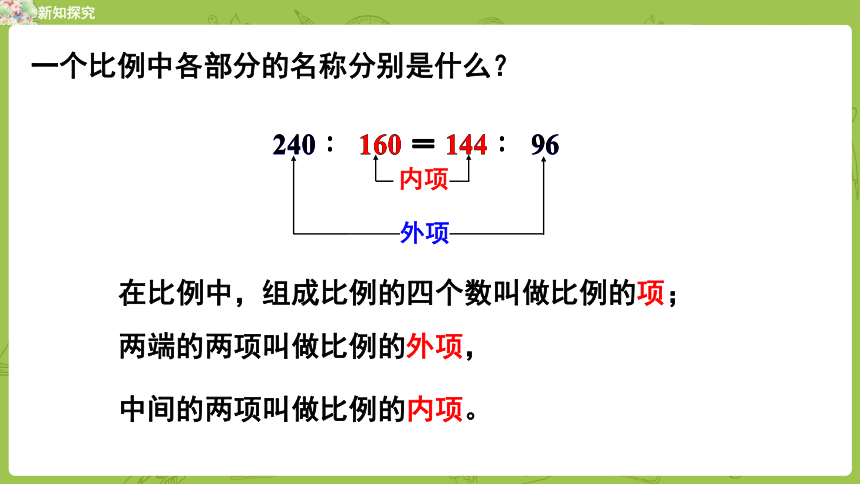
在比例中,组成比例的四个数叫做比例的项;
内项
外项
两端的两项叫做比例的外项,
中间的两项叫做比例的内项。
240 ∶ 160 = 144 ∶ 96
一个比例中各部分的名称分别是什么?
240 ∶ 160 = 144 ∶ 96
240 ∶ 160 = 144 ∶ 96
把240 ∶ 160 = 144 ∶ 96中的两个外项、两个内项分别相乘,你发现了什么?
两个外项的积等于两个内项的积。
自己写出一组比例,也按照上面的方法乘一下,看是否也得到同样的规律。
正确
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
你能用字母表示这个性质吗?
ad=bc。
如果用字母表示比例的四个项,即 a∶b=c∶d
(b、d≠0),
那么比例的基本性质可以表示为
你能把下面的比例改成分数形式吗?
240 ∶ 160 = 144 ∶ 96
内项
外项
240
160
144
96
=
内项
内项
外项
外项
如果把比例写成分数形式,等号两端的分子和分母分别交叉相乘,它们的积相等。
根据比例的基本性质可以判断两个比能不能组成比例。
你知道比和比例的区别和联系吗?
根据比例的基本性质,如果已知比例中的任何三项,都可以求出另外一个未知项。
求比例中的未知项,叫做解比例。
(1)9∶2 = 6∶x
(2)∶x = ∶
解:
9x = 2×6
x =
解比例。
x =
解:
x = ×
x = ×2
x =
将比例转化成一般方程,再通过解方程求出未知项。
解比例。
解:
x=1.2÷0.3
x=4
解:
x=96×36÷24
x=144
1
96∶24=x∶36
0.6∶x=0.3∶2
0.3x=0.6×2
解:
解:
x =91×8÷26
x =28
1
解比例。
x = × ÷13
x =
填空。
(1)将2、5、8再配上一个数组成比例,这个数可以是( )。
(2)先写出比值都是一的两个比( )和( ),再组成比例( )。
(3)在比例里两个外项互为倒数,其中的一个内项是,另一个内项是( )。
(4)如果7a=5b,则a:b=( ):( )。
2
易错举例
判断。
(1)两个比就可以组成一个比例。( )
(2)比例的两个内项的积减去两个外项的积一定是0。( )
(3)如果 9a=6b,那么a:b=3:2。( )
智力乐园
一个比例的两个外项分别是25和10,两个比的比值是一,你能写出这个比例吗
解答:先根据比值和已知的两个外项,分别求出两个内项,再写出比例。此比例不唯一。
25: =4:10
(3)算一算,如果竹竿的高度是3.5米,影子的长是多少米?
解:设影子的长是 x 米。
1∶0.5=3.5∶ x
x =3.5×0.5
x =1.75
答:影子的长是1.75米。
2
这节课你有什么收获?
比例各部分的名称:组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
(判断两个比能否成比例的依据)
解比例:求比例中的未知项,叫做解比例。
(解比例的关键:利用比例的基本性质将比例式转化成一般方程。)
如果 a∶b=c∶d 或
a
b
c
d
=
(b、d≠0),那么ad=bc。
比和比例
第4课时 比例的基本性质
冀教版 数学 六年级 上册
1.经历自主探索比例基本性质以及应用性质解比例的过程。
2.理解比例的基本性质,会运用比例的基本性质解比例。
3.在探索比例的基本性质和解比例的过程中,获得成功的体验,树立学好数学的信心。
试着写出2个比值是1.5的比。
240∶160=1.5
144∶96=1.5
你能把它们组成比例吗?
在比例中,组成比例的四个数叫做比例的项;
内项
外项
两端的两项叫做比例的外项,
中间的两项叫做比例的内项。
240 ∶ 160 = 144 ∶ 96
一个比例中各部分的名称分别是什么?
240 ∶ 160 = 144 ∶ 96
240 ∶ 160 = 144 ∶ 96
把240 ∶ 160 = 144 ∶ 96中的两个外项、两个内项分别相乘,你发现了什么?
两个外项的积等于两个内项的积。
自己写出一组比例,也按照上面的方法乘一下,看是否也得到同样的规律。
正确
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
你能用字母表示这个性质吗?
ad=bc。
如果用字母表示比例的四个项,即 a∶b=c∶d
(b、d≠0),
那么比例的基本性质可以表示为
你能把下面的比例改成分数形式吗?
240 ∶ 160 = 144 ∶ 96
内项
外项
240
160
144
96
=
内项
内项
外项
外项
如果把比例写成分数形式,等号两端的分子和分母分别交叉相乘,它们的积相等。
根据比例的基本性质可以判断两个比能不能组成比例。
你知道比和比例的区别和联系吗?
根据比例的基本性质,如果已知比例中的任何三项,都可以求出另外一个未知项。
求比例中的未知项,叫做解比例。
(1)9∶2 = 6∶x
(2)∶x = ∶
解:
9x = 2×6
x =
解比例。
x =
解:
x = ×
x = ×2
x =
将比例转化成一般方程,再通过解方程求出未知项。
解比例。
解:
x=1.2÷0.3
x=4
解:
x=96×36÷24
x=144
1
96∶24=x∶36
0.6∶x=0.3∶2
0.3x=0.6×2
解:
解:
x =91×8÷26
x =28
1
解比例。
x = × ÷13
x =
填空。
(1)将2、5、8再配上一个数组成比例,这个数可以是( )。
(2)先写出比值都是一的两个比( )和( ),再组成比例( )。
(3)在比例里两个外项互为倒数,其中的一个内项是,另一个内项是( )。
(4)如果7a=5b,则a:b=( ):( )。
2
易错举例
判断。
(1)两个比就可以组成一个比例。( )
(2)比例的两个内项的积减去两个外项的积一定是0。( )
(3)如果 9a=6b,那么a:b=3:2。( )
智力乐园
一个比例的两个外项分别是25和10,两个比的比值是一,你能写出这个比例吗
解答:先根据比值和已知的两个外项,分别求出两个内项,再写出比例。此比例不唯一。
25: =4:10
(3)算一算,如果竹竿的高度是3.5米,影子的长是多少米?
解:设影子的长是 x 米。
1∶0.5=3.5∶ x
x =3.5×0.5
x =1.75
答:影子的长是1.75米。
2
这节课你有什么收获?
比例各部分的名称:组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
(判断两个比能否成比例的依据)
解比例:求比例中的未知项,叫做解比例。
(解比例的关键:利用比例的基本性质将比例式转化成一般方程。)
如果 a∶b=c∶d 或
a
b
c
d
=
(b、d≠0),那么ad=bc。
