苏教版六年级上册数学3.8按比例分配的实际问题课件(共17张PPT)
文档属性
| 名称 | 苏教版六年级上册数学3.8按比例分配的实际问题课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 918.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-18 08:23:17 | ||
图片预览






文档简介
(共17张PPT)
苏教版六年级数学上册
3.8 按比例分配的实际问题
学习目标
1、使学生理解按比例分配实际问题的意义。
2、使学生通过运用比的意义和基本性质解答
有关按比例分配的实际问题。
重点:认识按比例分配实际问题的数量关系和解答方法。
难点:理解按比例分配实际问题的数量关系,
一、复习引入:
1、将7:5的后项增加15,要使比值不变,前项应( )。
A.增加15 B.乘3 C.增加21 D.增加14
2、把20克盐放入200克水中,盐和盐水的比是( )。
A.10:1 B.11:1 C.1:10 D.1:11
把20克盐放入200克水中,
那么配制这样的盐水1320千克,
需盐多少千克?水多少千克?
C
D
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?
先算一算,再涂一涂。
红色方格数是黄色的
黄色方格数是红色的
二、探究新知:
红色、黄色方格数分别占总格数的几分之几?
红色方格数占总格数的
30×
=30×
=18(格)
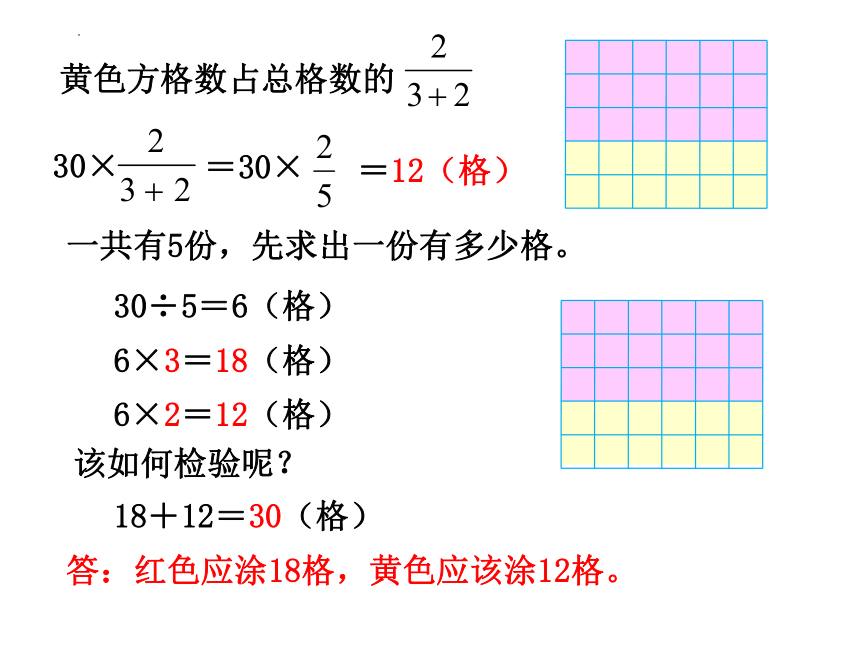
黄色方格数占总格数的
30×
=30×
=12(格)
一共有5份,先求出一份有多少格。
30÷5=6(格)
6×3=18(格)
6×2=12(格)
该如何检验呢?
18+12=30(格)
答:红色应涂18格,黄色应该涂12格。
30个方格按1:2:3涂成红、黄、绿三种颜色,
三种颜色各应涂多少格?
红色方格数占总格数的
黄色方格数占总格数的
绿色方格数占总格数的
5格
10格
15格
各占总格数的多少?
答:红色应涂5格,黄色应该涂10格,绿色应涂15格。
试一试:
三个小组去植树,植树棵数按各小组人数的比分配。每个小组各应植树多少棵?
72棵树;一组8人;二组7人,三组9人
8+7+9=24(人)
72÷24×8=24(棵)
72÷24×7=21(棵)
72÷24×9=27(棵)
答:一组、二组、三组分别应植树24棵、21棵、27棵。
三个小组去植树,植树棵数按各小组人数的比分配。
每个小组各应植树多少棵?
72棵树;一组8人;二组7人,三组9人
72×
=24(棵)
72×
=21(棵)
72×
=27(棵)
答:一组、二组、三组分别应植树24棵、21棵、27棵。
小结:
把一个数量按照一定的比分配,
这种方法通常叫做按比分配。
根据分配总量一共有几份,再看要求的部分有几份,然后用先除后乘的方法解答;
也可以转化成分数乘法应用题解答。
1、按比分配的概念:
3、平均分是按比分配的一个特例。
2、按比分配计算方法。
例题讲解:
例1、学校买回科技书60本,按照六年级三个班人数的比分配到各班,一班有34人,二班有40人,三班有46人,三个班各分到科技书多少本?
34:40:46=17:20:23
60÷(17+20+23)×17=17(本)
60÷(17+20+23)×20=20(本)
60÷(17+20+23)×23=23(本)
答:一班分到17本,二班分到20本,三班分到23本。
例2、春节到了,朵朵家包了白菜猪肉包、韭菜粉丝包和麻婆豆腐包共120个。其中白菜猪肉包和韭菜粉丝包的数量比是2:3,韭菜粉丝包和麻婆豆腐包的数量比是6:5。三种包子各有多少个
三、独立训练
1、牡丹园的粉牡丹和黄牡丹共有45株,粉牡丹
和黄牡丹的株数比可能是( )
A.3:8 B.4:5 C. 5:2 D.6:1
2、一个三角形三个内角的度数比是2:5:3,
这个三角形是 ( ).
A.直角三角形 B.钝角三角形
C.锐角三角形 D.等腰三角形
4、水果店有苹果和梨子共80千克,苹果和梨子总量的比是3∶5,水果店有苹果和梨子各多少千克?
四、拓展提高
用72分米长的铁丝焊一个长方体框架,长、宽、高的比是4:3:2,这个长方体框架的体积是多少立方分米
(不考虑耗损)
五、总结反思
把一个数量按照一定的比分配,
这种方法通常叫做按比分配。
根据分配总量一共有几份,再看要求的部分有几份,然后用先除后乘的方法解答;
也可以转化成分数乘法应用题解答。
1、按比分配的概念:
3、平均分是按比分配的一个特例。
2、按比分配计算方法。
六、随堂检测
1、周日,小明按5:3的比安排一天的活动与睡眠时间。
他周日这天的睡眠时间是( )小时。
2、红领巾的形状是等腰三角形,一个底角与顶角
的度数比是1:4,它的顶角是( ),一个底角是( )。
3、张叔叔、刘叔叔、王叔叔三人合作投资开办
一家网络公司,张叔叔投资40万元,刘叔叔投资50万元,王叔叔投资60万元。公司去年获得利润75万元。
如果按照投资金额的比来分配,那么他们三人
各应分得多少万元的利润
苏教版六年级数学上册
3.8 按比例分配的实际问题
学习目标
1、使学生理解按比例分配实际问题的意义。
2、使学生通过运用比的意义和基本性质解答
有关按比例分配的实际问题。
重点:认识按比例分配实际问题的数量关系和解答方法。
难点:理解按比例分配实际问题的数量关系,
一、复习引入:
1、将7:5的后项增加15,要使比值不变,前项应( )。
A.增加15 B.乘3 C.增加21 D.增加14
2、把20克盐放入200克水中,盐和盐水的比是( )。
A.10:1 B.11:1 C.1:10 D.1:11
把20克盐放入200克水中,
那么配制这样的盐水1320千克,
需盐多少千克?水多少千克?
C
D
把30个方格涂上红色和黄色,使红色与黄色方格数的比是3:2。两种颜色各应涂多少格?
先算一算,再涂一涂。
红色方格数是黄色的
黄色方格数是红色的
二、探究新知:
红色、黄色方格数分别占总格数的几分之几?
红色方格数占总格数的
30×
=30×
=18(格)
黄色方格数占总格数的
30×
=30×
=12(格)
一共有5份,先求出一份有多少格。
30÷5=6(格)
6×3=18(格)
6×2=12(格)
该如何检验呢?
18+12=30(格)
答:红色应涂18格,黄色应该涂12格。
30个方格按1:2:3涂成红、黄、绿三种颜色,
三种颜色各应涂多少格?
红色方格数占总格数的
黄色方格数占总格数的
绿色方格数占总格数的
5格
10格
15格
各占总格数的多少?
答:红色应涂5格,黄色应该涂10格,绿色应涂15格。
试一试:
三个小组去植树,植树棵数按各小组人数的比分配。每个小组各应植树多少棵?
72棵树;一组8人;二组7人,三组9人
8+7+9=24(人)
72÷24×8=24(棵)
72÷24×7=21(棵)
72÷24×9=27(棵)
答:一组、二组、三组分别应植树24棵、21棵、27棵。
三个小组去植树,植树棵数按各小组人数的比分配。
每个小组各应植树多少棵?
72棵树;一组8人;二组7人,三组9人
72×
=24(棵)
72×
=21(棵)
72×
=27(棵)
答:一组、二组、三组分别应植树24棵、21棵、27棵。
小结:
把一个数量按照一定的比分配,
这种方法通常叫做按比分配。
根据分配总量一共有几份,再看要求的部分有几份,然后用先除后乘的方法解答;
也可以转化成分数乘法应用题解答。
1、按比分配的概念:
3、平均分是按比分配的一个特例。
2、按比分配计算方法。
例题讲解:
例1、学校买回科技书60本,按照六年级三个班人数的比分配到各班,一班有34人,二班有40人,三班有46人,三个班各分到科技书多少本?
34:40:46=17:20:23
60÷(17+20+23)×17=17(本)
60÷(17+20+23)×20=20(本)
60÷(17+20+23)×23=23(本)
答:一班分到17本,二班分到20本,三班分到23本。
例2、春节到了,朵朵家包了白菜猪肉包、韭菜粉丝包和麻婆豆腐包共120个。其中白菜猪肉包和韭菜粉丝包的数量比是2:3,韭菜粉丝包和麻婆豆腐包的数量比是6:5。三种包子各有多少个
三、独立训练
1、牡丹园的粉牡丹和黄牡丹共有45株,粉牡丹
和黄牡丹的株数比可能是( )
A.3:8 B.4:5 C. 5:2 D.6:1
2、一个三角形三个内角的度数比是2:5:3,
这个三角形是 ( ).
A.直角三角形 B.钝角三角形
C.锐角三角形 D.等腰三角形
4、水果店有苹果和梨子共80千克,苹果和梨子总量的比是3∶5,水果店有苹果和梨子各多少千克?
四、拓展提高
用72分米长的铁丝焊一个长方体框架,长、宽、高的比是4:3:2,这个长方体框架的体积是多少立方分米
(不考虑耗损)
五、总结反思
把一个数量按照一定的比分配,
这种方法通常叫做按比分配。
根据分配总量一共有几份,再看要求的部分有几份,然后用先除后乘的方法解答;
也可以转化成分数乘法应用题解答。
1、按比分配的概念:
3、平均分是按比分配的一个特例。
2、按比分配计算方法。
六、随堂检测
1、周日,小明按5:3的比安排一天的活动与睡眠时间。
他周日这天的睡眠时间是( )小时。
2、红领巾的形状是等腰三角形,一个底角与顶角
的度数比是1:4,它的顶角是( ),一个底角是( )。
3、张叔叔、刘叔叔、王叔叔三人合作投资开办
一家网络公司,张叔叔投资40万元,刘叔叔投资50万元,王叔叔投资60万元。公司去年获得利润75万元。
如果按照投资金额的比来分配,那么他们三人
各应分得多少万元的利润
