7.4二元一次方程与一次函数第1课时二元一次方程与一次函数(1)课件(共17张PPT)
文档属性
| 名称 | 7.4二元一次方程与一次函数第1课时二元一次方程与一次函数(1)课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 620.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 11:45:24 | ||
图片预览






文档简介
(共17张PPT)
第七章 二元一次方程组
7.4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数(1)
两条直线平行,有 个交点;
两条直线重合,有 个交点;
两条直线相交,有 个交点;
0
无数
一
1、方程组 有 个解;
2、方程组 有 个解;
3、方程组 有 个解;
0
无数
一
7.4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数(1)
1、初步理解二元一次方程与一次函数的关系;
2、能根据一次函数的图象求二元一次方程组的近似解.
一次函数
这是怎么回事?
二元一次方程
x+y=5这是什么?
7.4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数(1)
方程x+y=5可以转化为:
任意一个二元一次方程都可以转化成y=kx+b的形式,所以每个二元一次方程都对应一个一次函数.
归纳:
思考:是不是任意的二元一次方程 都能进行这样的转换呢?
y=﹣x+5
(1)方程x+y=5有解______个,
(2)在直角坐标系中分别描出以这些解为坐标的点,它们都在函数y=﹣x+5上吗
(0,5) ,(5,0) ,(1,4) 都在函数y=﹣x+5的图象上。
(3)在一次函数y=﹣x+5的图象上任取一个点,它的坐标适合方程x+y=5吗
在一次函数y=﹣x+5的图象上任取一个点,它的坐标适合方程x+y=5。
(4)以方程x+y=5的解为坐标的所有的点所组成的图象与一次函数y=﹣x+5的图象相同吗
相同。
无数
如:(0,5) ,(5,0) ,(1,4)
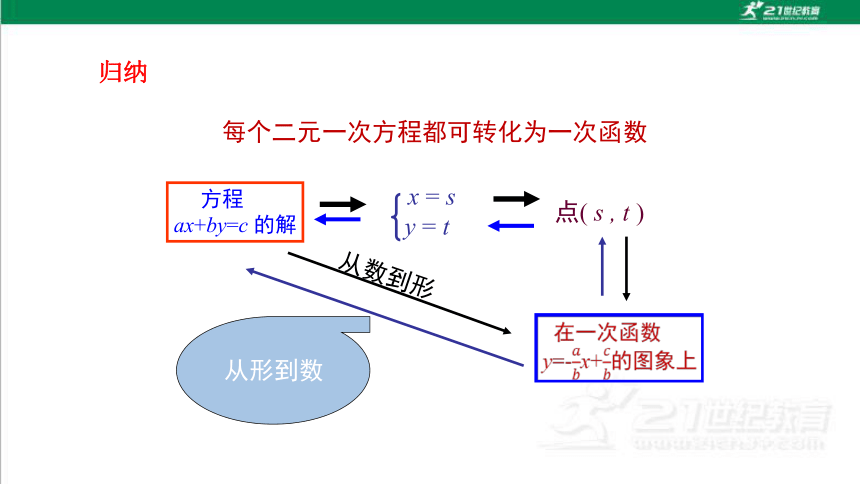
点( s , t )
x = s
y = t
方程
ax+by=c 的解
从形到数
从数到形
每个二元一次方程都可转化为一次函数
归纳
通过以上结论,你能分析研究出二元一次方程与 一次函数图象的关系吗
二元一次方程的解就是相应一次函数图象上的点的坐标;
一次函数图象上的点的坐标就是相应二元一次方程的解.
二元一次方程与一次函数的基本关系
探究
y=5-x
y=2x-1
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=2x-1
y=5-x
P(2,3)
x=2,
y=3。
x+y=5,
2x-y=1
的解是
(1)在同一直角坐标系中分别作一次函数y=5-x和y=2x-1的图象
(0,5)(5,0)
(0,-1)(0.5,0)
(2)函数y=5-x和y=2x-1的图象的交点坐标是:
(2,3)
(3)交点坐标(2,3)与方程组 的解有什么关系?
x+y=5,
2x-y=1
做一做
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
P(2,2)
y=2x-2
x=2,
y=2。
所以方程组的解为
解: 由(1)得
进而作出 的图象。
x-2y=-2 , ①
2x-y=2 。 ②
例:用图象法解二元一次方程组
由(2)得
x=0,
y=-2,
x=1,
y=0。
由此可得
进而作出 的图象。
x=0,
y=1,
x=-2,
y=0。
由此可得
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
练习:
P21
随堂练习2
6
5
y=2-x
y=5-x
没有一组数同时适合方程x+y=2和x+y=5,一次函数y=2-x与y=5-x的图像没有交点。
方程组 解的情况如何?
你能从函数角度解释一下吗?
想一想
1、方程组 有 个解;
2、方程组 有 个解;
3、方程组 有 个解。
0
无数
一
从函数角度解释:
想一想
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组 的解为 .
2、若二元一次方程组 的解为
则函数 与 的图象的交点坐
标为 .
(2,2)
3、根据下列图象,你能说出哪些方程组的解
这些解是什么
-2
1
x
y
O
1
1
x
y
O
求直线 与直线 的交点坐标。
你有哪些方法 与同伴交流,并一起分析各种方法的利弊.
思路2:由解方程组,得到交点坐标.
(把形的问题归结为数的解决,便捷准确)
思路l:画出图象找出交点,确定交点坐标近似值.
(因作图误差可能有较大差别)
探究
(1)二元一次方程与一次函数的区别与联系
(2) 二元一次方程组的解法总共学习了哪几种
加减法;代入法;图象法.
二元一次方程的解就是相应一次函数图象上的点的坐标;
一次函数图象上的点的坐标就是相应二元一次方程的解.
7.4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数(1)
(3)方法归纳
用图象法解二元一次方程组
优点:方法简便,形象直观;体现了数形结合思想.
不足:一般情况下求出的是近似数;要想精确还要
用代数方法,进行细致计算.
第七章 二元一次方程组
7.4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数(1)
两条直线平行,有 个交点;
两条直线重合,有 个交点;
两条直线相交,有 个交点;
0
无数
一
1、方程组 有 个解;
2、方程组 有 个解;
3、方程组 有 个解;
0
无数
一
7.4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数(1)
1、初步理解二元一次方程与一次函数的关系;
2、能根据一次函数的图象求二元一次方程组的近似解.
一次函数
这是怎么回事?
二元一次方程
x+y=5这是什么?
7.4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数(1)
方程x+y=5可以转化为:
任意一个二元一次方程都可以转化成y=kx+b的形式,所以每个二元一次方程都对应一个一次函数.
归纳:
思考:是不是任意的二元一次方程 都能进行这样的转换呢?
y=﹣x+5
(1)方程x+y=5有解______个,
(2)在直角坐标系中分别描出以这些解为坐标的点,它们都在函数y=﹣x+5上吗
(0,5) ,(5,0) ,(1,4) 都在函数y=﹣x+5的图象上。
(3)在一次函数y=﹣x+5的图象上任取一个点,它的坐标适合方程x+y=5吗
在一次函数y=﹣x+5的图象上任取一个点,它的坐标适合方程x+y=5。
(4)以方程x+y=5的解为坐标的所有的点所组成的图象与一次函数y=﹣x+5的图象相同吗
相同。
无数
如:(0,5) ,(5,0) ,(1,4)
点( s , t )
x = s
y = t
方程
ax+by=c 的解
从形到数
从数到形
每个二元一次方程都可转化为一次函数
归纳
通过以上结论,你能分析研究出二元一次方程与 一次函数图象的关系吗
二元一次方程的解就是相应一次函数图象上的点的坐标;
一次函数图象上的点的坐标就是相应二元一次方程的解.
二元一次方程与一次函数的基本关系
探究
y=5-x
y=2x-1
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=2x-1
y=5-x
P(2,3)
x=2,
y=3。
x+y=5,
2x-y=1
的解是
(1)在同一直角坐标系中分别作一次函数y=5-x和y=2x-1的图象
(0,5)(5,0)
(0,-1)(0.5,0)
(2)函数y=5-x和y=2x-1的图象的交点坐标是:
(2,3)
(3)交点坐标(2,3)与方程组 的解有什么关系?
x+y=5,
2x-y=1
做一做
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
P(2,2)
y=2x-2
x=2,
y=2。
所以方程组的解为
解: 由(1)得
进而作出 的图象。
x-2y=-2 , ①
2x-y=2 。 ②
例:用图象法解二元一次方程组
由(2)得
x=0,
y=-2,
x=1,
y=0。
由此可得
进而作出 的图象。
x=0,
y=1,
x=-2,
y=0。
由此可得
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
练习:
P21
随堂练习2
6
5
y=2-x
y=5-x
没有一组数同时适合方程x+y=2和x+y=5,一次函数y=2-x与y=5-x的图像没有交点。
方程组 解的情况如何?
你能从函数角度解释一下吗?
想一想
1、方程组 有 个解;
2、方程组 有 个解;
3、方程组 有 个解。
0
无数
一
从函数角度解释:
想一想
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组 的解为 .
2、若二元一次方程组 的解为
则函数 与 的图象的交点坐
标为 .
(2,2)
3、根据下列图象,你能说出哪些方程组的解
这些解是什么
-2
1
x
y
O
1
1
x
y
O
求直线 与直线 的交点坐标。
你有哪些方法 与同伴交流,并一起分析各种方法的利弊.
思路2:由解方程组,得到交点坐标.
(把形的问题归结为数的解决,便捷准确)
思路l:画出图象找出交点,确定交点坐标近似值.
(因作图误差可能有较大差别)
探究
(1)二元一次方程与一次函数的区别与联系
(2) 二元一次方程组的解法总共学习了哪几种
加减法;代入法;图象法.
二元一次方程的解就是相应一次函数图象上的点的坐标;
一次函数图象上的点的坐标就是相应二元一次方程的解.
7.4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数(1)
(3)方法归纳
用图象法解二元一次方程组
优点:方法简便,形象直观;体现了数形结合思想.
不足:一般情况下求出的是近似数;要想精确还要
用代数方法,进行细致计算.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
