8.1定义与命题第2课时定义与命题(2)课件(共14张PPT)
文档属性
| 名称 | 8.1定义与命题第2课时定义与命题(2)课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 228.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第八章 平行线的有关证明
8.1 定义与命题
第2课时 定义与命题(2)
下列句子是不是命题
(1)如果a=b,那么a+c=b+c;
(2)作线段AB = CD;
(3)三个角对应相等的两个三角形一定全等;
(4)负数都小于零;
(5) ∠A = 90°吗?
是
不是
是
是
不是
8.1 定义与命题
第2课时 定义与命题(2)
合作学习: 观察下列命题,思考:这些命题有什么共同的形式?对于每一个命题,都由几部分组成?分别是哪几部分?
1、如果两个三角形的三条边对应相等,
那么这两个三角形全等;
2、如果a=b,那么a2=b2;
3、如果一个三角形是等腰三角形,
那么这个三角形的两个底角相等;
4、如果两个三角形中有两边和一个角分别相等,
那么这两个三角形全等;
5、如果两个角是内错角,那么它们相等。
8.1 定义与命题
第2课时 定义与命题(2)
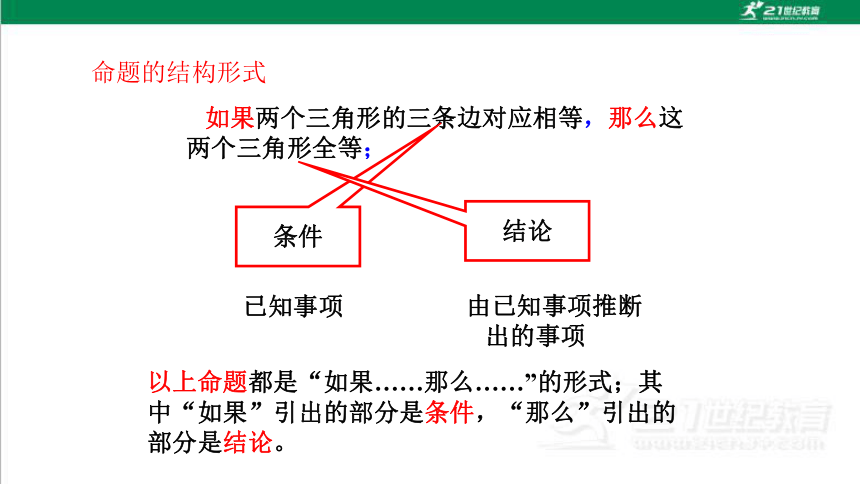
如果两个三角形的三条边对应相等,那么这两个三角形全等;
条件
结论
已知事项
由已知事项推断
出的事项
以上命题都是“如果……那么……”的形式;其中“如果”引出的部分是条件,“那么”引出的部分是结论。
命题的结构形式
说出下列命题的条件和结论
1、如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;
2、如果两个三角形中有两边和一个角分别相等,那么这两个三角形全等;
3、如果两个角是内错角,那么它们相等。
尝试练习
命题:对顶角相等.
改写:如果两个角是对顶角,那么这两个角相等。
条件:两个角是对顶角
思考探讨 找出命题的条件和结论:
结论:这两个角相等
有些命题没有写成“如果……那么……”的形式,
条件和结论不明显,经过分析将它们改写成
“如果……那么……”的形式,更容易找出条件和结论。
牛刀小试
将下列命题写成“如果……那么……”的形式,分别指出它的条件和结论。
(1)在同一平面内,垂直于同一直线的两条直线平行;
(2)两个锐角的和是钝角;
(3)负数小于0;
(4)同旁内角互补,两直线平行;
解:(5)改写:如果两个三角形全等,那么这两个三角形的面积相等。
条件:两个三角形全等
结论:这两个三角形的面积相等
解:(1)条件:两个角相等
结论:它们是对顶角
解:(2)条件: a>b,b>c
结论: a=c
解:(3)改写:如果两个三角形的两角和其中一角的对边对应相等,那么这两个三角形全等。
条件:两个三角形的两角和其中一角的对边对应相等
结论:这两个三角形全等
解:(4)改写:如果一个四边形是菱形,那么这个四边形的四条边相等 。
条件:一个四边形是菱形
结论:这个四边形的四条边相等
下列命题的条件是什么?结论是什么?
(1)如果两个角相等,那么它们是对顶角;
(2)如果a>b,b>c,那么a = c;
(3)两角和其中一角的对边对应相等的两个三角形全等;
(4)菱形的四条边都相等;
(5)全等三角形的面积相等。
命题的分类
(1)如果两个角相等,那么它们是对顶角;
(2)直角三角形一定不是轴对称图形;
(3)同角的补角相等。
(4)全等三角形的面积相等。
假命题
假命题
真命题
真命题
说明假命题的方法:
举反例
使之具有命题的条件,而不具有命题的结论。
下面几个命题哪些是正确的?哪些是不正确的?
你如何确定它们是不正确的?
下列命题是真命题还是假命题?如果是假命题,
举出一个反例.
(1)绝对值相等的两个数相等;
(2)内错角相等;
(3)如果a为实数,那么|a|>0;
(4)如果a>b,b>c,那么a>c。
假命题
假命题
真命题
假命题
说出下列命题的条件和结论,并判断它们是真命题还是假命题。
1、如果ab>0,那么a>0,b>0。
2、如果一个三角形中有两个角相等,那么这个三 角形是等腰三角形。
3 、直角三角形的两个锐角互余。
综合提升
假命题
真命题
真命题
条件:ab>0 结论:a>0,b>0
条件:一个三角形中有两个角相等
结论:这个三角形是等腰三角形
条件:一个三角形是直角三角形
结论:它的两个锐角互余
拓展延伸
1.下列命题中,是真命题的是
A 任何数的平方都是正数
B 相等的角是对顶角
C 内错角相等
D 直角都相等
2 .下列命题是假命题的是
A 对顶角相等
B -4是有理数
C 若a2>b2,则a>b
D 三角形内角和是180°
D
C
拓展延伸
3、如图,给出下列论断:(1)AB∥DC;
(2)AD∥BC;(3)∠A=∠C。
选择其中两个论断作为条件,另一个作为结论,用“如果… …那么… …”的形式,构造一个真命题。
解:如果AB∥DC,AD∥BC,那么∠A=∠C。
1、命题的结构:条件和结论
2、命题的形式:“如果……那么……”
3、命题的分类:真命题和假命题
4、说明一个命题是假命题的方法:
举反例
条件
结论
8.1 定义与命题
第2课时 定义与命题(2)
第八章 平行线的有关证明
8.1 定义与命题
第2课时 定义与命题(2)
下列句子是不是命题
(1)如果a=b,那么a+c=b+c;
(2)作线段AB = CD;
(3)三个角对应相等的两个三角形一定全等;
(4)负数都小于零;
(5) ∠A = 90°吗?
是
不是
是
是
不是
8.1 定义与命题
第2课时 定义与命题(2)
合作学习: 观察下列命题,思考:这些命题有什么共同的形式?对于每一个命题,都由几部分组成?分别是哪几部分?
1、如果两个三角形的三条边对应相等,
那么这两个三角形全等;
2、如果a=b,那么a2=b2;
3、如果一个三角形是等腰三角形,
那么这个三角形的两个底角相等;
4、如果两个三角形中有两边和一个角分别相等,
那么这两个三角形全等;
5、如果两个角是内错角,那么它们相等。
8.1 定义与命题
第2课时 定义与命题(2)
如果两个三角形的三条边对应相等,那么这两个三角形全等;
条件
结论
已知事项
由已知事项推断
出的事项
以上命题都是“如果……那么……”的形式;其中“如果”引出的部分是条件,“那么”引出的部分是结论。
命题的结构形式
说出下列命题的条件和结论
1、如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;
2、如果两个三角形中有两边和一个角分别相等,那么这两个三角形全等;
3、如果两个角是内错角,那么它们相等。
尝试练习
命题:对顶角相等.
改写:如果两个角是对顶角,那么这两个角相等。
条件:两个角是对顶角
思考探讨 找出命题的条件和结论:
结论:这两个角相等
有些命题没有写成“如果……那么……”的形式,
条件和结论不明显,经过分析将它们改写成
“如果……那么……”的形式,更容易找出条件和结论。
牛刀小试
将下列命题写成“如果……那么……”的形式,分别指出它的条件和结论。
(1)在同一平面内,垂直于同一直线的两条直线平行;
(2)两个锐角的和是钝角;
(3)负数小于0;
(4)同旁内角互补,两直线平行;
解:(5)改写:如果两个三角形全等,那么这两个三角形的面积相等。
条件:两个三角形全等
结论:这两个三角形的面积相等
解:(1)条件:两个角相等
结论:它们是对顶角
解:(2)条件: a>b,b>c
结论: a=c
解:(3)改写:如果两个三角形的两角和其中一角的对边对应相等,那么这两个三角形全等。
条件:两个三角形的两角和其中一角的对边对应相等
结论:这两个三角形全等
解:(4)改写:如果一个四边形是菱形,那么这个四边形的四条边相等 。
条件:一个四边形是菱形
结论:这个四边形的四条边相等
下列命题的条件是什么?结论是什么?
(1)如果两个角相等,那么它们是对顶角;
(2)如果a>b,b>c,那么a = c;
(3)两角和其中一角的对边对应相等的两个三角形全等;
(4)菱形的四条边都相等;
(5)全等三角形的面积相等。
命题的分类
(1)如果两个角相等,那么它们是对顶角;
(2)直角三角形一定不是轴对称图形;
(3)同角的补角相等。
(4)全等三角形的面积相等。
假命题
假命题
真命题
真命题
说明假命题的方法:
举反例
使之具有命题的条件,而不具有命题的结论。
下面几个命题哪些是正确的?哪些是不正确的?
你如何确定它们是不正确的?
下列命题是真命题还是假命题?如果是假命题,
举出一个反例.
(1)绝对值相等的两个数相等;
(2)内错角相等;
(3)如果a为实数,那么|a|>0;
(4)如果a>b,b>c,那么a>c。
假命题
假命题
真命题
假命题
说出下列命题的条件和结论,并判断它们是真命题还是假命题。
1、如果ab>0,那么a>0,b>0。
2、如果一个三角形中有两个角相等,那么这个三 角形是等腰三角形。
3 、直角三角形的两个锐角互余。
综合提升
假命题
真命题
真命题
条件:ab>0 结论:a>0,b>0
条件:一个三角形中有两个角相等
结论:这个三角形是等腰三角形
条件:一个三角形是直角三角形
结论:它的两个锐角互余
拓展延伸
1.下列命题中,是真命题的是
A 任何数的平方都是正数
B 相等的角是对顶角
C 内错角相等
D 直角都相等
2 .下列命题是假命题的是
A 对顶角相等
B -4是有理数
C 若a2>b2,则a>b
D 三角形内角和是180°
D
C
拓展延伸
3、如图,给出下列论断:(1)AB∥DC;
(2)AD∥BC;(3)∠A=∠C。
选择其中两个论断作为条件,另一个作为结论,用“如果… …那么… …”的形式,构造一个真命题。
解:如果AB∥DC,AD∥BC,那么∠A=∠C。
1、命题的结构:条件和结论
2、命题的形式:“如果……那么……”
3、命题的分类:真命题和假命题
4、说明一个命题是假命题的方法:
举反例
条件
结论
8.1 定义与命题
第2课时 定义与命题(2)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
