鲁教版七年级数学下册8.2证明的必要性课件(共13张PPT)
文档属性
| 名称 | 鲁教版七年级数学下册8.2证明的必要性课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 293.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 11:48:21 | ||
图片预览




文档简介
(共13张PPT)
第八章 平行线的有关证明
8.2 证明的必要性
8.2 证明的必要性
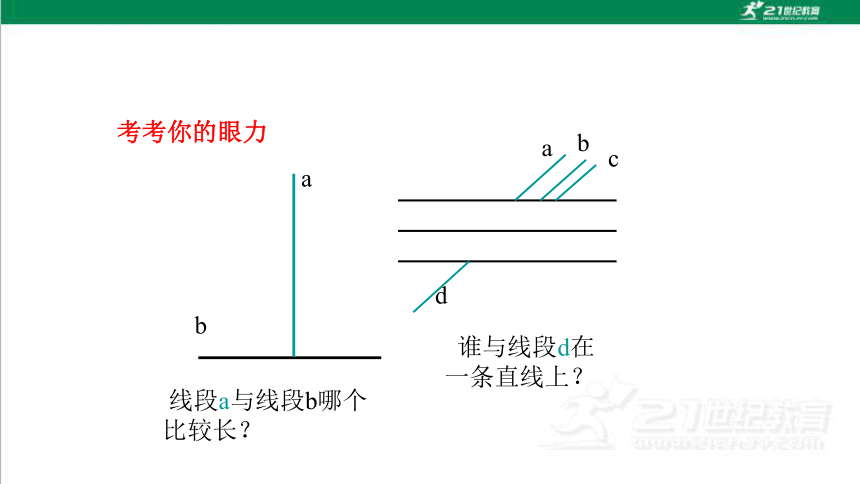
a
b
线段a与线段b哪个
比较长?
a
b
c
d
谁与线段d在
一条直线上?
考考你的眼力
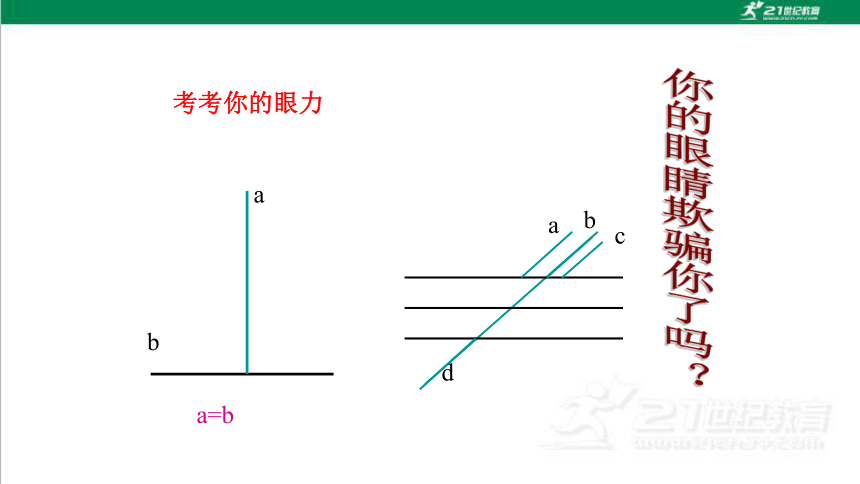
a
b
a
b
c
d
a=b
考考你的眼力
8.2 证明的必要性
创设情境,提出问题
小明任意画了几个三角形,用量角器分别测量各三角形内角的度数,然后把三个角度加起来,发现每个三角形的内角的和都是180度.
于是他就得出了一个一般性的结论:
三角形的三个内角的和等于180度。
小颖对小明的做法提出了异议:你怎么知道你的结论一定可靠呢?三角形有无数个,你才测量了几个三角形?即使测量几千个、几万个,也只是很小的一部分,怎么能从这很小的一部分的性质推出所有三角形的性质呢?
再说,你的测量不可能没有误差,你怎么能确定三角形的内角和正好是180度,而不是181度或179度呢?
设置问题,步步引入
在数学学习中,我们可以通过实验、归纳、观察、猜测等方法,得到数学命题,你是否想过,通过这些方法得到的命题一定是真命题吗?
费 马
对于所有自然数n, 的值都是质数.
当n=0,1,2,3,4时,
= 3,5,17,257,65537
都是质数
欧 拉
当n=5时,
= 4294967297=641×6700417
举出反例是检验错误数学结论的有效方法.
大数学家也有失误
有人认为,对于所有自然数n,代数式n2-n+11的值都是质数.
你怎么看待这个结论?
寻找质数
当n=0,1,2,3,4,5时,代数式n2-n+11的值是质数还是合数?
对于所有自然数n,代数式n2-n+11的值都是质数吗?
做一做
切忌以偏带全,以点带面
如图,四边形ABCD四边的中点分别为F,G,H,E,度量四边形EFGH的边和角,你能发现什么结论?改变四边形ABCD的形状,还能得到类似的结论吗?你能肯定这个结论对所有的四边形ABCD都成立吗?与同伴交流。
做一做
结论
要判断一个命题是不是真命题,仅仅依靠经验、观察、实验和猜想是不够的,必须一步一步、有根有据地进行推理,推理的过程就是证明。
1.在数学学习中,你用过推理吗?举例说明.
2.在日常生活中,你用过推理吗?举例说明.
议一议
(1)读一读孔子与弟子颜回的故事<<知人不易>>
(2)习题8.3
作业
颜回是孔子最得意的门生,有一次孔子周游列国,困于陈蔡之间七天没饭吃,颜回好不容易找到一点粮食,便赶紧埋锅造饭,米饭将熟之际,孔子闻香抬头,恰好看到颜回用手抓出一把米饭送入口中;等到颜回请孔子吃饭,孔子假装说:“我刚刚梦到我父亲,想用这干净的白饭来祭拜他.”颜回赶快接着说:“不行,不行,这饭不干净,刚刚烧饭时有些烟尘掉入锅中,弃之可惜,我便抓出来吃掉了.”孔子这才知道颜回并非偷吃饭,心中相当感慨,便对弟子说:“所信者目也,而且犹不可信;所恃者心也,而心犹不足恃.弟子记之,知人固不易矣!”
第八章 平行线的有关证明
8.2 证明的必要性
8.2 证明的必要性
a
b
线段a与线段b哪个
比较长?
a
b
c
d
谁与线段d在
一条直线上?
考考你的眼力
a
b
a
b
c
d
a=b
考考你的眼力
8.2 证明的必要性
创设情境,提出问题
小明任意画了几个三角形,用量角器分别测量各三角形内角的度数,然后把三个角度加起来,发现每个三角形的内角的和都是180度.
于是他就得出了一个一般性的结论:
三角形的三个内角的和等于180度。
小颖对小明的做法提出了异议:你怎么知道你的结论一定可靠呢?三角形有无数个,你才测量了几个三角形?即使测量几千个、几万个,也只是很小的一部分,怎么能从这很小的一部分的性质推出所有三角形的性质呢?
再说,你的测量不可能没有误差,你怎么能确定三角形的内角和正好是180度,而不是181度或179度呢?
设置问题,步步引入
在数学学习中,我们可以通过实验、归纳、观察、猜测等方法,得到数学命题,你是否想过,通过这些方法得到的命题一定是真命题吗?
费 马
对于所有自然数n, 的值都是质数.
当n=0,1,2,3,4时,
= 3,5,17,257,65537
都是质数
欧 拉
当n=5时,
= 4294967297=641×6700417
举出反例是检验错误数学结论的有效方法.
大数学家也有失误
有人认为,对于所有自然数n,代数式n2-n+11的值都是质数.
你怎么看待这个结论?
寻找质数
当n=0,1,2,3,4,5时,代数式n2-n+11的值是质数还是合数?
对于所有自然数n,代数式n2-n+11的值都是质数吗?
做一做
切忌以偏带全,以点带面
如图,四边形ABCD四边的中点分别为F,G,H,E,度量四边形EFGH的边和角,你能发现什么结论?改变四边形ABCD的形状,还能得到类似的结论吗?你能肯定这个结论对所有的四边形ABCD都成立吗?与同伴交流。
做一做
结论
要判断一个命题是不是真命题,仅仅依靠经验、观察、实验和猜想是不够的,必须一步一步、有根有据地进行推理,推理的过程就是证明。
1.在数学学习中,你用过推理吗?举例说明.
2.在日常生活中,你用过推理吗?举例说明.
议一议
(1)读一读孔子与弟子颜回的故事<<知人不易>>
(2)习题8.3
作业
颜回是孔子最得意的门生,有一次孔子周游列国,困于陈蔡之间七天没饭吃,颜回好不容易找到一点粮食,便赶紧埋锅造饭,米饭将熟之际,孔子闻香抬头,恰好看到颜回用手抓出一把米饭送入口中;等到颜回请孔子吃饭,孔子假装说:“我刚刚梦到我父亲,想用这干净的白饭来祭拜他.”颜回赶快接着说:“不行,不行,这饭不干净,刚刚烧饭时有些烟尘掉入锅中,弃之可惜,我便抓出来吃掉了.”孔子这才知道颜回并非偷吃饭,心中相当感慨,便对弟子说:“所信者目也,而且犹不可信;所恃者心也,而心犹不足恃.弟子记之,知人固不易矣!”
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
