8.6三角形内角和定理第1课时三角形内角和定理(1)课件(共17张PPT)
文档属性
| 名称 | 8.6三角形内角和定理第1课时三角形内角和定理(1)课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 555.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 11:50:08 | ||
图片预览


文档简介
(共17张PPT)
第八章 平行线的有关证明
8.6 三角形内角和定理
第1课时 三角形内角和定理(1)
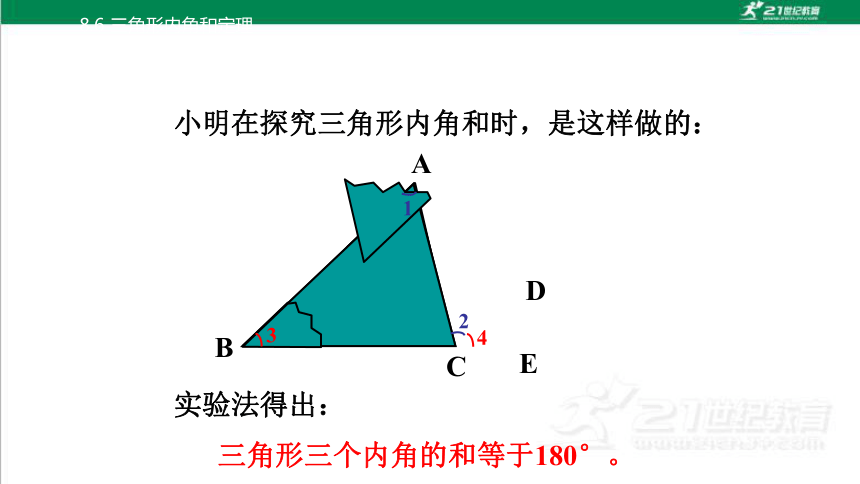
小明在探究三角形内角和时,是这样做的:
A
B
C
3
4
1
2
D
E
实验法得出:
三角形三个内角的和等于180°。
8.6 三角形内角和定理
第1课时 三角形内角和定理(1)
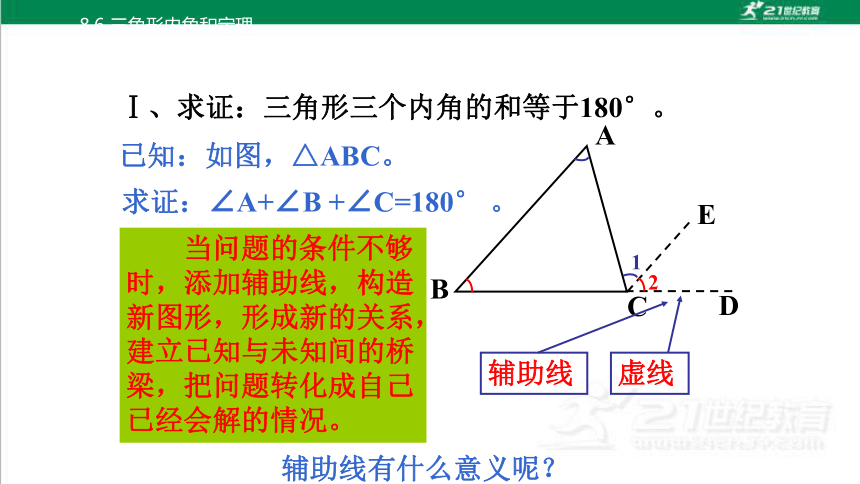
Ⅰ、求证:三角形三个内角的和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
A
B
C
D
E
辅助线
辅助线有什么意义呢?
虚线
1
2
当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。
8.6 三角形内角和定理
第1课时 三角形内角和定理(1)
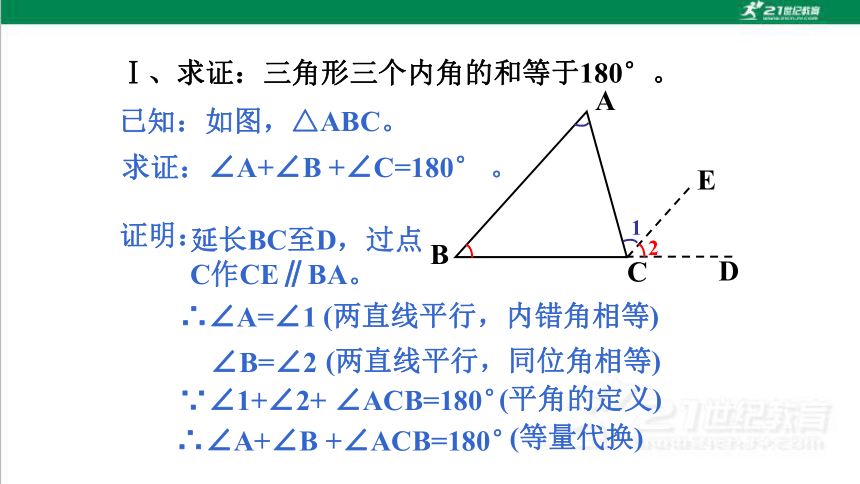
Ⅰ、求证:三角形三个内角的和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
证明:
∴∠A=∠1
(两直线平行,内错角相等)
延长BC至D,过点
C作CE∥BA。
∵∠1+∠2+ ∠ACB=180°
(平角的定义)
∴∠A+∠B +∠ACB=180°
(等量代换)
A
B
C
∠B=∠2
(两直线平行,同位角相等)
D
E
1
2
新知归纳
三角形内角和定理:
三角形三个内角的和等于180°。
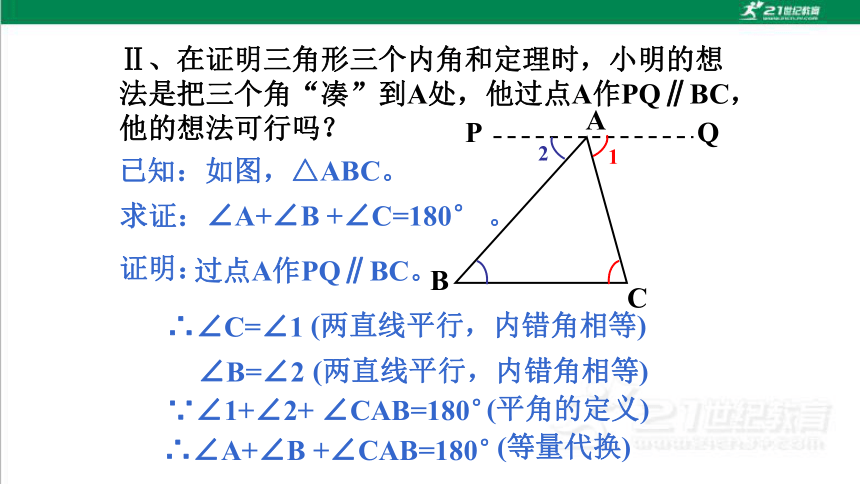
Ⅱ、在证明三角形三个内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作PQ∥BC,
他的想法可行吗?
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
证明:
∴∠C=∠1
(两直线平行,内错角相等)
过点A作PQ∥BC。
∵∠1+∠2+ ∠CAB=180°
(平角的定义)
∴∠A+∠B +∠CAB=180°
(等量代换)
A
B
C
∠B=∠2
(两直线平行,内错角相等)
P
Q
2
1
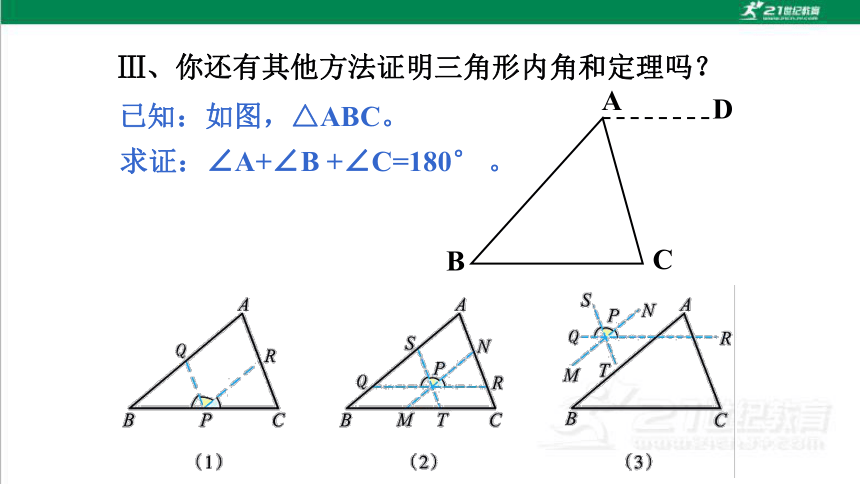
Ⅲ、你还有其他方法证明三角形内角和定理吗?
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
A
B
C
D
1、已知:如图,在△ABC中,∠A=60°,∠C
=70° ,点D和E分别在AB和AC上,且DE∥BC。
求证:∠ADE=50°。
ⅰ、直角三角形的两锐角和是多少度?请证明你
的结论。
A
B
C
已知:如图,Rt△ABC中,∠C=90°。
求证:∠A+∠B =90° 。
证明:
∵∠A+∠B+ ∠C=180°
(三角形三个内角的和等于180°)
且∠C=90°
(已知)
∴∠A+∠B+ 90°=180°
(等量代换)
∴∠A+∠B=90°
(等式性质)
直角三角形两锐角互余
2、已知:如图,在Rt△ABC中,∠ACB=90°,
CD⊥AB,垂足为D。求证:∠A=∠DCB。
ⅱ、正三角形的一个内角是多少度?证明你的结论。
A
B
C
已知:如图,正△ABC。
求证:∠A=∠B=∠C =60° 。
证明:
∵∠A+∠B+ ∠C=180°
(三角形三个内角和等于180°)
∵△ABC是正三角形
(已知)
∴∠A=∠B=∠C
(正三角形性质)
∴∠A=∠B=∠C =60°
(等式性质)
正三角形的三个内角都相等,并且都等于60°
A
B
C
D
已知:如图,四边形ABCD。
求证:∠A+∠B+∠C+∠D=360° 。
证明:
∵∠BAC+∠B+ ∠ACB=180°
(三角形三个内角和等于180°)
连接AC
且∠DAC+∠D+ ∠ACD=180°
(三角形三个内角和等于180°)
∴∠DAB+∠B+∠BCD+∠D =360°
(等式性质)
四边形的内角和等于360°
定理:
(1)直角三角形的两锐角互余;
(2)正三角形的三个内角都相等,且都等于60°;
(3)四边形的内角和等于360°。
3、已知:如图,AB∥CD。求证:∠CAB=
∠CED+∠CDE 。
巩固练习
合作交流
ⅳ、如图(1),在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来接近BC时,∠A就越来越大(越来越接近180°),而∠B和∠C则越来越小(越来越接近0°)。由此你能想到什么?
A
B
C
A
B
C
(1)
(2)
如果BC不动,把点A“拉离”BC,那么当点A越来远离BC时,∠A就越来越小(越来越接近0°),而∠B和∠C则越来越大,它们的和越来越接近180°。当点A拉到无穷远时,便有AB∥AC,而∠B和∠C是同旁内角,此时它们的和等于180°。由此你能想到什么?
4、已知:如图,在△ABC中,∠A=75°,∠B
=50°,将∠C折起,点C落在△ABC内部,已知∠1=20°,求∠2的大小。
巩固练习
1
2
A
B
C
D
E
1、辅助线的意义:
当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。
2、三角形内角和定理:
三角形三个内角的和等于180°。
3、定理:
(1)直角三角形的两锐角互余;
(2)正三角形的三个内角都相等,且都等于60°;
(3)四边形的内角和等于360°。
8.6 三角形内角和定理
第1课时 三角形内角和定理(1)
第八章 平行线的有关证明
8.6 三角形内角和定理
第1课时 三角形内角和定理(1)
小明在探究三角形内角和时,是这样做的:
A
B
C
3
4
1
2
D
E
实验法得出:
三角形三个内角的和等于180°。
8.6 三角形内角和定理
第1课时 三角形内角和定理(1)
Ⅰ、求证:三角形三个内角的和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
A
B
C
D
E
辅助线
辅助线有什么意义呢?
虚线
1
2
当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。
8.6 三角形内角和定理
第1课时 三角形内角和定理(1)
Ⅰ、求证:三角形三个内角的和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
证明:
∴∠A=∠1
(两直线平行,内错角相等)
延长BC至D,过点
C作CE∥BA。
∵∠1+∠2+ ∠ACB=180°
(平角的定义)
∴∠A+∠B +∠ACB=180°
(等量代换)
A
B
C
∠B=∠2
(两直线平行,同位角相等)
D
E
1
2
新知归纳
三角形内角和定理:
三角形三个内角的和等于180°。
Ⅱ、在证明三角形三个内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作PQ∥BC,
他的想法可行吗?
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
证明:
∴∠C=∠1
(两直线平行,内错角相等)
过点A作PQ∥BC。
∵∠1+∠2+ ∠CAB=180°
(平角的定义)
∴∠A+∠B +∠CAB=180°
(等量代换)
A
B
C
∠B=∠2
(两直线平行,内错角相等)
P
Q
2
1
Ⅲ、你还有其他方法证明三角形内角和定理吗?
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
A
B
C
D
1、已知:如图,在△ABC中,∠A=60°,∠C
=70° ,点D和E分别在AB和AC上,且DE∥BC。
求证:∠ADE=50°。
ⅰ、直角三角形的两锐角和是多少度?请证明你
的结论。
A
B
C
已知:如图,Rt△ABC中,∠C=90°。
求证:∠A+∠B =90° 。
证明:
∵∠A+∠B+ ∠C=180°
(三角形三个内角的和等于180°)
且∠C=90°
(已知)
∴∠A+∠B+ 90°=180°
(等量代换)
∴∠A+∠B=90°
(等式性质)
直角三角形两锐角互余
2、已知:如图,在Rt△ABC中,∠ACB=90°,
CD⊥AB,垂足为D。求证:∠A=∠DCB。
ⅱ、正三角形的一个内角是多少度?证明你的结论。
A
B
C
已知:如图,正△ABC。
求证:∠A=∠B=∠C =60° 。
证明:
∵∠A+∠B+ ∠C=180°
(三角形三个内角和等于180°)
∵△ABC是正三角形
(已知)
∴∠A=∠B=∠C
(正三角形性质)
∴∠A=∠B=∠C =60°
(等式性质)
正三角形的三个内角都相等,并且都等于60°
A
B
C
D
已知:如图,四边形ABCD。
求证:∠A+∠B+∠C+∠D=360° 。
证明:
∵∠BAC+∠B+ ∠ACB=180°
(三角形三个内角和等于180°)
连接AC
且∠DAC+∠D+ ∠ACD=180°
(三角形三个内角和等于180°)
∴∠DAB+∠B+∠BCD+∠D =360°
(等式性质)
四边形的内角和等于360°
定理:
(1)直角三角形的两锐角互余;
(2)正三角形的三个内角都相等,且都等于60°;
(3)四边形的内角和等于360°。
3、已知:如图,AB∥CD。求证:∠CAB=
∠CED+∠CDE 。
巩固练习
合作交流
ⅳ、如图(1),在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来接近BC时,∠A就越来越大(越来越接近180°),而∠B和∠C则越来越小(越来越接近0°)。由此你能想到什么?
A
B
C
A
B
C
(1)
(2)
如果BC不动,把点A“拉离”BC,那么当点A越来远离BC时,∠A就越来越小(越来越接近0°),而∠B和∠C则越来越大,它们的和越来越接近180°。当点A拉到无穷远时,便有AB∥AC,而∠B和∠C是同旁内角,此时它们的和等于180°。由此你能想到什么?
4、已知:如图,在△ABC中,∠A=75°,∠B
=50°,将∠C折起,点C落在△ABC内部,已知∠1=20°,求∠2的大小。
巩固练习
1
2
A
B
C
D
E
1、辅助线的意义:
当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。
2、三角形内角和定理:
三角形三个内角的和等于180°。
3、定理:
(1)直角三角形的两锐角互余;
(2)正三角形的三个内角都相等,且都等于60°;
(3)四边形的内角和等于360°。
8.6 三角形内角和定理
第1课时 三角形内角和定理(1)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
