8.6三角形内角和定理第2课时三角形内角和定理(2)课件(共11张PPT)
文档属性
| 名称 | 8.6三角形内角和定理第2课时三角形内角和定理(2)课件(共11张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 341.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 11:50:59 | ||
图片预览


文档简介
(共11张PPT)
第八章 平行线的有关证明
8.6 三角形内角和定理
第2课时 三角形内角和定理(2)
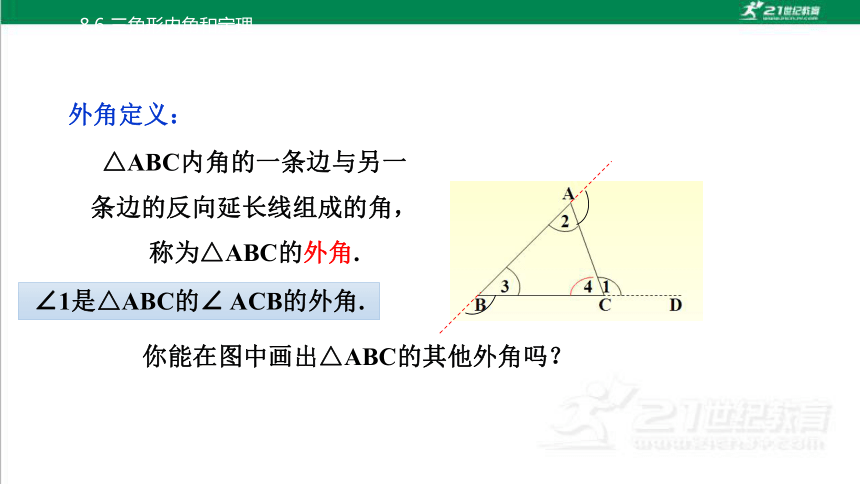
外角定义:
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC的外角.
∠1是△ABC的∠ ACB的外角.
你能在图中画出△ABC的其他外角吗?
8.6 三角形内角和定理
第2课时 三角形内角和定理(2)
如图. ∠1是△ABC的一个外角, ∠1与图中的其他角有什么关系
∠1+∠4=180°;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3.
证明:∵∠2+∠3+∠4=180°(三角形内角和定理),
∠1+∠4=180°(平角的意义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
A
B
C
D
1
2
3
4
能证明你的结论吗
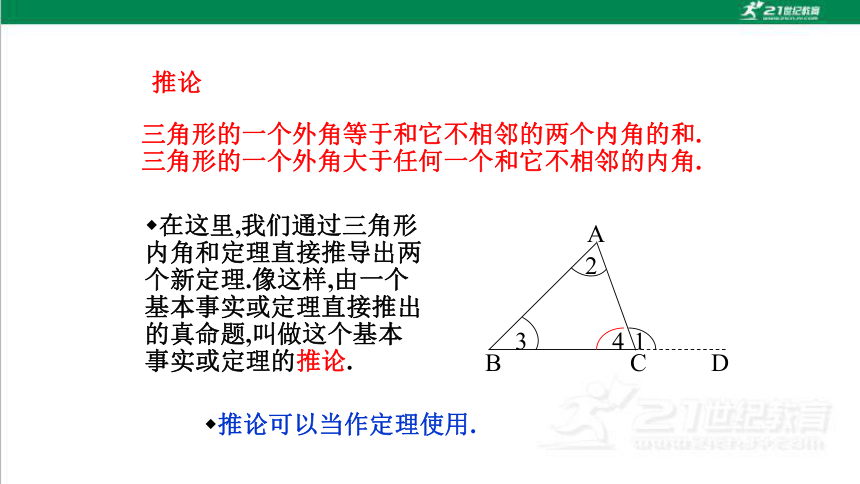
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
议一议
8.6 三角形内角和定理
第2课时 三角形内角和定理(2)
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
1
2
3
4
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个基本事实或定理直接推出的真命题,叫做这个基本事实或定理的推论.
推论可以当作定理使用.
推论
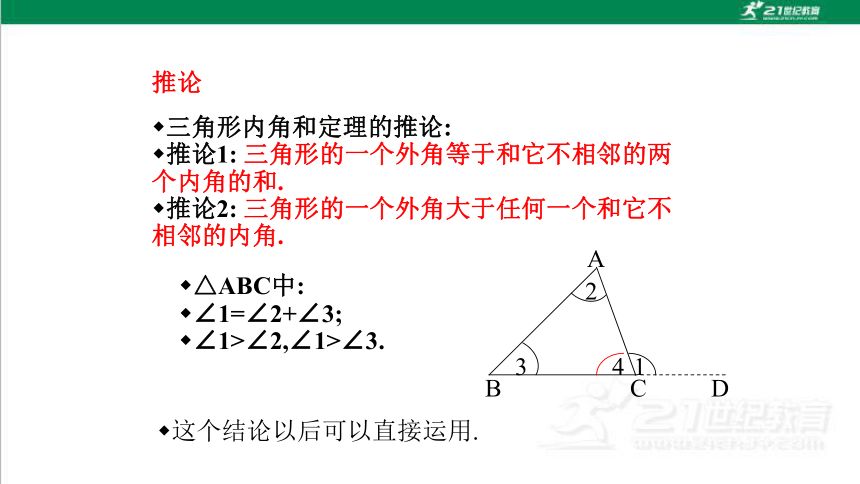
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3.
A
B
C
D
1
2
3
4
这个结论以后可以直接运用.
推论
例2 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
∴ AD∥BC(内错角相等,两直线平行).
∠B=∠C (已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
∵ AD平分 ∠EAC(已知).
∴∠C= ∠EAC(等式性质).
∴∠DAC= ∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证实.
还有其他方法吗?
方法一
应用
A
C
D
B
E
·
·
例2 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
∠B=∠C (已知),
∴∠B= ∠EAC(等式性质).
∵ AD平分 ∠EAC(已知).
∴∠DAE= ∠EAC(角平分线的定义).
∴∠DAE=∠B(等量代换).
∴ AD∥BC(同位角相等,两直线平行).
这里是运用了公理“同位角相等,两直线平行”得到了证实.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
方法二
应用
A
C
D
B
E
·
例2 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
∠DAC=∠C (已证),
∵ ∠BAC+∠B+∠C =180° (三角形内角和定理).
∴ ∠BAC+∠B+∠DAC =180° (等量代换).
∴ a∥b(同旁内角互补,两直线平行).
这里是运用了定理“同旁内角互补,两直线平行”得到了证实.
证明:由证法1可得:
·
方法三
应用
例3 已知:如图, ∠BAF, ∠CBD, ∠ACE是△ABC的三个外角。
求证: ∠BAF+∠CBD+∠ACE=360°.
B
A
C
D
F
E
1
2
3
证明:∵ ∠BAF是△ABC的一个外角(已知)
∴ ∠BAF=∠2+∠3 (三角形的一个外角等于和它不相邻的两个内角的和).
同理,∠CBD=∠1+∠3 , ∠ACE= ∠1+∠2.
∴ ∠BAF+∠CBD+∠ACE=2× 180°= 360°(等量代换)
∵ ( ∠1+∠2 + ∠3)=180°(三角形内角和定理)
∴ ∠BAF+∠CBD+∠ACE=2( ∠1+∠2 + ∠3)(等式的性质)
应用
已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:∵ ∠DCA是△ABC的一个外角(已知),
∠DCA=100°(已知),
∴ ∠B=100°-45°=55°.(三角形的一个外角等于和它不相邻的两个内角的和).
又∵ ∠DCA+∠BCA=180°(平角意义).
∴ ∠ACB=80°(等式的性质).
∠A=45°(已知),
随堂练习
三角形内角和定理 :
三角形三个内角的和等于180°。
推论1:
三角形的一个外角等于和它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个和它不相邻的内角.
推论3:
直角三角形的两锐角互余.
8.6 三角形内角和定理
第2课时 三角形内角和定理(2)
第八章 平行线的有关证明
8.6 三角形内角和定理
第2课时 三角形内角和定理(2)
外角定义:
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC的外角.
∠1是△ABC的∠ ACB的外角.
你能在图中画出△ABC的其他外角吗?
8.6 三角形内角和定理
第2课时 三角形内角和定理(2)
如图. ∠1是△ABC的一个外角, ∠1与图中的其他角有什么关系
∠1+∠4=180°;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3.
证明:∵∠2+∠3+∠4=180°(三角形内角和定理),
∠1+∠4=180°(平角的意义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
A
B
C
D
1
2
3
4
能证明你的结论吗
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
议一议
8.6 三角形内角和定理
第2课时 三角形内角和定理(2)
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
1
2
3
4
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个基本事实或定理直接推出的真命题,叫做这个基本事实或定理的推论.
推论可以当作定理使用.
推论
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3.
A
B
C
D
1
2
3
4
这个结论以后可以直接运用.
推论
例2 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
∴ AD∥BC(内错角相等,两直线平行).
∠B=∠C (已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
∵ AD平分 ∠EAC(已知).
∴∠C= ∠EAC(等式性质).
∴∠DAC= ∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证实.
还有其他方法吗?
方法一
应用
A
C
D
B
E
·
·
例2 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
∠B=∠C (已知),
∴∠B= ∠EAC(等式性质).
∵ AD平分 ∠EAC(已知).
∴∠DAE= ∠EAC(角平分线的定义).
∴∠DAE=∠B(等量代换).
∴ AD∥BC(同位角相等,两直线平行).
这里是运用了公理“同位角相等,两直线平行”得到了证实.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
方法二
应用
A
C
D
B
E
·
例2 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C.
求证:AD∥BC.
∠DAC=∠C (已证),
∵ ∠BAC+∠B+∠C =180° (三角形内角和定理).
∴ ∠BAC+∠B+∠DAC =180° (等量代换).
∴ a∥b(同旁内角互补,两直线平行).
这里是运用了定理“同旁内角互补,两直线平行”得到了证实.
证明:由证法1可得:
·
方法三
应用
例3 已知:如图, ∠BAF, ∠CBD, ∠ACE是△ABC的三个外角。
求证: ∠BAF+∠CBD+∠ACE=360°.
B
A
C
D
F
E
1
2
3
证明:∵ ∠BAF是△ABC的一个外角(已知)
∴ ∠BAF=∠2+∠3 (三角形的一个外角等于和它不相邻的两个内角的和).
同理,∠CBD=∠1+∠3 , ∠ACE= ∠1+∠2.
∴ ∠BAF+∠CBD+∠ACE=2× 180°= 360°(等量代换)
∵ ( ∠1+∠2 + ∠3)=180°(三角形内角和定理)
∴ ∠BAF+∠CBD+∠ACE=2( ∠1+∠2 + ∠3)(等式的性质)
应用
已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:∵ ∠DCA是△ABC的一个外角(已知),
∠DCA=100°(已知),
∴ ∠B=100°-45°=55°.(三角形的一个外角等于和它不相邻的两个内角的和).
又∵ ∠DCA+∠BCA=180°(平角意义).
∴ ∠ACB=80°(等式的性质).
∠A=45°(已知),
随堂练习
三角形内角和定理 :
三角形三个内角的和等于180°。
推论1:
三角形的一个外角等于和它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个和它不相邻的内角.
推论3:
直角三角形的两锐角互余.
8.6 三角形内角和定理
第2课时 三角形内角和定理(2)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
