10.1全等三角形第3课时全等三角形(3)课件(共16张PPT)
文档属性
| 名称 | 10.1全等三角形第3课时全等三角形(3)课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 12:03:16 | ||
图片预览






文档简介
(共16张PPT)
第十章 三角形的有关证明
10.1 全等三角形
第3课时 全等三角形(3)
上节课我们较熟练地掌握了证明的基本步骤和书写格式,会较灵活地运用判定一般三角形全等的方法,证明三角形全等,并且初步掌握了利用全等三角形证明线段或角相等。
10.1 全等三角形
第3课时 全等三角形(3)
1.掌握全等三角形的判断定理并能正确应用;
2.用分析法寻求证题思路,用综合法书写证明过程.
继续探究
这节课我们来进一步研究全等三角形。
先看一个关于全等三角形的例题:
10.1 全等三角形
第3课时 全等三角形(3)
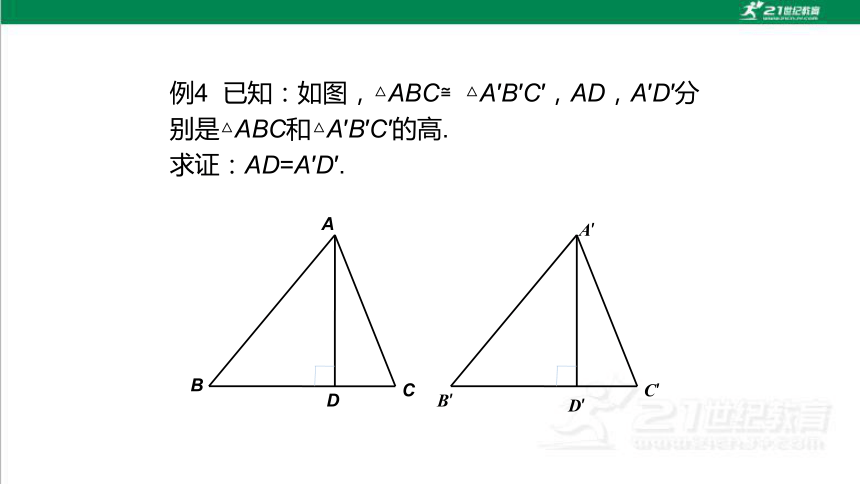
例4 已知:如图,△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高.
求证:AD=A′D′.
A
B
D
C
B′
A′
C′
D′
证明:
∴AD=A′D′(全等三角形的对应边相等).
∴ △ABD≌△A′B′D′(AAS).
∵ ∠ADB =∠A′D′B′=90°,
∠B=∠B′(全等三角形的对应角相等).
∴AB=A′B′(全等三角形的对应边相等) ,
∵ △ABC≌△A′B′C′,
小结
因为△ABC≌△A′B′C′,
可从这两个三角形中,
根据需要选取其中的部分
或全部相等的边或角。
想一想
(1)如果两个全等三角形对应边上的高在三角形的外部,你还能得到上面的结论吗?
(2)如果两个全等三角形对应边上的就是该三角形的一条边呢?
(3)通过例4和上面的两个问题,你能得到什么结论?与同伴进行交流.
能
结论依然成立
全等三角形对应边上的高相等.
结论:全等三角形对应边上的高相等.
既然全等三角形对应边上的高相等,那么,全等三角形对应角的平分线相等吗?
如果相等,你能写出证明过程吗?
典型例题
例5 已知:如图, AB=CD,BE=DF, ∠B=∠D.
求证:(1) AE=CF;
(2) AE∥CF;
(3)∠AFE= ∠CEF.
A
B
F
E
C
D
要证明两条线段(或两个角)相等,可以通过这两条线段(或两个角)所在的两个三角形全等来证明.
证明:
∴AE=CF(全等三角形的对应边相等).
∴ △ABE≌△CDF(SAS).
∵AB=CD,∠B=∠D, BE=DF,
(1)在△ABE和△CDF中,
(2) ∵ △ABE≌△CDF,
∴ ∠AEB= ∠CFD(全等三角形的对应角相等).
∴ AE∥CF.
A
B
F
E
C
D
∴ ∠AFE= ∠CEF(全等三角形的对应角相等).
∴ △AEF≌△CFE(SAS).
∵AE=CF,∠AEF= ∠CFE,EF=FE,
(3)在△AEF和△CFE中,
A
B
F
E
C
D
1.如图,△ABD≌△AEC,∠B 与∠E是对应角, AB与AE是对应边,BC与ED相等吗?为什么?
B
C
E
D
A
解:相等。理由如下:
∵△ABD≌△AEC,
∴BD=EC .
∴ BD–DC=EC–DC,
即 BC=ED.
F
E
G
H
N
M
2.如图,△EFG≌ △NMH.在△EFG中,FG是最长边.在△NMH中,MH是最长边.∠F和∠M是对应角.EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角,有没有平行线?
(2)求线段NM及HG的长度。
本节课我们通过观察探索、发现并证明了三角形中相等的线段和角,用综合法书写证明过程.
10.1 全等三角形
第3课时 全等三角形(3)
第十章 三角形的有关证明
10.1 全等三角形
第3课时 全等三角形(3)
上节课我们较熟练地掌握了证明的基本步骤和书写格式,会较灵活地运用判定一般三角形全等的方法,证明三角形全等,并且初步掌握了利用全等三角形证明线段或角相等。
10.1 全等三角形
第3课时 全等三角形(3)
1.掌握全等三角形的判断定理并能正确应用;
2.用分析法寻求证题思路,用综合法书写证明过程.
继续探究
这节课我们来进一步研究全等三角形。
先看一个关于全等三角形的例题:
10.1 全等三角形
第3课时 全等三角形(3)
例4 已知:如图,△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高.
求证:AD=A′D′.
A
B
D
C
B′
A′
C′
D′
证明:
∴AD=A′D′(全等三角形的对应边相等).
∴ △ABD≌△A′B′D′(AAS).
∵ ∠ADB =∠A′D′B′=90°,
∠B=∠B′(全等三角形的对应角相等).
∴AB=A′B′(全等三角形的对应边相等) ,
∵ △ABC≌△A′B′C′,
小结
因为△ABC≌△A′B′C′,
可从这两个三角形中,
根据需要选取其中的部分
或全部相等的边或角。
想一想
(1)如果两个全等三角形对应边上的高在三角形的外部,你还能得到上面的结论吗?
(2)如果两个全等三角形对应边上的就是该三角形的一条边呢?
(3)通过例4和上面的两个问题,你能得到什么结论?与同伴进行交流.
能
结论依然成立
全等三角形对应边上的高相等.
结论:全等三角形对应边上的高相等.
既然全等三角形对应边上的高相等,那么,全等三角形对应角的平分线相等吗?
如果相等,你能写出证明过程吗?
典型例题
例5 已知:如图, AB=CD,BE=DF, ∠B=∠D.
求证:(1) AE=CF;
(2) AE∥CF;
(3)∠AFE= ∠CEF.
A
B
F
E
C
D
要证明两条线段(或两个角)相等,可以通过这两条线段(或两个角)所在的两个三角形全等来证明.
证明:
∴AE=CF(全等三角形的对应边相等).
∴ △ABE≌△CDF(SAS).
∵AB=CD,∠B=∠D, BE=DF,
(1)在△ABE和△CDF中,
(2) ∵ △ABE≌△CDF,
∴ ∠AEB= ∠CFD(全等三角形的对应角相等).
∴ AE∥CF.
A
B
F
E
C
D
∴ ∠AFE= ∠CEF(全等三角形的对应角相等).
∴ △AEF≌△CFE(SAS).
∵AE=CF,∠AEF= ∠CFE,EF=FE,
(3)在△AEF和△CFE中,
A
B
F
E
C
D
1.如图,△ABD≌△AEC,∠B 与∠E是对应角, AB与AE是对应边,BC与ED相等吗?为什么?
B
C
E
D
A
解:相等。理由如下:
∵△ABD≌△AEC,
∴BD=EC .
∴ BD–DC=EC–DC,
即 BC=ED.
F
E
G
H
N
M
2.如图,△EFG≌ △NMH.在△EFG中,FG是最长边.在△NMH中,MH是最长边.∠F和∠M是对应角.EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角,有没有平行线?
(2)求线段NM及HG的长度。
本节课我们通过观察探索、发现并证明了三角形中相等的线段和角,用综合法书写证明过程.
10.1 全等三角形
第3课时 全等三角形(3)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
