10.1全等三角形第1课时全等三角形(1)课件(共17张PPT)
文档属性
| 名称 | 10.1全等三角形第1课时全等三角形(1)课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 12:02:30 | ||
图片预览




文档简介
(共17张PPT)
第十章 三角形的有关证明
10.1 全等三角形
第1课时 全等三角形(1)
我们曾经探索过等腰三角形和直角三角形的一些性质,如等腰三角形“三线合一”的性质、勾股定理等.你还记得获得这些结论的过程吗?你能根据已有基本事实和定理证明这些结论吗?
10.1 全等三角形
第1课时 全等三角形(1)
在《平行线的有关证明》一章中,我们给出了八条基本事实,并从其中几条基本事实出发证明了有关平行线的一些结论.运用这些基本事实和已经学习过的定理,我们还可以证明与三角形有关的一些结论.
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知)和结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
与同伴交流你在探索思路过程中的具体做法.
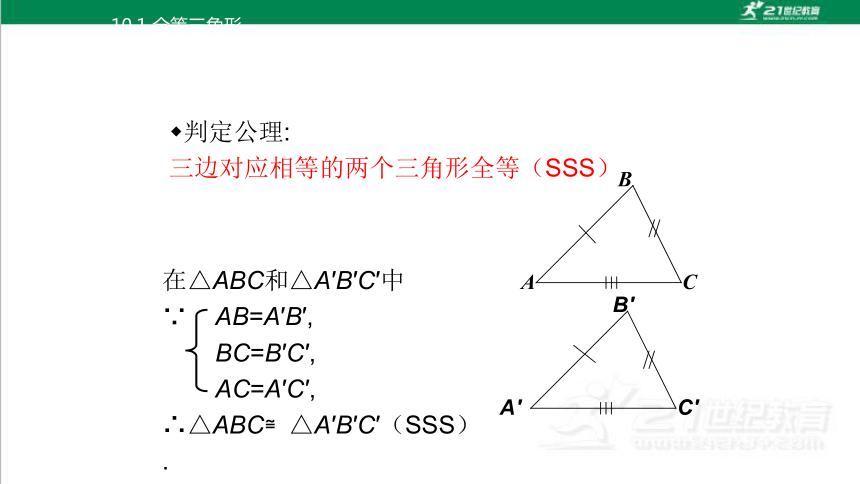
判定公理:
三边对应相等的两个三角形全等(SSS).
A
B
C
A′
B′
C′
在△ABC和△A′B′C′中
∵ AB=A′B′,
BC=B′C′,
AC=A′C′,
∴△ABC≌△A′B′C′(SSS).
10.1 全等三角形
第1课时 全等三角形(1)
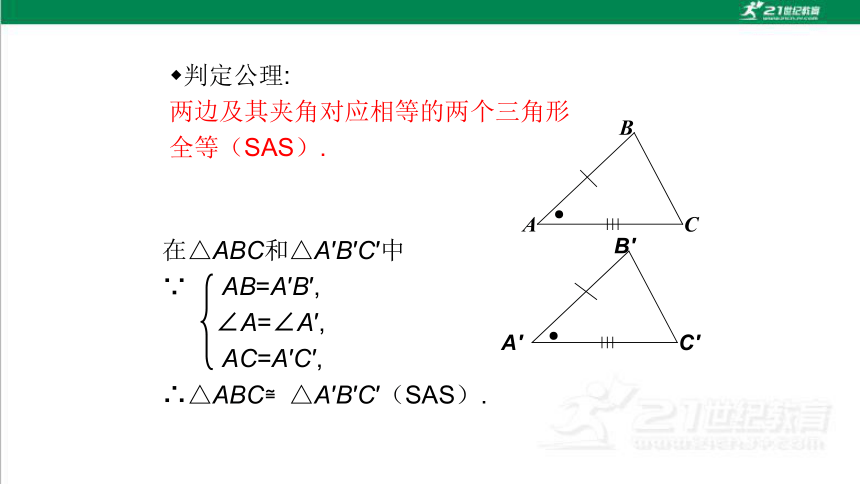
判定公理:
两边及其夹角对应相等的两个三角形全等(SAS).
在△ABC和△A′B′C′中
∵ AB=A′B′,
∠A=∠A′,
AC=A′C′,
∴△ABC≌△A′B′C′(SAS).
A
B
C
A′
B′
C′
●
●
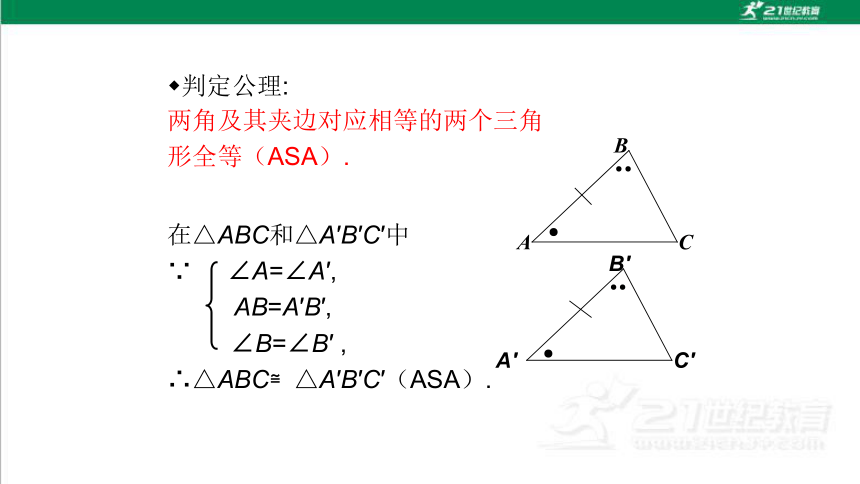
判定公理:
两角及其夹边对应相等的两个三角形全等(ASA).
在△ABC和△A′B′C′中
∵ ∠A=∠A′,
AB=A′B′,
∠B=∠B′ ,
∴△ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
●
●
● ●
● ●
性质公理:
全等三角形的对应边相等、对应角相等.
∵ △ABC≌△A′B′C′,
∴ AB=A′B′,BC=B′C′,AC=A′C′
(全等三角形的对应边相等);
∠A=∠A′,∠B=∠B′,∠C=∠C′
(全等三角形的对应角相等).
●
●
● ●
● ●
A
B
C
A′
B′
C′
● ● ●
● ● ●
1.了解作为证明基础的几条公理的内容;
2.掌握证明的基本步骤和书写格式.
我们已经探索过“两角分别相等且其中一组等角的对边相等的两个三角形全等”这个结论,你能用有关的基本事实和已经证明过的定理证明它吗?
做一做
推论
两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
用心想一想,马到功成
已知:如图,∠B=∠B′,∠C=∠C′,AB=A′B′.
求证:△ABC≌△A′B′C′.
C
B
A
A′
B′
C′
推论
两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
证明:
∵∠A+∠B+∠C=180°,
∠A′+∠B′+∠C′=180°(三角形内角和等于180°),
∴∠A=180°-(∠B+∠C),
∠A′=180°-(∠B′+∠C′).
∵ ∠B=∠B′,∠C=∠C′(已知),
∴∠A=∠A′(等量代换).
∵∠A=∠A′,AB=A′B′,∠B=∠B′,
∴△ABC≌△A′B′C′(ASA).
C
B
A
A′
B′
C′
几何的三种语言
推论:
两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
在△ABC和△A′B′C′中,
∵ ∠A=∠A′,
∠C=∠C′,
AB=A′B′,
∴△ABC≌△A′B′C′(AAS).
证明后的结论,以后可以直接运用.
A
B
C
A′
B′
C′
●
●
● ●
● ●
证明:在△OAC和△ODB中,
∵ OA=OD,
∠AOC= ∠DOB,
OC=OB,
∴△OAC≌△ODB (SAS).
∴ AC=BD,∠A=∠D(全等三角形的定义).
例1 已知:如图,线段AB和CD相交于点O,线段OA=OD,OC=OB.
求证:AC=BD,∠A=∠D.
O
D
A
C
B
根据全等三角形的定义,我们可以得到全等三角形的对应边相等、对应角相等.
小试牛刀
1.完成课本随堂练习第1题,直接做到课本上.
2.已知:如图,M是线段AB的中点,∠C=∠D, ∠1= ∠2.
求证:△AMC ≌△BMD.
A
B
C
D
M
1
2
1.有关全等三角形的基本事实:
SAS,ASA,SSS.
2.判定全等三角形的推论:AAS
两角分别相等且其中一组等角的对边相等的两个三角形全等.
10.1 全等三角形
第1课时 全等三角形(1)
第十章 三角形的有关证明
10.1 全等三角形
第1课时 全等三角形(1)
我们曾经探索过等腰三角形和直角三角形的一些性质,如等腰三角形“三线合一”的性质、勾股定理等.你还记得获得这些结论的过程吗?你能根据已有基本事实和定理证明这些结论吗?
10.1 全等三角形
第1课时 全等三角形(1)
在《平行线的有关证明》一章中,我们给出了八条基本事实,并从其中几条基本事实出发证明了有关平行线的一些结论.运用这些基本事实和已经学习过的定理,我们还可以证明与三角形有关的一些结论.
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知)和结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
与同伴交流你在探索思路过程中的具体做法.
判定公理:
三边对应相等的两个三角形全等(SSS).
A
B
C
A′
B′
C′
在△ABC和△A′B′C′中
∵ AB=A′B′,
BC=B′C′,
AC=A′C′,
∴△ABC≌△A′B′C′(SSS).
10.1 全等三角形
第1课时 全等三角形(1)
判定公理:
两边及其夹角对应相等的两个三角形全等(SAS).
在△ABC和△A′B′C′中
∵ AB=A′B′,
∠A=∠A′,
AC=A′C′,
∴△ABC≌△A′B′C′(SAS).
A
B
C
A′
B′
C′
●
●
判定公理:
两角及其夹边对应相等的两个三角形全等(ASA).
在△ABC和△A′B′C′中
∵ ∠A=∠A′,
AB=A′B′,
∠B=∠B′ ,
∴△ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
●
●
● ●
● ●
性质公理:
全等三角形的对应边相等、对应角相等.
∵ △ABC≌△A′B′C′,
∴ AB=A′B′,BC=B′C′,AC=A′C′
(全等三角形的对应边相等);
∠A=∠A′,∠B=∠B′,∠C=∠C′
(全等三角形的对应角相等).
●
●
● ●
● ●
A
B
C
A′
B′
C′
● ● ●
● ● ●
1.了解作为证明基础的几条公理的内容;
2.掌握证明的基本步骤和书写格式.
我们已经探索过“两角分别相等且其中一组等角的对边相等的两个三角形全等”这个结论,你能用有关的基本事实和已经证明过的定理证明它吗?
做一做
推论
两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
用心想一想,马到功成
已知:如图,∠B=∠B′,∠C=∠C′,AB=A′B′.
求证:△ABC≌△A′B′C′.
C
B
A
A′
B′
C′
推论
两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
证明:
∵∠A+∠B+∠C=180°,
∠A′+∠B′+∠C′=180°(三角形内角和等于180°),
∴∠A=180°-(∠B+∠C),
∠A′=180°-(∠B′+∠C′).
∵ ∠B=∠B′,∠C=∠C′(已知),
∴∠A=∠A′(等量代换).
∵∠A=∠A′,AB=A′B′,∠B=∠B′,
∴△ABC≌△A′B′C′(ASA).
C
B
A
A′
B′
C′
几何的三种语言
推论:
两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
在△ABC和△A′B′C′中,
∵ ∠A=∠A′,
∠C=∠C′,
AB=A′B′,
∴△ABC≌△A′B′C′(AAS).
证明后的结论,以后可以直接运用.
A
B
C
A′
B′
C′
●
●
● ●
● ●
证明:在△OAC和△ODB中,
∵ OA=OD,
∠AOC= ∠DOB,
OC=OB,
∴△OAC≌△ODB (SAS).
∴ AC=BD,∠A=∠D(全等三角形的定义).
例1 已知:如图,线段AB和CD相交于点O,线段OA=OD,OC=OB.
求证:AC=BD,∠A=∠D.
O
D
A
C
B
根据全等三角形的定义,我们可以得到全等三角形的对应边相等、对应角相等.
小试牛刀
1.完成课本随堂练习第1题,直接做到课本上.
2.已知:如图,M是线段AB的中点,∠C=∠D, ∠1= ∠2.
求证:△AMC ≌△BMD.
A
B
C
D
M
1
2
1.有关全等三角形的基本事实:
SAS,ASA,SSS.
2.判定全等三角形的推论:AAS
两角分别相等且其中一组等角的对边相等的两个三角形全等.
10.1 全等三角形
第1课时 全等三角形(1)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
