10.5角平分线第1课时角平分线(1)课件(共18张PPT)
文档属性
| 名称 | 10.5角平分线第1课时角平分线(1)课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 429.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第十章 三角形的有关证明
10.5 角平分线
第1课时 角平分线(1)
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
这个结论是经常用来证明两条线段相等的根据之一.
A
C
B
P
M
N
如图,
∵ AC=BC, MN⊥AB,
P是MN上任意一点(已知),
∴ PA=PB
(线段垂直平分线上的点到这条线段两个端点的距离相等).
10.5 角平分线
第1课时 角平分线(1)
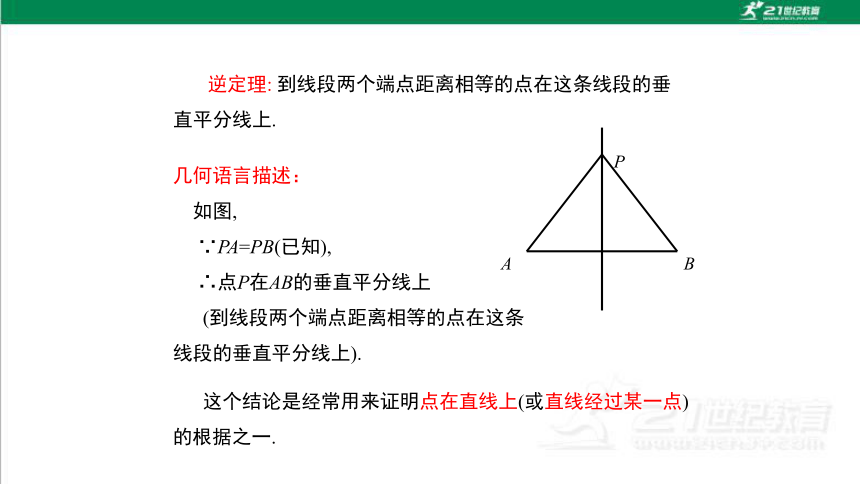
逆定理: 到线段两个端点距离相等的点在这条线段的垂直平分线上.
几何语言描述:
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上
(到线段两个端点距离相等的点在这条线段的垂直平分线上).
这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
A
B
P
那么结合我们前面学习的有关线段垂直平分线的定理及证明方法,你还记得角平分线上的点有什么性质吗
10.5 角平分线
第1课时 角平分线(1)
1.能够证明角平分线的性质定理及其逆定理;
2.进一步发展自己的推理证明意识和能力,培养将文字语言转化为符号语言、图形语言的能力.
你能利用折纸的方法得到角平分线及角平分线上的点的性质吗
你还记得角平分线上的点有什么性质吗
角平分线上的点到这个角的两边的距离相等.
你能证明这一结论吗
结合我们前面学习的定理的证明方法,你能写出这个性质的证明过程吗?
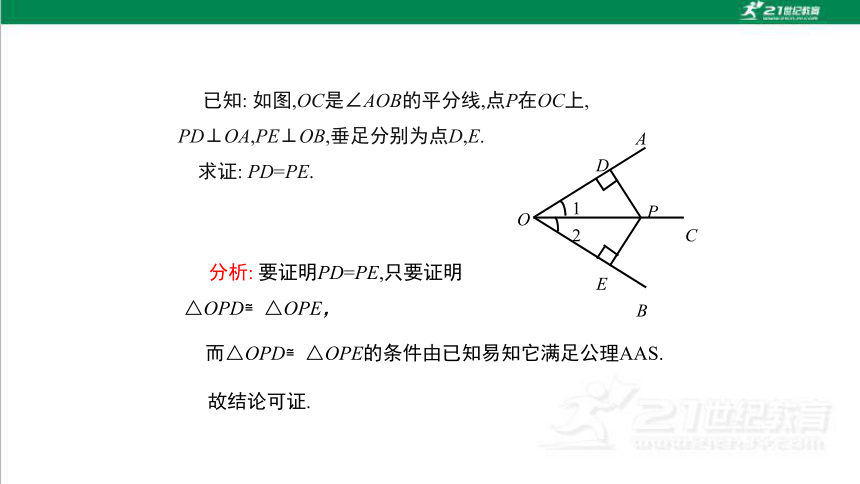
已知: 如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别为点D,E.
求证: PD=PE.
分析: 要证明PD=PE,只要证明△OPD≌△OPE,
而△OPD≌△OPE的条件由已知易知它满足公理AAS.
故结论可证.
C
B
1
A
2
P
D
E
O
证明:
∵ OC是∠AOB的平分线,
∴ ∠1= ∠2.
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO.
∵OP=OP,
∴ △OPD≌△OPE (AAS).
∴ PD=PE.
已知: 如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别为点D,E.
求证: PD=PE.
C
B
1
A
2
P
D
E
O
几何语言表示:
定理:角平分线上的点到这个角的两边的距离相等.
这个结论是经常用来证明两条线段相等的根据之一.
如图,
∵ OC是∠AOB的平分线, 点P是OC上,
PD⊥OA, PE⊥OB, 垂足分别为点D, E (已知),
∴ PD=PE (角平分线上的点到这个角的两边的距离相等).
C
B
1
A
2
P
D
E
O
思考分析
你能写出“定理 角平分线上的点到这个角的两边的距离相等”的逆命题吗
逆命题
在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上.
它是真命题吗
如果是,请你证明它.
已知: 如图, PD=PE, PD⊥OA,
PE⊥OB, 垂足分别为点D,E.
求证: 点P在∠AOB的平分线上.
分析: 要证明点P在∠AOB的平分线上, 可以先作出过点P的射线OC, 然后证明∠POD=∠POE.
B
A
C
D
E
O
P
证明:∵ PD⊥OA ,PE⊥OB,
∴ △POD和△POE都是直角三角形.
∵ PD=PE,OP=OP,
∴ Rt△POD≌Rt△POE(HL).
∴ ∠POD= ∠POE .
∴ OC是∠AOB的平分线.
∴ 点P在∠AOB的平分线上.
已知: 如图, PD=PE, PD⊥OA,
PE⊥OB, 垂足分别为点D,E.
求证: 点P在∠AOB的平分线上.
B
A
C
D
E
O
P
逆定理:在一个角的内部, 并且到角的两边距离相等的点,在这个角的平分线上.
如图,
∵ PD=PE, PD⊥OA, PE⊥OB,
垂足分别为点D, E(已知),
∴点P在∠AOB的平分线上
(在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上).
这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
C
B
1
A
2
P
D
E
O
例1 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为点E,F,且DE=DF,求DE的长.
B
F
E
D
C
A
1. 如图,求作一点P, 使PC=PD, 并且点P到∠AOB的两边的距离相等.
C●
D●
A
B
O
2. 已知: 如图, 在△ABC中, AD是它的角平分线,且BD=CD, DE⊥AB, DF⊥AC, 垂足分别为点E,F.
求证: EB=FC.
B
A
E
D
C
F
证明:
∵ AD是△ABC的角平分线,
且DE⊥AB,DF⊥AC,
∴ DE=DF.
∵BD=CD,
∴Rt△BDE≌Rt△CDF (HL).
∴ EB=FC.
1.角平分线的性质定理
定理:角平分线上的点到这个角的两边的距离相等.
这个结论是经常用来证明两条线段相等的根据之一.
如图,
∵ OC是∠AOB的平分线, P是OC上任意一点,
PD⊥OA, PE⊥OB, 垂足分别为点D, E (已知),
∴ PD=PE (角平分线上的点到这个角的两边的距离相等).
C
B
1
A
2
P
D
E
O
10.5 角平分线
第1课时 角平分线(1)
2.角平分线的判定定理
定理:在一个角的内部, 并且到角的两边距离相等的点,在这个角的平分线上.
如图,∵ PD=PE, PD⊥OA, PE⊥OB,
垂足分别为点D, E(已知),
∴点P在∠AOB的平分线上
(在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上).
这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
C
B
1
A
2
P
D
E
O
习题10.12,第1、3题.
作 业
第十章 三角形的有关证明
10.5 角平分线
第1课时 角平分线(1)
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
这个结论是经常用来证明两条线段相等的根据之一.
A
C
B
P
M
N
如图,
∵ AC=BC, MN⊥AB,
P是MN上任意一点(已知),
∴ PA=PB
(线段垂直平分线上的点到这条线段两个端点的距离相等).
10.5 角平分线
第1课时 角平分线(1)
逆定理: 到线段两个端点距离相等的点在这条线段的垂直平分线上.
几何语言描述:
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上
(到线段两个端点距离相等的点在这条线段的垂直平分线上).
这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
A
B
P
那么结合我们前面学习的有关线段垂直平分线的定理及证明方法,你还记得角平分线上的点有什么性质吗
10.5 角平分线
第1课时 角平分线(1)
1.能够证明角平分线的性质定理及其逆定理;
2.进一步发展自己的推理证明意识和能力,培养将文字语言转化为符号语言、图形语言的能力.
你能利用折纸的方法得到角平分线及角平分线上的点的性质吗
你还记得角平分线上的点有什么性质吗
角平分线上的点到这个角的两边的距离相等.
你能证明这一结论吗
结合我们前面学习的定理的证明方法,你能写出这个性质的证明过程吗?
已知: 如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别为点D,E.
求证: PD=PE.
分析: 要证明PD=PE,只要证明△OPD≌△OPE,
而△OPD≌△OPE的条件由已知易知它满足公理AAS.
故结论可证.
C
B
1
A
2
P
D
E
O
证明:
∵ OC是∠AOB的平分线,
∴ ∠1= ∠2.
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO.
∵OP=OP,
∴ △OPD≌△OPE (AAS).
∴ PD=PE.
已知: 如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别为点D,E.
求证: PD=PE.
C
B
1
A
2
P
D
E
O
几何语言表示:
定理:角平分线上的点到这个角的两边的距离相等.
这个结论是经常用来证明两条线段相等的根据之一.
如图,
∵ OC是∠AOB的平分线, 点P是OC上,
PD⊥OA, PE⊥OB, 垂足分别为点D, E (已知),
∴ PD=PE (角平分线上的点到这个角的两边的距离相等).
C
B
1
A
2
P
D
E
O
思考分析
你能写出“定理 角平分线上的点到这个角的两边的距离相等”的逆命题吗
逆命题
在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上.
它是真命题吗
如果是,请你证明它.
已知: 如图, PD=PE, PD⊥OA,
PE⊥OB, 垂足分别为点D,E.
求证: 点P在∠AOB的平分线上.
分析: 要证明点P在∠AOB的平分线上, 可以先作出过点P的射线OC, 然后证明∠POD=∠POE.
B
A
C
D
E
O
P
证明:∵ PD⊥OA ,PE⊥OB,
∴ △POD和△POE都是直角三角形.
∵ PD=PE,OP=OP,
∴ Rt△POD≌Rt△POE(HL).
∴ ∠POD= ∠POE .
∴ OC是∠AOB的平分线.
∴ 点P在∠AOB的平分线上.
已知: 如图, PD=PE, PD⊥OA,
PE⊥OB, 垂足分别为点D,E.
求证: 点P在∠AOB的平分线上.
B
A
C
D
E
O
P
逆定理:在一个角的内部, 并且到角的两边距离相等的点,在这个角的平分线上.
如图,
∵ PD=PE, PD⊥OA, PE⊥OB,
垂足分别为点D, E(已知),
∴点P在∠AOB的平分线上
(在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上).
这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
C
B
1
A
2
P
D
E
O
例1 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为点E,F,且DE=DF,求DE的长.
B
F
E
D
C
A
1. 如图,求作一点P, 使PC=PD, 并且点P到∠AOB的两边的距离相等.
C●
D●
A
B
O
2. 已知: 如图, 在△ABC中, AD是它的角平分线,且BD=CD, DE⊥AB, DF⊥AC, 垂足分别为点E,F.
求证: EB=FC.
B
A
E
D
C
F
证明:
∵ AD是△ABC的角平分线,
且DE⊥AB,DF⊥AC,
∴ DE=DF.
∵BD=CD,
∴Rt△BDE≌Rt△CDF (HL).
∴ EB=FC.
1.角平分线的性质定理
定理:角平分线上的点到这个角的两边的距离相等.
这个结论是经常用来证明两条线段相等的根据之一.
如图,
∵ OC是∠AOB的平分线, P是OC上任意一点,
PD⊥OA, PE⊥OB, 垂足分别为点D, E (已知),
∴ PD=PE (角平分线上的点到这个角的两边的距离相等).
C
B
1
A
2
P
D
E
O
10.5 角平分线
第1课时 角平分线(1)
2.角平分线的判定定理
定理:在一个角的内部, 并且到角的两边距离相等的点,在这个角的平分线上.
如图,∵ PD=PE, PD⊥OA, PE⊥OB,
垂足分别为点D, E(已知),
∴点P在∠AOB的平分线上
(在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上).
这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
C
B
1
A
2
P
D
E
O
习题10.12,第1、3题.
作 业
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
