2025年高考物理押题预测考前冲刺--相互作用——力(有解析)
文档属性
| 名称 | 2025年高考物理押题预测考前冲刺--相互作用——力(有解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-18 00:00:00 | ||
图片预览



文档简介
2025年高考物理押题预测考前冲刺--相互作用——力
一.选择题(共10小题)
1.(2025 西城区二模)长方体木块A、B叠在一起,放在粗糙水平桌面上。B木块受到一个水平恒力F的作用,两木块始终保持相对静止。下列说法正确的是( )
A.若A、B在桌面上静止不动,A受到向右的摩擦力
B.若A、B一起向右匀速运动,A受到向右的摩擦力
C.若A、B一起向右加速运动,A受到向右的摩擦力
D.若A、B一起向右加速运动,A受到的摩擦力大小等于F
2.(2025 安徽模拟)如图所示,一置于竖直平面内的直杆AB与水平方向的夹角为θ,A、B两端系着一根不可伸长的轻绳,绳长大于直杆AB的长度,轻绳上有一动滑轮,重物悬挂在动滑轮上,系统处于静止状态。现将直杆AB在竖直平面内绕A点顺时针缓慢转过角度2θ。忽略动滑轮与轻绳的摩擦,在此过程中,下列说法正确的是( )
A.轻绳的拉力先增大后减小
B.轻绳的拉力先减小后增大
C.重物受到的合力先减小后增大
D.重物受到的合力先增大后减小
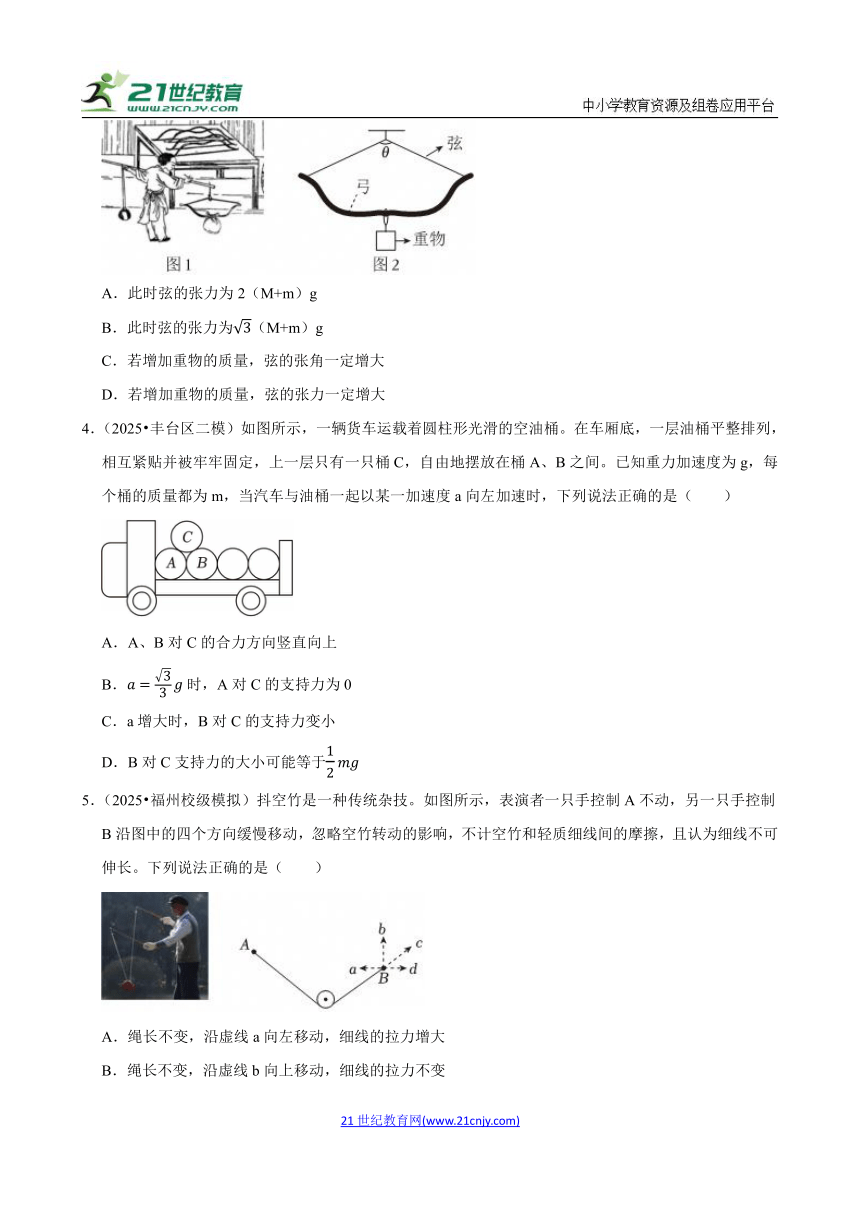
3.(2025 温州三模)宋应星的《天工开物》一书中记录了图1所示的用重物测量弓弦张力的“试弓定力”情景,简化示意图如图2所示,测量时将弦的中点悬挂于秤钩上,在质量为m的弓的中点处悬挂质量为M的重物,稳定时弦的张角θ=120°。弦可视作遵循胡克定律的弹性轻绳,且始终在弹性限度内,不计弓的形变和一切摩擦,重力加速度为g,下列说法正确的是( )
A.此时弦的张力为2(M+m)g
B.此时弦的张力为(M+m)g
C.若增加重物的质量,弦的张角一定增大
D.若增加重物的质量,弦的张力一定增大
4.(2025 丰台区二模)如图所示,一辆货车运载着圆柱形光滑的空油桶。在车厢底,一层油桶平整排列,相互紧贴并被牢牢固定,上一层只有一只桶C,自由地摆放在桶A、B之间。已知重力加速度为g,每个桶的质量都为m,当汽车与油桶一起以某一加速度a向左加速时,下列说法正确的是( )
A.A、B对C的合力方向竖直向上
B.时,A对C的支持力为0
C.a增大时,B对C的支持力变小
D.B对C支持力的大小可能等于
5.(2025 福州校级模拟)抖空竹是一种传统杂技。如图所示,表演者一只手控制A不动,另一只手控制B沿图中的四个方向缓慢移动,忽略空竹转动的影响,不计空竹和轻质细线间的摩擦,且认为细线不可伸长。下列说法正确的是( )
A.绳长不变,沿虚线a向左移动,细线的拉力增大
B.绳长不变,沿虚线b向上移动,细线的拉力不变
C.绳长不变,沿虚线c斜向上移动,细线的拉力不变
D.绳长不变,沿虚线d向右移动,细线对空竹的合力增大
6.(2025 海淀区校级模拟)如图所示,有一个重力不计的方形容器,被水平力F压在竖直的墙面上处于静止状态,现缓慢地向容器内注水,直到将容器刚好盛满为止,在此过程中容器始终保持静止,则下列说法中错误的是( )
A.容器受墙面施加的弹力逐渐变大
B.容器受到的摩擦力逐渐增大
C.水平力F可能不变
D.水平力F可能减小
7.(2025 郑州模拟)如图,一只氢气球通过细绳固定在某处,在水平风力F作用下处于静止状态。设细绳与竖直方向的夹角为α,细绳中拉力为T。因水平风力变化,气球再次平衡时α角变大,则( )
A.风力F变小 B.拉力T不变 C.拉力T变大 D.拉力T变小
8.(2025 成都模拟)用轻质鞋带穿过跑鞋某一鞋孔后系在衣架两端,先后采用图(a)所示衣架水平、图(b)所示衣架倾斜两种方式晾晒在水平粗糙晾衣杆上,两种方式衣架挂钩受到杆的支持力分别为Na与Nb,摩擦力分别为fa与fb,鞋带两端与竖直方向夹角均相等,分别为a与β,鞋带张力分别为Ta与Tb。忽略鞋带与鞋孔间的摩擦,鞋带长度不变。下列说法正确的是( )
A.Na大于Nb B.fa小于fb C.α小于β D.Ta大于Tb
9.(2025 贺兰县校级二模)如图所示,假设卖货郎的每个货筐是质量为M的立方体,每个货筐由四条轻绳对称悬挂于扁担上同一点,则卖货郎肩挑扁担匀速直线前进时,下列说法正确的是( )
A.每条轻绳中的拉力大小为
B.每个货筐上四条轻绳中的拉力相同
C.若将货筐上的四条轻绳减小同样长度但仍对称分布,则每条轻绳中的拉力将变大
D.若将货筐上的四条轻绳减小同样长度但仍对称分布,则轻绳对货筐的作用力将变小
10.(2025 贵阳三模)下列情境中的对象,处于平衡状态的是( )
A.图甲中在轨运行的中国空间站
B.图乙中骑着自行车正在转弯的骑手
C.图丙中站在匀速下行扶梯上的顾客
D.图丁中下落到最低点时的蹦极挑战者
二.多选题(共5小题)
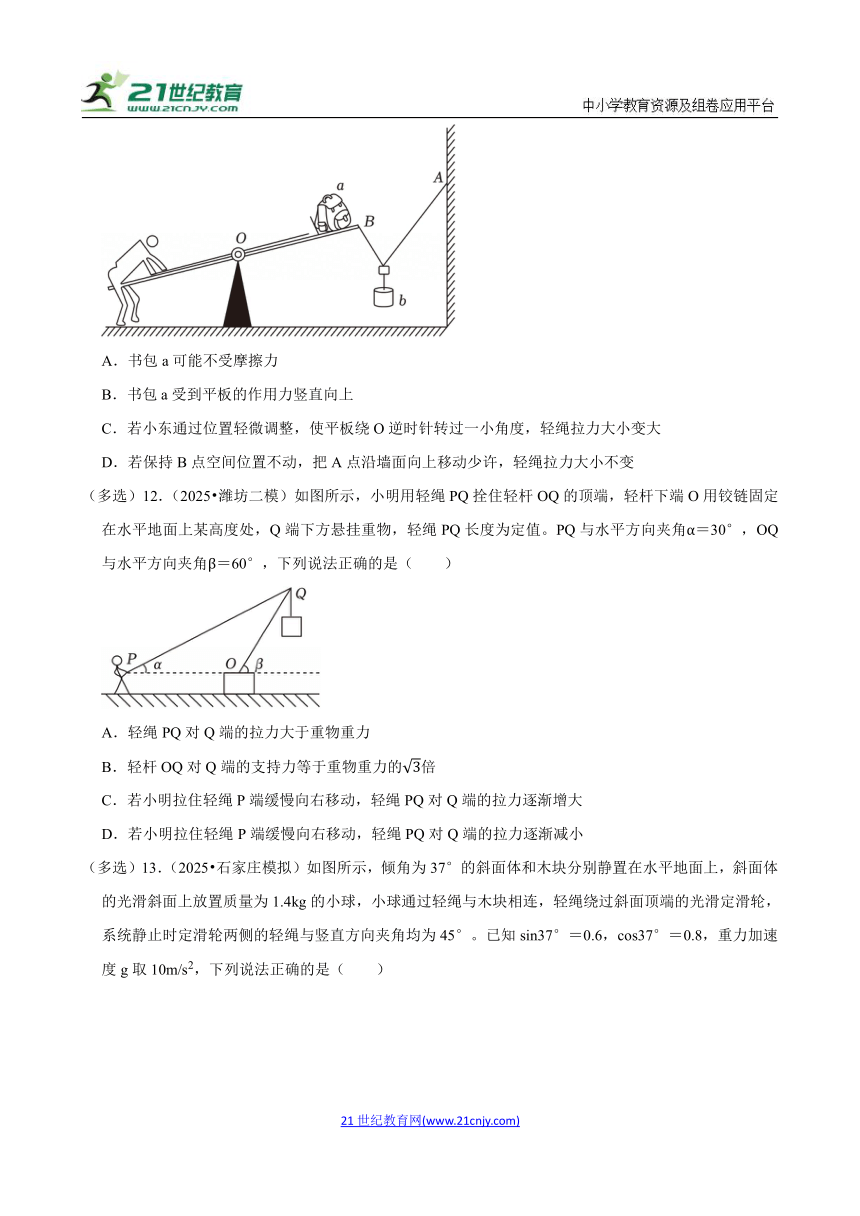
(多选)11.(2025 沈阳模拟)小东放学后将书包a放在跷跷板一侧的平板上,将轻绳一端系在竖直墙面上A点,另一端系在平板右边缘B点,重物b通过挂钩挂在轻绳上,小东坐在跷跷板另一侧,通过位置调整使系统达到平衡,如图所示。不计空气阻力和挂钩与轻绳间摩擦,则( )
A.书包a可能不受摩擦力
B.书包a受到平板的作用力竖直向上
C.若小东通过位置轻微调整,使平板绕O逆时针转过一小角度,轻绳拉力大小变大
D.若保持B点空间位置不动,把A点沿墙面向上移动少许,轻绳拉力大小不变
(多选)12.(2025 潍坊二模)如图所示,小明用轻绳PQ拴住轻杆OQ的顶端,轻杆下端O用铰链固定在水平地面上某高度处,Q端下方悬挂重物,轻绳PQ长度为定值。PQ与水平方向夹角α=30°,OQ与水平方向夹角β=60°,下列说法正确的是( )
A.轻绳PQ对Q端的拉力大于重物重力
B.轻杆OQ对Q端的支持力等于重物重力的倍
C.若小明拉住轻绳P端缓慢向右移动,轻绳PQ对Q端的拉力逐渐增大
D.若小明拉住轻绳P端缓慢向右移动,轻绳PQ对Q端的拉力逐渐减小
(多选)13.(2025 石家庄模拟)如图所示,倾角为37°的斜面体和木块分别静置在水平地面上,斜面体的光滑斜面上放置质量为1.4kg的小球,小球通过轻绳与木块相连,轻绳绕过斜面顶端的光滑定滑轮,系统静止时定滑轮两侧的轻绳与竖直方向夹角均为45°。已知sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,下列说法正确的是( )
A.轻绳对定滑轮的作用力大小等于木块、小球和斜面体的总重力大小
B.地面对木块和斜面体的摩擦力大小相等
C.斜面体对小球的支持力大小10N
D.轻绳对木块的拉力大小为
(多选)14.(2025 丹东模拟)水平地面上叠放了两块石头,均处于静止状态,则下列说法中正确的是( )
A.1石块对2石块的压力是由于1石块发生形变产生的
B.1石块对2石块的压力是由于2石块发生形变产生的
C.若1、2石块间接触面是倾斜的,则2石块与地面之间一定有摩擦力
D.无论1、2石块间接触面是否倾斜,2石块对1石块的作用力一定竖直向上
(多选)15.(2025 山东一模)如图所示,吊车悬臂PM的一端装有大小不计的定滑轮,另一端可绕M点转动,绕过定滑轮的钢索通过四条相同的绳OA、OB、OC、OD吊着一长方形混凝土板。忽略一切摩擦,钢索和绳的质量均不计,当悬臂PM与竖直方向的夹角缓慢减小时,下列说法正确的是( )
A.钢索受到的拉力逐渐变小
B.吊车对地面的摩擦力始终为零
C.钢索对定滑轮的作用力逐渐变大
D.若四条绳增加相同的长度,则四条绳受到的拉力均变大
三.解答题(共5小题)
16.(2025 深圳校级模拟)如图所示,质量均为1kg的物块 A、B静止在水平面上,A、B由劲度系数为3N/cm的轻弹簧相连,物块A套在竖直杆上,在竖直向上的力F作用下沿杆缓慢上移,已知物块 A、B处于水平面时距离为16cm,弹簧原长为18cm,物块B与地面间动摩擦因数μ1为0.75,物块A与杆间动摩擦因数μ2为0.5,设最大静摩擦力等于滑动摩擦力。(g=10m/s2,sin37°=0.6,cos37°=0.8,4.123)
(1)当A在地面时,B所受的摩擦力为多少?
(2)当A上升到c点时,弹簧的弹力恰为使物块B运动的最小值,已知c点的高度hc=0.12m,B运动之前,力F随上升高度h的变化如图所示,求出坐标a、b和Fc的数值。
17.(2024 广东模拟)如图所示,一质量不计的弹簧原长为x0=10cm,一端固定于质量m=2kg的物体上,在另一端施加一水平拉力。若物体与水平面间的动摩擦因数为μ=0.2,最大静摩擦力为fm=4.8N,当弹簧拉长至x=13cm时,物体恰能开始运动(g取10m/s2,弹簧始终在弹性限度内)。
(1)求弹簧的劲度系数k;
(2)当物体做匀速直线运动时,求弹簧长度x1。
18.(2024 辽宁二模)森林着火后,采用直升机运水去灭火,如图所示。直升机下方用绳子吊着水桶,为了方便问题分析,假设直升机与水桶之间用一根不可伸长的轻质绳子相连。直升机运水飞行的过程中,水桶受到的空气阻力与水桶的速度成正比,比例系数为k。若绳子可以承受的最大拉力为F,水桶和水的总质量为m,重力加速度为g。求:
(1)直升机竖直向上加速运动的过程中,水桶的最大加速度;
(2)水桶水平方向做匀速直线运动时,水桶的最大速度及此时绳子与竖直方向的夹角θ。
19.(2024 四川一模)有些家庭或教室的门上安装有一种“暗锁”,在将门关闭的过程中,门锁会自动锁上,这种“暗锁”由外壳A、骨架B、弹簧C、连杆D、锁舌E以及锁槽F等部件组成,如图甲所示.若弹簧的劲度系数为k,锁舌E与外壳A和锁槽F之间的动摩擦因数均为μ,且受到的最大静摩擦力f=μN(N为正压力).当需要在关门时顺便将门锁上,则应在如图乙所示的状态下(此时弹簧的压缩量为x,锁舌E与锁槽F之间的接触点为P),用力拉门,先使锁舌E进入外壳A内,待门关闭后有弹簧将其弹入锁槽F中,从而将门锁上.要顺利完成上述锁门过程,锁舌头部的倾角θ应满足什么条件?
20.(2024 丹东模拟)小明学习了共点力及共点力作用下物体平衡的条件后,对生活中的一些平衡现象产生了浓厚的兴趣,进行了一些研究并获取相关数据,请你协助小明完成以下两个任务:
(1)竖直墙上用一根细绳(轻质)悬挂了一幅相框(如图),经测量:两挂钉之间的细绳长度为70cm,两个挂钉间距离为42cm,相框的重10N,计算出细绳上的张力大小为多少;
(2)长度为2R的筷子AB放入半径为R的半球形空汤碗中恰处于静止状态,测得筷子在碗内的长度为1.6R,计算出这根筷子的重心到A端的距离(筷子与汤碗之间的摩擦不计)。
2025年高考物理押题预测考前冲刺--相互作用——力
参考答案与试题解析
一.选择题(共10小题)
1.(2025 西城区二模)长方体木块A、B叠在一起,放在粗糙水平桌面上。B木块受到一个水平恒力F的作用,两木块始终保持相对静止。下列说法正确的是( )
A.若A、B在桌面上静止不动,A受到向右的摩擦力
B.若A、B一起向右匀速运动,A受到向右的摩擦力
C.若A、B一起向右加速运动,A受到向右的摩擦力
D.若A、B一起向右加速运动,A受到的摩擦力大小等于F
【分析】根据平衡条件和牛顿第二定律进行分析解答。
【解答】解:A.若A、B在桌面上静止不动,根据平衡条件可知,A不受到摩擦力作用,故A错误;
B.若A、B一起向右匀速运动,根据平衡条件可知,A不受到摩擦力作用,故B错误;
C.若A、B一起向右加速运动,根据牛顿第二定律可知,A受到向右的摩擦力,故C正确;
D.若A、B一起向右加速运动,设加速度为a,对A,摩擦力f=mAa,对A、B整体,有F﹣μ(mA+mB)g=(mA+mB)a,可知A受到的摩擦力大小小于F,故D错误。
故选:C。
【点评】考查平衡条件和牛顿第二定律的应用,会根据题意进行准确分析解答。
2.(2025 安徽模拟)如图所示,一置于竖直平面内的直杆AB与水平方向的夹角为θ,A、B两端系着一根不可伸长的轻绳,绳长大于直杆AB的长度,轻绳上有一动滑轮,重物悬挂在动滑轮上,系统处于静止状态。现将直杆AB在竖直平面内绕A点顺时针缓慢转过角度2θ。忽略动滑轮与轻绳的摩擦,在此过程中,下列说法正确的是( )
A.轻绳的拉力先增大后减小
B.轻绳的拉力先减小后增大
C.重物受到的合力先减小后增大
D.重物受到的合力先增大后减小
【分析】根据几何关系,结合平衡条件分析求解。
【解答】解:AB.设直杆AB的长度为l,绳长为L,轻绳与水平方向夹角为α,作如图所示的辅助线
根据几何关系可得:lcosθ=MA,ANcosα+NBcosα=MA,L=AN+NB
联立可得轻绳与水平方向夹角满足:
根据平衡条件可得:2Fsinα=mg
可得轻绳的拉力满足:,直杆从图示位置绕A点顺时针缓慢转过2θ角的过程中,轻绳的拉力先增大再减小,故A正确,B错误;
CD.因为直杆是缓慢运动,所以重物受到的合力一直为0,故C错误,D错误。
故选:A。
【点评】本题考查了基本受力分析,理解动态平衡下物体受力与角度的关系是解决此类问题的关键。
3.(2025 温州三模)宋应星的《天工开物》一书中记录了图1所示的用重物测量弓弦张力的“试弓定力”情景,简化示意图如图2所示,测量时将弦的中点悬挂于秤钩上,在质量为m的弓的中点处悬挂质量为M的重物,稳定时弦的张角θ=120°。弦可视作遵循胡克定律的弹性轻绳,且始终在弹性限度内,不计弓的形变和一切摩擦,重力加速度为g,下列说法正确的是( )
A.此时弦的张力为2(M+m)g
B.此时弦的张力为(M+m)g
C.若增加重物的质量,弦的张角一定增大
D.若增加重物的质量,弦的张力一定增大
【分析】整体法对弓和物体受力分析,竖直方向上由受力平衡列方程进行分析;增加重物质量,弦的伸长量增加,由此分析。
【解答】解:AB、整体法对弓和物体受力分析如图:
竖直方向上由受力平衡可得:2Fcos(M+m)g,
解得:F=(M+m)g,故AB错误;
CD、增加重物质量,弦的伸长量增加,则弦的张力一定增大,弹性轻绳变长,弦的张角一定减小,故C错误、D正确。
故选:D。
【点评】本题主要是考查了共点力的平衡问题,关键是能够确定研究对象、进行受力分析、利用平行四边形法则进行力的合成,然后建立平衡方程进行解答。
4.(2025 丰台区二模)如图所示,一辆货车运载着圆柱形光滑的空油桶。在车厢底,一层油桶平整排列,相互紧贴并被牢牢固定,上一层只有一只桶C,自由地摆放在桶A、B之间。已知重力加速度为g,每个桶的质量都为m,当汽车与油桶一起以某一加速度a向左加速时,下列说法正确的是( )
A.A、B对C的合力方向竖直向上
B.时,A对C的支持力为0
C.a增大时,B对C的支持力变小
D.B对C支持力的大小可能等于
【分析】对C进行受力分析,列牛顿第二定律和平衡方程判断支持力变化;把加速度的数值代入支持力的表达式求支持力。
【解答】解:汽车以某一加速度a向左加速运动时,对C受力分析如图,
竖直方向受力平衡,水平方向根据牛顿第二定律有FBcos30°+FAcos30°=mg,FBsin 30°﹣FAsin 30°=ma,解得,,当加速度a等于时,解得,NA=0,当加速度a大于时,桶A对桶C不再有支持力,则桶C将离开桶A向桶B滚动,a增大时,B对C的支持力变大,B对C支持力的大小不可能等于,A、B对C的合力方向水平向左,故B正确,ACD错误。
故选:B。
【点评】本题主要考查了牛顿第二定律的应用,受力分析,把力分解到两个方向上,列等式是关键,难度不算大。
5.(2025 福州校级模拟)抖空竹是一种传统杂技。如图所示,表演者一只手控制A不动,另一只手控制B沿图中的四个方向缓慢移动,忽略空竹转动的影响,不计空竹和轻质细线间的摩擦,且认为细线不可伸长。下列说法正确的是( )
A.绳长不变,沿虚线a向左移动,细线的拉力增大
B.绳长不变,沿虚线b向上移动,细线的拉力不变
C.绳长不变,沿虚线c斜向上移动,细线的拉力不变
D.绳长不变,沿虚线d向右移动,细线对空竹的合力增大
【分析】以空竹为研究对象,根据平衡条件结合几何关系得到拉力表达式,然后逐项进行分析。
【解答】解:A、空竹受力如图所示,
根据平衡条件可得:2Fsinθ=mg,所以绳拉力:F
设绳长为L,由滑轮和绳子的对称性,有以下几何关系:
沿虚线a向左移动,d减小,θ增大,细线的拉力减小,故A错误;
B、沿虚线b向上移动,d不变,θ不变,细线的拉力不变,故B正确;
C、沿虚线c斜向上移动,d增大,θ减小,细线的拉力增大,故C错误;
D、沿虚线d向右移动,d增大,θ减小,细线的拉力增大,但细线对空竹的合力不变,等于空竹的重力,故D错误。
故选:B。
【点评】本题主要是考查了共点力的平衡问题,关键是能够确定研究对象、进行受力分析、利用平行四边形法则进行力的合成,然后建立平衡方程进行解答。
6.(2025 海淀区校级模拟)如图所示,有一个重力不计的方形容器,被水平力F压在竖直的墙面上处于静止状态,现缓慢地向容器内注水,直到将容器刚好盛满为止,在此过程中容器始终保持静止,则下列说法中错误的是( )
A.容器受墙面施加的弹力逐渐变大
B.容器受到的摩擦力逐渐增大
C.水平力F可能不变
D.水平力F可能减小
【分析】物体始终处于静止状态,受力平衡,合力保持为0;再利用二力平衡的条件再分析其受到的摩擦力和F是否会发生变化。
【解答】解:B、由题知容器始终保持静止状态,受力平衡,所受的摩擦力等于容器和水的总重力,所以容器受到的摩擦力逐渐增大,B正确;
ACD、物体在水平方向上受力平衡,力F可能不变,也可能要增大。故A错误,CD正确。
本题选错误选项,故选:A。
【点评】本题考查了匀变速运动规律的应用,解决本题的关键掌握匀变速直线运动的速度—时间公式、速度—位移公式,并能灵活运用。
7.(2025 郑州模拟)如图,一只氢气球通过细绳固定在某处,在水平风力F作用下处于静止状态。设细绳与竖直方向的夹角为α,细绳中拉力为T。因水平风力变化,气球再次平衡时α角变大,则( )
A.风力F变小 B.拉力T不变 C.拉力T变大 D.拉力T变小
【分析】本题主要考查了物体的平衡条件以及三角函数的应用,通过分析气球在水平和竖直方向上的受力情况,利用平衡条件得出拉力T和风力F与夹角α的关系,进而判断当α变化时T和F的变化情况。
【解答】解:BCD.当角度α变大时,拉力T会变大,对气球进行受力分析,气球受重力G、浮力、绳子拉力T和水平风力F,处于平衡状态。在竖直方向上,Tcosα=F浮﹣G(一般情况下G和F浮不变),当α变大时,cosα变小,为了使等式成立,T必须变大。故BD错误,C正确。
A.对气球进行受力分析,在水平方向上F=Tsinα。由前面分析可知,当α变大时,T也变大,sinα随α增大而增大,所以F=Tsinα会变大。故A错误。
故选:C。
【点评】题目设计较为基础,但能很好地考查学生对受力分析和平衡条件的理解与应用能力,同时也能锻炼学生运用三角函数知识解决物理问题的能力。
8.(2025 成都模拟)用轻质鞋带穿过跑鞋某一鞋孔后系在衣架两端,先后采用图(a)所示衣架水平、图(b)所示衣架倾斜两种方式晾晒在水平粗糙晾衣杆上,两种方式衣架挂钩受到杆的支持力分别为Na与Nb,摩擦力分别为fa与fb,鞋带两端与竖直方向夹角均相等,分别为a与β,鞋带张力分别为Ta与Tb。忽略鞋带与鞋孔间的摩擦,鞋带长度不变。下列说法正确的是( )
A.Na大于Nb B.fa小于fb C.α小于β D.Ta大于Tb
【分析】AB.对跑鞋和衣架整体考虑,根据平衡关系判断;
CD.画出受力情况,根据几何关系分析判断。
【解答】解:AB.对跑鞋和衣架整体考虑,整体受力平衡,如图
则竖直方向上
Na=mg,Nb=mg
所以
Na=Nb
水平方向上没有摩擦力
fa=fb=0
故AB错误;
CD.由于鞋带和鞋孔之间没有摩擦力,则鞋孔两侧的鞋带拉力大小相等,设跑鞋质量为m',则跑鞋水平方向合力为零,所以跑鞋的重力方向沿鞋孔两侧两鞋绳拉力的角平分线,竖直方向
2Tacosα =m'g
2Tbcosβ=m'g
所以
Tacosα=Tbcosβ
鞋带的长度不变,设为L
图(a)所示
图(b)所示
由于
d>d′
则
α>β,Ta>Tb
故C错误,D正确;
故选:D。
【点评】本题考查了基本受力分析,能够熟练地将力进行合成和分解,理解力的平衡条件是解决此类问题的关键。
9.(2025 贺兰县校级二模)如图所示,假设卖货郎的每个货筐是质量为M的立方体,每个货筐由四条轻绳对称悬挂于扁担上同一点,则卖货郎肩挑扁担匀速直线前进时,下列说法正确的是( )
A.每条轻绳中的拉力大小为
B.每个货筐上四条轻绳中的拉力相同
C.若将货筐上的四条轻绳减小同样长度但仍对称分布,则每条轻绳中的拉力将变大
D.若将货筐上的四条轻绳减小同样长度但仍对称分布,则轻绳对货筐的作用力将变小
【分析】卖货郎肩挑扁担匀速直线前进时,货筐受力平衡,根据平衡条件列式求解每条轻绳中的拉力大小;每条轻绳中的拉力大小相等,方向不同;根据拉力表达式,分析拉力的变化情况。
【解答】解:AB、由于四条轻绳对称悬挂于扁担上同一点,则轻绳与竖直方向的夹角相等,绳中拉力大小相等,但方向不同,所以每个货筐上四条轻绳中的拉力不相同。设货筐的质量为M,每条绳与竖直方向的夹角为θ,每条绳中的拉力为F,根据平衡条件可得4Fcosθ=Mg,可得,故AB错误;
CD、若将货筐上的四条轻绳减小同样长度但仍对称分布,则θ变大,cosθ减小,由知,F增大,故C正确,D错误。
故选:C。
【点评】本题是简单的动态平衡问题,要明确研究对象,分析受力情况,根据平衡条件列式分析。
10.(2025 贵阳三模)下列情境中的对象,处于平衡状态的是( )
A.图甲中在轨运行的中国空间站
B.图乙中骑着自行车正在转弯的骑手
C.图丙中站在匀速下行扶梯上的顾客
D.图丁中下落到最低点时的蹦极挑战者
【分析】处于平衡状态的物体,保持静止或匀速直线运动状态。
【解答】解:A、在宇宙中,任何物体都处于失重状态,故A错误;
B、自行车在转弯说明运动状态发生改变,故要受到力的作用,故B错误;
C、站在匀速下行扶梯上的顾客,说明顾客受力平衡,故C正确;
D、下落到最低点时的蹦极挑战者时,挑战者处于超重状态,故D错误。
故选:C。
【点评】此题考查了物体平衡状态的判断,正确理解运动和力的关系是判断的基础。
二.多选题(共5小题)
(多选)11.(2025 沈阳模拟)小东放学后将书包a放在跷跷板一侧的平板上,将轻绳一端系在竖直墙面上A点,另一端系在平板右边缘B点,重物b通过挂钩挂在轻绳上,小东坐在跷跷板另一侧,通过位置调整使系统达到平衡,如图所示。不计空气阻力和挂钩与轻绳间摩擦,则( )
A.书包a可能不受摩擦力
B.书包a受到平板的作用力竖直向上
C.若小东通过位置轻微调整,使平板绕O逆时针转过一小角度,轻绳拉力大小变大
D.若保持B点空间位置不动,把A点沿墙面向上移动少许,轻绳拉力大小不变
【分析】由题可知,书包处于平衡状态,受三个力的作用,分别是自身的重力、垂直板向上的支持力和沿板向上的摩擦力,其中支持力和摩擦力的合力与重力等大反向,即书包受到平板的作用力竖直向上。通过受力分析,跷跷板绕O逆时针转过一个小角度后,d变大,绳子与竖直方向的夹角θ变大,绳上的拉力也变大;如图所示,若保持B点空间位置不动,把A点沿墙面向上移动少许,d不变,绳与竖直方向的夹角θ也不变,故绳上拉力大小不变。
【解答】解:AB.书包处于平衡状态,受三个力的作用,分别是自身的重力、垂直板向上的支持力和沿板向上的摩擦力,其中支持力和摩擦力的合力与重力等大反向,即书包受到平板的作用力竖直向上,故A错误,B正确;
CD.设绳子的总长为L,与竖直方向的夹角为θ,B点与墙的水平距离为d,绳子上的拉力为T,则
2Tcosθ=Gb
解得
如图所示,使跷跷板绕O逆时针转过一个小角度后,d变大,绳子与竖直方向的夹角θ变大,绳上的拉力也变大;若保持B点位置不动,把A点沿墙面向上移动,d不变,则
绳与竖直方向的夹角θ也不变,故绳上拉力大小不变,故CD正确。
故选:BCD。
【点评】本题考查了人在跷跷板上提拉重物的受力分析问题,即共点力平衡问题,画出相应的受力分析图,通过三角函数运算解得。
(多选)12.(2025 潍坊二模)如图所示,小明用轻绳PQ拴住轻杆OQ的顶端,轻杆下端O用铰链固定在水平地面上某高度处,Q端下方悬挂重物,轻绳PQ长度为定值。PQ与水平方向夹角α=30°,OQ与水平方向夹角β=60°,下列说法正确的是( )
A.轻绳PQ对Q端的拉力大于重物重力
B.轻杆OQ对Q端的支持力等于重物重力的倍
C.若小明拉住轻绳P端缓慢向右移动,轻绳PQ对Q端的拉力逐渐增大
D.若小明拉住轻绳P端缓慢向右移动,轻绳PQ对Q端的拉力逐渐减小
【分析】根据平衡条件求解轻绳对O端的拉力和轻杆对O端的支持力;
根据三角形相似分析轻绳PQ对Q端的拉力变化情况。
【解答】解:AB、对节点Q受力分析,如图所示:
′
由几何知识得:绳子PQ与杆OQ的夹角以及重力与杆OQ的夹角均为α=30°
根据平衡条件得:2mgcosα=N,Tsinα=mgsinα
联立解得:T=mg,N,故A错误,B正确;
CD、从O点竖直向上作垂线,交绳与O′点,由重力mg、绳子拉力T和杆的支持力N组成的矢量三角形和三角形△PQO′相似可得:
由几何知识知:OO′变小,绳长lOO′变长,则绳子拉力T变大,故C正确,D错误。
故选:BC。
【点评】本题的难点在于判断P端缓慢向右移动的情况下构造三角形相似分析绳子拉力的 变化。
(多选)13.(2025 石家庄模拟)如图所示,倾角为37°的斜面体和木块分别静置在水平地面上,斜面体的光滑斜面上放置质量为1.4kg的小球,小球通过轻绳与木块相连,轻绳绕过斜面顶端的光滑定滑轮,系统静止时定滑轮两侧的轻绳与竖直方向夹角均为45°。已知sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,下列说法正确的是( )
A.轻绳对定滑轮的作用力大小等于木块、小球和斜面体的总重力大小
B.地面对木块和斜面体的摩擦力大小相等
C.斜面体对小球的支持力大小10N
D.轻绳对木块的拉力大小为
【分析】AD、分别对定滑轮和小球受力分析,沿水平方向和竖直方向建立力平衡的式子,运用平行四边形定则判断轻绳对定滑轮的作用力与木块、小球和斜面体的总重力的关系;
B、分别对木块、小球和斜面整体受力分析,判断地面对二者的摩擦力大小;
C、结合上述分析计算斜面体对小球的支持力;
【解答】解:AD、对各部分进行受力分析,
小球受到重力mg、斜面的支持力N和绳子拉力T。
沿水平方向与竖直方向将小球受到的力分解,得到
水平方向有:Tcos45°=Ncos37°
竖直方向有:Tsin45°+Nsin37°=mg,
代入数据解得:T11.3N。
定滑轮两侧绳子拉力夹角为90°,根据平行四边形定则,轻绳对定滑轮的作用力,而木块、小球和斜面体的总重力远大于此值,故AD错误。
B、对木块受力分析,木块受到绳子拉力T、地面摩擦力f1等,水平方向f1=Tsin45°,
对斜面体和小球整体受力分析,受到绳子拉力T、地面摩擦力f2等,水平方向f2=Tsin45°,
所以地面对木块和斜面体的摩擦力大小相等,故B正确。
C、结合A选项水平方向力的关系Tcos45°=Ncos37°
代入数据解得N≈10N,故C正确。
故选:BC。
【点评】本题考查学生对连接体模型受力平衡问题的分析能力,其中了解轻绳中拉力处处相等,并应用共点力平衡的特点与整体法与隔离法方可解题。
(多选)14.(2025 丹东模拟)水平地面上叠放了两块石头,均处于静止状态,则下列说法中正确的是( )
A.1石块对2石块的压力是由于1石块发生形变产生的
B.1石块对2石块的压力是由于2石块发生形变产生的
C.若1、2石块间接触面是倾斜的,则2石块与地面之间一定有摩擦力
D.无论1、2石块间接触面是否倾斜,2石块对1石块的作用力一定竖直向上
【分析】根据弹力的定义可判断形变和弹力之间的关系,根据共点力平衡知识可判断物体整体受力情况。
【解答】解:AB、1石块发生形变对与它接触的2石块产生弹力,A正确,B错误。
C、若1、2石块间接触面是倾斜的,1石块对2石块向下的压力垂直接触面,必在水平方向上有分力,则2石块与地面之间一定有摩擦力,C正确。
D、无论1、2石块间接触面是否倾斜,1石块所受合力必定为零,则2石块对1石块的作用力必定和重力等大且反向,D正确。
故选:ACD。
【点评】本题考查了弹力的方向,共点力平衡等知识。
(多选)15.(2025 山东一模)如图所示,吊车悬臂PM的一端装有大小不计的定滑轮,另一端可绕M点转动,绕过定滑轮的钢索通过四条相同的绳OA、OB、OC、OD吊着一长方形混凝土板。忽略一切摩擦,钢索和绳的质量均不计,当悬臂PM与竖直方向的夹角缓慢减小时,下列说法正确的是( )
A.钢索受到的拉力逐渐变小
B.吊车对地面的摩擦力始终为零
C.钢索对定滑轮的作用力逐渐变大
D.若四条绳增加相同的长度,则四条绳受到的拉力均变大
【分析】混凝土板受力平衡,根据平衡条件分析钢索对混凝土板的拉力变化情况,由牛顿第三定律判断钢索受到的拉力变化情况。对整体受力分析,根据平衡条件以及牛顿第三定律分析吊车对地面的摩擦力大小;根据力的合成法分析钢索对定滑轮的作用力变化情况。通过平衡条件列式分析四条绳受到的拉力变化情况。
【解答】解:A、当悬臂PM与竖直方向的夹角缓慢减小时,混凝土板受力平衡,由平衡条件得
F=mg
即钢索对混凝土板的拉力保持不变,由牛顿第三定律可知钢索受到的拉力保持不变,故A错误;
B、对整体受力分析,水平方向不受外力,吊车不受地面的摩擦力,由牛顿第三定律可知,吊车对地面的摩擦力始终为零,故B正确;
C、钢索对定滑轮的作用力为两根钢索的合力,悬臂PM与竖直方向的夹角缓慢减小过程中,两根钢索拉力大小不变,夹角变小,所以合力逐渐变大,即钢索对定滑轮的作用力逐渐变大,故C正确;
D、若四条绳增加相同的长度,由几何知识可知绳子与竖直方向夹角θ变小,根据平衡条件有
可知四条绳受到的拉力T均变小,故D错误。
故选:BC。
【点评】本题主要考查共点力平衡问题,解题时需要选准研究对象,做好受力分析,再根据平衡条件确定力与力的关系。
三.解答题(共5小题)
16.(2025 深圳校级模拟)如图所示,质量均为1kg的物块 A、B静止在水平面上,A、B由劲度系数为3N/cm的轻弹簧相连,物块A套在竖直杆上,在竖直向上的力F作用下沿杆缓慢上移,已知物块 A、B处于水平面时距离为16cm,弹簧原长为18cm,物块B与地面间动摩擦因数μ1为0.75,物块A与杆间动摩擦因数μ2为0.5,设最大静摩擦力等于滑动摩擦力。(g=10m/s2,sin37°=0.6,cos37°=0.8,4.123)
(1)当A在地面时,B所受的摩擦力为多少?
(2)当A上升到c点时,弹簧的弹力恰为使物块B运动的最小值,已知c点的高度hc=0.12m,B运动之前,力F随上升高度h的变化如图所示,求出坐标a、b和Fc的数值。
【分析】(1)当A在地面时,由胡克定律求出弹簧的弹力,再由平衡条件求B所受的摩擦力;
(2)以A为研究对象,分析受力情况,由平衡条件、胡克定律、求几何关系坐标a、b、Fc的数值。
【解答】解:已知弹簧劲度系数为k=3N/cm=300N/m;弹簧原长为L0=18cm=0.18m,A、B处于水平面时距离为L1=16cm=0.16m。
(1)当A在地面时,由胡克定律得:弹簧的弹力大小为
F1=k(L0﹣L1)=300×(0.18﹣0.16)=6N
对B,根据平衡条件可得,B所受的摩擦力大小为
f=F1=6N,方向水平向右。
(2)A缓慢向上运动,可以看作是匀速运动过程,同时考虑到F=10N时,向上的力F等于物体A的重力,所以A在a两点受到的弹簧的斜向上的弹力,则:
F﹣mg+Tsinθ﹣μ2 Tcosθ=0
将F=10N以及其他数据代入,得:
cos
此时:tan
所以:ha=L1tanθ=0.16m=0.08m
根据:F﹣mg+Tsinθ﹣μ2 Tcosθ=0
可知,当弹簧的弹力恰好等于0时,即弹簧的长度等于原长时,向上的推力F也可以等于10N,此时:
hbm≈0.0825m
当hc=0.12m时,Lm≈0.20m
此时弹簧的拉力为:
T=k (L﹣L0)=300×(0.20﹣0.18)=6N
对A进行受力分析可知,A受到重力、弹簧的拉力、杆的支持力、向下的摩擦力以及向上的力F的作用:
Fc﹣mg﹣Tsinα﹣μ2 Tcosα=0
tanα,解得:α=37°
联立解得:Fc=16N。
答:(1)当A在地面时,B所受的摩擦力为6N,方向水平向右。
(2)坐标a、b和Fc的数值分别为0.08m、0.0825m、16N。
【点评】该题结合胡克定律考查共点力作用下物体的平衡,解答的关键是使物块B运动的拉力的最小值对应的角度与B的重力无关,解答该最小值对数学三角函数的变换关系要求较高。
17.(2024 广东模拟)如图所示,一质量不计的弹簧原长为x0=10cm,一端固定于质量m=2kg的物体上,在另一端施加一水平拉力。若物体与水平面间的动摩擦因数为μ=0.2,最大静摩擦力为fm=4.8N,当弹簧拉长至x=13cm时,物体恰能开始运动(g取10m/s2,弹簧始终在弹性限度内)。
(1)求弹簧的劲度系数k;
(2)当物体做匀速直线运动时,求弹簧长度x1。
【分析】(1)根据胡克定律F=kx求出劲度系数,其中x为弹簧形变量;
(2)根据胡克定律F=kx求出弹簧的长度。
【解答】解:(1)当弹簧拉长至x=13cm时,物体恰能开始运动,则
k(x﹣x0)=fm
代入数据得:k=160N/m
(2)当物体做匀速直线运动时
k(x1﹣x0)=μmg
解得:x1=12.5cm
答:(1)弹簧的劲度系数k为160N/m;
(2)当物体做匀速直线运动时,弹簧长度x1为12.5cm。
【点评】本题主要考查了胡克定律,解题关键是掌握胡克定律F=kx,其中x为弹簧形变量。
18.(2024 辽宁二模)森林着火后,采用直升机运水去灭火,如图所示。直升机下方用绳子吊着水桶,为了方便问题分析,假设直升机与水桶之间用一根不可伸长的轻质绳子相连。直升机运水飞行的过程中,水桶受到的空气阻力与水桶的速度成正比,比例系数为k。若绳子可以承受的最大拉力为F,水桶和水的总质量为m,重力加速度为g。求:
(1)直升机竖直向上加速运动的过程中,水桶的最大加速度;
(2)水桶水平方向做匀速直线运动时,水桶的最大速度及此时绳子与竖直方向的夹角θ。
【分析】(1)根据空气阻力与速度的关系结合牛顿第二定律列式,分析知道当速度为0,拉力最大时,加速度最大,并求出最大加速度。
(2)水桶水平方向做匀速直线运动时,分析平衡条件以及空气阻力与速度的关系求解。
【解答】解:(1)依题意,水桶受到的空气阻力与水桶的速度成正比,则
f=kv
直升机竖直向上加速运动的过程中,水桶受到重力、拉力和阻力作用,根据牛顿第二定律有
FT﹣mg﹣kv=ma
即
FT=ma+mg+kv
则速度越小,拉力越大,加速度越大,故当速度为0,拉力最大时,加速度最大,解得最大加速度为
(2)水桶水平方向做匀速直线运动时,受力分析,由平衡条件可得
F′sinθ﹣kv=0
F′cosθ=mg
当拉力最大时,速度最大,则
则
答:(1)直升机竖直向上加速运动的过程中,水桶的最大加速度为;
(2)水桶水平方向做匀速直线运动时,水桶的最大速度为,绳子与竖直方向的夹角θ的余弦值为。
【点评】解答本题时,要理清题意,把握空气阻力与速度的关系,根据牛顿第二定律和平衡条件解答。
19.(2024 四川一模)有些家庭或教室的门上安装有一种“暗锁”,在将门关闭的过程中,门锁会自动锁上,这种“暗锁”由外壳A、骨架B、弹簧C、连杆D、锁舌E以及锁槽F等部件组成,如图甲所示.若弹簧的劲度系数为k,锁舌E与外壳A和锁槽F之间的动摩擦因数均为μ,且受到的最大静摩擦力f=μN(N为正压力).当需要在关门时顺便将门锁上,则应在如图乙所示的状态下(此时弹簧的压缩量为x,锁舌E与锁槽F之间的接触点为P),用力拉门,先使锁舌E进入外壳A内,待门关闭后有弹簧将其弹入锁槽F中,从而将门锁上.要顺利完成上述锁门过程,锁舌头部的倾角θ应满足什么条件?
【分析】对锁舌进行受力分析,根据平衡条件分别在互相垂直的方向上列方程,在根据摩擦力计算公式fm=μN,联立方程组求解正压力.无论用多大的力拉门,暗锁仍然能够保持自锁状态,说明正压力N无穷大,根据N的表达式求解θ即可.
【解答】解:设锁舌D受锁槽E的最大静摩擦力为f2,正压力为FN,下表面的正压力为F,弹力为kx,由力的平衡条件可知:
kx+f1+f2cosθ﹣FNsinθ=0…①
F﹣FNcosθ﹣f2sinθ=0…②
f1=μF…③
f2=μFN…④
联立式①②③④,解得正压力的大小:FN
要想完成关门的过程,应满足FN>0,即:(1﹣μ2)sinθ﹣2μcosθ>0
解得:θ
答:锁舌头部的倾角θ应满足条件θ.
【点评】此题关键是对锁舌进行正确的受力分析,解决共点力平衡问题的关键就是对研究对象进行受力分析,不能多力,不能漏力,各个力的方向不能错.
20.(2024 丹东模拟)小明学习了共点力及共点力作用下物体平衡的条件后,对生活中的一些平衡现象产生了浓厚的兴趣,进行了一些研究并获取相关数据,请你协助小明完成以下两个任务:
(1)竖直墙上用一根细绳(轻质)悬挂了一幅相框(如图),经测量:两挂钉之间的细绳长度为70cm,两个挂钉间距离为42cm,相框的重10N,计算出细绳上的张力大小为多少;
(2)长度为2R的筷子AB放入半径为R的半球形空汤碗中恰处于静止状态,测得筷子在碗内的长度为1.6R,计算出这根筷子的重心到A端的距离(筷子与汤碗之间的摩擦不计)。
【分析】(1)以相框为研究对象,分析受力情况,作出力图,由几何关系求出细绳与竖直方向的夹角,再根据平衡条件求解。
(2)对筷子进行受力分析,根据三力汇交原理结合几何知识解答。
【解答】解:(1)设细绳上的张力大小为F,方向与竖直方向成θ角,如图所示。
由几何关系可知
tanθ0.6
则θ=37°
对相框,根据平衡条件有
2Fcos37°=G
解得
F=6.25N
(2)对筷子进行受力分析如图所示。
根据共点力平衡条件,汤碗对筷子在A、C两点的弹力延长线交点一定在过筷子重心的竖直线上,设筷子的重心为N点,则
CN=1.6Rtan2θ=0.9R
则重心到A点的距离为
AN=AC﹣CN=1.6R﹣0.9R=0.7R
即这根筷子的重心到A端的距离为0.7R。
答:(1)细绳上的张力大小为6.25N;
(2)这根筷子的重心到A端的距离为0.7R。
【点评】解答本题的关键要平衡条件的推论:三力汇交原理,并能确定研究对象,加以灵活运用。
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2025 西城区二模)长方体木块A、B叠在一起,放在粗糙水平桌面上。B木块受到一个水平恒力F的作用,两木块始终保持相对静止。下列说法正确的是( )
A.若A、B在桌面上静止不动,A受到向右的摩擦力
B.若A、B一起向右匀速运动,A受到向右的摩擦力
C.若A、B一起向右加速运动,A受到向右的摩擦力
D.若A、B一起向右加速运动,A受到的摩擦力大小等于F
2.(2025 安徽模拟)如图所示,一置于竖直平面内的直杆AB与水平方向的夹角为θ,A、B两端系着一根不可伸长的轻绳,绳长大于直杆AB的长度,轻绳上有一动滑轮,重物悬挂在动滑轮上,系统处于静止状态。现将直杆AB在竖直平面内绕A点顺时针缓慢转过角度2θ。忽略动滑轮与轻绳的摩擦,在此过程中,下列说法正确的是( )
A.轻绳的拉力先增大后减小
B.轻绳的拉力先减小后增大
C.重物受到的合力先减小后增大
D.重物受到的合力先增大后减小
3.(2025 温州三模)宋应星的《天工开物》一书中记录了图1所示的用重物测量弓弦张力的“试弓定力”情景,简化示意图如图2所示,测量时将弦的中点悬挂于秤钩上,在质量为m的弓的中点处悬挂质量为M的重物,稳定时弦的张角θ=120°。弦可视作遵循胡克定律的弹性轻绳,且始终在弹性限度内,不计弓的形变和一切摩擦,重力加速度为g,下列说法正确的是( )
A.此时弦的张力为2(M+m)g
B.此时弦的张力为(M+m)g
C.若增加重物的质量,弦的张角一定增大
D.若增加重物的质量,弦的张力一定增大
4.(2025 丰台区二模)如图所示,一辆货车运载着圆柱形光滑的空油桶。在车厢底,一层油桶平整排列,相互紧贴并被牢牢固定,上一层只有一只桶C,自由地摆放在桶A、B之间。已知重力加速度为g,每个桶的质量都为m,当汽车与油桶一起以某一加速度a向左加速时,下列说法正确的是( )
A.A、B对C的合力方向竖直向上
B.时,A对C的支持力为0
C.a增大时,B对C的支持力变小
D.B对C支持力的大小可能等于
5.(2025 福州校级模拟)抖空竹是一种传统杂技。如图所示,表演者一只手控制A不动,另一只手控制B沿图中的四个方向缓慢移动,忽略空竹转动的影响,不计空竹和轻质细线间的摩擦,且认为细线不可伸长。下列说法正确的是( )
A.绳长不变,沿虚线a向左移动,细线的拉力增大
B.绳长不变,沿虚线b向上移动,细线的拉力不变
C.绳长不变,沿虚线c斜向上移动,细线的拉力不变
D.绳长不变,沿虚线d向右移动,细线对空竹的合力增大
6.(2025 海淀区校级模拟)如图所示,有一个重力不计的方形容器,被水平力F压在竖直的墙面上处于静止状态,现缓慢地向容器内注水,直到将容器刚好盛满为止,在此过程中容器始终保持静止,则下列说法中错误的是( )
A.容器受墙面施加的弹力逐渐变大
B.容器受到的摩擦力逐渐增大
C.水平力F可能不变
D.水平力F可能减小
7.(2025 郑州模拟)如图,一只氢气球通过细绳固定在某处,在水平风力F作用下处于静止状态。设细绳与竖直方向的夹角为α,细绳中拉力为T。因水平风力变化,气球再次平衡时α角变大,则( )
A.风力F变小 B.拉力T不变 C.拉力T变大 D.拉力T变小
8.(2025 成都模拟)用轻质鞋带穿过跑鞋某一鞋孔后系在衣架两端,先后采用图(a)所示衣架水平、图(b)所示衣架倾斜两种方式晾晒在水平粗糙晾衣杆上,两种方式衣架挂钩受到杆的支持力分别为Na与Nb,摩擦力分别为fa与fb,鞋带两端与竖直方向夹角均相等,分别为a与β,鞋带张力分别为Ta与Tb。忽略鞋带与鞋孔间的摩擦,鞋带长度不变。下列说法正确的是( )
A.Na大于Nb B.fa小于fb C.α小于β D.Ta大于Tb
9.(2025 贺兰县校级二模)如图所示,假设卖货郎的每个货筐是质量为M的立方体,每个货筐由四条轻绳对称悬挂于扁担上同一点,则卖货郎肩挑扁担匀速直线前进时,下列说法正确的是( )
A.每条轻绳中的拉力大小为
B.每个货筐上四条轻绳中的拉力相同
C.若将货筐上的四条轻绳减小同样长度但仍对称分布,则每条轻绳中的拉力将变大
D.若将货筐上的四条轻绳减小同样长度但仍对称分布,则轻绳对货筐的作用力将变小
10.(2025 贵阳三模)下列情境中的对象,处于平衡状态的是( )
A.图甲中在轨运行的中国空间站
B.图乙中骑着自行车正在转弯的骑手
C.图丙中站在匀速下行扶梯上的顾客
D.图丁中下落到最低点时的蹦极挑战者
二.多选题(共5小题)
(多选)11.(2025 沈阳模拟)小东放学后将书包a放在跷跷板一侧的平板上,将轻绳一端系在竖直墙面上A点,另一端系在平板右边缘B点,重物b通过挂钩挂在轻绳上,小东坐在跷跷板另一侧,通过位置调整使系统达到平衡,如图所示。不计空气阻力和挂钩与轻绳间摩擦,则( )
A.书包a可能不受摩擦力
B.书包a受到平板的作用力竖直向上
C.若小东通过位置轻微调整,使平板绕O逆时针转过一小角度,轻绳拉力大小变大
D.若保持B点空间位置不动,把A点沿墙面向上移动少许,轻绳拉力大小不变
(多选)12.(2025 潍坊二模)如图所示,小明用轻绳PQ拴住轻杆OQ的顶端,轻杆下端O用铰链固定在水平地面上某高度处,Q端下方悬挂重物,轻绳PQ长度为定值。PQ与水平方向夹角α=30°,OQ与水平方向夹角β=60°,下列说法正确的是( )
A.轻绳PQ对Q端的拉力大于重物重力
B.轻杆OQ对Q端的支持力等于重物重力的倍
C.若小明拉住轻绳P端缓慢向右移动,轻绳PQ对Q端的拉力逐渐增大
D.若小明拉住轻绳P端缓慢向右移动,轻绳PQ对Q端的拉力逐渐减小
(多选)13.(2025 石家庄模拟)如图所示,倾角为37°的斜面体和木块分别静置在水平地面上,斜面体的光滑斜面上放置质量为1.4kg的小球,小球通过轻绳与木块相连,轻绳绕过斜面顶端的光滑定滑轮,系统静止时定滑轮两侧的轻绳与竖直方向夹角均为45°。已知sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,下列说法正确的是( )
A.轻绳对定滑轮的作用力大小等于木块、小球和斜面体的总重力大小
B.地面对木块和斜面体的摩擦力大小相等
C.斜面体对小球的支持力大小10N
D.轻绳对木块的拉力大小为
(多选)14.(2025 丹东模拟)水平地面上叠放了两块石头,均处于静止状态,则下列说法中正确的是( )
A.1石块对2石块的压力是由于1石块发生形变产生的
B.1石块对2石块的压力是由于2石块发生形变产生的
C.若1、2石块间接触面是倾斜的,则2石块与地面之间一定有摩擦力
D.无论1、2石块间接触面是否倾斜,2石块对1石块的作用力一定竖直向上
(多选)15.(2025 山东一模)如图所示,吊车悬臂PM的一端装有大小不计的定滑轮,另一端可绕M点转动,绕过定滑轮的钢索通过四条相同的绳OA、OB、OC、OD吊着一长方形混凝土板。忽略一切摩擦,钢索和绳的质量均不计,当悬臂PM与竖直方向的夹角缓慢减小时,下列说法正确的是( )
A.钢索受到的拉力逐渐变小
B.吊车对地面的摩擦力始终为零
C.钢索对定滑轮的作用力逐渐变大
D.若四条绳增加相同的长度,则四条绳受到的拉力均变大
三.解答题(共5小题)
16.(2025 深圳校级模拟)如图所示,质量均为1kg的物块 A、B静止在水平面上,A、B由劲度系数为3N/cm的轻弹簧相连,物块A套在竖直杆上,在竖直向上的力F作用下沿杆缓慢上移,已知物块 A、B处于水平面时距离为16cm,弹簧原长为18cm,物块B与地面间动摩擦因数μ1为0.75,物块A与杆间动摩擦因数μ2为0.5,设最大静摩擦力等于滑动摩擦力。(g=10m/s2,sin37°=0.6,cos37°=0.8,4.123)
(1)当A在地面时,B所受的摩擦力为多少?
(2)当A上升到c点时,弹簧的弹力恰为使物块B运动的最小值,已知c点的高度hc=0.12m,B运动之前,力F随上升高度h的变化如图所示,求出坐标a、b和Fc的数值。
17.(2024 广东模拟)如图所示,一质量不计的弹簧原长为x0=10cm,一端固定于质量m=2kg的物体上,在另一端施加一水平拉力。若物体与水平面间的动摩擦因数为μ=0.2,最大静摩擦力为fm=4.8N,当弹簧拉长至x=13cm时,物体恰能开始运动(g取10m/s2,弹簧始终在弹性限度内)。
(1)求弹簧的劲度系数k;
(2)当物体做匀速直线运动时,求弹簧长度x1。
18.(2024 辽宁二模)森林着火后,采用直升机运水去灭火,如图所示。直升机下方用绳子吊着水桶,为了方便问题分析,假设直升机与水桶之间用一根不可伸长的轻质绳子相连。直升机运水飞行的过程中,水桶受到的空气阻力与水桶的速度成正比,比例系数为k。若绳子可以承受的最大拉力为F,水桶和水的总质量为m,重力加速度为g。求:
(1)直升机竖直向上加速运动的过程中,水桶的最大加速度;
(2)水桶水平方向做匀速直线运动时,水桶的最大速度及此时绳子与竖直方向的夹角θ。
19.(2024 四川一模)有些家庭或教室的门上安装有一种“暗锁”,在将门关闭的过程中,门锁会自动锁上,这种“暗锁”由外壳A、骨架B、弹簧C、连杆D、锁舌E以及锁槽F等部件组成,如图甲所示.若弹簧的劲度系数为k,锁舌E与外壳A和锁槽F之间的动摩擦因数均为μ,且受到的最大静摩擦力f=μN(N为正压力).当需要在关门时顺便将门锁上,则应在如图乙所示的状态下(此时弹簧的压缩量为x,锁舌E与锁槽F之间的接触点为P),用力拉门,先使锁舌E进入外壳A内,待门关闭后有弹簧将其弹入锁槽F中,从而将门锁上.要顺利完成上述锁门过程,锁舌头部的倾角θ应满足什么条件?
20.(2024 丹东模拟)小明学习了共点力及共点力作用下物体平衡的条件后,对生活中的一些平衡现象产生了浓厚的兴趣,进行了一些研究并获取相关数据,请你协助小明完成以下两个任务:
(1)竖直墙上用一根细绳(轻质)悬挂了一幅相框(如图),经测量:两挂钉之间的细绳长度为70cm,两个挂钉间距离为42cm,相框的重10N,计算出细绳上的张力大小为多少;
(2)长度为2R的筷子AB放入半径为R的半球形空汤碗中恰处于静止状态,测得筷子在碗内的长度为1.6R,计算出这根筷子的重心到A端的距离(筷子与汤碗之间的摩擦不计)。
2025年高考物理押题预测考前冲刺--相互作用——力
参考答案与试题解析
一.选择题(共10小题)
1.(2025 西城区二模)长方体木块A、B叠在一起,放在粗糙水平桌面上。B木块受到一个水平恒力F的作用,两木块始终保持相对静止。下列说法正确的是( )
A.若A、B在桌面上静止不动,A受到向右的摩擦力
B.若A、B一起向右匀速运动,A受到向右的摩擦力
C.若A、B一起向右加速运动,A受到向右的摩擦力
D.若A、B一起向右加速运动,A受到的摩擦力大小等于F
【分析】根据平衡条件和牛顿第二定律进行分析解答。
【解答】解:A.若A、B在桌面上静止不动,根据平衡条件可知,A不受到摩擦力作用,故A错误;
B.若A、B一起向右匀速运动,根据平衡条件可知,A不受到摩擦力作用,故B错误;
C.若A、B一起向右加速运动,根据牛顿第二定律可知,A受到向右的摩擦力,故C正确;
D.若A、B一起向右加速运动,设加速度为a,对A,摩擦力f=mAa,对A、B整体,有F﹣μ(mA+mB)g=(mA+mB)a,可知A受到的摩擦力大小小于F,故D错误。
故选:C。
【点评】考查平衡条件和牛顿第二定律的应用,会根据题意进行准确分析解答。
2.(2025 安徽模拟)如图所示,一置于竖直平面内的直杆AB与水平方向的夹角为θ,A、B两端系着一根不可伸长的轻绳,绳长大于直杆AB的长度,轻绳上有一动滑轮,重物悬挂在动滑轮上,系统处于静止状态。现将直杆AB在竖直平面内绕A点顺时针缓慢转过角度2θ。忽略动滑轮与轻绳的摩擦,在此过程中,下列说法正确的是( )
A.轻绳的拉力先增大后减小
B.轻绳的拉力先减小后增大
C.重物受到的合力先减小后增大
D.重物受到的合力先增大后减小
【分析】根据几何关系,结合平衡条件分析求解。
【解答】解:AB.设直杆AB的长度为l,绳长为L,轻绳与水平方向夹角为α,作如图所示的辅助线
根据几何关系可得:lcosθ=MA,ANcosα+NBcosα=MA,L=AN+NB
联立可得轻绳与水平方向夹角满足:
根据平衡条件可得:2Fsinα=mg
可得轻绳的拉力满足:,直杆从图示位置绕A点顺时针缓慢转过2θ角的过程中,轻绳的拉力先增大再减小,故A正确,B错误;
CD.因为直杆是缓慢运动,所以重物受到的合力一直为0,故C错误,D错误。
故选:A。
【点评】本题考查了基本受力分析,理解动态平衡下物体受力与角度的关系是解决此类问题的关键。
3.(2025 温州三模)宋应星的《天工开物》一书中记录了图1所示的用重物测量弓弦张力的“试弓定力”情景,简化示意图如图2所示,测量时将弦的中点悬挂于秤钩上,在质量为m的弓的中点处悬挂质量为M的重物,稳定时弦的张角θ=120°。弦可视作遵循胡克定律的弹性轻绳,且始终在弹性限度内,不计弓的形变和一切摩擦,重力加速度为g,下列说法正确的是( )
A.此时弦的张力为2(M+m)g
B.此时弦的张力为(M+m)g
C.若增加重物的质量,弦的张角一定增大
D.若增加重物的质量,弦的张力一定增大
【分析】整体法对弓和物体受力分析,竖直方向上由受力平衡列方程进行分析;增加重物质量,弦的伸长量增加,由此分析。
【解答】解:AB、整体法对弓和物体受力分析如图:
竖直方向上由受力平衡可得:2Fcos(M+m)g,
解得:F=(M+m)g,故AB错误;
CD、增加重物质量,弦的伸长量增加,则弦的张力一定增大,弹性轻绳变长,弦的张角一定减小,故C错误、D正确。
故选:D。
【点评】本题主要是考查了共点力的平衡问题,关键是能够确定研究对象、进行受力分析、利用平行四边形法则进行力的合成,然后建立平衡方程进行解答。
4.(2025 丰台区二模)如图所示,一辆货车运载着圆柱形光滑的空油桶。在车厢底,一层油桶平整排列,相互紧贴并被牢牢固定,上一层只有一只桶C,自由地摆放在桶A、B之间。已知重力加速度为g,每个桶的质量都为m,当汽车与油桶一起以某一加速度a向左加速时,下列说法正确的是( )
A.A、B对C的合力方向竖直向上
B.时,A对C的支持力为0
C.a增大时,B对C的支持力变小
D.B对C支持力的大小可能等于
【分析】对C进行受力分析,列牛顿第二定律和平衡方程判断支持力变化;把加速度的数值代入支持力的表达式求支持力。
【解答】解:汽车以某一加速度a向左加速运动时,对C受力分析如图,
竖直方向受力平衡,水平方向根据牛顿第二定律有FBcos30°+FAcos30°=mg,FBsin 30°﹣FAsin 30°=ma,解得,,当加速度a等于时,解得,NA=0,当加速度a大于时,桶A对桶C不再有支持力,则桶C将离开桶A向桶B滚动,a增大时,B对C的支持力变大,B对C支持力的大小不可能等于,A、B对C的合力方向水平向左,故B正确,ACD错误。
故选:B。
【点评】本题主要考查了牛顿第二定律的应用,受力分析,把力分解到两个方向上,列等式是关键,难度不算大。
5.(2025 福州校级模拟)抖空竹是一种传统杂技。如图所示,表演者一只手控制A不动,另一只手控制B沿图中的四个方向缓慢移动,忽略空竹转动的影响,不计空竹和轻质细线间的摩擦,且认为细线不可伸长。下列说法正确的是( )
A.绳长不变,沿虚线a向左移动,细线的拉力增大
B.绳长不变,沿虚线b向上移动,细线的拉力不变
C.绳长不变,沿虚线c斜向上移动,细线的拉力不变
D.绳长不变,沿虚线d向右移动,细线对空竹的合力增大
【分析】以空竹为研究对象,根据平衡条件结合几何关系得到拉力表达式,然后逐项进行分析。
【解答】解:A、空竹受力如图所示,
根据平衡条件可得:2Fsinθ=mg,所以绳拉力:F
设绳长为L,由滑轮和绳子的对称性,有以下几何关系:
沿虚线a向左移动,d减小,θ增大,细线的拉力减小,故A错误;
B、沿虚线b向上移动,d不变,θ不变,细线的拉力不变,故B正确;
C、沿虚线c斜向上移动,d增大,θ减小,细线的拉力增大,故C错误;
D、沿虚线d向右移动,d增大,θ减小,细线的拉力增大,但细线对空竹的合力不变,等于空竹的重力,故D错误。
故选:B。
【点评】本题主要是考查了共点力的平衡问题,关键是能够确定研究对象、进行受力分析、利用平行四边形法则进行力的合成,然后建立平衡方程进行解答。
6.(2025 海淀区校级模拟)如图所示,有一个重力不计的方形容器,被水平力F压在竖直的墙面上处于静止状态,现缓慢地向容器内注水,直到将容器刚好盛满为止,在此过程中容器始终保持静止,则下列说法中错误的是( )
A.容器受墙面施加的弹力逐渐变大
B.容器受到的摩擦力逐渐增大
C.水平力F可能不变
D.水平力F可能减小
【分析】物体始终处于静止状态,受力平衡,合力保持为0;再利用二力平衡的条件再分析其受到的摩擦力和F是否会发生变化。
【解答】解:B、由题知容器始终保持静止状态,受力平衡,所受的摩擦力等于容器和水的总重力,所以容器受到的摩擦力逐渐增大,B正确;
ACD、物体在水平方向上受力平衡,力F可能不变,也可能要增大。故A错误,CD正确。
本题选错误选项,故选:A。
【点评】本题考查了匀变速运动规律的应用,解决本题的关键掌握匀变速直线运动的速度—时间公式、速度—位移公式,并能灵活运用。
7.(2025 郑州模拟)如图,一只氢气球通过细绳固定在某处,在水平风力F作用下处于静止状态。设细绳与竖直方向的夹角为α,细绳中拉力为T。因水平风力变化,气球再次平衡时α角变大,则( )
A.风力F变小 B.拉力T不变 C.拉力T变大 D.拉力T变小
【分析】本题主要考查了物体的平衡条件以及三角函数的应用,通过分析气球在水平和竖直方向上的受力情况,利用平衡条件得出拉力T和风力F与夹角α的关系,进而判断当α变化时T和F的变化情况。
【解答】解:BCD.当角度α变大时,拉力T会变大,对气球进行受力分析,气球受重力G、浮力、绳子拉力T和水平风力F,处于平衡状态。在竖直方向上,Tcosα=F浮﹣G(一般情况下G和F浮不变),当α变大时,cosα变小,为了使等式成立,T必须变大。故BD错误,C正确。
A.对气球进行受力分析,在水平方向上F=Tsinα。由前面分析可知,当α变大时,T也变大,sinα随α增大而增大,所以F=Tsinα会变大。故A错误。
故选:C。
【点评】题目设计较为基础,但能很好地考查学生对受力分析和平衡条件的理解与应用能力,同时也能锻炼学生运用三角函数知识解决物理问题的能力。
8.(2025 成都模拟)用轻质鞋带穿过跑鞋某一鞋孔后系在衣架两端,先后采用图(a)所示衣架水平、图(b)所示衣架倾斜两种方式晾晒在水平粗糙晾衣杆上,两种方式衣架挂钩受到杆的支持力分别为Na与Nb,摩擦力分别为fa与fb,鞋带两端与竖直方向夹角均相等,分别为a与β,鞋带张力分别为Ta与Tb。忽略鞋带与鞋孔间的摩擦,鞋带长度不变。下列说法正确的是( )
A.Na大于Nb B.fa小于fb C.α小于β D.Ta大于Tb
【分析】AB.对跑鞋和衣架整体考虑,根据平衡关系判断;
CD.画出受力情况,根据几何关系分析判断。
【解答】解:AB.对跑鞋和衣架整体考虑,整体受力平衡,如图
则竖直方向上
Na=mg,Nb=mg
所以
Na=Nb
水平方向上没有摩擦力
fa=fb=0
故AB错误;
CD.由于鞋带和鞋孔之间没有摩擦力,则鞋孔两侧的鞋带拉力大小相等,设跑鞋质量为m',则跑鞋水平方向合力为零,所以跑鞋的重力方向沿鞋孔两侧两鞋绳拉力的角平分线,竖直方向
2Tacosα =m'g
2Tbcosβ=m'g
所以
Tacosα=Tbcosβ
鞋带的长度不变,设为L
图(a)所示
图(b)所示
由于
d>d′
则
α>β,Ta>Tb
故C错误,D正确;
故选:D。
【点评】本题考查了基本受力分析,能够熟练地将力进行合成和分解,理解力的平衡条件是解决此类问题的关键。
9.(2025 贺兰县校级二模)如图所示,假设卖货郎的每个货筐是质量为M的立方体,每个货筐由四条轻绳对称悬挂于扁担上同一点,则卖货郎肩挑扁担匀速直线前进时,下列说法正确的是( )
A.每条轻绳中的拉力大小为
B.每个货筐上四条轻绳中的拉力相同
C.若将货筐上的四条轻绳减小同样长度但仍对称分布,则每条轻绳中的拉力将变大
D.若将货筐上的四条轻绳减小同样长度但仍对称分布,则轻绳对货筐的作用力将变小
【分析】卖货郎肩挑扁担匀速直线前进时,货筐受力平衡,根据平衡条件列式求解每条轻绳中的拉力大小;每条轻绳中的拉力大小相等,方向不同;根据拉力表达式,分析拉力的变化情况。
【解答】解:AB、由于四条轻绳对称悬挂于扁担上同一点,则轻绳与竖直方向的夹角相等,绳中拉力大小相等,但方向不同,所以每个货筐上四条轻绳中的拉力不相同。设货筐的质量为M,每条绳与竖直方向的夹角为θ,每条绳中的拉力为F,根据平衡条件可得4Fcosθ=Mg,可得,故AB错误;
CD、若将货筐上的四条轻绳减小同样长度但仍对称分布,则θ变大,cosθ减小,由知,F增大,故C正确,D错误。
故选:C。
【点评】本题是简单的动态平衡问题,要明确研究对象,分析受力情况,根据平衡条件列式分析。
10.(2025 贵阳三模)下列情境中的对象,处于平衡状态的是( )
A.图甲中在轨运行的中国空间站
B.图乙中骑着自行车正在转弯的骑手
C.图丙中站在匀速下行扶梯上的顾客
D.图丁中下落到最低点时的蹦极挑战者
【分析】处于平衡状态的物体,保持静止或匀速直线运动状态。
【解答】解:A、在宇宙中,任何物体都处于失重状态,故A错误;
B、自行车在转弯说明运动状态发生改变,故要受到力的作用,故B错误;
C、站在匀速下行扶梯上的顾客,说明顾客受力平衡,故C正确;
D、下落到最低点时的蹦极挑战者时,挑战者处于超重状态,故D错误。
故选:C。
【点评】此题考查了物体平衡状态的判断,正确理解运动和力的关系是判断的基础。
二.多选题(共5小题)
(多选)11.(2025 沈阳模拟)小东放学后将书包a放在跷跷板一侧的平板上,将轻绳一端系在竖直墙面上A点,另一端系在平板右边缘B点,重物b通过挂钩挂在轻绳上,小东坐在跷跷板另一侧,通过位置调整使系统达到平衡,如图所示。不计空气阻力和挂钩与轻绳间摩擦,则( )
A.书包a可能不受摩擦力
B.书包a受到平板的作用力竖直向上
C.若小东通过位置轻微调整,使平板绕O逆时针转过一小角度,轻绳拉力大小变大
D.若保持B点空间位置不动,把A点沿墙面向上移动少许,轻绳拉力大小不变
【分析】由题可知,书包处于平衡状态,受三个力的作用,分别是自身的重力、垂直板向上的支持力和沿板向上的摩擦力,其中支持力和摩擦力的合力与重力等大反向,即书包受到平板的作用力竖直向上。通过受力分析,跷跷板绕O逆时针转过一个小角度后,d变大,绳子与竖直方向的夹角θ变大,绳上的拉力也变大;如图所示,若保持B点空间位置不动,把A点沿墙面向上移动少许,d不变,绳与竖直方向的夹角θ也不变,故绳上拉力大小不变。
【解答】解:AB.书包处于平衡状态,受三个力的作用,分别是自身的重力、垂直板向上的支持力和沿板向上的摩擦力,其中支持力和摩擦力的合力与重力等大反向,即书包受到平板的作用力竖直向上,故A错误,B正确;
CD.设绳子的总长为L,与竖直方向的夹角为θ,B点与墙的水平距离为d,绳子上的拉力为T,则
2Tcosθ=Gb
解得
如图所示,使跷跷板绕O逆时针转过一个小角度后,d变大,绳子与竖直方向的夹角θ变大,绳上的拉力也变大;若保持B点位置不动,把A点沿墙面向上移动,d不变,则
绳与竖直方向的夹角θ也不变,故绳上拉力大小不变,故CD正确。
故选:BCD。
【点评】本题考查了人在跷跷板上提拉重物的受力分析问题,即共点力平衡问题,画出相应的受力分析图,通过三角函数运算解得。
(多选)12.(2025 潍坊二模)如图所示,小明用轻绳PQ拴住轻杆OQ的顶端,轻杆下端O用铰链固定在水平地面上某高度处,Q端下方悬挂重物,轻绳PQ长度为定值。PQ与水平方向夹角α=30°,OQ与水平方向夹角β=60°,下列说法正确的是( )
A.轻绳PQ对Q端的拉力大于重物重力
B.轻杆OQ对Q端的支持力等于重物重力的倍
C.若小明拉住轻绳P端缓慢向右移动,轻绳PQ对Q端的拉力逐渐增大
D.若小明拉住轻绳P端缓慢向右移动,轻绳PQ对Q端的拉力逐渐减小
【分析】根据平衡条件求解轻绳对O端的拉力和轻杆对O端的支持力;
根据三角形相似分析轻绳PQ对Q端的拉力变化情况。
【解答】解:AB、对节点Q受力分析,如图所示:
′
由几何知识得:绳子PQ与杆OQ的夹角以及重力与杆OQ的夹角均为α=30°
根据平衡条件得:2mgcosα=N,Tsinα=mgsinα
联立解得:T=mg,N,故A错误,B正确;
CD、从O点竖直向上作垂线,交绳与O′点,由重力mg、绳子拉力T和杆的支持力N组成的矢量三角形和三角形△PQO′相似可得:
由几何知识知:OO′变小,绳长lOO′变长,则绳子拉力T变大,故C正确,D错误。
故选:BC。
【点评】本题的难点在于判断P端缓慢向右移动的情况下构造三角形相似分析绳子拉力的 变化。
(多选)13.(2025 石家庄模拟)如图所示,倾角为37°的斜面体和木块分别静置在水平地面上,斜面体的光滑斜面上放置质量为1.4kg的小球,小球通过轻绳与木块相连,轻绳绕过斜面顶端的光滑定滑轮,系统静止时定滑轮两侧的轻绳与竖直方向夹角均为45°。已知sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,下列说法正确的是( )
A.轻绳对定滑轮的作用力大小等于木块、小球和斜面体的总重力大小
B.地面对木块和斜面体的摩擦力大小相等
C.斜面体对小球的支持力大小10N
D.轻绳对木块的拉力大小为
【分析】AD、分别对定滑轮和小球受力分析,沿水平方向和竖直方向建立力平衡的式子,运用平行四边形定则判断轻绳对定滑轮的作用力与木块、小球和斜面体的总重力的关系;
B、分别对木块、小球和斜面整体受力分析,判断地面对二者的摩擦力大小;
C、结合上述分析计算斜面体对小球的支持力;
【解答】解:AD、对各部分进行受力分析,
小球受到重力mg、斜面的支持力N和绳子拉力T。
沿水平方向与竖直方向将小球受到的力分解,得到
水平方向有:Tcos45°=Ncos37°
竖直方向有:Tsin45°+Nsin37°=mg,
代入数据解得:T11.3N。
定滑轮两侧绳子拉力夹角为90°,根据平行四边形定则,轻绳对定滑轮的作用力,而木块、小球和斜面体的总重力远大于此值,故AD错误。
B、对木块受力分析,木块受到绳子拉力T、地面摩擦力f1等,水平方向f1=Tsin45°,
对斜面体和小球整体受力分析,受到绳子拉力T、地面摩擦力f2等,水平方向f2=Tsin45°,
所以地面对木块和斜面体的摩擦力大小相等,故B正确。
C、结合A选项水平方向力的关系Tcos45°=Ncos37°
代入数据解得N≈10N,故C正确。
故选:BC。
【点评】本题考查学生对连接体模型受力平衡问题的分析能力,其中了解轻绳中拉力处处相等,并应用共点力平衡的特点与整体法与隔离法方可解题。
(多选)14.(2025 丹东模拟)水平地面上叠放了两块石头,均处于静止状态,则下列说法中正确的是( )
A.1石块对2石块的压力是由于1石块发生形变产生的
B.1石块对2石块的压力是由于2石块发生形变产生的
C.若1、2石块间接触面是倾斜的,则2石块与地面之间一定有摩擦力
D.无论1、2石块间接触面是否倾斜,2石块对1石块的作用力一定竖直向上
【分析】根据弹力的定义可判断形变和弹力之间的关系,根据共点力平衡知识可判断物体整体受力情况。
【解答】解:AB、1石块发生形变对与它接触的2石块产生弹力,A正确,B错误。
C、若1、2石块间接触面是倾斜的,1石块对2石块向下的压力垂直接触面,必在水平方向上有分力,则2石块与地面之间一定有摩擦力,C正确。
D、无论1、2石块间接触面是否倾斜,1石块所受合力必定为零,则2石块对1石块的作用力必定和重力等大且反向,D正确。
故选:ACD。
【点评】本题考查了弹力的方向,共点力平衡等知识。
(多选)15.(2025 山东一模)如图所示,吊车悬臂PM的一端装有大小不计的定滑轮,另一端可绕M点转动,绕过定滑轮的钢索通过四条相同的绳OA、OB、OC、OD吊着一长方形混凝土板。忽略一切摩擦,钢索和绳的质量均不计,当悬臂PM与竖直方向的夹角缓慢减小时,下列说法正确的是( )
A.钢索受到的拉力逐渐变小
B.吊车对地面的摩擦力始终为零
C.钢索对定滑轮的作用力逐渐变大
D.若四条绳增加相同的长度,则四条绳受到的拉力均变大
【分析】混凝土板受力平衡,根据平衡条件分析钢索对混凝土板的拉力变化情况,由牛顿第三定律判断钢索受到的拉力变化情况。对整体受力分析,根据平衡条件以及牛顿第三定律分析吊车对地面的摩擦力大小;根据力的合成法分析钢索对定滑轮的作用力变化情况。通过平衡条件列式分析四条绳受到的拉力变化情况。
【解答】解:A、当悬臂PM与竖直方向的夹角缓慢减小时,混凝土板受力平衡,由平衡条件得
F=mg
即钢索对混凝土板的拉力保持不变,由牛顿第三定律可知钢索受到的拉力保持不变,故A错误;
B、对整体受力分析,水平方向不受外力,吊车不受地面的摩擦力,由牛顿第三定律可知,吊车对地面的摩擦力始终为零,故B正确;
C、钢索对定滑轮的作用力为两根钢索的合力,悬臂PM与竖直方向的夹角缓慢减小过程中,两根钢索拉力大小不变,夹角变小,所以合力逐渐变大,即钢索对定滑轮的作用力逐渐变大,故C正确;
D、若四条绳增加相同的长度,由几何知识可知绳子与竖直方向夹角θ变小,根据平衡条件有
可知四条绳受到的拉力T均变小,故D错误。
故选:BC。
【点评】本题主要考查共点力平衡问题,解题时需要选准研究对象,做好受力分析,再根据平衡条件确定力与力的关系。
三.解答题(共5小题)
16.(2025 深圳校级模拟)如图所示,质量均为1kg的物块 A、B静止在水平面上,A、B由劲度系数为3N/cm的轻弹簧相连,物块A套在竖直杆上,在竖直向上的力F作用下沿杆缓慢上移,已知物块 A、B处于水平面时距离为16cm,弹簧原长为18cm,物块B与地面间动摩擦因数μ1为0.75,物块A与杆间动摩擦因数μ2为0.5,设最大静摩擦力等于滑动摩擦力。(g=10m/s2,sin37°=0.6,cos37°=0.8,4.123)
(1)当A在地面时,B所受的摩擦力为多少?
(2)当A上升到c点时,弹簧的弹力恰为使物块B运动的最小值,已知c点的高度hc=0.12m,B运动之前,力F随上升高度h的变化如图所示,求出坐标a、b和Fc的数值。
【分析】(1)当A在地面时,由胡克定律求出弹簧的弹力,再由平衡条件求B所受的摩擦力;
(2)以A为研究对象,分析受力情况,由平衡条件、胡克定律、求几何关系坐标a、b、Fc的数值。
【解答】解:已知弹簧劲度系数为k=3N/cm=300N/m;弹簧原长为L0=18cm=0.18m,A、B处于水平面时距离为L1=16cm=0.16m。
(1)当A在地面时,由胡克定律得:弹簧的弹力大小为
F1=k(L0﹣L1)=300×(0.18﹣0.16)=6N
对B,根据平衡条件可得,B所受的摩擦力大小为
f=F1=6N,方向水平向右。
(2)A缓慢向上运动,可以看作是匀速运动过程,同时考虑到F=10N时,向上的力F等于物体A的重力,所以A在a两点受到的弹簧的斜向上的弹力,则:
F﹣mg+Tsinθ﹣μ2 Tcosθ=0
将F=10N以及其他数据代入,得:
cos
此时:tan
所以:ha=L1tanθ=0.16m=0.08m
根据:F﹣mg+Tsinθ﹣μ2 Tcosθ=0
可知,当弹簧的弹力恰好等于0时,即弹簧的长度等于原长时,向上的推力F也可以等于10N,此时:
hbm≈0.0825m
当hc=0.12m时,Lm≈0.20m
此时弹簧的拉力为:
T=k (L﹣L0)=300×(0.20﹣0.18)=6N
对A进行受力分析可知,A受到重力、弹簧的拉力、杆的支持力、向下的摩擦力以及向上的力F的作用:
Fc﹣mg﹣Tsinα﹣μ2 Tcosα=0
tanα,解得:α=37°
联立解得:Fc=16N。
答:(1)当A在地面时,B所受的摩擦力为6N,方向水平向右。
(2)坐标a、b和Fc的数值分别为0.08m、0.0825m、16N。
【点评】该题结合胡克定律考查共点力作用下物体的平衡,解答的关键是使物块B运动的拉力的最小值对应的角度与B的重力无关,解答该最小值对数学三角函数的变换关系要求较高。
17.(2024 广东模拟)如图所示,一质量不计的弹簧原长为x0=10cm,一端固定于质量m=2kg的物体上,在另一端施加一水平拉力。若物体与水平面间的动摩擦因数为μ=0.2,最大静摩擦力为fm=4.8N,当弹簧拉长至x=13cm时,物体恰能开始运动(g取10m/s2,弹簧始终在弹性限度内)。
(1)求弹簧的劲度系数k;
(2)当物体做匀速直线运动时,求弹簧长度x1。
【分析】(1)根据胡克定律F=kx求出劲度系数,其中x为弹簧形变量;
(2)根据胡克定律F=kx求出弹簧的长度。
【解答】解:(1)当弹簧拉长至x=13cm时,物体恰能开始运动,则
k(x﹣x0)=fm
代入数据得:k=160N/m
(2)当物体做匀速直线运动时
k(x1﹣x0)=μmg
解得:x1=12.5cm
答:(1)弹簧的劲度系数k为160N/m;
(2)当物体做匀速直线运动时,弹簧长度x1为12.5cm。
【点评】本题主要考查了胡克定律,解题关键是掌握胡克定律F=kx,其中x为弹簧形变量。
18.(2024 辽宁二模)森林着火后,采用直升机运水去灭火,如图所示。直升机下方用绳子吊着水桶,为了方便问题分析,假设直升机与水桶之间用一根不可伸长的轻质绳子相连。直升机运水飞行的过程中,水桶受到的空气阻力与水桶的速度成正比,比例系数为k。若绳子可以承受的最大拉力为F,水桶和水的总质量为m,重力加速度为g。求:
(1)直升机竖直向上加速运动的过程中,水桶的最大加速度;
(2)水桶水平方向做匀速直线运动时,水桶的最大速度及此时绳子与竖直方向的夹角θ。
【分析】(1)根据空气阻力与速度的关系结合牛顿第二定律列式,分析知道当速度为0,拉力最大时,加速度最大,并求出最大加速度。
(2)水桶水平方向做匀速直线运动时,分析平衡条件以及空气阻力与速度的关系求解。
【解答】解:(1)依题意,水桶受到的空气阻力与水桶的速度成正比,则
f=kv
直升机竖直向上加速运动的过程中,水桶受到重力、拉力和阻力作用,根据牛顿第二定律有
FT﹣mg﹣kv=ma
即
FT=ma+mg+kv
则速度越小,拉力越大,加速度越大,故当速度为0,拉力最大时,加速度最大,解得最大加速度为
(2)水桶水平方向做匀速直线运动时,受力分析,由平衡条件可得
F′sinθ﹣kv=0
F′cosθ=mg
当拉力最大时,速度最大,则
则
答:(1)直升机竖直向上加速运动的过程中,水桶的最大加速度为;
(2)水桶水平方向做匀速直线运动时,水桶的最大速度为,绳子与竖直方向的夹角θ的余弦值为。
【点评】解答本题时,要理清题意,把握空气阻力与速度的关系,根据牛顿第二定律和平衡条件解答。
19.(2024 四川一模)有些家庭或教室的门上安装有一种“暗锁”,在将门关闭的过程中,门锁会自动锁上,这种“暗锁”由外壳A、骨架B、弹簧C、连杆D、锁舌E以及锁槽F等部件组成,如图甲所示.若弹簧的劲度系数为k,锁舌E与外壳A和锁槽F之间的动摩擦因数均为μ,且受到的最大静摩擦力f=μN(N为正压力).当需要在关门时顺便将门锁上,则应在如图乙所示的状态下(此时弹簧的压缩量为x,锁舌E与锁槽F之间的接触点为P),用力拉门,先使锁舌E进入外壳A内,待门关闭后有弹簧将其弹入锁槽F中,从而将门锁上.要顺利完成上述锁门过程,锁舌头部的倾角θ应满足什么条件?
【分析】对锁舌进行受力分析,根据平衡条件分别在互相垂直的方向上列方程,在根据摩擦力计算公式fm=μN,联立方程组求解正压力.无论用多大的力拉门,暗锁仍然能够保持自锁状态,说明正压力N无穷大,根据N的表达式求解θ即可.
【解答】解:设锁舌D受锁槽E的最大静摩擦力为f2,正压力为FN,下表面的正压力为F,弹力为kx,由力的平衡条件可知:
kx+f1+f2cosθ﹣FNsinθ=0…①
F﹣FNcosθ﹣f2sinθ=0…②
f1=μF…③
f2=μFN…④
联立式①②③④,解得正压力的大小:FN
要想完成关门的过程,应满足FN>0,即:(1﹣μ2)sinθ﹣2μcosθ>0
解得:θ
答:锁舌头部的倾角θ应满足条件θ.
【点评】此题关键是对锁舌进行正确的受力分析,解决共点力平衡问题的关键就是对研究对象进行受力分析,不能多力,不能漏力,各个力的方向不能错.
20.(2024 丹东模拟)小明学习了共点力及共点力作用下物体平衡的条件后,对生活中的一些平衡现象产生了浓厚的兴趣,进行了一些研究并获取相关数据,请你协助小明完成以下两个任务:
(1)竖直墙上用一根细绳(轻质)悬挂了一幅相框(如图),经测量:两挂钉之间的细绳长度为70cm,两个挂钉间距离为42cm,相框的重10N,计算出细绳上的张力大小为多少;
(2)长度为2R的筷子AB放入半径为R的半球形空汤碗中恰处于静止状态,测得筷子在碗内的长度为1.6R,计算出这根筷子的重心到A端的距离(筷子与汤碗之间的摩擦不计)。
【分析】(1)以相框为研究对象,分析受力情况,作出力图,由几何关系求出细绳与竖直方向的夹角,再根据平衡条件求解。
(2)对筷子进行受力分析,根据三力汇交原理结合几何知识解答。
【解答】解:(1)设细绳上的张力大小为F,方向与竖直方向成θ角,如图所示。
由几何关系可知
tanθ0.6
则θ=37°
对相框,根据平衡条件有
2Fcos37°=G
解得
F=6.25N
(2)对筷子进行受力分析如图所示。
根据共点力平衡条件,汤碗对筷子在A、C两点的弹力延长线交点一定在过筷子重心的竖直线上,设筷子的重心为N点,则
CN=1.6Rtan2θ=0.9R
则重心到A点的距离为
AN=AC﹣CN=1.6R﹣0.9R=0.7R
即这根筷子的重心到A端的距离为0.7R。
答:(1)细绳上的张力大小为6.25N;
(2)这根筷子的重心到A端的距离为0.7R。
【点评】解答本题的关键要平衡条件的推论:三力汇交原理,并能确定研究对象,加以灵活运用。
21世纪教育网(www.21cnjy.com)
同课章节目录
