第二十一章一元二次方程 单元检测卷(含答案)人教版数学九年级上册
文档属性
| 名称 | 第二十一章一元二次方程 单元检测卷(含答案)人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 42.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-18 20:00:30 | ||
图片预览



文档简介
人教版数学九年级上册
《一元二次方程》单元检测卷
一 、选择题
1.下列方程中是关于x的一元二次方程的是( )
A.x2+=0 B.ax2+bx+c=0
C.(x﹣1)(x+2)=1 D.3x2﹣2xy﹣5y2=0
2.一元二次方程4x2﹣3x﹣5=0的一次项系数是( )
A.﹣5 B.4 C.﹣3 D.3
3.如果x=4是一元二次方程x2﹣3x=a2的一个根,那么常数a的值是( )
A.2 B.﹣2 C.±2 D.±4
4.根据下表判断方程x2+x﹣3=0的一个根的近似值(精确到0.1)是( )
x 1.2 1.3 1.4 1.5
x2+x﹣3 ﹣0.36 ﹣0.01 0.36 0.75
A.1.3 B.1.2 C.1.5 D.1.4
5.方程(x﹣3)2=0的根是( )
A.x=3 B.x=0 C.x1=x2=3 D.x1=3,x2=﹣3
6.用配方法解方程x2﹣6x﹣8=0时,配方正确的是( )
A.(x﹣3)2=17 B.(x﹣3)2=14
C.(x﹣6)2=44 D.(x﹣3)2=1
7.用公式法解方程5x2﹣6=7x,下列代入公式正确的是( )
A.x=
B.x=
C.x=
D.x=
8.方程2x(x﹣3)=5(x﹣3)的根为( )
A.x=2.5 B.x=3 C.x=2.5或x=3 D.非上述答案
9.一元二次方程x2+ax+a﹣1=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.有实数根 D.没有实数根
10.已知x1,x2是方程2x2+x-2=0的两个实数根,则x+x的值是( )
A.- B.1 C. D.9
11.某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,第一季度共获利42万元,已知二月份和三月份利润的月增长率相同.设二.三月份利润的月增长率x,那么x满足的方程为( )
A.10(1+x)2=42
B.10+10(1+x)2=42
C.10+10(1+x)+10(1+2x)=42
D.10+10(1+x)+10(1+x)2=42
12.商场将进价为2 000元/台的冰箱以2 400元/台售出,平均每天能售出8台.为了促销,商场决定采取适当的降价措施,调查表明:这种冰箱的售价每台每降低50元,平均每天就能多售出4台,商场要想在这种冰箱销售中每天盈利4 800元,同时又要使消费者得到更多实惠,每台冰箱应降价( )
A.100元 B.200元 C.300元 D.400元
二 、填空题
13.把一元二次方程(x+1)(1﹣x)=2x化成二次项系数大于零的一般式为 ,其中二次项系数是 ,一次项系数是 ,常数项是 .
14.三角形一边长为10,另两边长是方程x2﹣14x+48=0的两实根,则这是一个______三角形,面积为________.
15.关于x的一元二次方程(a﹣5)x2﹣4x﹣1=0有实数根,则实数a的取值范围是 .
16.若方程x2﹣4x+1=0的两根是x1,x2,则x1(1+x2)+x2的值为 .
17.中国民歌不仅脍炙人口,而且许多还有教育意义,有一首《牧童王小良》的民歌还包含着一个数学问题:牧童王小良,放牧一群羊.问他羊几只,请你仔细想.头数加只数,只数减头数.只数乘头数,只数除头数.四数连加起,正好一百数.如果设羊的只数为x,那么根据民歌的大意,你能列出的方程是 .
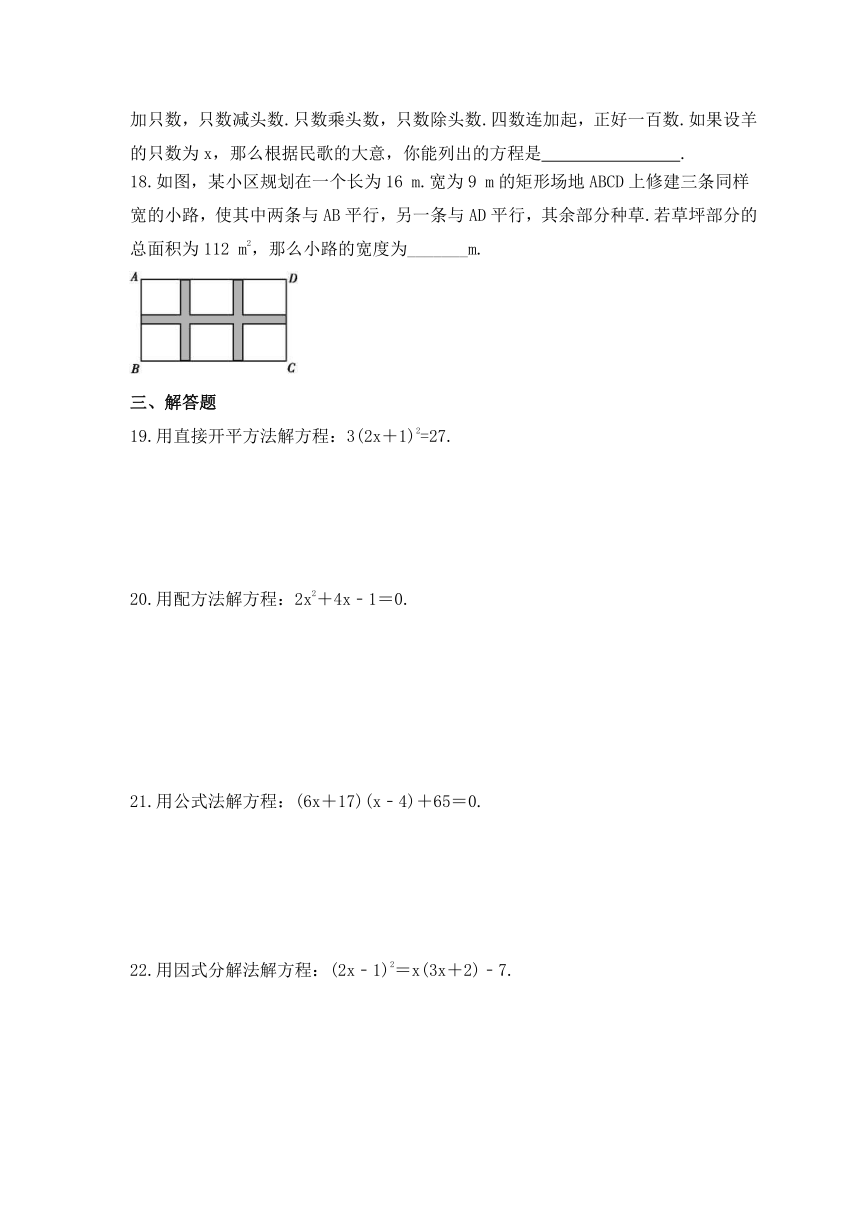
18.如图,某小区规划在一个长为16 m.宽为9 m的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若草坪部分的总面积为112 m2,那么小路的宽度为_______m.
三 、解答题
19.用直接开平方法解方程:3(2x+1)2=27.
20.用配方法解方程:2x2+4x﹣1=0.
21.用公式法解方程:(6x+17)(x﹣4)+65=0.
22.用因式分解法解方程:(2x﹣1)2=x(3x+2)﹣7.
23.已知关于x的一元二次方程(a﹣c)x2﹣2bx+(a+c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
24.已知关于x的一元二次方程2x2﹣mx﹣2m+1=0的两根的平方和是,求m的值.
25.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分枝,主干,支干和小分枝的总数是73,每个支干长出多少分枝?
26.如图,在△ABC中,AB=10 cm,BC=16 cm,∠B=90°,点P从点A开始沿着AB边向点B以1 cm/s的速度移动(到B停止),点Q从点B开始沿着BC边向点C以2 cm/s的速度移动(到C停止).如果P.Q分别从A.B同时出发,经过几秒,△PBQ的面积是△ABC面积的
27.元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果的利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲.乙两种苹果的进价分别是每千克多少元;
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价均提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
答案
1.C.
2.C
3.C.
4.A
5.C
6.A
7.B
8.C.
9.C
10.C.
11.D.
12.B
13.答案为:x2+2x﹣1=0,1,2,﹣1
14.答案为:直角;24.
15.答案为a≥1且a≠5.
16.答案为:5.
17.答案为:x2+2x+1=100.
18.答案为:1.
19.解:(2x+1)2=9
2x+1=±3.
2x+1=3或2x+1=-3
x1=1或x2=-2.
20.解:x2+2x﹣=0,x2+2x=,
x2+2x+12=+12,
∴(x+1)2=,∴x+1=±,
∴x1=,x2=.
21.解:原方程可化为6x2﹣7x﹣3=0.
∵a=6,b=﹣7,c=﹣3,∴b2﹣4ac=121,
∴y==,
∴x1=,x2=﹣.
22.解:(2x﹣1)2=x(3x+2)﹣7,
4x2﹣4x+1=3x2+2x﹣7,
x2﹣6x+8=0,
x1=2,x2=4.
23.解:(1)∵x=1是一元二次方程(a﹣c)x2﹣2bx+(a+c)=0的根,
∴(a﹣c)﹣2b+(a+c)=0,∴a=b,
∵a﹣c≠0,
∴a≠c,∴△ABC为等腰三角形;
(2)∵方程有两个相等的实数根,
∴b2﹣4ac=0,即4b2﹣4(a+c)(a﹣c)=0,
∴b2+c2=a2,
∴△ABC为直角三角形.
24.解:设方程两根为x1,x2,由已知得
∵x12+x22=(x1+x2)2﹣2x1x2=,即(m)2﹣2×=,
∴m2+8m﹣33=0.解得m1=﹣11,m2=3.
当m=﹣11时,方程为2x2+11x+23=0,Δ=112﹣4×2×23<0,方程无实数根,
∴m=﹣11不合题意,舍去;
当m=3时,方程为2x2﹣3x﹣5=0,Δ=(﹣3)2﹣4×2×(﹣5)>0,
方程有两个不相等的实数根,符合题意.
∴m的值为3.
25.解:由题意得1+x+x x=73,
即x2+x﹣72=0,
∴(x+9)(x﹣8)=0,解得x1=8,x2=﹣9(舍去)
答:每个支干长出8个小分支.
26.解:设经过x秒,△PBQ的面积是△ABC面积的.
当0整理得x2﹣10x+24=0,解得x1=4,x2=6.
当8整理得16x=112,解得x=7(不合题意,舍去).
答:经过4秒或6秒,△PBQ的面积是△ABC面积的.
27.解:(1)设甲种苹果的进价为a元/千克,乙种苹果的进价为b元/千克,
根据题意得解得
答:甲种苹果的进价为10元/千克,乙种苹果的进价为8元/千克.
(2)根据题意得(4+x)(100﹣10x)+(2+x)(140﹣10x)=960,
整理得x2﹣9x+14=0,
解得x1=2,x2=7,经检验,x1=2,x2=7均符合题意.
答:x的值为2或7.
《一元二次方程》单元检测卷
一 、选择题
1.下列方程中是关于x的一元二次方程的是( )
A.x2+=0 B.ax2+bx+c=0
C.(x﹣1)(x+2)=1 D.3x2﹣2xy﹣5y2=0
2.一元二次方程4x2﹣3x﹣5=0的一次项系数是( )
A.﹣5 B.4 C.﹣3 D.3
3.如果x=4是一元二次方程x2﹣3x=a2的一个根,那么常数a的值是( )
A.2 B.﹣2 C.±2 D.±4
4.根据下表判断方程x2+x﹣3=0的一个根的近似值(精确到0.1)是( )
x 1.2 1.3 1.4 1.5
x2+x﹣3 ﹣0.36 ﹣0.01 0.36 0.75
A.1.3 B.1.2 C.1.5 D.1.4
5.方程(x﹣3)2=0的根是( )
A.x=3 B.x=0 C.x1=x2=3 D.x1=3,x2=﹣3
6.用配方法解方程x2﹣6x﹣8=0时,配方正确的是( )
A.(x﹣3)2=17 B.(x﹣3)2=14
C.(x﹣6)2=44 D.(x﹣3)2=1
7.用公式法解方程5x2﹣6=7x,下列代入公式正确的是( )
A.x=
B.x=
C.x=
D.x=
8.方程2x(x﹣3)=5(x﹣3)的根为( )
A.x=2.5 B.x=3 C.x=2.5或x=3 D.非上述答案
9.一元二次方程x2+ax+a﹣1=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.有实数根 D.没有实数根
10.已知x1,x2是方程2x2+x-2=0的两个实数根,则x+x的值是( )
A.- B.1 C. D.9
11.某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,第一季度共获利42万元,已知二月份和三月份利润的月增长率相同.设二.三月份利润的月增长率x,那么x满足的方程为( )
A.10(1+x)2=42
B.10+10(1+x)2=42
C.10+10(1+x)+10(1+2x)=42
D.10+10(1+x)+10(1+x)2=42
12.商场将进价为2 000元/台的冰箱以2 400元/台售出,平均每天能售出8台.为了促销,商场决定采取适当的降价措施,调查表明:这种冰箱的售价每台每降低50元,平均每天就能多售出4台,商场要想在这种冰箱销售中每天盈利4 800元,同时又要使消费者得到更多实惠,每台冰箱应降价( )
A.100元 B.200元 C.300元 D.400元
二 、填空题
13.把一元二次方程(x+1)(1﹣x)=2x化成二次项系数大于零的一般式为 ,其中二次项系数是 ,一次项系数是 ,常数项是 .
14.三角形一边长为10,另两边长是方程x2﹣14x+48=0的两实根,则这是一个______三角形,面积为________.
15.关于x的一元二次方程(a﹣5)x2﹣4x﹣1=0有实数根,则实数a的取值范围是 .
16.若方程x2﹣4x+1=0的两根是x1,x2,则x1(1+x2)+x2的值为 .
17.中国民歌不仅脍炙人口,而且许多还有教育意义,有一首《牧童王小良》的民歌还包含着一个数学问题:牧童王小良,放牧一群羊.问他羊几只,请你仔细想.头数加只数,只数减头数.只数乘头数,只数除头数.四数连加起,正好一百数.如果设羊的只数为x,那么根据民歌的大意,你能列出的方程是 .
18.如图,某小区规划在一个长为16 m.宽为9 m的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若草坪部分的总面积为112 m2,那么小路的宽度为_______m.
三 、解答题
19.用直接开平方法解方程:3(2x+1)2=27.
20.用配方法解方程:2x2+4x﹣1=0.
21.用公式法解方程:(6x+17)(x﹣4)+65=0.
22.用因式分解法解方程:(2x﹣1)2=x(3x+2)﹣7.
23.已知关于x的一元二次方程(a﹣c)x2﹣2bx+(a+c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
24.已知关于x的一元二次方程2x2﹣mx﹣2m+1=0的两根的平方和是,求m的值.
25.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分枝,主干,支干和小分枝的总数是73,每个支干长出多少分枝?
26.如图,在△ABC中,AB=10 cm,BC=16 cm,∠B=90°,点P从点A开始沿着AB边向点B以1 cm/s的速度移动(到B停止),点Q从点B开始沿着BC边向点C以2 cm/s的速度移动(到C停止).如果P.Q分别从A.B同时出发,经过几秒,△PBQ的面积是△ABC面积的
27.元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果的利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲.乙两种苹果的进价分别是每千克多少元;
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价均提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
答案
1.C.
2.C
3.C.
4.A
5.C
6.A
7.B
8.C.
9.C
10.C.
11.D.
12.B
13.答案为:x2+2x﹣1=0,1,2,﹣1
14.答案为:直角;24.
15.答案为a≥1且a≠5.
16.答案为:5.
17.答案为:x2+2x+1=100.
18.答案为:1.
19.解:(2x+1)2=9
2x+1=±3.
2x+1=3或2x+1=-3
x1=1或x2=-2.
20.解:x2+2x﹣=0,x2+2x=,
x2+2x+12=+12,
∴(x+1)2=,∴x+1=±,
∴x1=,x2=.
21.解:原方程可化为6x2﹣7x﹣3=0.
∵a=6,b=﹣7,c=﹣3,∴b2﹣4ac=121,
∴y==,
∴x1=,x2=﹣.
22.解:(2x﹣1)2=x(3x+2)﹣7,
4x2﹣4x+1=3x2+2x﹣7,
x2﹣6x+8=0,
x1=2,x2=4.
23.解:(1)∵x=1是一元二次方程(a﹣c)x2﹣2bx+(a+c)=0的根,
∴(a﹣c)﹣2b+(a+c)=0,∴a=b,
∵a﹣c≠0,
∴a≠c,∴△ABC为等腰三角形;
(2)∵方程有两个相等的实数根,
∴b2﹣4ac=0,即4b2﹣4(a+c)(a﹣c)=0,
∴b2+c2=a2,
∴△ABC为直角三角形.
24.解:设方程两根为x1,x2,由已知得
∵x12+x22=(x1+x2)2﹣2x1x2=,即(m)2﹣2×=,
∴m2+8m﹣33=0.解得m1=﹣11,m2=3.
当m=﹣11时,方程为2x2+11x+23=0,Δ=112﹣4×2×23<0,方程无实数根,
∴m=﹣11不合题意,舍去;
当m=3时,方程为2x2﹣3x﹣5=0,Δ=(﹣3)2﹣4×2×(﹣5)>0,
方程有两个不相等的实数根,符合题意.
∴m的值为3.
25.解:由题意得1+x+x x=73,
即x2+x﹣72=0,
∴(x+9)(x﹣8)=0,解得x1=8,x2=﹣9(舍去)
答:每个支干长出8个小分支.
26.解:设经过x秒,△PBQ的面积是△ABC面积的.
当0
当8
答:经过4秒或6秒,△PBQ的面积是△ABC面积的.
27.解:(1)设甲种苹果的进价为a元/千克,乙种苹果的进价为b元/千克,
根据题意得解得
答:甲种苹果的进价为10元/千克,乙种苹果的进价为8元/千克.
(2)根据题意得(4+x)(100﹣10x)+(2+x)(140﹣10x)=960,
整理得x2﹣9x+14=0,
解得x1=2,x2=7,经检验,x1=2,x2=7均符合题意.
答:x的值为2或7.
同课章节目录
