第二十六章 解直角三角形 单元测试(含详解) 冀教版数学九年级上册
文档属性
| 名称 | 第二十六章 解直角三角形 单元测试(含详解) 冀教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 523.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-18 20:32:21 | ||
图片预览



文档简介
第二十六章解直角三角形
综合素质评价
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.cos 45°的值为( )
A. B.1 C. D.
2.在Rt△ABC中,已知∠C=90°,AC=1,BC=3,则∠A的正切值为( )
A.3 B. C. D.
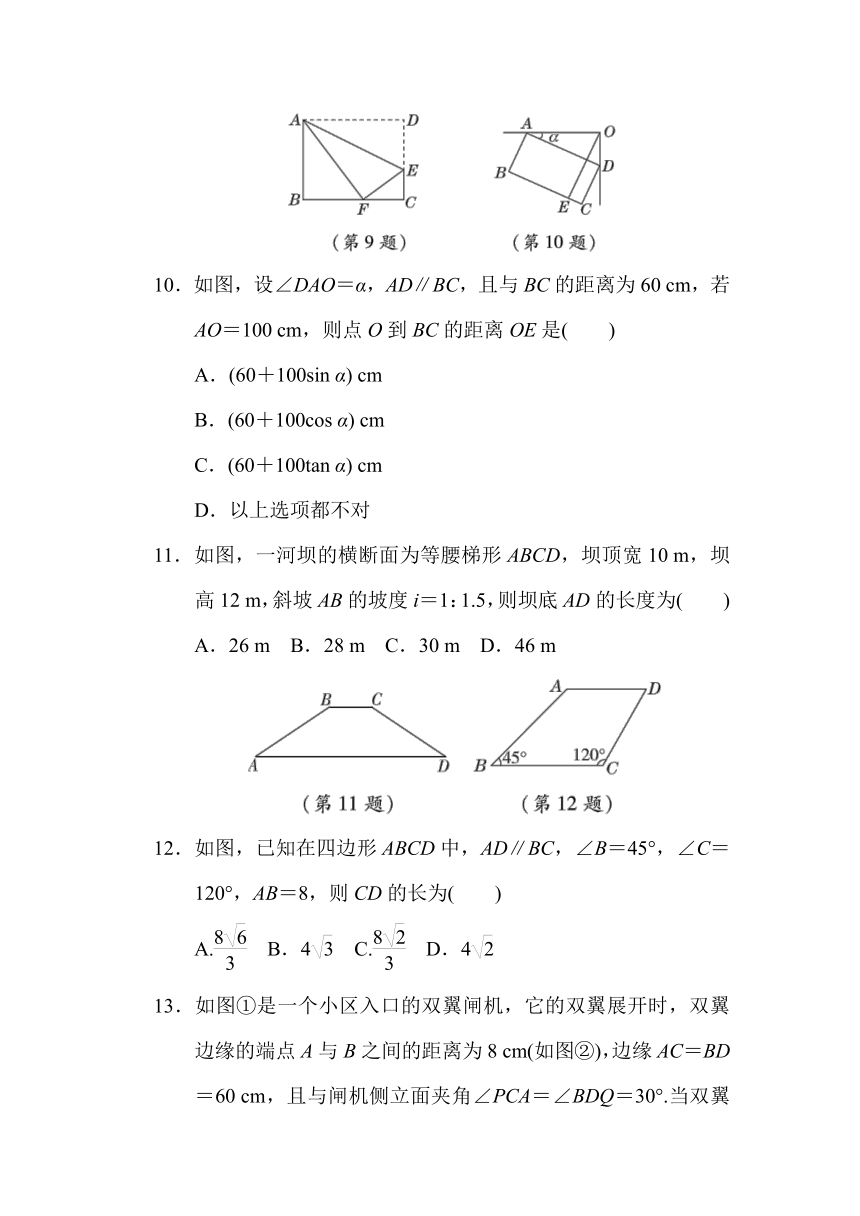
3.如图,若点A的坐标为(1,),则∠1=( )
A.30° B.45° C.60° D.75°
4.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
A. B. C. D.1
5.在△ABC中,若+=0,则∠C的度数是( )
A.45° B.60° C.90° D.105°
6.如图,在矩形ABCD中,AB=6,BC=8,分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N,作直线MN分别交AD,BC于点E,F,则AE的长为( )
A. B. C. D.
7.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,BC=8,AC=15,设∠BCD=α,则cos α的值为( )
A. B. C. D.
8.如图,某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距20 n mile.客轮以60 n mile/h的速度沿北偏西60°方向航行 h到达B处,那么tan∠ABP的值等于( )
A. B.2 C. D.
9.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知AB=4,BC=5,则cos∠EFC的值为( )
A. B. C. D.
10.如图,设∠DAO=α,AD∥BC,且与BC的距离为60 cm,若AO=100 cm,则点O到BC的距离OE是( )
A.(60+100sin α) cm
B.(60+100cos α) cm
C.(60+100tan α) cm
D.以上选项都不对
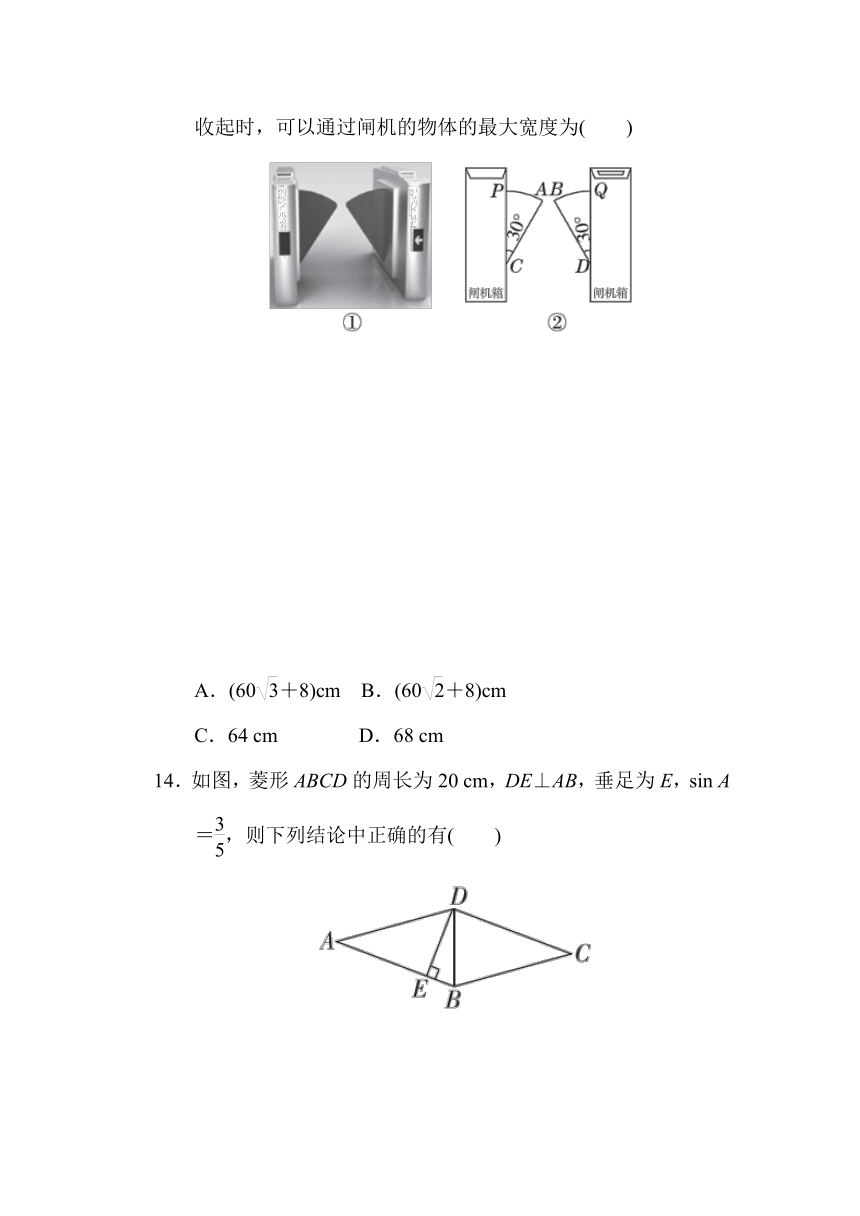
11.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10 m,坝高12 m,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )
A.26 m B.28 m C.30 m D.46 m
12.如图,已知在四边形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
A. B.4 C. D.4
13.如图①是一个小区入口的双翼闸机,它的双翼展开时,双翼边缘的端点A与B之间的距离为8 cm(如图②),边缘AC=BD=60 cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.(60+8)cm B.(60+8)cm
C.64 cm D.68 cm
14.如图,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sin A=,则下列结论中正确的有( )
①DE=3 cm;
②BE=1 cm;
③菱形的面积为15 cm2;
④BD=2 cm.
A.1个 B.2个 C.3个 D.4个
15.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( )
A.30° B.150°
C.60°或120° D.30°或150°
16.如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. B. C. D.3
二、填空题(17,19题每题3分,18题4分,共10分)
17.cos 60°+sin 45°+tan 30°=________.
18.如图,在△ABC中,sin B=,tan C=,AB=3,则AC的长为________,△ABC的面积为________.
19.我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么tan∠ADF=________.
三、解答题(20,21题每题8分,22~25题每题10分,26题12分,共68分)
20.计算:
(1)tan 30°cos 60°+tan 45°cos 30°;
(2)(-1)0++|-2|+tan 60°.
21.在△ABC中,∠C=90°.
(1)已知c=2,∠A=30°,求∠B,a,b;
(2)已知a=5,∠A=45°,求∠B,b,c.
22.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
(1)若∠A=60°,求BC的长;
(2)若sin A=,求AD的长.
23.如图①,“南天一柱”是张家界“三千奇峰”中的一座,位于世界自然遗产武陵源风景名胜区袁家界景区南端.如图②,航拍无人机以9 m/s的速度在空中向正东方向飞行,拍摄云海中的“南天一柱”美景.在A处测得“南天一柱”底部C的俯角为37°,继续飞行6 s到达B处,这时测得“南天一柱”底部C的俯角为45°,已知“南天一柱”的高为150 m,则这架航拍无人机继续向正东飞行是否安全?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
24.如图,湖边A,B两点由两段笔直的观景栈道AC和CB相连.为了计算A,B两点之间的距离,经测量得:∠BAC=37°,∠ABC=58°,AC=80米,求A,B两点之间的距离.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)
25.如图是由6个形状、大小完全相同的小矩形组成的,小矩形的顶点称为格点.已知小矩形较短的边长为1,△ABC的顶点都在格点上.
(1)用无刻度的直尺作图:找出格点D,连接CD,使∠ACD=90°;
(2)在(1)的条件下,连接AD,求tan ∠BAD的值.
26.如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面CQ,坡角∠QCN=30°.在阳光下,小明观察到AB在地面上的影长为120 cm,在坡面上的影长为180 cm.同一时刻,小明测得直立于地面长60 cm的木杆的影长为 90 cm(其影子完全落在地面上).求立柱AB的高度.
答案
一、1.C
2.A 【点拨】∵在Rt△ABC中,∠C=90°,AC=1,BC=3,∴∠A的正切值为==3.
3.C 【点拨】过点A作x轴的垂线,垂足为M.
∵点A的坐标为(1,),∴OM=1,AM=.
∵tan∠1===,∴∠1=60°.
4.B 【点拨】如图,过点A作BC的垂线,垂足为D.
在Rt△ABD中,AD=3,BD=4,则tan∠ABC==.
5.C 【点拨】∵+=0,
∴sinA=,cosB=,∴∠A=30°,∠B=60°,
∴∠C=180°-30°-60°=90°.
6.D 【点拨】设MN与AC的交点为O,
∵ 四边形ABCD为矩形,
∴∠ADC=90°,AB=DC=6,BC=AD=8,
∴AC===10,
∴cos∠CAD===.
又由作图知MN为AC的垂直平分线,
∴∠MOA=90°,AO=AC=5,
∴在Rt△AOE中,cos∠EAO=.
∵cos∠CAD=cos∠EAO,
∴=,∴AE=.
7.D 【点拨】根据勾股定理可知,AB==17.
由题易知∠BCD+∠B=90°,∠A+∠B=90°,
∴∠BCD=∠A=α.在Rt△ACB中,cosα==.
8.A 【点拨】∵灯塔A位于P的北偏东30°方向,且相距20 n mile,
∴AP=20 n mile.
∵客轮以60 n mile/h的速度沿北偏西60°方向航行 h到达B处,∴∠APB=90°,BP=60×=40(n mile),
∴tan∠ABP===.
9.D 【点拨】根据题意可得,AB=4,AF=AD=BC=5,
∠AFE=∠D=∠B=90°,
∴∠BAF+∠AFB=∠EFC+∠AFB。
∴∠BAF=∠EFC.
∴cos∠EFC=cos∠BAF==.
故选D.
10.A 【点拨】根据题意可得,O到AD的距离=100 sin α cm.
∵AD与BC的距离为60 cm,
∴OE=(60+100 sinα)cm.故选A.
11.D 【点拨】过点B作AD的垂线,垂足为E.
∵坝高12 m,斜坡AB的坡度i=1:1.5,
∴AE=1.5BE=18 m.
∵BC=10 m,∴易得AD=2AE+BC=2×18+10=46(m) .
12.D 点拨:过点A作AE⊥PC于点E,
过点B作BF⊥QD于点F,如图.
∵AC=60 cm,∠PCA=30°,∴AE=AC=30 cm.
同理可得BF=30 cm,
∴通过闸机的物体的最大宽度为30+8+30=68(cm).
故选D.
13.A 【点拨】如图,分别作AE⊥BC于E点,DF⊥BC,交BC的延长线于F点,则有AE=DF,sin B=sin 45°==,
∴DF=AE=AB=4.
∵∠DCF=180°-∠BCD=60°,∴sin∠DCF=sin 60°==,
∴CD===,故选A.
14.C 【点拨】∵菱形ABCD的周长为20 cm,
∴菱形的边长AB=AD=20÷4=5(cm).
∵DE⊥AB,sinA=,∴DE=5×=3(cm),故①正确;
∵AE===4(cm),
∴BE=AB-AE=5-4=1(cm),故②正确;
菱形的面积=AB·DE=5×3=15(cm2),故③正确;
在Rt△BDE中,BD===(cm),故④错误,
综上所述,正确的有①②③共3个.
15.D 【点拨】有两种情况:当顶角为锐角时,如图①,sin A=,则∠A=30°;当顶角为钝角时,如图②,sin (180°-∠BAC)=,则180°-∠BAC=30°,所以∠BAC=150°.
16.C 【点拨】∵P点坐标为(1,1),
∴OP与x轴正方向的夹角为45°.
又∵OP∥AB,∴∠BAO=45°.
∴△OAB为等腰直角三角形,∴OA=OB.
设OC=x,则BC=2OC=2x,∴OB=OA=3x,
∴tan∠OAP===.
二、17.2 【点拨】原式=+×+×=2.
18.; 【点拨】如图,过A作AD⊥BC.
在Rt△ABD中,sinB=,AB=3,
∴AD=AB·sinB=1,
∴BD===2.
在Rt△ACD中,tanC=,
∴=,即CD=.
∴BC=BD+CD=3,
AC===.
∴S△ABC=BC·AD=.
19. 【点拨】∵大正方形ABCD的面积是100,
∴AD=10.
∵小正方形EFGH的面积是4,
∴小正方形EFGH的边长为2,
∴易得DF-AF=2.
设AF=x,则DF=x+2.
由勾股定理得,x2+(x+2)2=102,
解得x=6或-8(负值舍去),
∴AF=6,DF=8,∴tan∠ADF===.
三、20.【解】(1)原式=×+1×=+=.
(2)原式=1+9+2-+=12.
21.【解】(1)∵∠C=90°,∠A=30°,∴∠B=60°.
∵sin A=,sin B=,
∴a=c·sin A=2×=,
b=c·sin B=2×=3.
(2)∵∠C=90°,∠A=45°,∴∠B=45°.
∴b=a=5.
∴c==10.
22.【解】(1)在Rt△ABE中,
∵∠A=60°,∠ABE=90°,AB=6,tan A=,
∴∠E=30°,BE=AB·tan A=6×tan 60°=6.
在Rt△CDE中,
∵CD=4,sin E=,∠E=30°,
∴CE===8.
∴BC=BE-CE=6-8.
(2)∵在Rt△ABE中,sin A==,
∴可设BE=4x(x>0),则AE=5x.
由勾股定理可得AB=3x,
又∵AB=6,∴3x=6,解得x=2.
∴BE=8,AE=10.
∴tan E====,解得DE=.
∴AD=AE-DE=10-=.
23.【解】设直线AB与“南天一柱”所在直线相交于点D,如图.由题意得∠CAD=37°,∠CBD=45°.设CD=x m.
在Rt△ACD中,
∵tan∠CAD==≈0.75,
∴AD≈x m.
在Rt△BCD中,
∵tan∠CBD===1,
∴BD=x m.
∵AD-BD=AB,
∴x-x≈9×6,∴x≈162.
∵162>150,
∴这架航拍无人机继续向正东飞行安全.
24.【解】如图,过点C作CD⊥AB,垂足为点D,
在Rt△ACD中,
∵∠DAC=37°,AC=80米,
sin∠DAC=,cos∠DAC=,
∴CD=AC·sin37°≈80×0.60=48(米),
AD=AC·cos37°≈80×0.80=64(米),
在Rt△BCD中,
∵∠CBD=58°,CD=48米,tan∠CBD=,
∴BD=≈=30(米),
∴AB=AD+BD≈64+30=94(米).
答:A,B两点之间的距离约为94米.
25.【解】(1)如图所示,点D即为所求.
(2)如图,连接BD.
∵∠BED=90°,BE=DE=1,
∴∠EBD=∠EDB=45°,
BD===.
易知BF=AF=2,∠BFA=90°,∴∠ABF=∠BAF=45°,AB===2 .
∴∠ABD=∠ABF+∠EBD=45°+45°=90°.
∴tan ∠BAD===.
26.【解】如图,延长AD交BN于点E,
过点D作DF⊥BN于点F,
在Rt△CDF中,∠CFD=90°,∠DCF=30°,
∴DF=CD=90 cm,CF=CD·cos∠DCF=180×=90(cm).
由题意得=,即=,
解得EF=135 cm,
∴BE=BC+CF+EF=120+90+135=(255+90)cm,
由题意得=,
∴=,
解得AB=(170+60)cm.
答:立柱AB的高度为(170+60)cm.
综合素质评价
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.cos 45°的值为( )
A. B.1 C. D.
2.在Rt△ABC中,已知∠C=90°,AC=1,BC=3,则∠A的正切值为( )
A.3 B. C. D.
3.如图,若点A的坐标为(1,),则∠1=( )
A.30° B.45° C.60° D.75°
4.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
A. B. C. D.1
5.在△ABC中,若+=0,则∠C的度数是( )
A.45° B.60° C.90° D.105°
6.如图,在矩形ABCD中,AB=6,BC=8,分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N,作直线MN分别交AD,BC于点E,F,则AE的长为( )
A. B. C. D.
7.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,BC=8,AC=15,设∠BCD=α,则cos α的值为( )
A. B. C. D.
8.如图,某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距20 n mile.客轮以60 n mile/h的速度沿北偏西60°方向航行 h到达B处,那么tan∠ABP的值等于( )
A. B.2 C. D.
9.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知AB=4,BC=5,则cos∠EFC的值为( )
A. B. C. D.
10.如图,设∠DAO=α,AD∥BC,且与BC的距离为60 cm,若AO=100 cm,则点O到BC的距离OE是( )
A.(60+100sin α) cm
B.(60+100cos α) cm
C.(60+100tan α) cm
D.以上选项都不对
11.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10 m,坝高12 m,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )
A.26 m B.28 m C.30 m D.46 m
12.如图,已知在四边形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
A. B.4 C. D.4
13.如图①是一个小区入口的双翼闸机,它的双翼展开时,双翼边缘的端点A与B之间的距离为8 cm(如图②),边缘AC=BD=60 cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A.(60+8)cm B.(60+8)cm
C.64 cm D.68 cm
14.如图,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sin A=,则下列结论中正确的有( )
①DE=3 cm;
②BE=1 cm;
③菱形的面积为15 cm2;
④BD=2 cm.
A.1个 B.2个 C.3个 D.4个
15.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( )
A.30° B.150°
C.60°或120° D.30°或150°
16.如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. B. C. D.3
二、填空题(17,19题每题3分,18题4分,共10分)
17.cos 60°+sin 45°+tan 30°=________.
18.如图,在△ABC中,sin B=,tan C=,AB=3,则AC的长为________,△ABC的面积为________.
19.我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么tan∠ADF=________.
三、解答题(20,21题每题8分,22~25题每题10分,26题12分,共68分)
20.计算:
(1)tan 30°cos 60°+tan 45°cos 30°;
(2)(-1)0++|-2|+tan 60°.
21.在△ABC中,∠C=90°.
(1)已知c=2,∠A=30°,求∠B,a,b;
(2)已知a=5,∠A=45°,求∠B,b,c.
22.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
(1)若∠A=60°,求BC的长;
(2)若sin A=,求AD的长.
23.如图①,“南天一柱”是张家界“三千奇峰”中的一座,位于世界自然遗产武陵源风景名胜区袁家界景区南端.如图②,航拍无人机以9 m/s的速度在空中向正东方向飞行,拍摄云海中的“南天一柱”美景.在A处测得“南天一柱”底部C的俯角为37°,继续飞行6 s到达B处,这时测得“南天一柱”底部C的俯角为45°,已知“南天一柱”的高为150 m,则这架航拍无人机继续向正东飞行是否安全?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
24.如图,湖边A,B两点由两段笔直的观景栈道AC和CB相连.为了计算A,B两点之间的距离,经测量得:∠BAC=37°,∠ABC=58°,AC=80米,求A,B两点之间的距离.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)
25.如图是由6个形状、大小完全相同的小矩形组成的,小矩形的顶点称为格点.已知小矩形较短的边长为1,△ABC的顶点都在格点上.
(1)用无刻度的直尺作图:找出格点D,连接CD,使∠ACD=90°;
(2)在(1)的条件下,连接AD,求tan ∠BAD的值.
26.如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面CQ,坡角∠QCN=30°.在阳光下,小明观察到AB在地面上的影长为120 cm,在坡面上的影长为180 cm.同一时刻,小明测得直立于地面长60 cm的木杆的影长为 90 cm(其影子完全落在地面上).求立柱AB的高度.
答案
一、1.C
2.A 【点拨】∵在Rt△ABC中,∠C=90°,AC=1,BC=3,∴∠A的正切值为==3.
3.C 【点拨】过点A作x轴的垂线,垂足为M.
∵点A的坐标为(1,),∴OM=1,AM=.
∵tan∠1===,∴∠1=60°.
4.B 【点拨】如图,过点A作BC的垂线,垂足为D.
在Rt△ABD中,AD=3,BD=4,则tan∠ABC==.
5.C 【点拨】∵+=0,
∴sinA=,cosB=,∴∠A=30°,∠B=60°,
∴∠C=180°-30°-60°=90°.
6.D 【点拨】设MN与AC的交点为O,
∵ 四边形ABCD为矩形,
∴∠ADC=90°,AB=DC=6,BC=AD=8,
∴AC===10,
∴cos∠CAD===.
又由作图知MN为AC的垂直平分线,
∴∠MOA=90°,AO=AC=5,
∴在Rt△AOE中,cos∠EAO=.
∵cos∠CAD=cos∠EAO,
∴=,∴AE=.
7.D 【点拨】根据勾股定理可知,AB==17.
由题易知∠BCD+∠B=90°,∠A+∠B=90°,
∴∠BCD=∠A=α.在Rt△ACB中,cosα==.
8.A 【点拨】∵灯塔A位于P的北偏东30°方向,且相距20 n mile,
∴AP=20 n mile.
∵客轮以60 n mile/h的速度沿北偏西60°方向航行 h到达B处,∴∠APB=90°,BP=60×=40(n mile),
∴tan∠ABP===.
9.D 【点拨】根据题意可得,AB=4,AF=AD=BC=5,
∠AFE=∠D=∠B=90°,
∴∠BAF+∠AFB=∠EFC+∠AFB。
∴∠BAF=∠EFC.
∴cos∠EFC=cos∠BAF==.
故选D.
10.A 【点拨】根据题意可得,O到AD的距离=100 sin α cm.
∵AD与BC的距离为60 cm,
∴OE=(60+100 sinα)cm.故选A.
11.D 【点拨】过点B作AD的垂线,垂足为E.
∵坝高12 m,斜坡AB的坡度i=1:1.5,
∴AE=1.5BE=18 m.
∵BC=10 m,∴易得AD=2AE+BC=2×18+10=46(m) .
12.D 点拨:过点A作AE⊥PC于点E,
过点B作BF⊥QD于点F,如图.
∵AC=60 cm,∠PCA=30°,∴AE=AC=30 cm.
同理可得BF=30 cm,
∴通过闸机的物体的最大宽度为30+8+30=68(cm).
故选D.
13.A 【点拨】如图,分别作AE⊥BC于E点,DF⊥BC,交BC的延长线于F点,则有AE=DF,sin B=sin 45°==,
∴DF=AE=AB=4.
∵∠DCF=180°-∠BCD=60°,∴sin∠DCF=sin 60°==,
∴CD===,故选A.
14.C 【点拨】∵菱形ABCD的周长为20 cm,
∴菱形的边长AB=AD=20÷4=5(cm).
∵DE⊥AB,sinA=,∴DE=5×=3(cm),故①正确;
∵AE===4(cm),
∴BE=AB-AE=5-4=1(cm),故②正确;
菱形的面积=AB·DE=5×3=15(cm2),故③正确;
在Rt△BDE中,BD===(cm),故④错误,
综上所述,正确的有①②③共3个.
15.D 【点拨】有两种情况:当顶角为锐角时,如图①,sin A=,则∠A=30°;当顶角为钝角时,如图②,sin (180°-∠BAC)=,则180°-∠BAC=30°,所以∠BAC=150°.
16.C 【点拨】∵P点坐标为(1,1),
∴OP与x轴正方向的夹角为45°.
又∵OP∥AB,∴∠BAO=45°.
∴△OAB为等腰直角三角形,∴OA=OB.
设OC=x,则BC=2OC=2x,∴OB=OA=3x,
∴tan∠OAP===.
二、17.2 【点拨】原式=+×+×=2.
18.; 【点拨】如图,过A作AD⊥BC.
在Rt△ABD中,sinB=,AB=3,
∴AD=AB·sinB=1,
∴BD===2.
在Rt△ACD中,tanC=,
∴=,即CD=.
∴BC=BD+CD=3,
AC===.
∴S△ABC=BC·AD=.
19. 【点拨】∵大正方形ABCD的面积是100,
∴AD=10.
∵小正方形EFGH的面积是4,
∴小正方形EFGH的边长为2,
∴易得DF-AF=2.
设AF=x,则DF=x+2.
由勾股定理得,x2+(x+2)2=102,
解得x=6或-8(负值舍去),
∴AF=6,DF=8,∴tan∠ADF===.
三、20.【解】(1)原式=×+1×=+=.
(2)原式=1+9+2-+=12.
21.【解】(1)∵∠C=90°,∠A=30°,∴∠B=60°.
∵sin A=,sin B=,
∴a=c·sin A=2×=,
b=c·sin B=2×=3.
(2)∵∠C=90°,∠A=45°,∴∠B=45°.
∴b=a=5.
∴c==10.
22.【解】(1)在Rt△ABE中,
∵∠A=60°,∠ABE=90°,AB=6,tan A=,
∴∠E=30°,BE=AB·tan A=6×tan 60°=6.
在Rt△CDE中,
∵CD=4,sin E=,∠E=30°,
∴CE===8.
∴BC=BE-CE=6-8.
(2)∵在Rt△ABE中,sin A==,
∴可设BE=4x(x>0),则AE=5x.
由勾股定理可得AB=3x,
又∵AB=6,∴3x=6,解得x=2.
∴BE=8,AE=10.
∴tan E====,解得DE=.
∴AD=AE-DE=10-=.
23.【解】设直线AB与“南天一柱”所在直线相交于点D,如图.由题意得∠CAD=37°,∠CBD=45°.设CD=x m.
在Rt△ACD中,
∵tan∠CAD==≈0.75,
∴AD≈x m.
在Rt△BCD中,
∵tan∠CBD===1,
∴BD=x m.
∵AD-BD=AB,
∴x-x≈9×6,∴x≈162.
∵162>150,
∴这架航拍无人机继续向正东飞行安全.
24.【解】如图,过点C作CD⊥AB,垂足为点D,
在Rt△ACD中,
∵∠DAC=37°,AC=80米,
sin∠DAC=,cos∠DAC=,
∴CD=AC·sin37°≈80×0.60=48(米),
AD=AC·cos37°≈80×0.80=64(米),
在Rt△BCD中,
∵∠CBD=58°,CD=48米,tan∠CBD=,
∴BD=≈=30(米),
∴AB=AD+BD≈64+30=94(米).
答:A,B两点之间的距离约为94米.
25.【解】(1)如图所示,点D即为所求.
(2)如图,连接BD.
∵∠BED=90°,BE=DE=1,
∴∠EBD=∠EDB=45°,
BD===.
易知BF=AF=2,∠BFA=90°,∴∠ABF=∠BAF=45°,AB===2 .
∴∠ABD=∠ABF+∠EBD=45°+45°=90°.
∴tan ∠BAD===.
26.【解】如图,延长AD交BN于点E,
过点D作DF⊥BN于点F,
在Rt△CDF中,∠CFD=90°,∠DCF=30°,
∴DF=CD=90 cm,CF=CD·cos∠DCF=180×=90(cm).
由题意得=,即=,
解得EF=135 cm,
∴BE=BC+CF+EF=120+90+135=(255+90)cm,
由题意得=,
∴=,
解得AB=(170+60)cm.
答:立柱AB的高度为(170+60)cm.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
