山东省菏泽市东明县2025届九年级下学期中考二模数学试卷(含答案)
文档属性
| 名称 | 山东省菏泽市东明县2025届九年级下学期中考二模数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-18 20:22:05 | ||
图片预览


文档简介
2025年山东省菏泽市东明县中考二模数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个数中,最小的数是( )
A. B.0 C.3 D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.如图为一个弯折的铁丝,,工人师傅对该铁丝进一步加工,在处进行第二次弯折,最终保证弯折后的部分与保持平行,那么弯折后形成的( )
A. B.
C. D.或
5.烷烃是一类由碳、氢元素组成的有机化合物质,下图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子.第1种如图①有4个氢原子,第2种如图②有6个氢原子,第3种如图③有8个氢原子,……按照这一规律,第10种化合物的分子结构模型中氢原子的个数是( )
A.20 B.22 C.24 D.26
6.已知点P(x-2,6-2x)是平面直角坐标系第二象限内一点,则x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7.我国古代《四元玉鉴》中记载“二果问价”问题,其内容大致如下:用九百九十九文钱,可买甜果苦果共一千个,若…,…,试问买甜苦果各几个?若设买甜果x个,买苦果y个,列出符合题意的二元一次方程组:.根据已有信息,题中用“…,…”表示的缺失的条件应为( )
A.甜果七个用四文钱,苦果九个用十一文钱
B.甜果十一个用九文钱,苦果四个用七文钱
C.甜果四个用七文钱,苦果十一个用九文钱
D.甜果九个用十一文钱,苦果七个用四文钱
8.为了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,班主任对全班50名同学进行了问卷调查(每名同学只选其中的一类),依据50份问卷调查结果绘制了全班同学喜爱节目情况扇形统计图(如图所示).下列说法正确的是( )
A.班主任采用的是抽样调查 B.喜爱动画节目的同学最多
C.喜爱戏曲节目的同学有6名 D.“体育”对应扇形的圆心角为
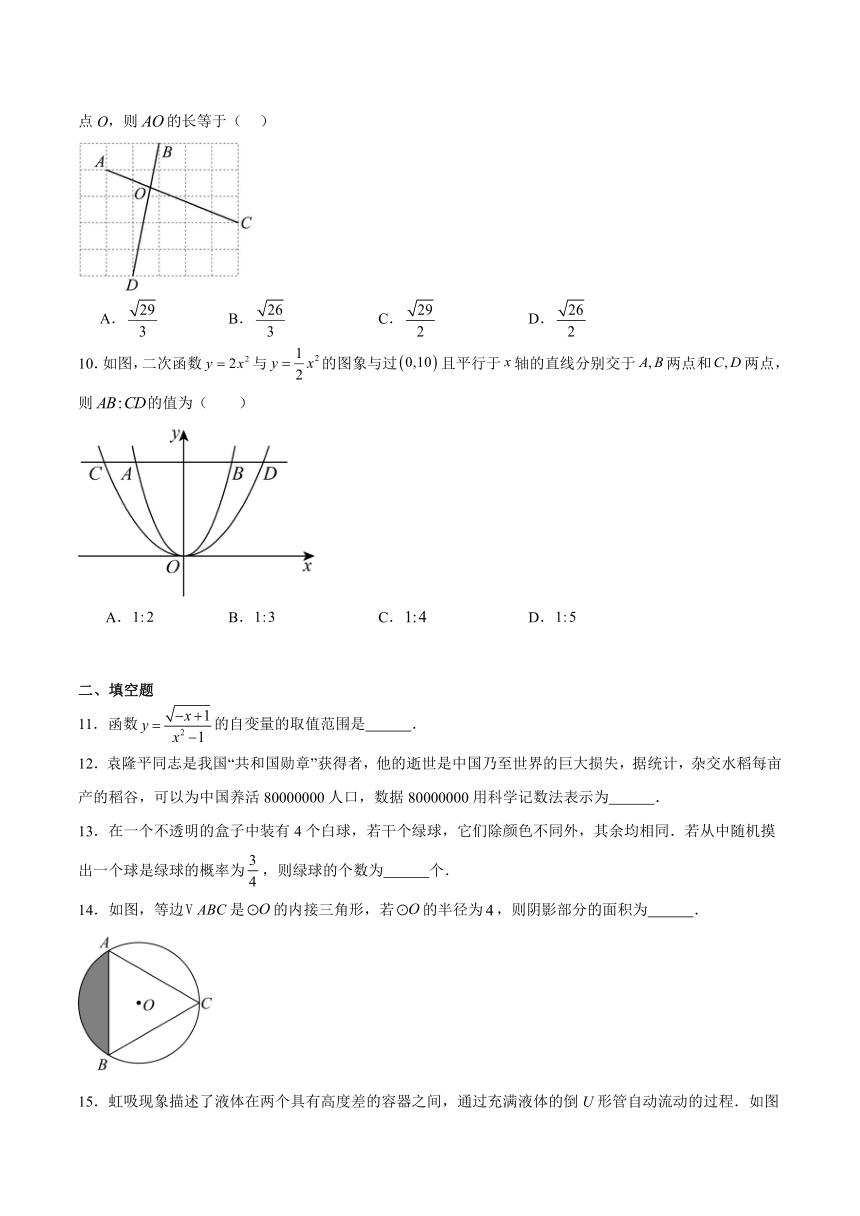
9.如图,在边长为1的小正方形组成的网格中,点A,B,C,D在小正方形的顶点处,与相交于点O,则的长等于( )
A. B. C. D.
10.如图,二次函数与的图象与过且平行于轴的直线分别交于两点和两点,则的值为( )
A. B. C. D.
二、填空题
11.函数的自变量的取值范围是 .
12.袁隆平同志是我国“共和国勋章”获得者,他的逝世是中国乃至世界的巨大损失,据统计,杂交水稻每亩产的稻谷,可以为中国养活80000000人口,数据80000000用科学记数法表示为 .
13.在一个不透明的盒子中装有4个白球,若干个绿球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是绿球的概率为,则绿球的个数为 个.
14.如图,等边是的内接三角形,若的半径为,则阴影部分的面积为 .
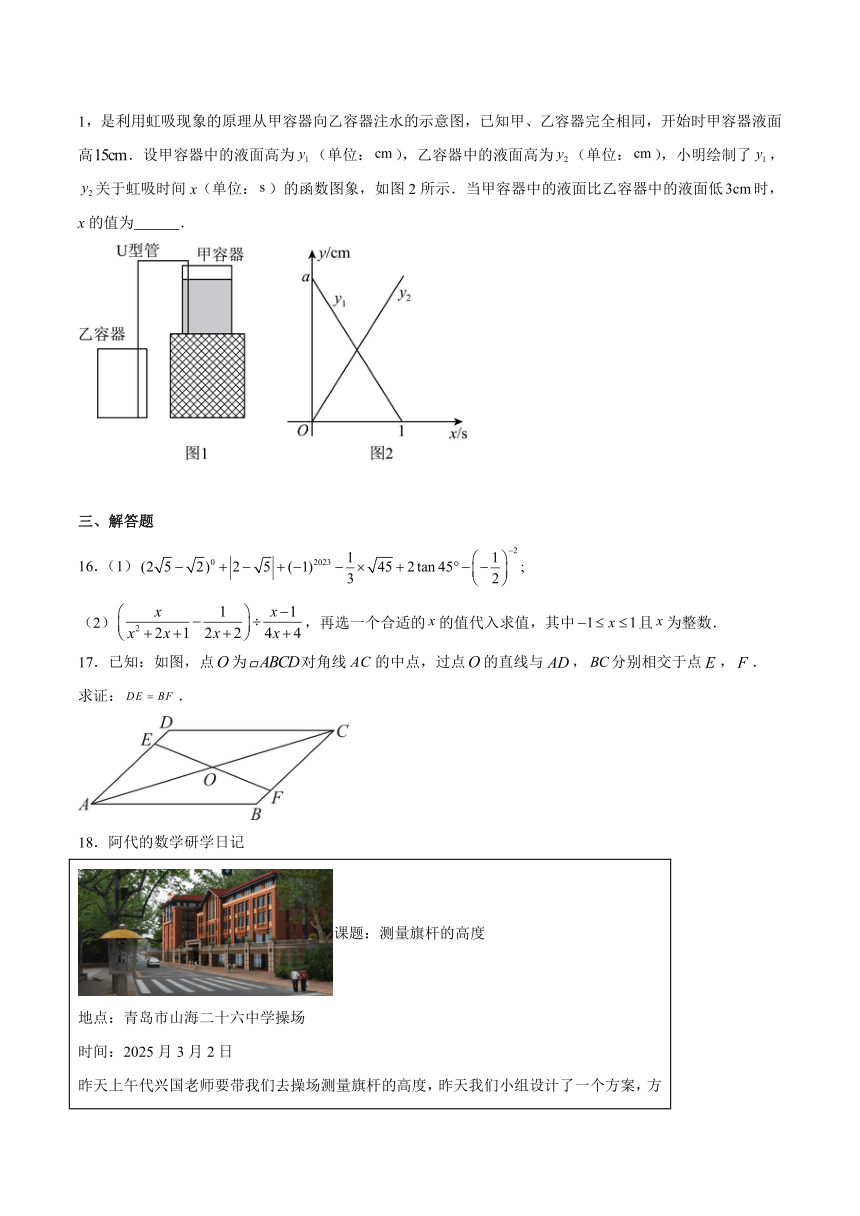
15.虹吸现象描述了液体在两个具有高度差的容器之间,通过充满液体的倒U形管自动流动的过程.如图1,是利用虹吸现象的原理从甲容器向乙容器注水的示意图,已知甲、乙容器完全相同,开始时甲容器液面高.设甲容器中的液面高为(单位:),乙容器中的液面高为(单位:),小明绘制了,关于虹吸时间x(单位:)的函数图象,如图2所示.当甲容器中的液面比乙容器中的液面低时,x的值为 .
三、解答题
16.(1)
(2),再选一个合适的的值代入求值,其中且为整数.
17.已知:如图,点为对角线的中点,过点的直线与,分别相交于点,.
求证:.
18.阿代的数学研学日记
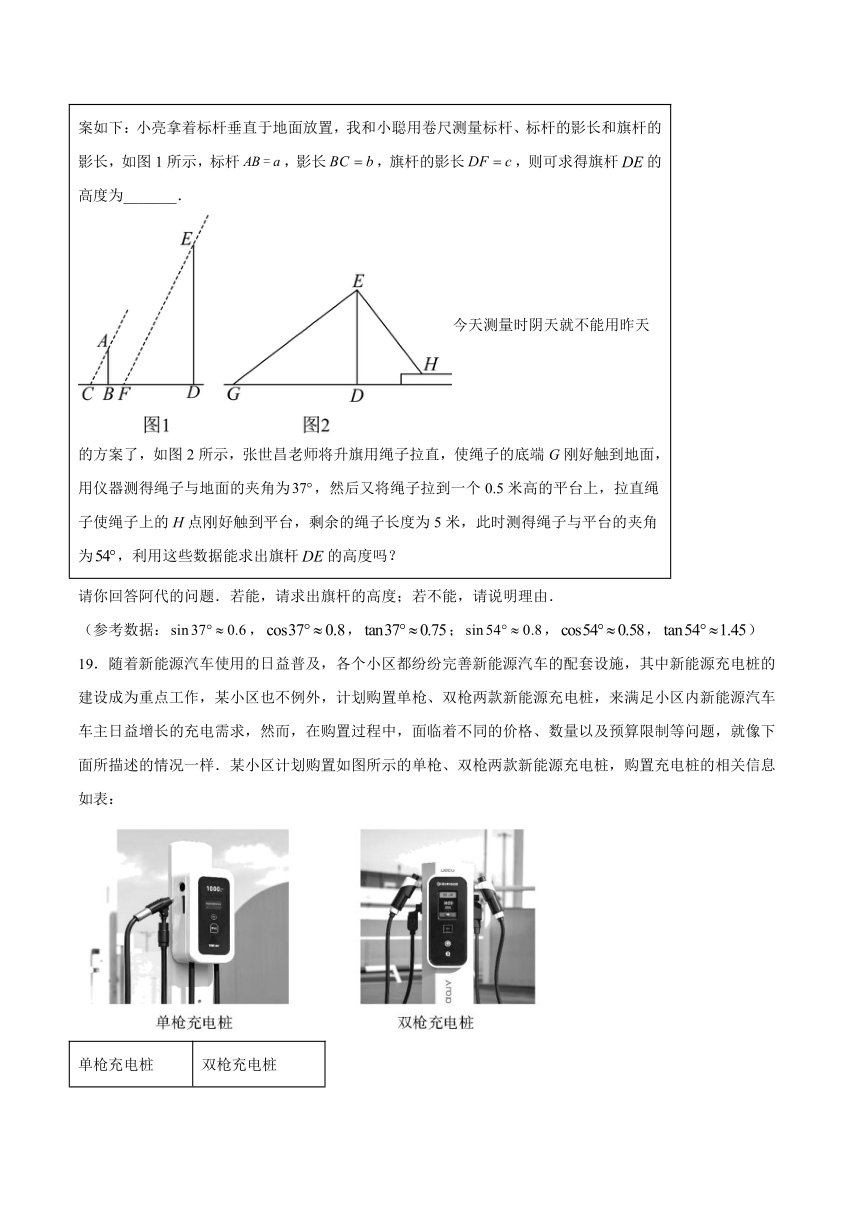
课题:测量旗杆的高度 地点:青岛市山海二十六中学操场 时间:2025月3月2日 昨天上午代兴国老师要带我们去操场测量旗杆的高度,昨天我们小组设计了一个方案,方案如下:小亮拿着标杆垂直于地面放置,我和小聪用卷尺测量标杆、标杆的影长和旗杆的影长,如图1所示,标杆,影长,旗杆的影长,则可求得旗杆的高度为_______. 今天测量时阴天就不能用昨天的方案了,如图2所示,张世昌老师将升旗用绳子拉直,使绳子的底端G刚好触到地面,用仪器测得绳子与地面的夹角为,然后又将绳子拉到一个0.5米高的平台上,拉直绳子使绳子上的H点刚好触到平台,剩余的绳子长度为5米,此时测得绳子与平台的夹角为,利用这些数据能求出旗杆的高度吗?
请你回答阿代的问题.若能,请求出旗杆的高度;若不能,请说明理由.
(参考数据:,,;,,)
19.随着新能源汽车使用的日益普及,各个小区都纷纷完善新能源汽车的配套设施,其中新能源充电桩的建设成为重点工作,某小区也不例外,计划购置单枪、双枪两款新能源充电桩,来满足小区内新能源汽车车主日益增长的充电需求,然而,在购置过程中,面临着不同的价格、数量以及预算限制等问题,就像下面所描述的情况一样.某小区计划购置如图所示的单枪、双枪两款新能源充电桩,购置充电桩的相关信息如表:
单枪充电桩 双枪充电桩
花费:元 花费:元
单价:元/个 单价:元/个
(1)若本次购买单枪充电桩的数量比双枪充电桩的数量多个,求单枪、双枪两款新能源充电桩的单价;
(2)在(1)的条件下,根据居民需求,小区决定再次购进单枪、双枪两款新能源充电桩共个,已知单枪新能源充电桩的单价比上次购买时提高了,双枪新能源充电桩的单价比上次购买时降低了,如果此次加购小区预备支出不超过元,求小区最少需要购买单枪新能源充电桩的数量.
20.2022年10月16日至10月22日,中国共产党第二十次全国代表大会在北京召开.为激励青少年争做党的事业接班人,某市团市委在党史馆组织了“红心永向党”为主题的知识竞赛,依据得分情况将获奖结果分为四个等级:A级为特等奖,B级为一等奖,C级为二等奖,D级为优秀奖.并将统计结果绘制成了如图所示的两幅不完整的统计图.
请根据相关信息解答下列问题:
(1)本次竞赛共有______名选手获奖,扇形统计图中扇形C的圆心角度数是______度;
(2)补全条形统计图;
(3)若该党史馆有一个入口,三个出口.请用树状图或列表法,求参赛选手小丽和小颖由馆内恰好从同一出口走出的概率.
21.中,,点在上,以为半径的圆交于点,交于点.且.
(1)求证:是的切线.
(2)连接交于点,若,求弧的长.
22.如图,在直角三角形中,,,,动点以个单位每秒的速度沿的线路运动,交于点.设运动时间为秒,三角形的周长记为,与的比值记为.
(1)请直接写出、分别关于的函数表达式,并注明的取值范围;
(2)在给定的平面直角坐标系中画出函数,的图象;
(3)请结合函数图象,直接写出时的取值范围.(近似值保留一位小数,误差不超过0.2).
23.如图1,在平面直角坐标系中,抛物线与x轴交于两点,B(点A在B左边),交y轴于C,点是抛物线上一点.
(1)求抛物线的关系式;
(2)在对称轴上找一点M,使的值最小,求点M的坐标;
(3)如图2,抛物线上是否存在点Q,使?若存在,请求出点Q的坐标;若不存在,请说明理由.
《2025年山东省菏泽市东明县中考二模数学试题 》参考答案
1.A
解:∵,
∴最小的数是;
故选:A.
2.B
解:A、是轴对称图形而不是中心对称图形;
B、既是轴对称图形也是中心对称图形;
C、是轴对称图形而不是中心对称图形;
D、是轴对称图形而不是中心对称图形;
故选:B.
3.D
根据合并同类项法则、完全平方公式、积的乘方、单项式乘多项式法则进行计算即可.
解:A、与不是同类项,不能合并,故不符合题意;
B、,故不符合题意;
C、,故不符合题意;
D、,故符合题意;
故选:D.
4.D
解:根据平行线的性质,当点在点左侧时,,
当点在点右侧时,,
故选:D.
5.B
解:由图可得,
第1种如图①有4个氢原子,即,
第2种如图②有6个氢原子,即,
第3种如图③有8个氢原子,即,
,
第10种化合物的分子结构模型中氢原子的个数是:;
故选:B.
6.C
解:由题意得:
,
解得:,
则在数轴上表示为;
故选C.
7.D
解:根据,可得甜果九个用十一文钱,苦果七个用四文钱,
故选:D
8.D
全班共50名学生,班主任制作了50份问卷调查,
所以班主任采用的是全面调查,
故A选项错误;
喜爱娱乐节目的同学所占的百分比最多,因此喜爱娱乐节目的同学最多,
故B选项错误;
喜爱戏曲节目的同学有名,
故C选项错误;
“体育”对应扇形的圆心角为,
故D选项正确.
故选:D.
9.A
连接,,并标注字母如图所示.
根据题意可知,,,,
∵,,
∴∽,
∴,,
∴,
∴,
∴∽,
∴,
∴.
根据勾股定理,得,
∴.
故选:A.
10.A
根据题意:,
解得:,
,
,
根据题意得:,
解得:,
,
,
故选:A.
11.且
解:∵函数有意义,
∴自变量的取值范围为,
解得:且,
故答案为:且.
12.
解:80000000用科学记数法表示为.
故答案为:.
13.12
解:设绿球的个数为x个,则这个不透明的盒子中共装有个球,
根据题意得:,
解得:,
经检验,是方程的解,
∴绿球的个数为12个.
故答案为:12.
14.
解:连接、,连接并延长并于点,如下图,
则.
等边是的内接三角形,
,
,,
,,
,
,
图中阴影部分的面积.
故答案为:.
15./
解:当时,,
∵开始时甲容器液面高,
∴,
又∵时,,
∴设,
将代入得,解得,
∴,
∵甲容器向乙容器注水,始终有,
∴,
∴甲容器中的液面比乙容器中的液面低时,即,
∴,
解得,
故答案为:.
16.(1);(2),时,原式.
(1)解:原式;
(2)解:原式,
要是分式有意义,则,
,原式.
17.详见解析
证明:∵四边形是平行四边形,
∴,,
∴,,
∵点为对角线的中点,
∴,
∴,
∴,
∴,
∴.
18.;旗杆高度可求,为米
(1)解:因为,
所以,
所以,
所以,
所以,
所以;
(2)如图所示,过点H,作于N,
设米,
米,
在中,,
,
在中,,,
,
,
,
解得:,
答:旗杆高度可求,为米.
19.(1)单枪新能源充电桩的价格为1000元/个,双枪新能源充电桩的价格为1500元/个
(2)小区最少需要购买单枪新能源充电桩8个
(1)解:根据题意可得
解得:
经检验,是原方程的解,且符合题意,
(元/个)
答:单枪新能源充电桩的价格为1000元/个,双枪新能源充电桩的价格为1500元/个;
(2)解:单枪新能源充电桩的单价比上次购买时提高了,则现在单枪新能源充电桩的单价为(元/个)
双枪新能源充电桩的单价比上次购买时降低了,则现在双枪新能源充电桩的单价为(元/个)
设再次购进单枪新能源允电社个,则购进双枪新能源允电社个,总花费为元
∵此次加购小区预备支出不超过元
∴
解得
∴的最小值为
答:小区最少需要购买单枪新能源充电桩8个.
20.(1)200,108
(2)见解析
(3)
(1)解:名,
∴本次竞赛共有200名选手获奖,
∴C级的人数为名,
∴扇形统计图中扇形C的圆心角度数是度,
故答案为:200,108;
(2)解:B级的人数为名,
补全统计图如下:
(3)解:设这三个出口分别用E、F、G表示,列表如下:
E F G
E (E,E) (F,E) (G,E)
F (E,F) (F,F) (G,F)
G (E,G) (F,G) (G,G)
由表格可知一共有9种等可能性的结果数,其中参赛选手小丽和小颖由馆内恰好从同一出口走出的结果数有3种,
∴参赛选手小丽和小颖由馆内恰好从同一出口走出的概率.
21.(1)见解析
(2)弧的长为.
(1)证明:连接,
在和中,,
∴,
∴,
∵为的半径,
∴是的切线;
(2)解:∵,
∴,
设的半径为,
在中,,即,
解得,
∴,,,
∴,
∵,
∴,
∴弧的长为.
22.(1),
(2)见解析
(3)当时的取值范围为
(1)解:∵,,,
∴,
∴,,
∵,
∴在中,,,
∴,,
∴,,
∴,;
(2)解:依题意,列表:
0 1 2 5 6
0
10 5 2
描点,连线,函数图象如图所示,
(3)解:由图象得,当时的取值范围为.
23.(1)
(2)
(3)存在,或
(1)将点,代入,
得: ,
解得:
∴抛物线的解析式为 ;
(2)当时,,
∴点,
当时,有,
解得:,,
∴点,
∴抛物线的对称轴为:直线
设直线的关系式为,把点B坐标代入,
得:,解得,,
∴直线的关系式为,
由对称可得,直线与对称轴交点就是所求的点M,
当时,,
∴时,最小;
(3)当Q在下方时,如图,过P作于H,过H作轴, 交y轴于M,过P作于N,
∴,
∵,
∴是等腰直角三角形,
∴,
∴,
∴,
∴,
∴,,
∵,
∵,,
∴,解得 ,
∴,
设直线的解析式为 ,
∴,解得,
∴直线的解析式为 ,
联立直线与抛物线解析式得
,
解得或 ,
∴;
②当Q在上方时, 如图,过P作.于H,过H作.轴, 交y轴于M,过P作于N,
同理得.
综上,存在,点Q的坐标为或
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个数中,最小的数是( )
A. B.0 C.3 D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.如图为一个弯折的铁丝,,工人师傅对该铁丝进一步加工,在处进行第二次弯折,最终保证弯折后的部分与保持平行,那么弯折后形成的( )
A. B.
C. D.或
5.烷烃是一类由碳、氢元素组成的有机化合物质,下图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子.第1种如图①有4个氢原子,第2种如图②有6个氢原子,第3种如图③有8个氢原子,……按照这一规律,第10种化合物的分子结构模型中氢原子的个数是( )
A.20 B.22 C.24 D.26
6.已知点P(x-2,6-2x)是平面直角坐标系第二象限内一点,则x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7.我国古代《四元玉鉴》中记载“二果问价”问题,其内容大致如下:用九百九十九文钱,可买甜果苦果共一千个,若…,…,试问买甜苦果各几个?若设买甜果x个,买苦果y个,列出符合题意的二元一次方程组:.根据已有信息,题中用“…,…”表示的缺失的条件应为( )
A.甜果七个用四文钱,苦果九个用十一文钱
B.甜果十一个用九文钱,苦果四个用七文钱
C.甜果四个用七文钱,苦果十一个用九文钱
D.甜果九个用十一文钱,苦果七个用四文钱
8.为了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,班主任对全班50名同学进行了问卷调查(每名同学只选其中的一类),依据50份问卷调查结果绘制了全班同学喜爱节目情况扇形统计图(如图所示).下列说法正确的是( )
A.班主任采用的是抽样调查 B.喜爱动画节目的同学最多
C.喜爱戏曲节目的同学有6名 D.“体育”对应扇形的圆心角为
9.如图,在边长为1的小正方形组成的网格中,点A,B,C,D在小正方形的顶点处,与相交于点O,则的长等于( )
A. B. C. D.
10.如图,二次函数与的图象与过且平行于轴的直线分别交于两点和两点,则的值为( )
A. B. C. D.
二、填空题
11.函数的自变量的取值范围是 .
12.袁隆平同志是我国“共和国勋章”获得者,他的逝世是中国乃至世界的巨大损失,据统计,杂交水稻每亩产的稻谷,可以为中国养活80000000人口,数据80000000用科学记数法表示为 .
13.在一个不透明的盒子中装有4个白球,若干个绿球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是绿球的概率为,则绿球的个数为 个.
14.如图,等边是的内接三角形,若的半径为,则阴影部分的面积为 .
15.虹吸现象描述了液体在两个具有高度差的容器之间,通过充满液体的倒U形管自动流动的过程.如图1,是利用虹吸现象的原理从甲容器向乙容器注水的示意图,已知甲、乙容器完全相同,开始时甲容器液面高.设甲容器中的液面高为(单位:),乙容器中的液面高为(单位:),小明绘制了,关于虹吸时间x(单位:)的函数图象,如图2所示.当甲容器中的液面比乙容器中的液面低时,x的值为 .
三、解答题
16.(1)
(2),再选一个合适的的值代入求值,其中且为整数.
17.已知:如图,点为对角线的中点,过点的直线与,分别相交于点,.
求证:.
18.阿代的数学研学日记
课题:测量旗杆的高度 地点:青岛市山海二十六中学操场 时间:2025月3月2日 昨天上午代兴国老师要带我们去操场测量旗杆的高度,昨天我们小组设计了一个方案,方案如下:小亮拿着标杆垂直于地面放置,我和小聪用卷尺测量标杆、标杆的影长和旗杆的影长,如图1所示,标杆,影长,旗杆的影长,则可求得旗杆的高度为_______. 今天测量时阴天就不能用昨天的方案了,如图2所示,张世昌老师将升旗用绳子拉直,使绳子的底端G刚好触到地面,用仪器测得绳子与地面的夹角为,然后又将绳子拉到一个0.5米高的平台上,拉直绳子使绳子上的H点刚好触到平台,剩余的绳子长度为5米,此时测得绳子与平台的夹角为,利用这些数据能求出旗杆的高度吗?
请你回答阿代的问题.若能,请求出旗杆的高度;若不能,请说明理由.
(参考数据:,,;,,)
19.随着新能源汽车使用的日益普及,各个小区都纷纷完善新能源汽车的配套设施,其中新能源充电桩的建设成为重点工作,某小区也不例外,计划购置单枪、双枪两款新能源充电桩,来满足小区内新能源汽车车主日益增长的充电需求,然而,在购置过程中,面临着不同的价格、数量以及预算限制等问题,就像下面所描述的情况一样.某小区计划购置如图所示的单枪、双枪两款新能源充电桩,购置充电桩的相关信息如表:
单枪充电桩 双枪充电桩
花费:元 花费:元
单价:元/个 单价:元/个
(1)若本次购买单枪充电桩的数量比双枪充电桩的数量多个,求单枪、双枪两款新能源充电桩的单价;
(2)在(1)的条件下,根据居民需求,小区决定再次购进单枪、双枪两款新能源充电桩共个,已知单枪新能源充电桩的单价比上次购买时提高了,双枪新能源充电桩的单价比上次购买时降低了,如果此次加购小区预备支出不超过元,求小区最少需要购买单枪新能源充电桩的数量.
20.2022年10月16日至10月22日,中国共产党第二十次全国代表大会在北京召开.为激励青少年争做党的事业接班人,某市团市委在党史馆组织了“红心永向党”为主题的知识竞赛,依据得分情况将获奖结果分为四个等级:A级为特等奖,B级为一等奖,C级为二等奖,D级为优秀奖.并将统计结果绘制成了如图所示的两幅不完整的统计图.
请根据相关信息解答下列问题:
(1)本次竞赛共有______名选手获奖,扇形统计图中扇形C的圆心角度数是______度;
(2)补全条形统计图;
(3)若该党史馆有一个入口,三个出口.请用树状图或列表法,求参赛选手小丽和小颖由馆内恰好从同一出口走出的概率.
21.中,,点在上,以为半径的圆交于点,交于点.且.
(1)求证:是的切线.
(2)连接交于点,若,求弧的长.
22.如图,在直角三角形中,,,,动点以个单位每秒的速度沿的线路运动,交于点.设运动时间为秒,三角形的周长记为,与的比值记为.
(1)请直接写出、分别关于的函数表达式,并注明的取值范围;
(2)在给定的平面直角坐标系中画出函数,的图象;
(3)请结合函数图象,直接写出时的取值范围.(近似值保留一位小数,误差不超过0.2).
23.如图1,在平面直角坐标系中,抛物线与x轴交于两点,B(点A在B左边),交y轴于C,点是抛物线上一点.
(1)求抛物线的关系式;
(2)在对称轴上找一点M,使的值最小,求点M的坐标;
(3)如图2,抛物线上是否存在点Q,使?若存在,请求出点Q的坐标;若不存在,请说明理由.
《2025年山东省菏泽市东明县中考二模数学试题 》参考答案
1.A
解:∵,
∴最小的数是;
故选:A.
2.B
解:A、是轴对称图形而不是中心对称图形;
B、既是轴对称图形也是中心对称图形;
C、是轴对称图形而不是中心对称图形;
D、是轴对称图形而不是中心对称图形;
故选:B.
3.D
根据合并同类项法则、完全平方公式、积的乘方、单项式乘多项式法则进行计算即可.
解:A、与不是同类项,不能合并,故不符合题意;
B、,故不符合题意;
C、,故不符合题意;
D、,故符合题意;
故选:D.
4.D
解:根据平行线的性质,当点在点左侧时,,
当点在点右侧时,,
故选:D.
5.B
解:由图可得,
第1种如图①有4个氢原子,即,
第2种如图②有6个氢原子,即,
第3种如图③有8个氢原子,即,
,
第10种化合物的分子结构模型中氢原子的个数是:;
故选:B.
6.C
解:由题意得:
,
解得:,
则在数轴上表示为;
故选C.
7.D
解:根据,可得甜果九个用十一文钱,苦果七个用四文钱,
故选:D
8.D
全班共50名学生,班主任制作了50份问卷调查,
所以班主任采用的是全面调查,
故A选项错误;
喜爱娱乐节目的同学所占的百分比最多,因此喜爱娱乐节目的同学最多,
故B选项错误;
喜爱戏曲节目的同学有名,
故C选项错误;
“体育”对应扇形的圆心角为,
故D选项正确.
故选:D.
9.A
连接,,并标注字母如图所示.
根据题意可知,,,,
∵,,
∴∽,
∴,,
∴,
∴,
∴∽,
∴,
∴.
根据勾股定理,得,
∴.
故选:A.
10.A
根据题意:,
解得:,
,
,
根据题意得:,
解得:,
,
,
故选:A.
11.且
解:∵函数有意义,
∴自变量的取值范围为,
解得:且,
故答案为:且.
12.
解:80000000用科学记数法表示为.
故答案为:.
13.12
解:设绿球的个数为x个,则这个不透明的盒子中共装有个球,
根据题意得:,
解得:,
经检验,是方程的解,
∴绿球的个数为12个.
故答案为:12.
14.
解:连接、,连接并延长并于点,如下图,
则.
等边是的内接三角形,
,
,,
,,
,
,
图中阴影部分的面积.
故答案为:.
15./
解:当时,,
∵开始时甲容器液面高,
∴,
又∵时,,
∴设,
将代入得,解得,
∴,
∵甲容器向乙容器注水,始终有,
∴,
∴甲容器中的液面比乙容器中的液面低时,即,
∴,
解得,
故答案为:.
16.(1);(2),时,原式.
(1)解:原式;
(2)解:原式,
要是分式有意义,则,
,原式.
17.详见解析
证明:∵四边形是平行四边形,
∴,,
∴,,
∵点为对角线的中点,
∴,
∴,
∴,
∴,
∴.
18.;旗杆高度可求,为米
(1)解:因为,
所以,
所以,
所以,
所以,
所以;
(2)如图所示,过点H,作于N,
设米,
米,
在中,,
,
在中,,,
,
,
,
解得:,
答:旗杆高度可求,为米.
19.(1)单枪新能源充电桩的价格为1000元/个,双枪新能源充电桩的价格为1500元/个
(2)小区最少需要购买单枪新能源充电桩8个
(1)解:根据题意可得
解得:
经检验,是原方程的解,且符合题意,
(元/个)
答:单枪新能源充电桩的价格为1000元/个,双枪新能源充电桩的价格为1500元/个;
(2)解:单枪新能源充电桩的单价比上次购买时提高了,则现在单枪新能源充电桩的单价为(元/个)
双枪新能源充电桩的单价比上次购买时降低了,则现在双枪新能源充电桩的单价为(元/个)
设再次购进单枪新能源允电社个,则购进双枪新能源允电社个,总花费为元
∵此次加购小区预备支出不超过元
∴
解得
∴的最小值为
答:小区最少需要购买单枪新能源充电桩8个.
20.(1)200,108
(2)见解析
(3)
(1)解:名,
∴本次竞赛共有200名选手获奖,
∴C级的人数为名,
∴扇形统计图中扇形C的圆心角度数是度,
故答案为:200,108;
(2)解:B级的人数为名,
补全统计图如下:
(3)解:设这三个出口分别用E、F、G表示,列表如下:
E F G
E (E,E) (F,E) (G,E)
F (E,F) (F,F) (G,F)
G (E,G) (F,G) (G,G)
由表格可知一共有9种等可能性的结果数,其中参赛选手小丽和小颖由馆内恰好从同一出口走出的结果数有3种,
∴参赛选手小丽和小颖由馆内恰好从同一出口走出的概率.
21.(1)见解析
(2)弧的长为.
(1)证明:连接,
在和中,,
∴,
∴,
∵为的半径,
∴是的切线;
(2)解:∵,
∴,
设的半径为,
在中,,即,
解得,
∴,,,
∴,
∵,
∴,
∴弧的长为.
22.(1),
(2)见解析
(3)当时的取值范围为
(1)解:∵,,,
∴,
∴,,
∵,
∴在中,,,
∴,,
∴,,
∴,;
(2)解:依题意,列表:
0 1 2 5 6
0
10 5 2
描点,连线,函数图象如图所示,
(3)解:由图象得,当时的取值范围为.
23.(1)
(2)
(3)存在,或
(1)将点,代入,
得: ,
解得:
∴抛物线的解析式为 ;
(2)当时,,
∴点,
当时,有,
解得:,,
∴点,
∴抛物线的对称轴为:直线
设直线的关系式为,把点B坐标代入,
得:,解得,,
∴直线的关系式为,
由对称可得,直线与对称轴交点就是所求的点M,
当时,,
∴时,最小;
(3)当Q在下方时,如图,过P作于H,过H作轴, 交y轴于M,过P作于N,
∴,
∵,
∴是等腰直角三角形,
∴,
∴,
∴,
∴,
∴,,
∵,
∵,,
∴,解得 ,
∴,
设直线的解析式为 ,
∴,解得,
∴直线的解析式为 ,
联立直线与抛物线解析式得
,
解得或 ,
∴;
②当Q在上方时, 如图,过P作.于H,过H作.轴, 交y轴于M,过P作于N,
同理得.
综上,存在,点Q的坐标为或
同课章节目录
